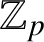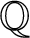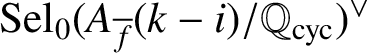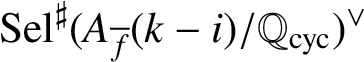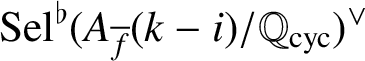1 Introduction
Let p be a fixed odd prime number and f a fixed normalised eigen-cuspform of level N and weight
![]() $k\ge 2$
with
$k\ge 2$
with
![]() $p\nmid N$
. Let K denote the completion of the Hecke field of f at a prime above p and write
$p\nmid N$
. Let K denote the completion of the Hecke field of f at a prime above p and write
![]() $\mathcal {O}$
for its ring of integers. Let
$\mathcal {O}$
for its ring of integers. Let
![]() $V_f$
denote the K-adic
$V_f$
denote the K-adic
![]() $G_{\mathbb {Q}}$
-representation of f defined by Deligne [Reference Deligne8]. We fix a Galois-stable
$G_{\mathbb {Q}}$
-representation of f defined by Deligne [Reference Deligne8]. We fix a Galois-stable
![]() $\mathcal {O}$
-lattice
$\mathcal {O}$
-lattice
![]() $T_f$
inside
$T_f$
inside
![]() $V_f$
and write
$V_f$
and write
![]() $A_f=V_f/T_f$
. We write
$A_f=V_f/T_f$
. We write
![]() ${\overline {f}}$
for the conjugate modular form of f and we write
${\overline {f}}$
for the conjugate modular form of f and we write
![]() $V_{\overline {f}}$
,
$V_{\overline {f}}$
,
![]() $T_{\overline {f}}$
and
$T_{\overline {f}}$
and
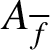 $A_{\overline {f}}$
for the corresponding
$A_{\overline {f}}$
for the corresponding
![]() $G_{\mathbb {Q}}$
-modules attached to
$G_{\mathbb {Q}}$
-modules attached to
![]() ${\overline {f}}$
with
${\overline {f}}$
with
![]() $T_{\overline {f}}$
chosen to be
$T_{\overline {f}}$
chosen to be
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {O}}(T_f,\mathcal {O})(1-k)$
, where
$\operatorname {\mathrm {Hom}}_{\mathcal {O}}(T_f,\mathcal {O})(1-k)$
, where
![]() $M({\kern1.5pt}j)$
denotes the jth Tate twist of a
$M({\kern1.5pt}j)$
denotes the jth Tate twist of a
![]() $G_{\mathbb {Q}}$
-module M.
$G_{\mathbb {Q}}$
-module M.
Let
![]() $\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
be the cyclotomic
$\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
be the cyclotomic
![]() $\mathbb {Z}_p$
-extension of
$\mathbb {Z}_p$
-extension of
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $\Gamma $
denote the Galois group
$\Gamma $
denote the Galois group
![]() $\operatorname {\mathrm {Gal}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}}/\mathbb {Q})$
. The Iwasawa algebra
$\operatorname {\mathrm {Gal}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}}/\mathbb {Q})$
. The Iwasawa algebra
![]() $\Lambda =\mathcal {O}[\![\Gamma ]\!] $
is defined to be
$\Lambda =\mathcal {O}[\![\Gamma ]\!] $
is defined to be
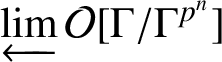 $\varprojlim \mathcal {O}[\Gamma /\Gamma ^{p^n}]$
, where the connecting maps are projections. After fixing a topological generator
$\varprojlim \mathcal {O}[\Gamma /\Gamma ^{p^n}]$
, where the connecting maps are projections. After fixing a topological generator
![]() $\gamma $
of
$\gamma $
of
![]() $\Gamma $
, there is an isomorphism of rings
$\Gamma $
, there is an isomorphism of rings
![]() $\Lambda \cong \mathcal {O}[\![ X]\!] $
sending
$\Lambda \cong \mathcal {O}[\![ X]\!] $
sending
![]() $\gamma $
to
$\gamma $
to
![]() $X+1$
. Given a
$X+1$
. Given a
![]() $\Lambda $
-module M, denote its Pontryagin dual by
$\Lambda $
-module M, denote its Pontryagin dual by
![]() $M^\vee := \operatorname {\mathrm {Hom}}_{\mathcal {O}}( M, K/\mathcal {O})$
. We write
$M^\vee := \operatorname {\mathrm {Hom}}_{\mathcal {O}}( M, K/\mathcal {O})$
. We write
![]() $M^{\iota }$
for the
$M^{\iota }$
for the
![]() $\Lambda $
-module that is M as an
$\Lambda $
-module that is M as an
![]() $\mathcal {O}$
-module equipped with a
$\mathcal {O}$
-module equipped with a
![]() $\Gamma $
-action given by
$\Gamma $
-action given by
![]() $\gamma \cdot _{\iota } m = \gamma ^{-1} m$
. Finally, if
$\gamma \cdot _{\iota } m = \gamma ^{-1} m$
. Finally, if
![]() $F\in \Lambda = \mathcal {O}[\![ X]\!]$
, we write
$F\in \Lambda = \mathcal {O}[\![ X]\!]$
, we write
![]() $F^\iota $
for the power series
$F^\iota $
for the power series
![]() $F({1}/{(1+X)}-1)$
.
$F({1}/{(1+X)}-1)$
.
For
![]() $g=f$
or
$g=f$
or
![]() ${\overline {f}}$
and
${\overline {f}}$
and
![]() $j\in \mathbb {Z}$
, let
$j\in \mathbb {Z}$
, let
![]() $\operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
denote the fine Selmer group of
$\operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
denote the fine Selmer group of
![]() $A_g({\kern1.5pt}j)$
over
$A_g({\kern1.5pt}j)$
over
![]() $\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
(whose definition will be reviewed in Section 2.1). The fine Selmer groups of abelian varieties were first systematically studied by Coates and Sujatha in [Reference Coates and Sujatha7] and a little later by Wuthrich [Reference Wuthrich29]. Various conjectures on the structure of these groups have been formulated and they are still wide open to this date.
$\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
(whose definition will be reviewed in Section 2.1). The fine Selmer groups of abelian varieties were first systematically studied by Coates and Sujatha in [Reference Coates and Sujatha7] and a little later by Wuthrich [Reference Wuthrich29]. Various conjectures on the structure of these groups have been formulated and they are still wide open to this date.
It has been proved by Kato [Reference Kato12] that
![]() $\operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
is a finitely generated torsion
$\operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
is a finitely generated torsion
![]() $\Lambda $
-module. Let
$\Lambda $
-module. Let
![]() $\mathfrak {F}_{g,j}$
denote a choice of characteristic element (that is, a generator of the characteristic ideal
$\mathfrak {F}_{g,j}$
denote a choice of characteristic element (that is, a generator of the characteristic ideal
![]() $\mathrm {Char}_\Lambda \operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
). The main goal of the present article is to study the divisors of
$\mathrm {Char}_\Lambda \operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
). The main goal of the present article is to study the divisors of
![]() $\mathfrak {F}_{f,i}$
and
$\mathfrak {F}_{f,i}$
and
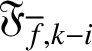 $\mathfrak {F}_{{\overline {f}},k-i}$
for a fixed integer i. These specific twists are considered due to the perfect pairing
$\mathfrak {F}_{{\overline {f}},k-i}$
for a fixed integer i. These specific twists are considered due to the perfect pairing
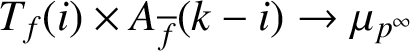 $$ \begin{align*} T_f(i)\times A_{\overline{f}}(k-i)\rightarrow \mu_{p^\infty} \end{align*} $$
$$ \begin{align*} T_f(i)\times A_{\overline{f}}(k-i)\rightarrow \mu_{p^\infty} \end{align*} $$
of
![]() $G_{\mathbb {Q}}$
-modules.
$G_{\mathbb {Q}}$
-modules.
We are able to relate the divisors of
![]() $\mathfrak {F}_{f,i}$
and
$\mathfrak {F}_{f,i}$
and
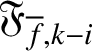 $\mathfrak {F}_{{\overline {f}},k-i}$
to the greatest common divisors of the signed Selmer groups attached to
$\mathfrak {F}_{{\overline {f}},k-i}$
to the greatest common divisors of the signed Selmer groups attached to
![]() ${\overline {f}}(k-i)$
defined in [Reference Lei, Loeffler and Zerbes16, Reference Lei, Loeffler and Zerbes17] by the theory of Wach modules (see Section 2.3, where the definitions of these groups are reviewed). Let us write
${\overline {f}}(k-i)$
defined in [Reference Lei, Loeffler and Zerbes16, Reference Lei, Loeffler and Zerbes17] by the theory of Wach modules (see Section 2.3, where the definitions of these groups are reviewed). Let us write
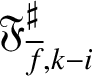 $\mathfrak {F}_{{\overline {f}},k-i}^\sharp $
and
$\mathfrak {F}_{{\overline {f}},k-i}^\sharp $
and
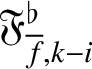 $\mathfrak {F}_{{\overline {f}},k-i}^\flat $
for a choice of characteristic elements of the Pontryagin duals of these signed Selmer groups. Under a mild hypothesis on the local representations at bad primes and a hypothesis on the validity of Kato’s Iwasawa main conjecture for
$\mathfrak {F}_{{\overline {f}},k-i}^\flat $
for a choice of characteristic elements of the Pontryagin duals of these signed Selmer groups. Under a mild hypothesis on the local representations at bad primes and a hypothesis on the validity of Kato’s Iwasawa main conjecture for
![]() ${\overline {f}}(k-i)$
(respectively labelled (H0) and (H-IMC) below), we show that if F is an irreducible element of
${\overline {f}}(k-i)$
(respectively labelled (H0) and (H-IMC) below), we show that if F is an irreducible element of
![]() $\Lambda $
that is outside a certain explicit set of linear factors,
$\Lambda $
that is outside a certain explicit set of linear factors,
![]() $F^\iota \nmid \mathfrak {F}_{f,i}$
and
$F^\iota \nmid \mathfrak {F}_{f,i}$
and
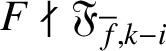 $F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
if and only if
$F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
if and only if
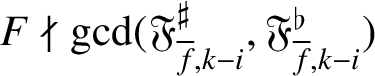 $F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
. (See Theorem 4.4 for the precise statement of this result.)
$F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
. (See Theorem 4.4 for the precise statement of this result.)
In the case where
![]() $T_f$
is the Tate module of an elliptic curve
$T_f$
is the Tate module of an elliptic curve
![]() $E/\mathbb {Q}$
with good supersingular reduction at p, a similar result has been proved in [Reference Lei and Sujatha18]. One of the key ingredients of the proof given in [Reference Lei and Sujatha18] is a link between the fine Selmer group of E over
$E/\mathbb {Q}$
with good supersingular reduction at p, a similar result has been proved in [Reference Lei and Sujatha18]. One of the key ingredients of the proof given in [Reference Lei and Sujatha18] is a link between the fine Selmer group of E over
![]() $\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
and the maximal
$\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
and the maximal
![]() $\Lambda $
-torsion submodule of the Pontryagin dual of the p-primary Selmer group of E over
$\Lambda $
-torsion submodule of the Pontryagin dual of the p-primary Selmer group of E over
![]() $\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
that was proved by Wingberg [Reference Wingberg, Coates, Greenberg, Mazur and Satake28] (see also Matar [Reference Matar19], where an alternative proof is given). In the present paper, we prove Theorem 4.4 by first establishing analogues of Wingberg’s result in the context of modular forms (see Theorems 3.1 and 3.4). Wingberg worked with Selmer groups defined using flat cohomology, whereas Matar worked with Selmer groups defined using Galois cohomology. In the present paper, the latter definition is used. Our proof is very different from the ones employed in both [Reference Matar19] and [Reference Wingberg, Coates, Greenberg, Mazur and Satake28]. We make use of Nekovář’s spectral sequence that seems to give a somewhat simpler and more general proof than the previous proofs available in the literature. We hope that these results may be of independent interest.
$\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
that was proved by Wingberg [Reference Wingberg, Coates, Greenberg, Mazur and Satake28] (see also Matar [Reference Matar19], where an alternative proof is given). In the present paper, we prove Theorem 4.4 by first establishing analogues of Wingberg’s result in the context of modular forms (see Theorems 3.1 and 3.4). Wingberg worked with Selmer groups defined using flat cohomology, whereas Matar worked with Selmer groups defined using Galois cohomology. In the present paper, the latter definition is used. Our proof is very different from the ones employed in both [Reference Matar19] and [Reference Wingberg, Coates, Greenberg, Mazur and Satake28]. We make use of Nekovář’s spectral sequence that seems to give a somewhat simpler and more general proof than the previous proofs available in the literature. We hope that these results may be of independent interest.
2 Definitions of Selmer groups and related objects
2.1 Fine Selmer groups
Let
![]() $L_n$
be the unique subextension of
$L_n$
be the unique subextension of
![]() $\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
such that
$\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
such that
![]() ${[L_n:\mathbb {Q}]=p^n}$
. Given an algebraic extension L of
${[L_n:\mathbb {Q}]=p^n}$
. Given an algebraic extension L of
![]() $\mathbb {Q}$
, we write
$\mathbb {Q}$
, we write
![]() $S(L)$
for the primes of L lying above
$S(L)$
for the primes of L lying above
![]() $pN$
as well as the archimedean primes. We write
$pN$
as well as the archimedean primes. We write
![]() $G_S(L)$
for the Galois group of the maximal algebraic extension of L that is unramified outside
$G_S(L)$
for the Galois group of the maximal algebraic extension of L that is unramified outside
![]() $S(L)$
.
$S(L)$
.
For
![]() $g\in \{f,{\overline {f}}\}$
and
$g\in \{f,{\overline {f}}\}$
and
![]() $j\in \mathbb {Z}$
, we define the fine Selmer group of
$j\in \mathbb {Z}$
, we define the fine Selmer group of
![]() $A_g({\kern1.5pt}j)$
over L to be
$A_g({\kern1.5pt}j)$
over L to be
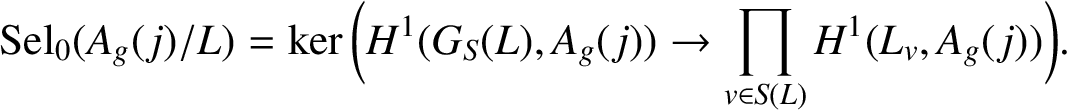 $$ \begin{align*} \operatorname{\mathrm{Sel}}_0(A_g({\kern1.5pt}j)/L)=\ker\bigg(H^1(G_S(L),A_g({\kern1.5pt}j))\rightarrow\prod_{v\in S(L)} H^1(L_v,A_g({\kern1.5pt}j))\bigg). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}_0(A_g({\kern1.5pt}j)/L)=\ker\bigg(H^1(G_S(L),A_g({\kern1.5pt}j))\rightarrow\prod_{v\in S(L)} H^1(L_v,A_g({\kern1.5pt}j))\bigg). \end{align*} $$
Recall that
![]() $\operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
is torsion over
$\operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
is torsion over
![]() $\Lambda $
; we write
$\Lambda $
; we write
![]() $\mathfrak {F}_{g,j}$
for a choice of a generator of the characteristic ideal
$\mathfrak {F}_{g,j}$
for a choice of a generator of the characteristic ideal
![]() $\mathrm {Char}_\Lambda \operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
.
$\mathrm {Char}_\Lambda \operatorname {\mathrm {Sel}}_0(A_g({\kern1.5pt}j)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
.
The classical Selmer group of
![]() $A_g({\kern1.5pt}j)$
over L is defined to be
$A_g({\kern1.5pt}j)$
over L is defined to be
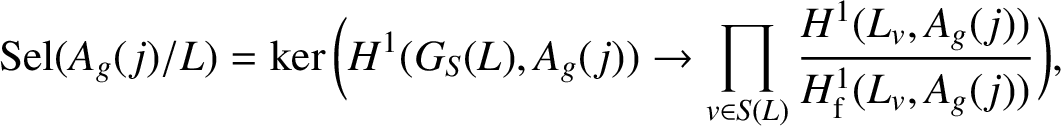 $$ \begin{align*} \operatorname{\mathrm{Sel}}(A_g({\kern1.5pt}j)/L)=\ker\bigg(H^1(G_S(L),A_g({\kern1.5pt}j))\rightarrow\prod_{v\in S(L)} \frac{H^1(L_v,A_g({\kern1.5pt}j))}{H^1_{\mathrm{f}}(L_v,A_g({\kern1.5pt}j))}\bigg), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}(A_g({\kern1.5pt}j)/L)=\ker\bigg(H^1(G_S(L),A_g({\kern1.5pt}j))\rightarrow\prod_{v\in S(L)} \frac{H^1(L_v,A_g({\kern1.5pt}j))}{H^1_{\mathrm{f}}(L_v,A_g({\kern1.5pt}j))}\bigg), \end{align*} $$
where
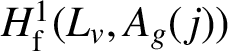 $H^1_{\mathrm {f}}(L_v,A_g({\kern1.5pt}j))$
is defined as in [Reference Bloch, Kato, Cartier, Illusie, Katz, Laumon, Manin and Ribet4, Section 3].
$H^1_{\mathrm {f}}(L_v,A_g({\kern1.5pt}j))$
is defined as in [Reference Bloch, Kato, Cartier, Illusie, Katz, Laumon, Manin and Ribet4, Section 3].
2.2 Wach modules and signed Coleman maps
We recall the definition of signed Coleman maps from [Reference Lei, Loeffler and Zerbes16, Reference Lei, Loeffler and Zerbes17] that generalise those studied in [Reference Kobayashi13, Reference Sprung27] in the context of elliptic curves with supersingular reduction at p. Here, we do not require p to be a nonordinary prime for f. The only requirement is that p is coprime to N, so that the representation
![]() $V_f$
is crystalline at p.
$V_f$
is crystalline at p.
For
![]() $g\in \{f,{\overline {f}}\}$
,
$g\in \{f,{\overline {f}}\}$
,
![]() $j\in \mathbb {Z}$
and
$j\in \mathbb {Z}$
and
![]() $m\in \{1,2\}$
, we shall write
$m\in \{1,2\}$
, we shall write
 $$ \begin{align*} \mathfrak{H}^m_{g,j}=\varprojlim_n H^m(L_n,T_g({\kern1.5pt}j)), \quad \mathbb{H}^m_{g,j}=\varprojlim H^m(L_{n,p},T_g({\kern1.5pt}j)), \end{align*} $$
$$ \begin{align*} \mathfrak{H}^m_{g,j}=\varprojlim_n H^m(L_n,T_g({\kern1.5pt}j)), \quad \mathbb{H}^m_{g,j}=\varprojlim H^m(L_{n,p},T_g({\kern1.5pt}j)), \end{align*} $$
where the connecting maps are corestrictions and we have abused notation by writing p for the unique prime of
![]() $L_n$
above p. We write
$L_n$
above p. We write
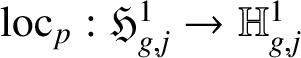 $\mathrm {loc}_p:\mathfrak {H}^1_{g,j}\rightarrow \mathbb {H}^1_{g,j}$
for the localisation map.
$\mathrm {loc}_p:\mathfrak {H}^1_{g,j}\rightarrow \mathbb {H}^1_{g,j}$
for the localisation map.
Let
![]() $T=T_g(k-1)$
, where
$T=T_g(k-1)$
, where
![]() $g\in \{f,{\overline {f}}\}$
. We write
$g\in \{f,{\overline {f}}\}$
. We write
![]() $\mathbb {N}(T)$
for the Wach module of T. (See [Reference Berger3, Section II.1] for the precise definition of
$\mathbb {N}(T)$
for the Wach module of T. (See [Reference Berger3, Section II.1] for the precise definition of
![]() $\mathbb {N}(T)$
.) Roughly speaking,
$\mathbb {N}(T)$
.) Roughly speaking,
![]() $\mathbb {N}(T)$
is a filtered
$\mathbb {N}(T)$
is a filtered
![]() $\varphi $
-module over the ring
$\varphi $
-module over the ring
![]() $\mathcal {O}[\![\pi ]\!]$
, where
$\mathcal {O}[\![\pi ]\!]$
, where
![]() $\pi $
is an element in the ring of Witt vectors of
$\pi $
is an element in the ring of Witt vectors of
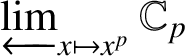 $\varprojlim _{x\mapsto x^p}\mathbb {C}_p$
, given by
$\varprojlim _{x\mapsto x^p}\mathbb {C}_p$
, given by
![]() $[(1, \zeta _p,\zeta _{p^2},\ldots )]-1$
, and
$[(1, \zeta _p,\zeta _{p^2},\ldots )]-1$
, and
![]() $\zeta _{p^n}$
is a primitive
$\zeta _{p^n}$
is a primitive
![]() $p^n$
th root of unity in
$p^n$
th root of unity in
![]() $\mathbb {C}_p$
such that
$\mathbb {C}_p$
such that
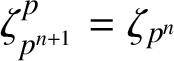 $\zeta _{p^{n+1}}^p=\zeta _{p^n}$
. One may regard
$\zeta _{p^{n+1}}^p=\zeta _{p^n}$
. One may regard
![]() $\pi $
as a formal variable equipped with an action of
$\pi $
as a formal variable equipped with an action of
![]() $\varphi $
and
$\varphi $
and
![]() $\Gamma _0=\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p)$
given by
$\Gamma _0=\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p)$
given by
![]() $\varphi (\pi )=(1+\pi )^p-1$
and
$\varphi (\pi )=(1+\pi )^p-1$
and
![]() ${\sigma (\pi )=(1+\pi )^{\chi _{\operatorname {\mathrm {cyc}}}(\sigma )}-1}$
for
${\sigma (\pi )=(1+\pi )^{\chi _{\operatorname {\mathrm {cyc}}}(\sigma )}-1}$
for
![]() $\sigma \in \Gamma _0$
, where
$\sigma \in \Gamma _0$
, where
![]() $\chi _{\operatorname {\mathrm {cyc}}}$
is the p-adic cyclotomic character. Let
$\chi _{\operatorname {\mathrm {cyc}}}$
is the p-adic cyclotomic character. Let
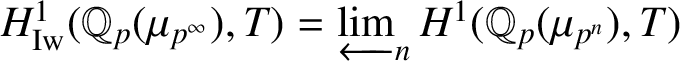 $H^1_{\mathrm {Iw}}(\mathbb {Q}_p(\mu _{p^\infty }),T)=\varprojlim _n H^1(\mathbb {Q}_p(\mu _{p^n}),T)$
, where the connecting maps are corestrictions. Berger proved in [Reference Berger2, Appendix A] that there is an isomorphism of
$H^1_{\mathrm {Iw}}(\mathbb {Q}_p(\mu _{p^\infty }),T)=\varprojlim _n H^1(\mathbb {Q}_p(\mu _{p^n}),T)$
, where the connecting maps are corestrictions. Berger proved in [Reference Berger2, Appendix A] that there is an isomorphism of
![]() $\mathcal {O}[\![\Gamma _0]\!]$
-modules
$\mathcal {O}[\![\Gamma _0]\!]$
-modules
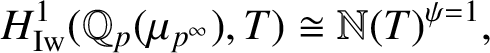 $$ \begin{align*} H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T)\cong \mathbb{N}(T)^{\psi=1}, \end{align*} $$
$$ \begin{align*} H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T)\cong \mathbb{N}(T)^{\psi=1}, \end{align*} $$
where
![]() $\psi $
is a canonical left inverse of
$\psi $
is a canonical left inverse of
![]() $\varphi $
and the superscript
$\varphi $
and the superscript
![]() $\psi =1$
denotes the kernel of
$\psi =1$
denotes the kernel of
![]() $\psi -1$
.
$\psi -1$
.
We recall from [Reference Lei, Loeffler and Zerbes16, Reference Lei, Loeffler and Zerbes17] that for
![]() $\bullet \in \{\sharp ,\flat \}$
, on choosing an appropriate basis of
$\bullet \in \{\sharp ,\flat \}$
, on choosing an appropriate basis of
![]() $\mathbb {N}(T_g(k-1))$
, one can define signed Coleman maps
$\mathbb {N}(T_g(k-1))$
, one can define signed Coleman maps
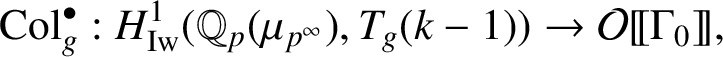 $$ \begin{align*} \mathrm{Col}_g^{\bullet}: H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_g(k-1))\rightarrow \mathcal{O}[\![\Gamma_0]\!], \end{align*} $$
$$ \begin{align*} \mathrm{Col}_g^{\bullet}: H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_g(k-1))\rightarrow \mathcal{O}[\![\Gamma_0]\!], \end{align*} $$
decomposing Perrin-Riou’s big logarithm map defined in [Reference Perrin-Riou22].
We define the twisted Coleman maps
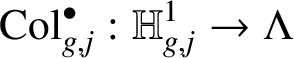 $$ \begin{align*} \mathrm{Col}_{g,j}^{\bullet}:\mathbb{H}^1_{g,j}\rightarrow \Lambda \end{align*} $$
$$ \begin{align*} \mathrm{Col}_{g,j}^{\bullet}:\mathbb{H}^1_{g,j}\rightarrow \Lambda \end{align*} $$
as follows. We have the
![]() $\mathcal {O}$
-isomorphism
$\mathcal {O}$
-isomorphism
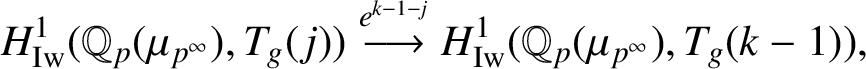 $$ \begin{align*} H^1_{\mathrm{Iw}} (\mathbb{Q}_p(\mu_{p^\infty}),T_g({\kern1.5pt}j))\stackrel{ e^{k-1-j}}{\longrightarrow} H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_g(k-1)), \end{align*} $$
$$ \begin{align*} H^1_{\mathrm{Iw}} (\mathbb{Q}_p(\mu_{p^\infty}),T_g({\kern1.5pt}j))\stackrel{ e^{k-1-j}}{\longrightarrow} H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_g(k-1)), \end{align*} $$
where e is a basis of the
![]() $G_{\mathbb {Q}_p}$
-representation
$G_{\mathbb {Q}_p}$
-representation
![]() $\mathbb {Z}_p(1)$
as given in [Reference Perrin-Riou23, Section A.4]. Let
$\mathbb {Z}_p(1)$
as given in [Reference Perrin-Riou23, Section A.4]. Let
![]() $\operatorname {\mathrm {Tw}}$
be the
$\operatorname {\mathrm {Tw}}$
be the
![]() $\mathcal {O}$
-linear automorphism on
$\mathcal {O}$
-linear automorphism on
![]() $\mathcal {O}[\![\Gamma _0]\!]$
sending
$\mathcal {O}[\![\Gamma _0]\!]$
sending
![]() $\sigma \in \Gamma _0$
to
$\sigma \in \Gamma _0$
to
![]() $\chi _{\operatorname {\mathrm {cyc}}}(\sigma )\sigma $
. We can define a
$\chi _{\operatorname {\mathrm {cyc}}}(\sigma )\sigma $
. We can define a
![]() $\Lambda $
-morphism
$\Lambda $
-morphism
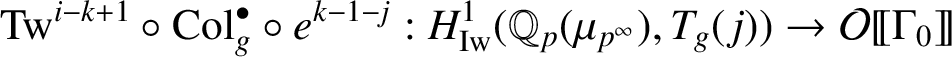 $$ \begin{align*} \operatorname{\mathrm{Tw}}^{i-k+1}\circ\ \mathrm{Col}_g^{\bullet}\circ e^{k-1-j}: H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_g({\kern1.5pt}j))\rightarrow \mathcal{O}[\![\Gamma_0]\!] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Tw}}^{i-k+1}\circ\ \mathrm{Col}_g^{\bullet}\circ e^{k-1-j}: H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_g({\kern1.5pt}j))\rightarrow \mathcal{O}[\![\Gamma_0]\!] \end{align*} $$
and obtain
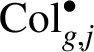 $\mathrm {Col}_{g,j}^{\bullet }$
on taking the trivial isotypic component of
$\mathrm {Col}_{g,j}^{\bullet }$
on taking the trivial isotypic component of
![]() $\Delta :=\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _p)/\mathbb {Q}_p)$
.
$\Delta :=\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _p)/\mathbb {Q}_p)$
.
2.3 Signed Selmer groups and main conjectures
Let
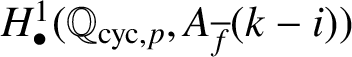 $H_{\bullet }^1(\mathbb {Q}_{\operatorname {\mathrm {cyc}},p},A_{\overline {f}}(k-i))$
denote the orthogonal complement of
$H_{\bullet }^1(\mathbb {Q}_{\operatorname {\mathrm {cyc}},p},A_{\overline {f}}(k-i))$
denote the orthogonal complement of
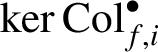 $\ker \mathrm {Col}_{f,i}^{\bullet }$
under the local Tate pairing
$\ker \mathrm {Col}_{f,i}^{\bullet }$
under the local Tate pairing
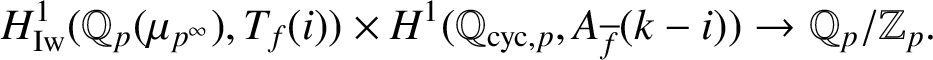 $$ \begin{align*} H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_f(i))\times H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},p},A_{\overline{f}}(k-i))\rightarrow \mathbb{Q}_p/\mathbb{Z}_p. \end{align*} $$
$$ \begin{align*} H^1_{\mathrm{Iw}}(\mathbb{Q}_p(\mu_{p^\infty}),T_f(i))\times H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},p},A_{\overline{f}}(k-i))\rightarrow \mathbb{Q}_p/\mathbb{Z}_p. \end{align*} $$
We define the signed Selmer groups
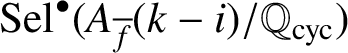 $\operatorname {\mathrm {Sel}}^{\bullet }(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
as
$\operatorname {\mathrm {Sel}}^{\bullet }(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
as
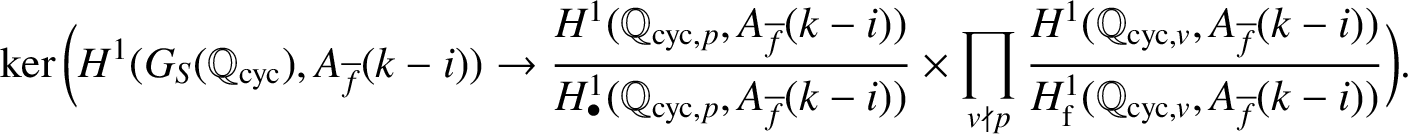 $$ \begin{align*} \ker\bigg(H^1(G_S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}),A_{\overline{f}}(k-i))\rightarrow\frac{ H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},p},A_{\overline{f}}(k-i))}{H_{\bullet}^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},p},A_{\overline{f}}(k-i))}\times \prod_{v\nmid p}\frac{ H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},v},A_{\overline{f}}(k-i))}{H_{\mathrm{f}}^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},v},A_{\overline{f}}(k-i))}\bigg). \end{align*} $$
$$ \begin{align*} \ker\bigg(H^1(G_S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}),A_{\overline{f}}(k-i))\rightarrow\frac{ H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},p},A_{\overline{f}}(k-i))}{H_{\bullet}^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},p},A_{\overline{f}}(k-i))}\times \prod_{v\nmid p}\frac{ H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},v},A_{\overline{f}}(k-i))}{H_{\mathrm{f}}^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}},v},A_{\overline{f}}(k-i))}\bigg). \end{align*} $$
Note that when
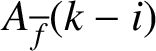 $A_{\overline {f}}(k-i)$
is given by
$A_{\overline {f}}(k-i)$
is given by
![]() $E[p^\infty ]$
for some elliptic curve
$E[p^\infty ]$
for some elliptic curve
![]() $E/\mathbb {Q}$
with good supersingular reduction at p or when
$E/\mathbb {Q}$
with good supersingular reduction at p or when
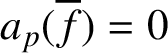 $a_p({\overline {f}})=0$
, one may choose an appropriate basis of the Wach module so that these Selmer groups coincide with the ones studied in [Reference Kobayashi13, Reference Lei14, Reference Sprung27] (see [Reference Lei, Loeffler and Zerbes16, Sections 5.2–5.4]).
$a_p({\overline {f}})=0$
, one may choose an appropriate basis of the Wach module so that these Selmer groups coincide with the ones studied in [Reference Kobayashi13, Reference Lei14, Reference Sprung27] (see [Reference Lei, Loeffler and Zerbes16, Sections 5.2–5.4]).
Let
![]() $\mathbf {z}_{f,i}$
be Kato’s zeta element inside
$\mathbf {z}_{f,i}$
be Kato’s zeta element inside
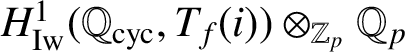 $H^1_{\mathrm {Iw}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}},T_f(i))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
as defined in [Reference Kato12]. It is conjectured that
$H^1_{\mathrm {Iw}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}},T_f(i))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
as defined in [Reference Kato12]. It is conjectured that
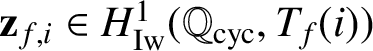 $\mathbf {z}_{f,i}\in H^1_{\mathrm {Iw}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}},T_f(i))$
(see [Reference Kato12, Conjecture 12.10]). Assuming this (which we shall do for the rest of the article), recall from [Reference Lei, Loeffler and Zerbes16, Equation (61)] the Poitou–Tate exact sequence
$\mathbf {z}_{f,i}\in H^1_{\mathrm {Iw}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}},T_f(i))$
(see [Reference Kato12, Conjecture 12.10]). Assuming this (which we shall do for the rest of the article), recall from [Reference Lei, Loeffler and Zerbes16, Equation (61)] the Poitou–Tate exact sequence
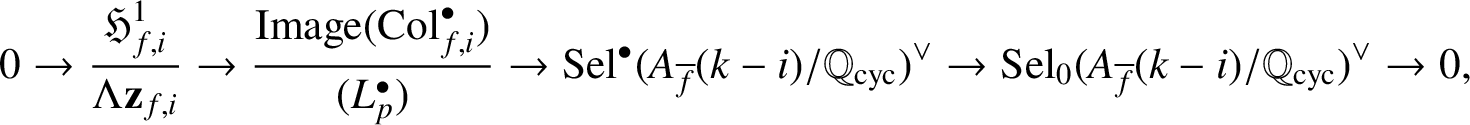 $$ \begin{align} 0\rightarrow\frac{\mathfrak{H}^1_{f,i}}{\Lambda \mathbf{z}_{f,i}}\rightarrow\frac{\mathrm{Image}(\mathrm{Col}_{f,i}^{\bullet})}{(L_p^{\bullet})}\rightarrow \operatorname{\mathrm{Sel}}^{\bullet}(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\rightarrow 0, \end{align} $$
$$ \begin{align} 0\rightarrow\frac{\mathfrak{H}^1_{f,i}}{\Lambda \mathbf{z}_{f,i}}\rightarrow\frac{\mathrm{Image}(\mathrm{Col}_{f,i}^{\bullet})}{(L_p^{\bullet})}\rightarrow \operatorname{\mathrm{Sel}}^{\bullet}(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\rightarrow 0, \end{align} $$
where
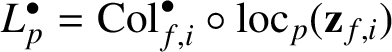 $L_p^{\bullet }=\mathrm {Col}_{f,i}^{\bullet }\circ \mathrm {loc}_p(\mathbf {z}_{f,i})$
is the signed p-adic L-function associated to
$L_p^{\bullet }=\mathrm {Col}_{f,i}^{\bullet }\circ \mathrm {loc}_p(\mathbf {z}_{f,i})$
is the signed p-adic L-function associated to
![]() ${\overline {f}}(k-i)$
. If
${\overline {f}}(k-i)$
. If
![]() $L_p^{\bullet }\ne 0$
, then
$L_p^{\bullet }\ne 0$
, then
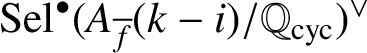 $\operatorname {\mathrm {Sel}}^{\bullet }(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
is a finitely generated torsion
$\operatorname {\mathrm {Sel}}^{\bullet }(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
is a finitely generated torsion
![]() $\Lambda $
-module. We write
$\Lambda $
-module. We write
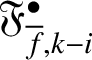 $\mathfrak {F}_{{\overline {f}},k-i}^{\bullet }$
for a characteristic element of this module.
$\mathfrak {F}_{{\overline {f}},k-i}^{\bullet }$
for a characteristic element of this module.
Kato [Reference Kato12] proved that the first and fourth terms of (2.1) are
![]() $\Lambda $
-torsion. He further formulated the Iwasawa main conjecture:
$\Lambda $
-torsion. He further formulated the Iwasawa main conjecture:
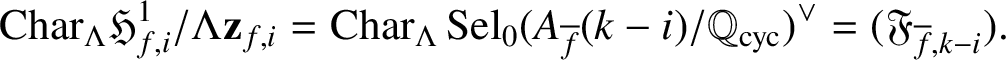 $$ \begin{align} \mathrm{Char}_\Lambda\mathfrak{H}^1_{f,i}/\Lambda \mathbf{z}_{f,i}=\mathrm{Char}_\Lambda\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee=(\mathfrak{F}_{{\overline{f}},k-i}). \end{align} $$
$$ \begin{align} \mathrm{Char}_\Lambda\mathfrak{H}^1_{f,i}/\Lambda \mathbf{z}_{f,i}=\mathrm{Char}_\Lambda\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee=(\mathfrak{F}_{{\overline{f}},k-i}). \end{align} $$
It follows from (2.1) that this is equivalent to
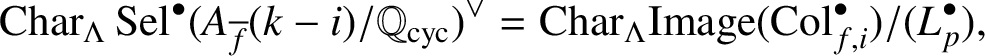 $$ \begin{align} \mathrm{Char}_\Lambda\operatorname{\mathrm{Sel}}^{\bullet}(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee=\mathrm{Char}_\Lambda\mathrm{Image}(\mathrm{Col}_{f,i}^{\bullet})/(L_p^{\bullet}), \end{align} $$
$$ \begin{align} \mathrm{Char}_\Lambda\operatorname{\mathrm{Sel}}^{\bullet}(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee=\mathrm{Char}_\Lambda\mathrm{Image}(\mathrm{Col}_{f,i}^{\bullet})/(L_p^{\bullet}), \end{align} $$
provided that
![]() $L_p^{\bullet }\ne 0$
.
$L_p^{\bullet }\ne 0$
.
For the rest of the article, we shall assume that the following hypothesis holds.
(H-IMC) Kato’s Iwasawa main conjecture (2.2) holds and both
![]() $L_p^\sharp $
and
$L_p^\sharp $
and
![]() $L_p^\flat $
are nonzero.
$L_p^\flat $
are nonzero.
Remark 2.1. We say a few words on the hypothesis (H-IMC). In his seminal work [Reference Kato12], Kato established that the inclusion ‘
![]() $\subseteq $
’ in (2.2) holds after tensoring by
$\subseteq $
’ in (2.2) holds after tensoring by
![]() $\mathbb {Q}_p$
under the assumption that the image of the representation
$\mathbb {Q}_p$
under the assumption that the image of the representation
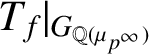 $T_f|_{G_{\mathbb {Q}(\mu _{p^\infty })}}$
contains a copy of
$T_f|_{G_{\mathbb {Q}(\mu _{p^\infty })}}$
contains a copy of
![]() $\mathrm {SL}_2(\mathbb {Z}_p)$
, provided that certain local terms vanish (see, in particular, [Reference Kato12, Theorem 12.5(4)]). Note that in [Reference Kato12, Conjecture 12.10], Kato’s main conjecture is formulated in terms of étale cohomology groups. Kobayashi and Kurihara showed that it can be recast in terms of Galois cohomology groups and fine Selmer groups (see, for example, [Reference Kobayashi13, Proposition 7.1]). The reverse inclusion of (2.2) has been established in the monumental work of Skinner and Urban [Reference Skinner and Urban26] for a p-ordinary modular form (under certain hypotheses; see [Reference Skinner and Urban26, Theorem 1]). In the nonordinary form, there have been several recent breakthroughs in this reverse direction (see [Reference Castella, Çiperiani, Skinner and Sprung5, Reference Castella, Liu and Wan6, Reference Fouquet and Wan9]). Finally, the work [Reference Lei, Loeffler and Zerbes16] has supplied many sufficient conditions for the nonvanishing of
$\mathrm {SL}_2(\mathbb {Z}_p)$
, provided that certain local terms vanish (see, in particular, [Reference Kato12, Theorem 12.5(4)]). Note that in [Reference Kato12, Conjecture 12.10], Kato’s main conjecture is formulated in terms of étale cohomology groups. Kobayashi and Kurihara showed that it can be recast in terms of Galois cohomology groups and fine Selmer groups (see, for example, [Reference Kobayashi13, Proposition 7.1]). The reverse inclusion of (2.2) has been established in the monumental work of Skinner and Urban [Reference Skinner and Urban26] for a p-ordinary modular form (under certain hypotheses; see [Reference Skinner and Urban26, Theorem 1]). In the nonordinary form, there have been several recent breakthroughs in this reverse direction (see [Reference Castella, Çiperiani, Skinner and Sprung5, Reference Castella, Liu and Wan6, Reference Fouquet and Wan9]). Finally, the work [Reference Lei, Loeffler and Zerbes16] has supplied many sufficient conditions for the nonvanishing of
![]() $L_p^\sharp $
and
$L_p^\sharp $
and
![]() $L_p^\flat $
(see [Reference Lei, Loeffler and Zerbes16, Corollary 3.29 and Proposition 3.39]). In view of these developments, it seems reasonable to assume hypothesis (H-IMC); our main results rely on it.
$L_p^\flat $
(see [Reference Lei, Loeffler and Zerbes16, Corollary 3.29 and Proposition 3.39]). In view of these developments, it seems reasonable to assume hypothesis (H-IMC); our main results rely on it.
2.4 Images of signed Coleman maps
We review an explicit description of the images of these Coleman maps. Recall that
![]() $\gamma $
is a fixed topological generator of
$\gamma $
is a fixed topological generator of
![]() $\Gamma $
giving the identification
$\Gamma $
giving the identification
![]() $\Lambda =\mathcal {O}[\![ X]\!]$
via
$\Lambda =\mathcal {O}[\![ X]\!]$
via
![]() $X=\gamma -1$
. Let
$X=\gamma -1$
. Let
![]() $u=\chi _{\operatorname {\mathrm {cyc}}}(\gamma )$
. From [Reference Lei, Loeffler and Zerbes17, Section 5A], if
$u=\chi _{\operatorname {\mathrm {cyc}}}(\gamma )$
. From [Reference Lei, Loeffler and Zerbes17, Section 5A], if
![]() $\eta $
is a character on
$\eta $
is a character on
![]() $\Delta $
, then there exist constants
$\Delta $
, then there exist constants
![]() $c_{\eta ,j}\in K$
such that
$c_{\eta ,j}\in K$
such that
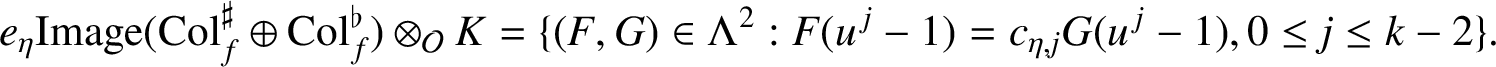 $$ \begin{align*} e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat)\otimes_{\mathcal{O}} K=\{(F,G)\in \Lambda^2:F(u^{{\kern1.5pt}j}-1)=c_{\eta,j}G(u^{{\kern1.5pt}j}-1),0\le j\le k-2\}. \end{align*} $$
$$ \begin{align*} e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat)\otimes_{\mathcal{O}} K=\{(F,G)\in \Lambda^2:F(u^{{\kern1.5pt}j}-1)=c_{\eta,j}G(u^{{\kern1.5pt}j}-1),0\le j\le k-2\}. \end{align*} $$
(In [Reference Lei, Loeffler and Zerbes17], it is assumed that f is nonordinary at p, meaning that
![]() $a_p(f)$
is a nonunit in
$a_p(f)$
is a nonunit in
![]() $\mathcal {O}$
. But the same calculations still apply to the ordinary case. See [Reference Lei, Loeffler and Zerbes17, Remark 1.10].) In particular, this tells us that there is an isomorphism of
$\mathcal {O}$
. But the same calculations still apply to the ordinary case. See [Reference Lei, Loeffler and Zerbes17, Remark 1.10].) In particular, this tells us that there is an isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
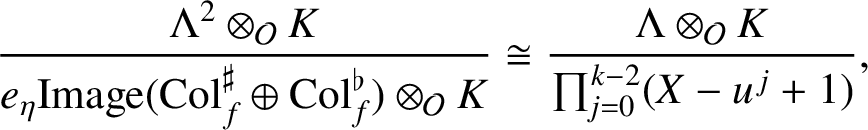 $$ \begin{align*}\frac{\Lambda^2\otimes_{\mathcal{O}} K}{ e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat)\otimes_{\mathcal{O}} K}\cong \frac{\Lambda\otimes_{\mathcal{O}} K}{\prod_{j=0}^{k-2}(X-u^{{\kern1.5pt}j}+1)}, \end{align*} $$
$$ \begin{align*}\frac{\Lambda^2\otimes_{\mathcal{O}} K}{ e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat)\otimes_{\mathcal{O}} K}\cong \frac{\Lambda\otimes_{\mathcal{O}} K}{\prod_{j=0}^{k-2}(X-u^{{\kern1.5pt}j}+1)}, \end{align*} $$
where
![]() $e_\eta $
denotes the idempotent attached to
$e_\eta $
denotes the idempotent attached to
![]() $\eta $
.
$\eta $
.
Lemma 2.2. There is a pseudo-isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
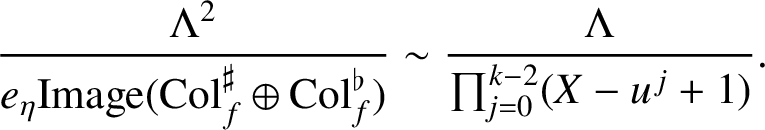 $$ \begin{align*} \frac{\Lambda^2}{e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat)}\sim \frac{\Lambda}{\prod_{j=0}^{k-2}(X-u^{{\kern1.5pt}j}+1)}. \end{align*} $$
$$ \begin{align*} \frac{\Lambda^2}{e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat)}\sim \frac{\Lambda}{\prod_{j=0}^{k-2}(X-u^{{\kern1.5pt}j}+1)}. \end{align*} $$
Proof. It is enough to show that the
![]() $\mu $
-invariant of the quotient on the left-hand side vanishes. For simplicity, let us write
$\mu $
-invariant of the quotient on the left-hand side vanishes. For simplicity, let us write
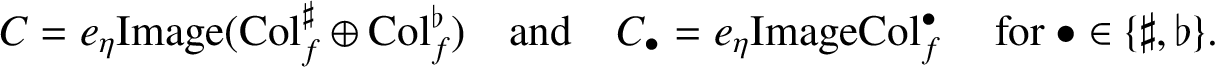 $$ \begin{align*} C=e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat) \quad\text{and}\quad C_{\bullet}=e_\eta\mathrm{Image}\mathrm{Col}_f^{\bullet} \quad\mbox{ for } \bullet\in\{\sharp,\flat\}. \end{align*} $$
$$ \begin{align*} C=e_\eta\mathrm{Image}(\mathrm{Col}_{f}^\sharp\oplus \mathrm{Col}_f^\flat) \quad\text{and}\quad C_{\bullet}=e_\eta\mathrm{Image}\mathrm{Col}_f^{\bullet} \quad\mbox{ for } \bullet\in\{\sharp,\flat\}. \end{align*} $$
Consider the tautological short exact sequence
![]() $ 0\rightarrow C\rightarrow \Lambda ^2\rightarrow \Lambda ^2/C\rightarrow 0. $
This gives the exact sequence
$ 0\rightarrow C\rightarrow \Lambda ^2\rightarrow \Lambda ^2/C\rightarrow 0. $
This gives the exact sequence
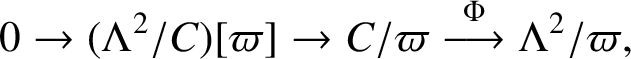 $$ \begin{align*} 0\rightarrow(\Lambda^2/C)[\varpi]\rightarrow C/\varpi\stackrel{\Phi}{\longrightarrow} \Lambda^2/\varpi, \end{align*} $$
$$ \begin{align*} 0\rightarrow(\Lambda^2/C)[\varpi]\rightarrow C/\varpi\stackrel{\Phi}{\longrightarrow} \Lambda^2/\varpi, \end{align*} $$
where
![]() $\varpi $
is a fixed uniformiser of
$\varpi $
is a fixed uniformiser of
![]() $\mathcal {O}$
. Similarly, we have the exact sequences
$\mathcal {O}$
. Similarly, we have the exact sequences
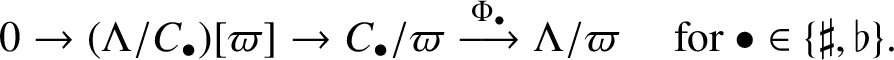 $$ \begin{align*} 0\rightarrow(\Lambda/C_{\bullet})[\varpi]\rightarrow C_{\bullet}/\varpi\stackrel{\Phi_{\bullet}}{\longrightarrow} \Lambda/\varpi \quad\mbox{ for } \bullet\in\{\sharp,\flat\}. \end{align*} $$
$$ \begin{align*} 0\rightarrow(\Lambda/C_{\bullet})[\varpi]\rightarrow C_{\bullet}/\varpi\stackrel{\Phi_{\bullet}}{\longrightarrow} \Lambda/\varpi \quad\mbox{ for } \bullet\in\{\sharp,\flat\}. \end{align*} $$
Recall from [Reference Lei, Loeffler and Zerbes17, Theorem 5.10] that the
![]() $\mu $
-invariants of
$\mu $
-invariants of
![]() $\Lambda /C_{\bullet }$
are zero. Therefore,
$\Lambda /C_{\bullet }$
are zero. Therefore,
![]() $\ker \Phi _{\bullet }=(\Lambda /C_{\bullet })[\varpi ]$
is finite for both choices of
$\ker \Phi _{\bullet }=(\Lambda /C_{\bullet })[\varpi ]$
is finite for both choices of
![]() $\bullet $
. Note that
$\bullet $
. Note that
![]() $C\subset C_\sharp \oplus C_\flat $
and
$C\subset C_\sharp \oplus C_\flat $
and
![]() $\Phi =(\Phi _\sharp \oplus \Phi _\flat )|_{C/\varpi }$
by definition, which implies that
$\Phi =(\Phi _\sharp \oplus \Phi _\flat )|_{C/\varpi }$
by definition, which implies that
Hence,
![]() $\ker \Phi =(\Lambda ^2/C)[\varpi ]$
is finite. In particular, the
$\ker \Phi =(\Lambda ^2/C)[\varpi ]$
is finite. In particular, the
![]() $\mu $
-invariant of
$\mu $
-invariant of
![]() $\Lambda ^2/C$
is zero, which finishes the proof of the lemma.
$\Lambda ^2/C$
is zero, which finishes the proof of the lemma.
Remark 2.3. In the case where
![]() $T_f$
is the p-adic Tate module of an elliptic curve with good supersingular reduction at p, we can in fact describe the set C explicitly. See [Reference Lei and Lim15, Proposition 2.2].
$T_f$
is the p-adic Tate module of an elliptic curve with good supersingular reduction at p, we can in fact describe the set C explicitly. See [Reference Lei and Lim15, Proposition 2.2].
It follows from Lemma 2.2 that there is an exact sequence
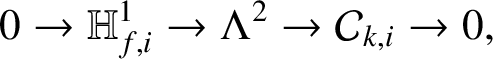 $$ \begin{align} 0\rightarrow \mathbb{H}^1_{f,i}\rightarrow \Lambda^2\rightarrow \mathcal{C}_{k,i}\rightarrow 0, \end{align} $$
$$ \begin{align} 0\rightarrow \mathbb{H}^1_{f,i}\rightarrow \Lambda^2\rightarrow \mathcal{C}_{k,i}\rightarrow 0, \end{align} $$
where the first map is given by
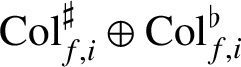 $\mathrm {Col}_{f,i}^\sharp \oplus \mathrm {Col}_{f,i}^\flat $
and
$\mathrm {Col}_{f,i}^\sharp \oplus \mathrm {Col}_{f,i}^\flat $
and
![]() $\mathcal {C}_{k,i}$
is a
$\mathcal {C}_{k,i}$
is a
![]() $\Lambda $
-module, which is pseudo-isomorphic to
$\Lambda $
-module, which is pseudo-isomorphic to
![]() $\Lambda /\eta _{k,i}$
, with
$\Lambda /\eta _{k,i}$
, with
![]() $\eta _{k,i}$
being the image of
$\eta _{k,i}$
being the image of
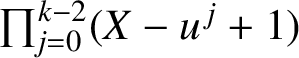 $\prod _{j=0}^{k-2}(X-u^{{\kern1.5pt}j}+1)$
under the twisting map
$\prod _{j=0}^{k-2}(X-u^{{\kern1.5pt}j}+1)$
under the twisting map
![]() $\operatorname {\mathrm {Tw}}^{i-k+1}$
.
$\operatorname {\mathrm {Tw}}^{i-k+1}$
.
3 A generalisation of a result of Wingberg
Let
![]() $\mathcal {A}$
be an abelian variety over
$\mathcal {A}$
be an abelian variety over
![]() $\mathbb {Q}$
with supersingular reduction at p. Wingberg proved that there is a pseudo-isomorphism of
$\mathbb {Q}$
with supersingular reduction at p. Wingberg proved that there is a pseudo-isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
where
![]() $\mathcal {A}^t$
is the dual abelian variety of
$\mathcal {A}^t$
is the dual abelian variety of
![]() $\mathcal {A}$
(see [Reference Wingberg, Coates, Greenberg, Mazur and Satake28, Corollary 2.5]). Here,
$\mathcal {A}$
(see [Reference Wingberg, Coates, Greenberg, Mazur and Satake28, Corollary 2.5]). Here,
![]() $M_{\Lambda -\mathrm {tor}}$
denotes the maximal torsion submodule of a
$M_{\Lambda -\mathrm {tor}}$
denotes the maximal torsion submodule of a
![]() $\Lambda $
-module M,
$\Lambda $
-module M,
![]() $\operatorname {\mathrm {Sel}}(\mathcal {A}[p^\infty ]/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
is the p-primary Selmer group of
$\operatorname {\mathrm {Sel}}(\mathcal {A}[p^\infty ]/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
is the p-primary Selmer group of
![]() $\mathcal {A}$
over
$\mathcal {A}$
over
![]() $\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
and
$\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
and
![]() $\operatorname {\mathrm {Sel}}_0(\mathcal {A}^t[p^\infty ]/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
is the p-primary fine Selmer group of
$\operatorname {\mathrm {Sel}}_0(\mathcal {A}^t[p^\infty ]/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
is the p-primary fine Selmer group of
![]() $\mathcal {A}^t$
over
$\mathcal {A}^t$
over
![]() $\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
defined in a similar manner to the fine Selmer groups for
$\mathbb {Q}_{\operatorname {\mathrm {cyc}}}$
defined in a similar manner to the fine Selmer groups for
![]() $A_g({\kern1.5pt}j)$
in Section 2.1 above. We prove the following analogue of Wingberg’s result in the context of modular forms.
$A_g({\kern1.5pt}j)$
in Section 2.1 above. We prove the following analogue of Wingberg’s result in the context of modular forms.
Theorem 3.1. We have a pseudo-isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
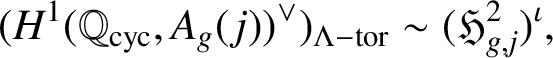 $$ \begin{align*} (H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_g({\kern1.5pt}j))^\vee)_{\Lambda-\mathrm{tor}}\sim (\mathfrak{H}^2_{g,j})^\iota, \end{align*} $$
$$ \begin{align*} (H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_g({\kern1.5pt}j))^\vee)_{\Lambda-\mathrm{tor}}\sim (\mathfrak{H}^2_{g,j})^\iota, \end{align*} $$
where
![]() $g\in \{f,{\overline {f}}\}$
and
$g\in \{f,{\overline {f}}\}$
and
![]() $j\in \mathbb {Z}$
.
$j\in \mathbb {Z}$
.
Proof. From the low-degree terms of Nekovář’s spectral sequence (see [Reference Nekovář20, Lemma 9.1.5]),
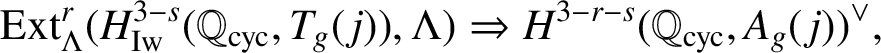 $$ \begin{align*} \operatorname{\mathrm{Ext}}_{\Lambda}^{r}( H^{3-s}_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda)\Rightarrow H^{3-r-s}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_g({\kern1.5pt}j))^\vee, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ext}}_{\Lambda}^{r}( H^{3-s}_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda)\Rightarrow H^{3-r-s}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_g({\kern1.5pt}j))^\vee, \end{align*} $$
we obtain the exact sequence of
![]() $\Lambda $
-modules
$\Lambda $
-modules
 $$ \begin{align*} 0 \longrightarrow \operatorname{\mathrm{Ext}}_{\Lambda}^{1}( H^2_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda)\longrightarrow H^{1}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_g({\kern1.5pt}j))^\vee \longrightarrow \operatorname{\mathrm{Hom}}_{\Lambda}( H^1_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda).\end{align*} $$
$$ \begin{align*} 0 \longrightarrow \operatorname{\mathrm{Ext}}_{\Lambda}^{1}( H^2_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda)\longrightarrow H^{1}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_g({\kern1.5pt}j))^\vee \longrightarrow \operatorname{\mathrm{Hom}}_{\Lambda}( H^1_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda).\end{align*} $$
Since
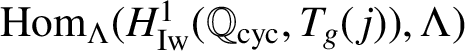 $\operatorname {\mathrm {Hom}}_{\Lambda }( H^1_{\operatorname {\mathrm {Iw}}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}}, T_g({\kern1.5pt}j)), \Lambda )$
is a reflexive
$\operatorname {\mathrm {Hom}}_{\Lambda }( H^1_{\operatorname {\mathrm {Iw}}}(\mathbb {Q}_{\operatorname {\mathrm {cyc}}}, T_g({\kern1.5pt}j)), \Lambda )$
is a reflexive
![]() $\Lambda $
-module by [Reference Neukirch, Schmidt and Wingberg21, Corollary 5.1.3], it is
$\Lambda $
-module by [Reference Neukirch, Schmidt and Wingberg21, Corollary 5.1.3], it is
![]() $\Lambda $
-torsion-free. Hence, it follows from the exact sequence that there is an isomorphism
$\Lambda $
-torsion-free. Hence, it follows from the exact sequence that there is an isomorphism
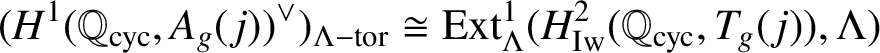 $$ \begin{align*} (H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_g({\kern1.5pt}j))^\vee)_{\Lambda-\mathrm{tor}}\cong \operatorname{\mathrm{Ext}}_{\Lambda}^{1}( H^2_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda) \end{align*} $$
$$ \begin{align*} (H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_g({\kern1.5pt}j))^\vee)_{\Lambda-\mathrm{tor}}\cong \operatorname{\mathrm{Ext}}_{\Lambda}^{1}( H^2_{\operatorname{\mathrm{Iw}}}(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, T_g({\kern1.5pt}j)), \Lambda) \end{align*} $$
of
![]() $\Lambda $
-modules. By [Reference Neukirch, Schmidt and Wingberg21, Proposition 5.5.13], the latter is pseudo-isomorphic to
$\Lambda $
-modules. By [Reference Neukirch, Schmidt and Wingberg21, Proposition 5.5.13], the latter is pseudo-isomorphic to
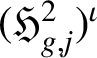 $(\mathfrak {H}^2_{g,j})^\iota $
, which concludes the proof of the theorem.
$(\mathfrak {H}^2_{g,j})^\iota $
, which concludes the proof of the theorem.
When f is nonordinary at p, we shall establish a direct analogue of Wingberg’s theorem on the level of Selmer groups under the following hypothesis on the local representation
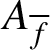 $A_{\overline {f}}$
(see Theorem 3.4 below).
$A_{\overline {f}}$
(see Theorem 3.4 below).
(H0) For all
![]() $v\in S(\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
, the group
$v\in S(\mathbb {Q}_{\operatorname {\mathrm {cyc}}})$
, the group
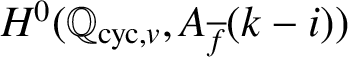 $H^0(\mathbb {Q}_{\operatorname {\mathrm {cyc}},v},A_{\overline {f}}(k-i))$
is finite.
$H^0(\mathbb {Q}_{\operatorname {\mathrm {cyc}},v},A_{\overline {f}}(k-i))$
is finite.
Remark 3.2. Note that when
![]() $v \mid p$
, the group
$v \mid p$
, the group
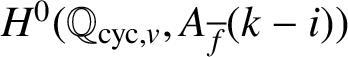 $H^0(\mathbb {Q}_{\operatorname {\mathrm {cyc}},v},A_{\overline {f}}(k-i))$
is always finite by [Reference Hatley, Kundu, Lei and Ray10, Lemma 3.3]. See also [Reference Hatley, Kundu, Lei and Ray10, Section 5], where sufficient conditions and explicit examples of the finiteness of
$H^0(\mathbb {Q}_{\operatorname {\mathrm {cyc}},v},A_{\overline {f}}(k-i))$
is always finite by [Reference Hatley, Kundu, Lei and Ray10, Lemma 3.3]. See also [Reference Hatley, Kundu, Lei and Ray10, Section 5], where sufficient conditions and explicit examples of the finiteness of
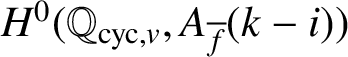 $H^0(\mathbb {Q}_{\operatorname {\mathrm {cyc}},v},A_{\overline {f}}(k-i))$
for
$H^0(\mathbb {Q}_{\operatorname {\mathrm {cyc}},v},A_{\overline {f}}(k-i))$
for
![]() $v \mid N$
are studied.
$v \mid N$
are studied.
Lemma 3.3. Under (H0), we have a pseudo-isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
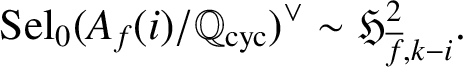 $$ \begin{align*} \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\sim \mathfrak{H}^2_{{\overline{f}},k-i}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\sim \mathfrak{H}^2_{{\overline{f}},k-i}. \end{align*} $$
Proof. Let
![]() $n\ge 0$
be an integer. By the Poitou–Tate exact sequence (see, for example, [Reference Perrin-Riou23, Section A.3.1]), we have the exact sequence
$n\ge 0$
be an integer. By the Poitou–Tate exact sequence (see, for example, [Reference Perrin-Riou23, Section A.3.1]), we have the exact sequence
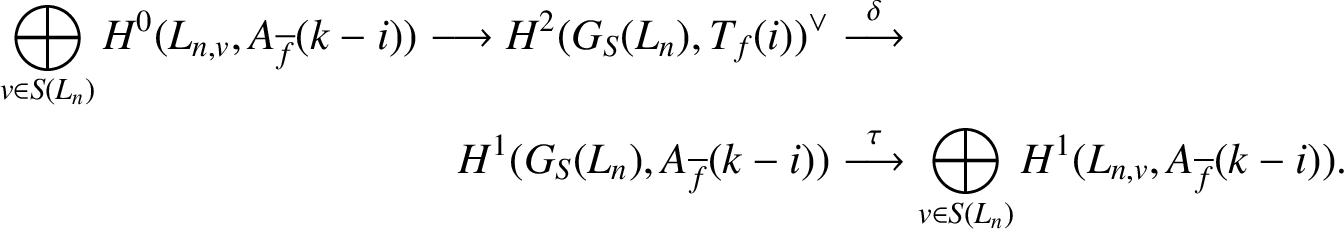 $$ \begin{align*} \bigoplus_{v \in S(L_n)}H^0(L_{n,v}, A_{\overline{f}}(k-i))\longrightarrow H^2(G_S(L_n), T_f(i))^{\vee}&\stackrel{\delta}{\longrightarrow} \\ H^1(G_S(L_n), A_{\overline{f}}(k-i))& \stackrel{\tau}{\longrightarrow} \bigoplus_{v \in S(L_n)}H^1(L_{n,v},A_{\overline{f}}(k-i)). \end{align*} $$
$$ \begin{align*} \bigoplus_{v \in S(L_n)}H^0(L_{n,v}, A_{\overline{f}}(k-i))\longrightarrow H^2(G_S(L_n), T_f(i))^{\vee}&\stackrel{\delta}{\longrightarrow} \\ H^1(G_S(L_n), A_{\overline{f}}(k-i))& \stackrel{\tau}{\longrightarrow} \bigoplus_{v \in S(L_n)}H^1(L_{n,v},A_{\overline{f}}(k-i)). \end{align*} $$
By definition,
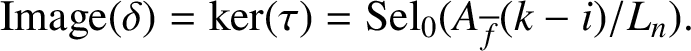 $$ \begin{align*} \mathrm{Image}(\delta)=\ker(\tau)=\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/L_n). \end{align*} $$
$$ \begin{align*} \mathrm{Image}(\delta)=\ker(\tau)=\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/L_n). \end{align*} $$
This gives the exact sequence
 $$ \begin{align*} \bigoplus_{v \in S(L_n)}H^0(L_{n,v}, A_{\overline{f}}(k-i)) \longrightarrow H^2(G_S(L_n), T_f(i)) ^{\vee} \longrightarrow \operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/L_n) \longrightarrow 0.\end{align*} $$
$$ \begin{align*} \bigoplus_{v \in S(L_n)}H^0(L_{n,v}, A_{\overline{f}}(k-i)) \longrightarrow H^2(G_S(L_n), T_f(i)) ^{\vee} \longrightarrow \operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/L_n) \longrightarrow 0.\end{align*} $$
By the local Tate duality,
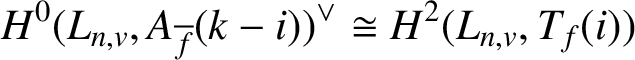 $$ \begin{align*}H^0(L_{n,v}, A_{\overline{f}}(k-i))^{\vee} \cong H^2(L_{n,v}, T_f(i))\end{align*} $$
$$ \begin{align*}H^0(L_{n,v}, A_{\overline{f}}(k-i))^{\vee} \cong H^2(L_{n,v}, T_f(i))\end{align*} $$
for all
![]() $v\in S$
. Thus, after taking Pontryagin duals and inverse limits,
$v\in S$
. Thus, after taking Pontryagin duals and inverse limits,
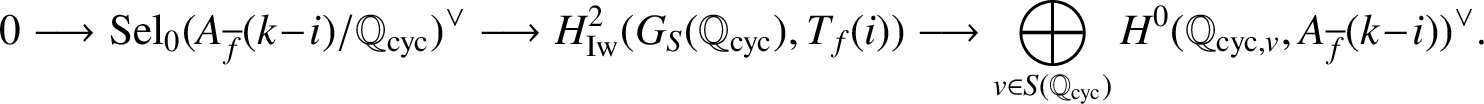 $$ \begin{align*} 0\longrightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k\!-\!i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee} \longrightarrow H^2_{\operatorname{\mathrm{Iw}}}(G_S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}), T_f(i)) \longrightarrow \bigoplus_{v \in S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}})} H^0(\mathbb{Q}_{\operatorname{\mathrm{cyc}},v}, A_{\overline{f}}(k\!-\!i))^\vee. \end{align*} $$
$$ \begin{align*} 0\longrightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k\!-\!i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee} \longrightarrow H^2_{\operatorname{\mathrm{Iw}}}(G_S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}), T_f(i)) \longrightarrow \bigoplus_{v \in S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}})} H^0(\mathbb{Q}_{\operatorname{\mathrm{cyc}},v}, A_{\overline{f}}(k\!-\!i))^\vee. \end{align*} $$
Therefore, the lemma follows from (H0).
Theorem 3.4. Suppose that f is nonordinary at p and (H0) holds. We have a pseudo-isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
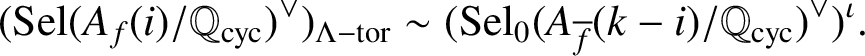 $$ \begin{align*} (\operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee)_{\Lambda-\mathrm{tor}}\sim (\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee)^\iota. \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee)_{\Lambda-\mathrm{tor}}\sim (\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee)^\iota. \end{align*} $$
Proof. Consider the defining sequence of the Selmer group
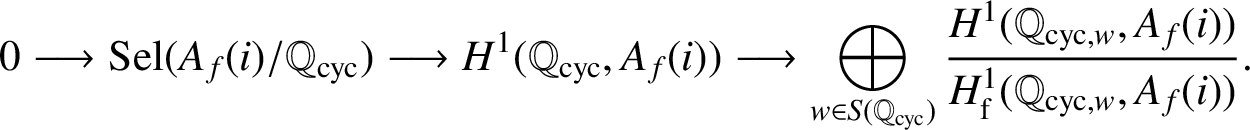 $$ \begin{align*} 0 \longrightarrow \operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}}) \longrightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_f(i)) \longrightarrow \bigoplus_{w\in S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}})} \frac{H^1(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))}{H^1_{\mathrm{f}}(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))}. \end{align*} $$
$$ \begin{align*} 0 \longrightarrow \operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}}) \longrightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_f(i)) \longrightarrow \bigoplus_{w\in S(\mathbb{Q}_{\operatorname{\mathrm{cyc}}})} \frac{H^1(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))}{H^1_{\mathrm{f}}(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))}. \end{align*} $$
By [Reference Bloch, Kato, Cartier, Illusie, Katz, Laumon, Manin and Ribet4, Proposition 3.8], there is an isomorphism
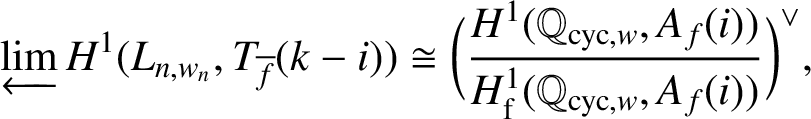 $$ \begin{align*}\varprojlim H^1(L_{n,w_n},T_{\overline{f}}(k-i))\cong\bigg( \frac{H^1(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))}{H^1_{\mathrm{f}}(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))} \bigg)^\vee,\end{align*} $$
$$ \begin{align*}\varprojlim H^1(L_{n,w_n},T_{\overline{f}}(k-i))\cong\bigg( \frac{H^1(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))}{H^1_{\mathrm{f}}(\mathbb{Q}_{\mathrm{cyc},w}, A_f(i))} \bigg)^\vee,\end{align*} $$
where
![]() $w_n\in S(L_n)$
is such that
$w_n\in S(L_n)$
is such that
![]() $w_n$
lies below w and
$w_n$
lies below w and
![]() $w_{n+1}$
. When
$w_{n+1}$
. When
![]() $w\nmid p$
, this is zero by [Reference Kato12, Section 17.10]. When
$w\nmid p$
, this is zero by [Reference Kato12, Section 17.10]. When
![]() $w \mid p$
, it is also zero by [Reference Perrin-Riou24, Theorem 0.6] under the hypothesis that f is nonordinary at p. Hence, we have an isomorphism
$w \mid p$
, it is also zero by [Reference Perrin-Riou24, Theorem 0.6] under the hypothesis that f is nonordinary at p. Hence, we have an isomorphism
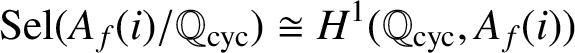 $$ \begin{align*} \operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}}) \cong H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_f(i))\end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}}) \cong H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}}, A_f(i))\end{align*} $$
of
![]() $\Lambda $
-modules. Combining this with Theorem 3.1, we obtain a pseudo-isomorphism
$\Lambda $
-modules. Combining this with Theorem 3.1, we obtain a pseudo-isomorphism
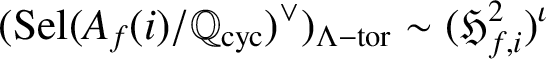 $$ \begin{align*} (\operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee)_{\Lambda-\mathrm{tor}} \sim (\mathfrak{H}^2_{f,i})^\iota\end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{Sel}}(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee)_{\Lambda-\mathrm{tor}} \sim (\mathfrak{H}^2_{f,i})^\iota\end{align*} $$
of
![]() $\Lambda $
-modules. But the latter is pseudo-isomorphic to
$\Lambda $
-modules. But the latter is pseudo-isomorphic to
![]() $\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
by Lemma 3.3 under (H0). This concludes the proof of the theorem.
$\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
by Lemma 3.3 under (H0). This concludes the proof of the theorem.
4 Comparison of characteristic elements
4.1 Preliminary lemmas
We prove several preliminary lemmas that will be used in the proofs of Theorems 4.3 and 4.4 below.
Lemma 4.1. Assume that (H0) holds. If F is an irreducible element of
![]() $\Lambda $
such that
$\Lambda $
such that
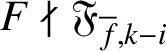 $F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
, then we have a psuedo-isomorphism
$F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
, then we have a psuedo-isomorphism
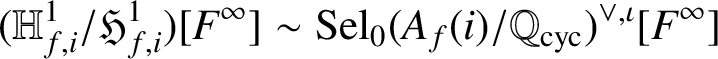 $$ \begin{align*} (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty]\sim \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee,\iota} [F^\infty] \end{align*} $$
$$ \begin{align*} (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty]\sim \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee,\iota} [F^\infty] \end{align*} $$
of
![]() $\Lambda $
-modules. In particular,
$\Lambda $
-modules. In particular,
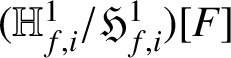 $(\mathbb {H}^1_{f,i}/\mathfrak {H}^1_{f,i})[F]$
is finite if and only if
$(\mathbb {H}^1_{f,i}/\mathfrak {H}^1_{f,i})[F]$
is finite if and only if
![]() $F^\iota \nmid \mathfrak {F}_{f,i}$
.
$F^\iota \nmid \mathfrak {F}_{f,i}$
.
Proof. We have the Poitou–Tate exact sequence
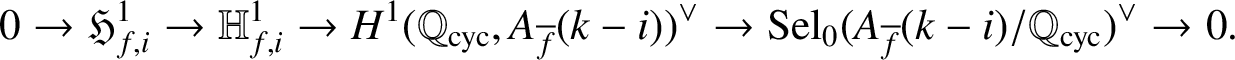 $$ \begin{align*} 0\rightarrow\mathfrak{H}^1_{f,i}\rightarrow\mathbb{H}^1_{f,i} \rightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\rightarrow 0. \end{align*} $$
$$ \begin{align*} 0\rightarrow\mathfrak{H}^1_{f,i}\rightarrow\mathbb{H}^1_{f,i} \rightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee\rightarrow 0. \end{align*} $$
This gives the short exact sequence
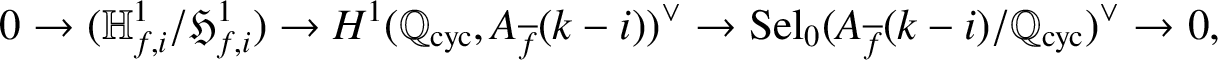 $$ \begin{align*} 0\rightarrow (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})\rightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee \rightarrow 0 ,\end{align*} $$
$$ \begin{align*} 0\rightarrow (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})\rightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee \rightarrow 0 ,\end{align*} $$
which in turn induces the exact sequence
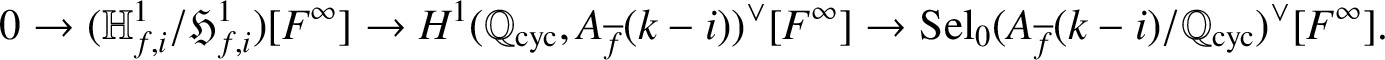 $$ \begin{align*} 0\rightarrow (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty]\rightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee[F^\infty]\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee[F^\infty]. \end{align*} $$
$$ \begin{align*} 0\rightarrow (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty]\rightarrow H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee[F^\infty]\rightarrow\operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^\vee[F^\infty]. \end{align*} $$
By assumption,
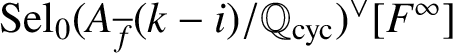 $\operatorname {\mathrm {Sel}}_0(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee [F^\infty ]$
is finite. Therefore, we obtain a psuedo-isomorphism
$\operatorname {\mathrm {Sel}}_0(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee [F^\infty ]$
is finite. Therefore, we obtain a psuedo-isomorphism
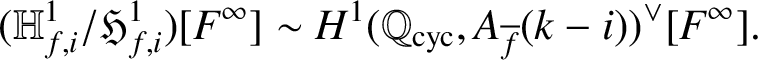 $$ \begin{align*} (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty]\sim H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee[F^\infty]. \end{align*} $$
$$ \begin{align*} (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty]\sim H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee[F^\infty]. \end{align*} $$
By Theorem 3.1 and Lemma 3.3, we have the pseudo-isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
 $$ \begin{align*} H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee[F^\infty]\sim \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee,\iota} [F^\infty]. \end{align*} $$
$$ \begin{align*} H^1(\mathbb{Q}_{\operatorname{\mathrm{cyc}}},A_{\overline{f}}(k-i))^\vee[F^\infty]\sim \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee,\iota} [F^\infty]. \end{align*} $$
Combining these two pseudo-isomorphisms finishes the proof of the lemma.
Lemma 4.2. Assume that (H-IMC) holds. Let F be an irreducible element of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $F\nmid \eta _{k,i}$
. Recall that
$F\nmid \eta _{k,i}$
. Recall that
![]() $\mathrm {loc}_p$
denotes the localisation map from
$\mathrm {loc}_p$
denotes the localisation map from
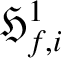 $\mathfrak {H}^1_{f,i}$
to
$\mathfrak {H}^1_{f,i}$
to
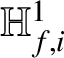 $\mathbb {H}^1_{f,i}$
. Then one has a pseudo-isomorphism
$\mathbb {H}^1_{f,i}$
. Then one has a pseudo-isomorphism
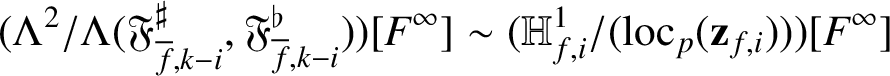 $$ \begin{align*} (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty] \sim (\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))) [F^\infty] \end{align*} $$
$$ \begin{align*} (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty] \sim (\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))) [F^\infty] \end{align*} $$
of
![]() $\Lambda $
-modules. Hence,
$\Lambda $
-modules. Hence,
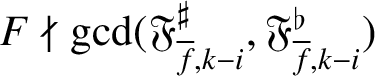 $F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
if and only if
$F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
if and only if
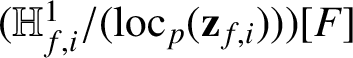 $ (\mathbb {H}^1_{f,i}/(\mathrm {loc}_p(\mathbf {z}_{f,i})))[F]$
is finite.
$ (\mathbb {H}^1_{f,i}/(\mathrm {loc}_p(\mathbf {z}_{f,i})))[F]$
is finite.
Proof. By (2.4) and (2.3), we have the exact sequence
 $$ \begin{align*} 0\rightarrow \mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))\rightarrow \Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat)\rightarrow \Lambda/\eta_{k,i}\rightarrow 0. \end{align*} $$
$$ \begin{align*} 0\rightarrow \mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))\rightarrow \Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat)\rightarrow \Lambda/\eta_{k,i}\rightarrow 0. \end{align*} $$
This gives the exact sequence
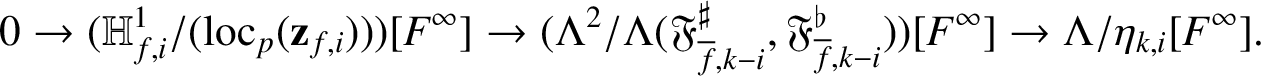 $$ \begin{align*} 0\rightarrow (\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i})))[F^\infty]\rightarrow (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty]\rightarrow \Lambda/\eta_{k,i}[F^\infty]. \end{align*} $$
$$ \begin{align*} 0\rightarrow (\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i})))[F^\infty]\rightarrow (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty]\rightarrow \Lambda/\eta_{k,i}[F^\infty]. \end{align*} $$
The last term is finite since
![]() $F\nmid \eta _{k,i}$
. Hence, the result follows.
$F\nmid \eta _{k,i}$
. Hence, the result follows.
4.2 Comparison between characteristic ideals of fine Selmer groups and signed Selmer groups
The goal of this section is to prove a generalisation of [Reference Lei and Sujatha18, Theorem 1.2] (see Theorem 4.4 below). We shall do so via the following intermediate result.
Theorem 4.3. Assume that (H-IMC) and (H0) hold. Let F be an irreducible element of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $F\nmid \eta _{k,i}$
and
$F\nmid \eta _{k,i}$
and
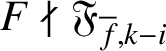 $F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
. There is a pseudo-isomorphism of
$F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
. There is a pseudo-isomorphism of
![]() $\Lambda $
-modules
$\Lambda $
-modules
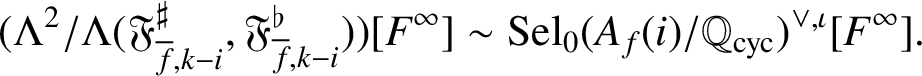 $$ \begin{align*} (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty] \sim \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee,\iota} [F^\infty]. \end{align*} $$
$$ \begin{align*} (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty] \sim \operatorname{\mathrm{Sel}}_0(A_f(i)/\mathbb{Q}_{\operatorname{\mathrm{cyc}}})^{\vee,\iota} [F^\infty]. \end{align*} $$
In particular,
![]() $F^\iota \nmid \mathfrak {F}_{f,i}$
if and only if
$F^\iota \nmid \mathfrak {F}_{f,i}$
if and only if
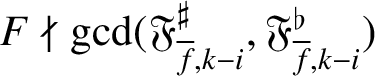 $F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
.
$F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
.
Proof. By Lemma 4.2, we have a pseudo-isomorphism
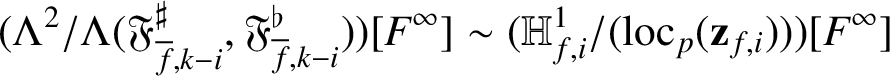 $$ \begin{align*} (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty] \sim (\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))) [F^\infty] \end{align*} $$
$$ \begin{align*} (\Lambda^2/\Lambda(\mathfrak{F}_{{\overline{f}},k-i}^\sharp,\mathfrak{F}_{{\overline{f}},k-i}^\flat))[F^\infty] \sim (\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))) [F^\infty] \end{align*} $$
of
![]() $\Lambda $
-modules. Consider the short exact sequence
$\Lambda $
-modules. Consider the short exact sequence
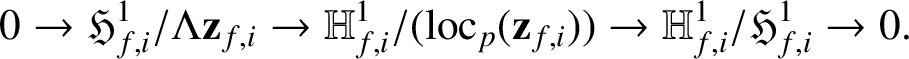 $$ \begin{align*} 0\rightarrow \mathfrak{H}^1_{f,i}/\Lambda\mathbf{z}_{f,i}\rightarrow \mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))\rightarrow \mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i}\rightarrow0. \end{align*} $$
$$ \begin{align*} 0\rightarrow \mathfrak{H}^1_{f,i}/\Lambda\mathbf{z}_{f,i}\rightarrow \mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i}))\rightarrow \mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i}\rightarrow0. \end{align*} $$
Since
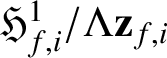 $\mathfrak {H}^1_{f,i}/\Lambda \mathbf {z}_{f,i}$
is a torsion
$\mathfrak {H}^1_{f,i}/\Lambda \mathbf {z}_{f,i}$
is a torsion
![]() $\Lambda $
-module with
$\Lambda $
-module with
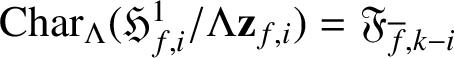 $\mathrm {Char}_\Lambda (\mathfrak {H}^1_{f,i}/\Lambda \mathbf {z}_{f,i}) = \mathfrak {F}_{{\overline {f}},k-i}$
not divisible by F, we have the following pseudo-isomorphism of
$\mathrm {Char}_\Lambda (\mathfrak {H}^1_{f,i}/\Lambda \mathbf {z}_{f,i}) = \mathfrak {F}_{{\overline {f}},k-i}$
not divisible by F, we have the following pseudo-isomorphism of
![]() $\Lambda $
-modules:
$\Lambda $
-modules:
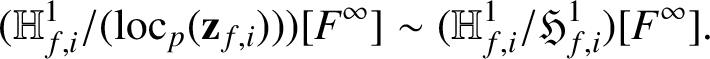 $$ \begin{align*}(\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i})))[F^\infty]\sim (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty] .\end{align*} $$
$$ \begin{align*}(\mathbb{H}^1_{f,i}/(\mathrm{loc}_p(\mathbf{z}_{f,i})))[F^\infty]\sim (\mathbb{H}^1_{f,i}/\mathfrak{H}^1_{f,i})[F^\infty] .\end{align*} $$
By Lemma 4.1, the latter is pseudo-isomorphic to
![]() $\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^{\vee ,\iota } [F^\infty ]$
. On combining these pseudo-isomorphisms, the theorem follows.
$\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^{\vee ,\iota } [F^\infty ]$
. On combining these pseudo-isomorphisms, the theorem follows.
We can now state and prove the main result of the article.
Theorem 4.4. Assume that (H-IMC) and (H0) hold. Let F be an irreducible element of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $F\nmid \eta _{k,i}$
. Then
$F\nmid \eta _{k,i}$
. Then
![]() $F^\iota \nmid \mathfrak {F}_{f,i}$
and
$F^\iota \nmid \mathfrak {F}_{f,i}$
and
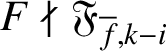 $F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
if and only if
$F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
if and only if
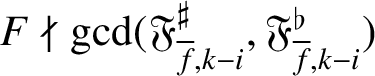 $F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
.
$F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
.
Proof. Theorem 4.3 tells us that if
![]() $F^\iota \nmid \mathfrak {F}_{f,i}$
and
$F^\iota \nmid \mathfrak {F}_{f,i}$
and
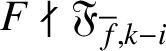 $F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
, then
$F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
, then
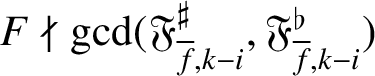 $F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
. This proves the ‘only if’ implication.
$F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
. This proves the ‘only if’ implication.
Conversely, suppose that
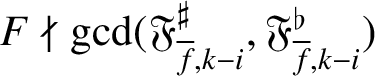 $F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
. From the inclusion
$F\nmid \gcd (\mathfrak {F}_{{\overline {f}},k-i}^\sharp ,\mathfrak {F}_{{\overline {f}},k-i}^\flat )$
. From the inclusion
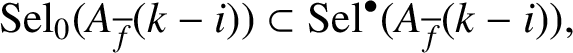 $$ \begin{align*} \operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i))\subset \operatorname{\mathrm{Sel}}^{\bullet}(A_{\overline{f}}(k-i)), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sel}}_0(A_{\overline{f}}(k-i))\subset \operatorname{\mathrm{Sel}}^{\bullet}(A_{\overline{f}}(k-i)), \end{align*} $$
we have
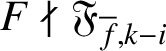 $F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
. The remaining assertion that
$F\nmid \mathfrak {F}_{{\overline {f}},k-i}$
. The remaining assertion that
![]() $F^\iota \nmid \mathfrak {F}_{f,i}$
now follows from Theorem 4.3.
$F^\iota \nmid \mathfrak {F}_{f,i}$
now follows from Theorem 4.3.
Remark 4.5. Let
![]() $E/\mathbb {Q}$
be an elliptic curve with good supersingular reduction at p. In [Reference Lei and Sujatha18], it is stated in the proof of Proposition 3.1 that by [Reference Wingberg, Coates, Greenberg, Mazur and Satake28, Corollary 2.5], we have the equality
$E/\mathbb {Q}$
be an elliptic curve with good supersingular reduction at p. In [Reference Lei and Sujatha18], it is stated in the proof of Proposition 3.1 that by [Reference Wingberg, Coates, Greenberg, Mazur and Satake28, Corollary 2.5], we have the equality
However, one of the two Selmer groups should be twisted by
![]() $\iota $
in order for the equality to hold. As such, for the rest of the proof to go through, the additional hypothesis that the irreducible element f (not to be confused with the notation for a modular form in the present article) satisfies
$\iota $
in order for the equality to hold. As such, for the rest of the proof to go through, the additional hypothesis that the irreducible element f (not to be confused with the notation for a modular form in the present article) satisfies
![]() $(f)=(f^\iota )$
is required. Consequently, the statement of [Reference Lei and Sujatha18, Theorem 1.2] should also be modified.
$(f)=(f^\iota )$
is required. Consequently, the statement of [Reference Lei and Sujatha18, Theorem 1.2] should also be modified.
Specialising our Theorem 4.4 to the case
![]() $F=\varpi $
, where
$F=\varpi $
, where
![]() $\varpi $
is a uniformiser of
$\varpi $
is a uniformiser of
![]() $\mathcal {O}$
, we may deduce the following result.
$\mathcal {O}$
, we may deduce the following result.
Corollary 4.6. Assume that (H-IMC) and (H0) hold. Then the following statements are equivalent.
-
(a) The
 $\mu $
-invariants of
$\mu $
-invariants of
 $\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
$\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
 $\operatorname {\mathrm {Sel}}_0(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
are zero.
$\operatorname {\mathrm {Sel}}_0(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
are zero. -
(b) At least one of
 $\operatorname {\mathrm {Sel}}^\sharp (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
$\operatorname {\mathrm {Sel}}^\sharp (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
 $\operatorname {\mathrm {Sel}}^\flat (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
has trivial
$\operatorname {\mathrm {Sel}}^\flat (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
has trivial
 $\mu $
-invariant.
$\mu $
-invariant.
Remark 4.7. From [Reference Coates and Sujatha7, Conjecture A], [Reference Jha and Sujatha11, Conjecture A] and [Reference Aribam1, Conjecture 1.2], the
![]() $\mu $
-invariants of
$\mu $
-invariants of
![]() $\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
$\operatorname {\mathrm {Sel}}_0(A_f(i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
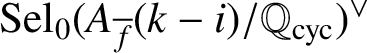 $\operatorname {\mathrm {Sel}}_0(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
are predicted always to vanish. Corollary 4.6 gives an alternative formulation of these conjectures in terms of signed Selmer groups. In fact, numerical calculations carried out by Pollack (see [Reference Pollack25, Section 7] and http://math.bu.edu/people/rpollack/Data/data.html) suggest that the
$\operatorname {\mathrm {Sel}}_0(A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
are predicted always to vanish. Corollary 4.6 gives an alternative formulation of these conjectures in terms of signed Selmer groups. In fact, numerical calculations carried out by Pollack (see [Reference Pollack25, Section 7] and http://math.bu.edu/people/rpollack/Data/data.html) suggest that the
![]() $\mu $
-invariants of both
$\mu $
-invariants of both
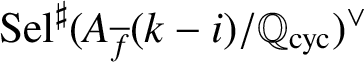 $\operatorname {\mathrm {Sel}}^\sharp (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
$\operatorname {\mathrm {Sel}}^\sharp (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
and
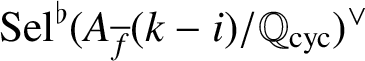 $\operatorname {\mathrm {Sel}}^\flat (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
are zero when
$\operatorname {\mathrm {Sel}}^\flat (A_{\overline {f}}(k-i)/\mathbb {Q}_{\operatorname {\mathrm {cyc}}})^\vee $
are zero when
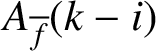 $A_{\overline {f}}(k-i)$
is given by
$A_{\overline {f}}(k-i)$
is given by
![]() $E[p^\infty ]$
for some elliptic curve
$E[p^\infty ]$
for some elliptic curve
![]() $E/\mathbb {Q}$
with good supersingular reduction at p.
$E/\mathbb {Q}$
with good supersingular reduction at p.
Acknowledgement
We would like to thank the anonymous referee for providing various helpful comments that have helped us improve the exposition of this article.