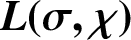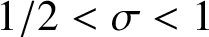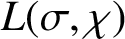Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Qiyu
2024.
Large values of ζ(s) for 1/2 < Re(s)<1.
Journal of Number Theory,
Vol. 254,
Issue. ,
p.
199.