Research Article
On non-linear elliptic equations and the stability of soap film
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-361
-
- Article
-
- You have access
- Export citation
Centralisers of Galois group actions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 363-365
-
- Article
-
- You have access
- Export citation
Perfect codes on the towers of Hanoi graph
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-376
-
- Article
-
- You have access
- Export citation
Quasi-convex functions and Hadamard's inequality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-385
-
- Article
-
- You have access
- Export citation
Semigroup rings in semisimple varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-391
-
- Article
-
- You have access
- Export citation
Curves with continuous Curvatures in Euclidean spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 393-401
-
- Article
-
- You have access
- Export citation
Finite-dimensional simple modules over quantised Weyl algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 403-408
-
- Article
-
- You have access
- Export citation
The predual of the space of convolutors on a locally compact group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 409-414
-
- Article
-
- You have access
- Export citation
Structural implications of norms with Hölder right-hand derivatives.
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 415-425
-
- Article
-
- You have access
- Export citation
PF-rings of generalised power series
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 427-432
-
- Article
-
- You have access
- Export citation
Iteration processes for approximating fixed points of operators of monotone type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-445
-
- Article
-
- You have access
- Export citation
An oscillation estimate to a variational inequality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 447-454
-
- Article
-
- You have access
- Export citation
On a theorem of Bryce and Cossey
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 455-460
-
- Article
-
- You have access
- Export citation
The reduced group C*-algebra of a triangle building
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 461-478
-
- Article
-
- You have access
- Export citation
The modular counterparts of Cayley's hyperdeterminants
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 479-492
-
- Article
-
- You have access
- Export citation
Quotients of permutation groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 493-495
-
- Article
-
- You have access
- Export citation
Exponential actions, orbits and their kernels
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 497-513
-
- Article
-
- You have access
- Export citation
On the conjecture of Jesmanowicz concerning Pythagorean triples
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 515-524
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
Tests based on sample partial autocorrelations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 525-527
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 57 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation

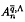 over an algebraically closed field under a certain condition on the parameters.
over an algebraically closed field under a certain condition on the parameters.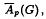 is a Banach algebra of functions on
is a Banach algebra of functions on 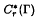 is simple. To prove this result we use the sufficient condition for the simplicity of
is simple. To prove this result we use the sufficient condition for the simplicity of 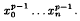
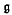 be a nilpotent Lie algebra which is an exponential
be a nilpotent Lie algebra which is an exponential 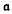 -module,
-module, 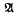 = exp
= exp 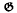 = exp
= exp