Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-10T06:10:27.928Z Has data issue: false hasContentIssue false
  • English
  • Français

The reduced group C*-algebra of a triangle building

Published online by Cambridge University Press:  17 April 2009

A.M. Mantero  and
Z. Zappa
A.M. Mantero
Affiliation:
Istituto di Discipline scientifiche e tecnicheFacoltà di ArchitetturaUniversità di Genova, 16123 GenovaItaly, e-mail: [email protected]
Z. Zappa
Affiliation:
Dipartimento di MatematicaUniversità di Genova, 16146 GenovaItaly, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Δ be an affine building of type Ã2 and let Γ be a discrete group of type-rotating automorphisms acting simply transitively on the vertices of δ. We prove that the reduced group C*-algebra 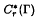is simple. To prove this result we use the sufficient condition for the simplicity of 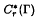given in a recent paper by M. Bekka, M. Cowling and P. de la Harpe.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 57 , Issue 3 , June 1998 , pp. 461 - 478
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Bekka, M., Cowling, M. and Harpe, P. de la, ‘Groups whose reduced group C*-algebra is simple’, Inst. Hautes. Études. Sci. Publ. Math. 80 (1994), 117–134.CrossRefGoogle Scholar
[2]Cartwright, D.I., Mantero, A.M., Steger, T. and Zappa, A., ‘Groups acting simply transitively on the vertices of a building of type Ã2’, Geom. Dedicata 47 (1993), 143–166.CrossRefGoogle Scholar
[3]Cartwright, D.I. and Mlotkowski, W., ‘Harmonic analysis for groups acting on triangle buildings’, J. Austral. Math. Soc. Ser. A 56 (1994), 345–383.CrossRefGoogle Scholar
[4]Cartwright, D.I., Mlotkowski, W. and Steger, T., ‘Property (T) and Ã2 groups’, Ann. Inst. Fourier 44 (1994), 213–248.CrossRefGoogle Scholar
[5]Mantero, A.M. and Zappa, A., ‘Spherical functions and spectrum of the Laplace operators on buildings of rank 2’, Boll. Un. Mat. Ital., 7 (1994), 419–475.Google Scholar
[6]Mozes, S., ‘Actions of Cartan subgroups’, Israel J. Math. 90 (1995), 253–294.CrossRefGoogle Scholar
[7]Powers, R.T., ‘Simplicity of the C*-algebra associated with the free group on two generators’, Duke Math. J. 42 (1975), 151–156.CrossRefGoogle Scholar
[8]Ramagge, J. and Robertson, G., ‘Triangle buildings and actions of type III 1/q 2’, J. Fund. Anal. 140 (1996), 472–504.CrossRefGoogle Scholar
[9]Robertson, G. and Steger, T., ‘C*-algebras arising from group actions on the boundary of a triangle building’, Proc. London Math. Soc. 72 (1996), 613–637.CrossRefGoogle Scholar
[10]Ronan, M.A., Lectures on buildings, Perspectives in Math. 7 (Academic Press, London, 1989).Google Scholar