In this paper we study the Cauchy problem for the second order nonlinear hyperbolic partial differential equation
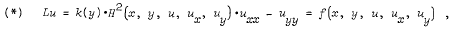
with initial conditions
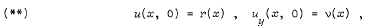
where
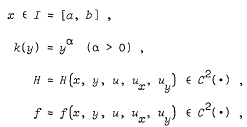
and |u|, |ux|, |uy| < ∞, y ≥ 0, r = r(x) ∈ C4(·), ν = ν(x) ∈ C4(·).
These conditions on k, H, f, r, and ν are assumed to be satisfied in some sufficiently small neighborhood of the segment I, y = 0, in the upper half-plane y > 0
This paper generalizes the results obtained by N.A. Lar'kin (Differencial'nye Uravnenija 8 (1972), 76–84), who has treated the special case H = H(x, y, u); that is, the quasi-linear hyperbolic equation (*).