Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-07T14:24:48.764Z Has data issue: false hasContentIssue false
  • English
  • Français

The Cauchy problem for a second-order nonlinear hyperbolic equation with initial data on a line of parabolicity

Published online by Cambridge University Press:  17 April 2009

John M.S. Rassias
John M.S. Rassias
Affiliation:
II Dervenakion Str, Daphne, Athens, Greece.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the Cauchy problem for the second order nonlinear hyperbolic partial differential equation

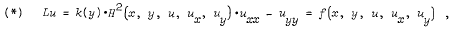
with initial conditions

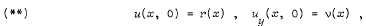
where

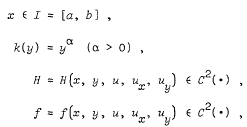
and |u|, |ux|, |uy| < ∞, y ≥ 0, r = r(x) ∈ C4(·), ν = ν(x) ∈ C4(·).

These conditions on k, H, f, r, and ν are assumed to be satisfied in some sufficiently small neighborhood of the segment I, y = 0, in the upper half-plane y > 0

This paper generalizes the results obtained by N.A. Lar'kin (Differencial'nye Uravnenija 8 (1972), 76–84), who has treated the special case H = H(x, y, u); that is, the quasi-linear hyperbolic equation (*).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 20 , Issue 3 , June 1979 , pp. 345 - 365
Copyright
Copyright © Australian Mathematical Society 1979

References

[1]Березин, И.С. [I.S. Berezin], “О задаче Коши для линейного уравнения второго порядка с начальными данными на линии параболичности” [On Cauchy's problem for linear equations of the second order with initial conditions on a parabolic line], Mat. Sb. 24 (66) (1949), 301–320.Google ScholarPubMed
[2]Bers, L., “On the continuation of a potential gas flow across the sonic line” (NACA Technical Note 2058, 1950).Google Scholar
[3]Birkhoff, Garrett, Rota, Gian-Carlo, Ordinary differential equations (Ginn, Boston, New York, Chicago, Atlanta, Dallas, Palo Alto, Toronto, 1962).Google Scholar
[4]Bitsadze, A.V., Equations of the mixed type (translated by Zador, P.. Macmillan, New York, 1964).Google Scholar
[5]Coddington, Earl A. and Levinson, Norman, Theory of ordinary differential equations (McGraw-Hill, New York, Toronto, London, 1955).Google Scholar
[6]Conti, Roberto, “Sul problema di Cauchy per l'equazione y 2αk 2(x, y)·zxx − zyy = f(x, y, z, zx, zy), con i dati sulla linea parabolica”, Ann. Mat. Pura Appl. 31 (1950), 303–326.CrossRefGoogle Scholar
[7]Courant, Richard and Lax, Peter, “On nonlinear partial differential equations with two independent variables”, Comm. Pure Appl. Math. 2 (1949), 255–273.CrossRefGoogle Scholar
[8]Франкль, Ф.И. [F.I. Frankl'], “ О задаче Коши для уравнений смешанного зллнптико-гиперболического типа с качальными данными на пеоеходиой линии” [On Cauchy's problem for partial differential equations of mixed elliptic-hyperbolic type with initial data on the parabolic line], Bull. Acad. Sci. URSS Ser. Math. [Izv. Akad. Nauk SSSR] 8 (1953), 195–224.Google ScholarPubMed
[9]Germain, P. et Bader, R., “Solutions éléementaires de certaines équations aux dérivées partielles du type mixte”, Bull. Soc. Math. France 81 (1953), 145–174.CrossRefGoogle Scholar
[10]Ларькин, Н.А. [N.A. Lar'kin], “О задаче Коши для квазилинейного гиперболического уравнения второго порядка с начальными данными на линии параболичности” [The Cauchy problem for a second order quasilinear hyperbolic equation with initial data on the curve of parabolicity], Differencial'nye Uravnenija 8 (1972), 76–84.Google ScholarPubMed
[11]Lick, Dale W., “A uniqueness theorem for a singular Cauchy problem”, Ann. Mat. Pura Appl. (4) 72 (1966), 267–274.CrossRefGoogle Scholar
[12]Lick, Dale W., “A quasi-linear singular Cauchy problem”, Ann. Mat. Pura Appl. (4) 74 (1966), 113–128.CrossRefGoogle Scholar
[13]Lick, Dale W., “A singular Cauchy problem”, J. Math. Anal. Appl. 28 (1969), 93–99.CrossRefGoogle Scholar
[14]Мередов, М. [M. Meredov], “ Об однозначной разрешимости задачи Дарбу для одной вырождающейся системы” [The unique solvability of the Darboux problem for a certain degenerate system], Differencial'nye Uravnenija 10 (1974), 89–99.Google ScholarPubMed
[15]Ogawa, Hajimu, “The singular Cauchy problem for a quasi-linear hyperbolic equation of second order”, J. Math. Meeh. 12 (1963), 847–856.Google Scholar
[16]Ogawa, Hajimu, “On the unique solution of the singular Cauchy problem for a quasi-linear equation”, Ann. Mat. Pura Appl. (4) 66 (1964), 391–403.CrossRefGoogle Scholar
[17]Ogawa, Hajimu, “A nonlinear singular Cauchy problem”, J. Math. Anal. Appl. 13 (1966), 527–535.CrossRefGoogle Scholar
[18]Protter, M.H., “The Cauchy problem for a hyperbolic second order equation with data on the parabolic line”, Canad. J. Math. 6 (1954), 542–553.CrossRefGoogle Scholar
[19]Schauder, J., “Der Fixpunktsatz in Funktionalräumen”, Studia Math. 2 (1930), 171–180.CrossRefGoogle Scholar
[20]Singer, Seymour, “The singular Cauchy problem for a nonlinear hyperbolic equation” (PhD thesis, University of California, Berkeley, 1969).Google Scholar
[21]Терсенов, С.А. [S.A. Tersenov], “ К теории гиперболических уравнений с данными на линии вырождения типа” [On the theory of hyperbolic equations with data on a line of degeneration type], Sibirsk. Mat. ž. 2 (1961), 913–935.Google ScholarPubMed