Let f be a real function defined on [0, 1] × R3 and let η ∈ (0, 1). Very recently, C.P. Gupta and V. Lakshimikantham, making use of the Leray-Schauder continuation theorem and Wirtinger-type inequalities, established an existence result for the problem

(Theorem 1 and Remark 4 of [Nonlinear Anal. 16 (1991), 949–957]).

The aim of the present paper is simply to point out how, bu means of a completely different approach, it is possible to improve that result not only by requiring much general on f, but also by giving a precise pointwise estimate on x″′

The uniqueness of limit cycles is proved for quadratic systems with an invariant parabola and for cubic systems with four real line invariants. Also a new, simple proof is given of the uniqueness of limit cycles occurring in unfoldings of certain vector fields with codimension two singularities.

It is shown that the well-known theorem of Kadec for the HГ renorming of separable Banach spaces, when Г is a norming subspace in the dual, cannot be extended to the class of nonseparable Banach spaces.

In this paper we show that for a compact connected abelian group G the near-ring [G, G] of all homotopy classes of continuous selfmaps of G is an abstract affine near-ring, and investigate the ideal structure of these near-rings.

Modules whose nonzero endomorphisms are epimorphisms and modules whose nonzero endomorphisms are monomorphisms are considered in this paper. We prove that these two classes of modules are dual to each other via Morita duality. We also prove that a left artinian ring R with Jacobson radical J has a Morita duality if either (1) J/J2 is a central bimodule; or (2) R is artinian right duo and R/J is commutative.

The purpose of this note is to give a general existence theorem for maximal elements for a new type of preference correspondences which are u-majorised. As an application, an existence theorem of equilibria for a qualitative game is obtained in which the preferences are u-majorised with an arbitrary (countable or uncountable) set of players and without compactness assumption on their domains in Hausdorff locally convex topological vector spaces.

It is proved that the upper radical determined by the class of prime essential rings is an N-radical.

Let G be a nondiscrete locally compact Hausdorff abelian group. It is shown that if G contains an open torsion subgroup, then every proper dense subgroup of G is contained in a maximal subgroup; while if G has no open torsion subgroup, then it has a dense subgroup D such that G/D is algebraically isomorphic to R, the additive group of reals. With each G, containing an open torsion subgroup, we associate the least positive integer n such that the nth multiple of every discontinuous character of G is continuous. The following are proved equivalent for a nondiscrete locally compact abelian group G:

(1) The intersection of any two dense subgroups of G is dense in G.

(2) The intersection of all dense subgroups of G is dense in G.

(3) G contains an open torsion subgroup, and for each prime p dividing the positive integer associated with G, pG is either open or a proper dense subgroup of G.

Finally, we construct a locally compact abelian group G with infinitely many dense subgroups satisfying the three equivalent conditions stated above.

In this paper, some necessary and sufficient conditions for oscillation of a first order delay differential equation with oscillating coefficients of the form

are established. Several applications of our results improve and generalise some of the known results in the literature.

In this paper, we characterise all primitive ideals of the quantised enveloping algebra Uq[sl(2, ℂ)] of the complex Lie algebra sl(2, ℂ) and show how they are similar to those of U[sl(2, ℂ)], the enveloping algebra of sl(2, ℂ).

Let D be a skew field with uncountable centre K. The main result in the present paper is as follows: If D satisfies a non-trivial generalised power central rational identity, then D is finite dimensional over K. As a corollary we obtain the following result. Let a be an element of D such that (a−1x−1ax)q(x) ∈ K for all x ∈ D ﹨ {0} where q(x) is a positive integer depending on x. Then a ∈ K.

We extend the results of N.K. Ribarska and A.V. Arhangel'skiĭ to the class of strongly countably complete spaces. And we show another characterisation of Eberlein and Radon-Nikodým compact spaces.

If f(x) is defined on [−1, 1], let H¯1 n(f, x) denote the Lagrange interpolation polynomial of degree n (or less) for f which agrees with f at the n+1 equally spaced points xk, n = −1 + (2k)/n (0 ≤ k ≤ n). A famous example due to S. Bernstein shows that even for the simple function h(x) = │x│, the sequence H¯1 n (h, x) diverges as n → ∞ for each x in 0 < │x│ < 1. A generalisation of Lagrange interpolation is the Hermite-Fejér interpolation polynomial H¯mn (f, x), which is the unique polynomial of degree no greater than m(n + 1) – 1 which satisfies 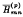(f, Xk, n) = δo, pf(xk, n) (0 ≤ p ≤ m − 1, 0 ≤ k ≤ n). In general terms, if m is an even number, the polynomials H¯mn(f, x) seem to possess better convergence properties than the H¯1 n (f, x). Nevertheless, D.L. Berman was able to show that for g(x) ≡ x, the sequence H¯2n(g, x) diverges as n → ∞ for each x in 0 < │x│. In this paper we extend Berman's result by showing that for any even m, H¯mn(g, x) diverges as n → ∞ for each x in 0 < │x│ < 1. Further, we are able to obtain an estimate for the error │H¯mn(g, x) – g(x)│.

The aim of this note is to present in the reflexive Banach space setting a natural and simple proof of the formula of the approximate subdifferential of a composite function.

A non-pathological example is given of two topological spaces which have isomorphic homotopy groups, homology groups and cohomology ring and which cannot be distinguished from each other by the Whitehead product structure. A family of examples can be constructed likewise.

In this paper we investigate the situation where a group G has an abelian subgroup H with connected transversals. We show that if H is finite then G is solvable. We also investigate some special cases where the structure of H is very close to the structure of a cyclic group. Finally we apply our results to loop theory and we show that if the inner mapping group of a finite loop Q is abelian then Q is centrally nilpotent.

Nonsmooth calculus using the approximate subdifferential of Mordukhovich and loffe admits a sharper chain rule, hence sharper applications in optimisation, than does the generalised gradient of Clarke. We observe, however, that at a local minimum point of the composition of nonsmooth vector valued and real valued functions, the generalised gradient admits a special, relatively sharp chain rule, that yields sharper results than have been seen before in the context of the generalised gradient.

Some characterisations of generalised convex functions are established by means of Clarke's subdifferential and directional derivatives.

It has been conjectured by R. S. Ward that the self-dual Yang-Mills Equations (SDYMEs) form a “master system” in the sense that most known integrable ordinary and partial differential equations are obtainable as reductions. We systematically construct the group of symmetries of the SDYMEs on R4 with semisimple gauge group of finite dimension and show that this yields only the well known gauge and conformal symmetries.

In this note we characterise finitely generated self-projective R-modules M satisfying the property that every non-zero M-singular. R-module contains a non-zero M-injective submodule.