If f(x) is defined on [−1, 1], let H¯1 n(f, x) denote the Lagrange interpolation polynomial of degree n (or less) for f which agrees with f at the n+1 equally spaced points xk, n = −1 + (2k)/n (0 ≤ k ≤ n). A famous example due to S. Bernstein shows that even for the simple function h(x) = │x│, the sequence H¯1 n (h, x) diverges as n → ∞ for each x in 0 < │x│ < 1. A generalisation of Lagrange interpolation is the Hermite-Fejér interpolation polynomial H¯mn (f, x), which is the unique polynomial of degree no greater than m(n + 1) – 1 which satisfies 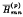(f, Xk, n) = δo, pf(xk, n) (0 ≤ p ≤ m − 1, 0 ≤ k ≤ n). In general terms, if m is an even number, the polynomials H¯mn(f, x) seem to possess better convergence properties than the H¯1 n (f, x). Nevertheless, D.L. Berman was able to show that for g(x) ≡ x, the sequence H¯2n(g, x) diverges as n → ∞ for each x in 0 < │x│. In this paper we extend Berman's result by showing that for any even m, H¯mn(g, x) diverges as n → ∞ for each x in 0 < │x│ < 1. Further, we are able to obtain an estimate for the error │H¯mn(g, x) – g(x)│.