Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T02:44:02.467Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on a third-order three-point boundary value problem

Published online by Cambridge University Press:  17 April 2009

Salvatore A. Marano
Salvatore A. Marano
Affiliation:
Dipartimento di Matematica Città, Universitaria Viale, A. Doria 6, 95125 Catania, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let f be a real function defined on [0, 1] × R3 and let η ∈ (0, 1). Very recently, C.P. Gupta and V. Lakshimikantham, making use of the Leray-Schauder continuation theorem and Wirtinger-type inequalities, established an existence result for the problem

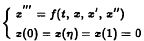
(Theorem 1 and Remark 4 of [Nonlinear Anal. 16 (1991), 949–957]).

The aim of the present paper is simply to point out how, bu means of a completely different approach, it is possible to improve that result not only by requiring much general on f, but also by giving a precise pointwise estimate on x″′

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 49 , Issue 1 , February 1994 , pp. 1 - 5
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Agarwal, R.P., Boundary value problems for higher order differential equations (World Scientific, 1986).CrossRefGoogle Scholar
[2]Diestel, J. and Uhl, J.J. Jr, Vector measures, Math. Surveys 15 (American Mathematical Society, Providence, R.I., 1977).CrossRefGoogle Scholar
[3]Gupta, C.P. and Lakshmikantham, V., ‘Existence and uniqueness theorems for a third-order three-point boundary value problem’, Nonlinear Anal. 16 (1991), 949–957.Google Scholar
[4]Köthe, G., Topological vector spaces-I (Springer-Verlag, Berlin, Heidelberg, New York, 1969).Google Scholar