Subject three
Sur la détermination de la réserve pour sinistres en suspens dans l'assurance automobile
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 199-209
-
- Article
-
- You have access
- Export citation
Astin Colloquium 1966 Arnhem Subject one
The unearned no claim bonus
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 25-32
-
- Article
-
- You have access
- Export citation
Research Article
A discipline for the avoidance of unnecessary assumptions 1
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 374-387
-
- Article
-
- You have access
- Export citation
Astin Colloquium 1966 Arnhem Subject one
A practical application of credibility to experience rating plans for hospitalization and medical-surgical insurance
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 33-40
-
- Article
-
- You have access
- Export citation
Subject three
Estimating incurred claims
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 210-212
-
- Article
-
- You have access
- Export citation
Astin Colloquium 1966 Arnhem Subject one
On automobile insurance ratemaking
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 41-48
-
- Article
-
- You have access
- Export citation
Research Article
Estimation of the number of excess claims by means of the credibility theory
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 388-392
-
- Article
-
- You have access
- Export citation
Subject three
Approximations of the generalised Poisson function
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 213-226
-
- Article
-
- You have access
- Export citation
Procedures and basic statistics to be used in magnitude control of equalisation reserves in Finland
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 227-238
-
- Article
-
- You have access
- Export citation
Astin Colloquium 1966 Arnhem Subject two
Applications of methods of operations research and modern economic theory
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 51-61
-
- Article
-
- You have access
- Export citation
Research Article
Insurance as a cybernetic institution of self-regulation of the national economy
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 393-401
-
- Article
-
- You have access
- Export citation
Astin Colloquium 1966 Arnhem Subject two
Driving with markov-programming
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 62-86
-
- Article
-
- You have access
- Export citation
Front matter
ASB volume 5 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Subject three
Estimation of the coefficient of variation of the excess of loss by means of Jensen's inequality for convex functions. The connection with the theory of life times
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 239-248
-
- Article
-
- You have access
- Export citation
Astin Colloquium 1966 Arnhem Subject two
Utilisation pratique de la methode de simulation dans l'assurance „non life”
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 87-117
-
- Article
-
- You have access
- Export citation
Subject three
On a class of measures of dispersion with application to optimal reinsurance
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 249-266
-
- Article
-
- You have access
- Export citation
Back matter
ASB volume 5 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 29 August 2014, p. b1
-
- Article
-
- You have access
- Export citation
Subject three
Methods of studying the risk process in disability insurance
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 267-273
-
- Article
-
- You have access
- Export citation
Astin Colloquium 1966 Arnhem Subject two
Dynamic decision problems in an insurance company
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 118-131
-
- Article
-
- You have access
- Export citation
Subject three
“Estimating incurred claims”
-
- Published online by Cambridge University Press:
- 29 August 2014, pp. 274-279
-
- Article
-
- You have access
- Export citation



 .
.
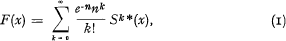
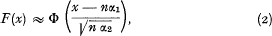

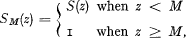
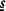 has distribution function
has distribution function 