One of the basic functions of risk theory is the so-called generalised Poisson function F(x), which gives the probability that the total amount of claims ξ does not exceed some given limit x during a year (or during some other fixed time period). For F(x) is obtained the well known expansion

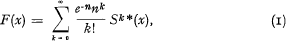
where n is the expected number of claims during this time period and Sk*(x) is the k:th convolution of the distribution function S(z) of the size of one claim. The formula (1) is, however, much too inconvenient for numerical computations and for most other applications. One of the main problems of risk theory, which is still partly open, is to find suitable methods to compute, or at least to approximate, the generalised Poisson function.

A frequently used approximation is to replace F(x) by the normal distribution function having the same mean and standard deviation as F as follows:

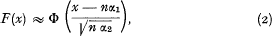
where α1 and α2 are the first zero-moments of S(z):

SM(Z) is here again the distribution function of the size of one claim. To obtain more general results a reinsurance arrangement is assumed under which the maximum net retention is M. Hence the portfolio on the company's own retention is considered. If the reinsurance is of Excess of Loss type, then

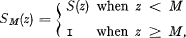
where S(z) is the distribution function of the size of one total claim.