1. In a paper presented to the fifth Astin Colloquium (Lucerne, 1965) Bühlmann has given some propositions with regard to Experience Rating understood as a sequence of estimates of the expectation with respect to the distribution function of θ, H(θ) say, of μ(θ) which is the mean for fixed θ with respect to the distribution function G(x; θ) of the variables 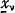 for each value of ν = 1, 2 … n. In such problems the estimator function for μ(θ) is generally chosen to be the conditional mean of μ(θ) for a given set of observed values of
for each value of ν = 1, 2 … n. In such problems the estimator function for μ(θ) is generally chosen to be the conditional mean of μ(θ) for a given set of observed values of 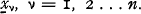 This is generally justified by the principle of least square deviation. According to Bühlmann this justification is not sufficient. Therefore, he bases the choice of this estimator function upon a postulate of equilibrium, described in the following lines.
This is generally justified by the principle of least square deviation. According to Bühlmann this justification is not sufficient. Therefore, he bases the choice of this estimator function upon a postulate of equilibrium, described in the following lines.
Let X′ be a subset of X, and C(X′) a cylinder with the base X′ ⊂ X in the product space X × Θ, where X is the set of all possible 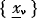 and Θ the set of all possible θ, then the postulate of equilibrium implies the equality between the expectations of μ(θ) and of a function of
and Θ the set of all possible θ, then the postulate of equilibrium implies the equality between the expectations of μ(θ) and of a function of 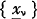 on each cylinder C(X′). This is exactly Kolmogoroff's definition of the conditional expectation:
on each cylinder C(X′). This is exactly Kolmogoroff's definition of the conditional expectation:
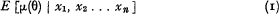
Bühlmann states, further, that the best linear estimate of (1) based on the arithmetic mean 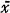 of n sample values xν of
of n sample values xν of 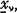 ν = 1, 2 … n can be written in the form of the Credibility Formula:
ν = 1, 2 … n can be written in the form of the Credibility Formula:

where the symbol E[·] denotes the expectation over the product space X × Θ and
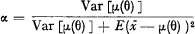
If the 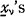 are independent and identically distributed, this leads to
are independent and identically distributed, this leads to 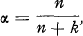 where k = E [σ2 (θ)] / Var [ν(θ)], and σ2(θ) is the variance for a fixed θ of G(x; θ). This case of the credibility formula is, generally, applied in American practice. (The proposition has later been proved for more general conditions).
where k = E [σ2 (θ)] / Var [ν(θ)], and σ2(θ) is the variance for a fixed θ of G(x; θ). This case of the credibility formula is, generally, applied in American practice. (The proposition has later been proved for more general conditions).