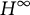 $H^{\infty }$ symbols
$H^{\infty }$ symbols
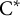 $\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
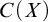 $C(X)$ WITH
$C(X)$ WITH 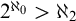 $2^{\aleph _0}>\aleph _2$
$2^{\aleph _0}>\aleph _2$
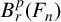 $B^p_r(F_n)$ HAS NO NONTRIVIAL IDEMPOTENTS
$B^p_r(F_n)$ HAS NO NONTRIVIAL IDEMPOTENTS
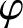 $\varphi $
-AMENABILITY OF DUAL BANACH ALGEBRAS
$\varphi $
-AMENABILITY OF DUAL BANACH ALGEBRAS