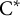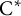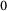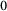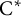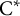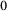1 Introduction and main results
In this article, we consider certain classes of
![]() $\mathrm{C}^{*}$
-algebras, extending the class of purely infinite
$\mathrm{C}^{*}$
-algebras, extending the class of purely infinite
![]() $\mathrm{C}^{*}$
-algebras and contained in the class of
$\mathrm{C}^{*}$
-algebras and contained in the class of
![]() $\mathrm{C}^{*}$
-algebras such that every nonzero hereditary
$\mathrm{C}^{*}$
-algebras such that every nonzero hereditary
![]() $\mathrm{C}^{*}$
-subalgebra has nonzero, square-zero, elements (see Figure 1). Our motivation for introducing these classes is to find (partial) answers to the following three open problems.
$\mathrm{C}^{*}$
-subalgebra has nonzero, square-zero, elements (see Figure 1). Our motivation for introducing these classes is to find (partial) answers to the following three open problems.

Figure 1 Classes of
![]() $\mathrm{C}^{*}$
-algebras with the property (HS
$\mathrm{C}^{*}$
-algebras with the property (HS
![]() $_0$
).
$_0$
).
![]() $(1)$
In [Reference Kirchberg and Rørdam7], Kirchberg and Rørdam introduced and compared three different notions of infiniteness for a
$(1)$
In [Reference Kirchberg and Rørdam7], Kirchberg and Rørdam introduced and compared three different notions of infiniteness for a
![]() $\mathrm{C}^{*}$
-algebra (namely, the properties of being strongly purely infinite, purely infinite, or weakly purely infinite). Later in [Reference Blanchard and Kirchberg2], Blanchard and Kirchberg also introduced the notion of being locally purely infinite, as a generalization of weak pure infiniteness. They asked whether these properties are all equivalent for any
$\mathrm{C}^{*}$
-algebra (namely, the properties of being strongly purely infinite, purely infinite, or weakly purely infinite). Later in [Reference Blanchard and Kirchberg2], Blanchard and Kirchberg also introduced the notion of being locally purely infinite, as a generalization of weak pure infiniteness. They asked whether these properties are all equivalent for any
![]() $\mathrm{C}^{*}$
-algebra. Pasnicu and the third author in [Reference Pasnicu and Rouzbehani10, Theorem 3.10], and the second and third authors in [Reference Elliott and Rouzbehani3, Theorem 2.1], showed that for
$\mathrm{C}^{*}$
-algebra. Pasnicu and the third author in [Reference Pasnicu and Rouzbehani10, Theorem 3.10], and the second and third authors in [Reference Elliott and Rouzbehani3, Theorem 2.1], showed that for
![]() $\mathrm{C}^{*}$
-algebras with topological dimension zero, the properties of being weakly purely infinite, purely infinite, or strongly purely infinite are equivalent.
$\mathrm{C}^{*}$
-algebras with topological dimension zero, the properties of being weakly purely infinite, purely infinite, or strongly purely infinite are equivalent.
![]() $(2)$
The global Glimm problem asks if every nowhere scattered
$(2)$
The global Glimm problem asks if every nowhere scattered
![]() $\mathrm{C}^{*}$
-algebra has the global Glimm property. (These properties are recalled below.) The other direction is known: a
$\mathrm{C}^{*}$
-algebra has the global Glimm property. (These properties are recalled below.) The other direction is known: a
![]() $\mathrm{C}^{*}$
-algebra with the global Glimm property is nowhere scattered (see [Reference Thiel and Vilalta15]). Thiel and Vilalta in [Reference Thiel and Vilalta15, Theorem 7.1] gave a partial affirmative answer to this problem via the Cuntz semigroup.
$\mathrm{C}^{*}$
-algebra with the global Glimm property is nowhere scattered (see [Reference Thiel and Vilalta15]). Thiel and Vilalta in [Reference Thiel and Vilalta15, Theorem 7.1] gave a partial affirmative answer to this problem via the Cuntz semigroup.
![]() $(3)$
In [Reference Kirchberg and Rørdam6, Question 4.8], Kirchberg and Rørdam asked whether a
$(3)$
In [Reference Kirchberg and Rørdam6, Question 4.8], Kirchberg and Rørdam asked whether a
![]() $\mathrm{C}^{*}$
-algebra A is purely infinite if and only if every nonzero hereditary
$\mathrm{C}^{*}$
-algebra A is purely infinite if and only if every nonzero hereditary
![]() $\mathrm{C}^{*}$
-subalgebra in every quotient of A contains an infinite positive element (i.e., A is residual (HI); see Definition 2.1).
$\mathrm{C}^{*}$
-subalgebra in every quotient of A contains an infinite positive element (i.e., A is residual (HI); see Definition 2.1).
As one can see, these problems are related to two main properties, namely, the global Glimm property and pure infiniteness. We show that
![]() $\mathrm{C}^{*}$
-algebras with the global Glimm property, in particular, purely infinite
$\mathrm{C}^{*}$
-algebras with the global Glimm property, in particular, purely infinite
![]() $\mathrm{C}^{*}$
-algebras, contain nonzero, square-zero, elements. The next natural question is whether nonzero, square-zero, elements are automatically properly infinite and can be chosen to be full.
$\mathrm{C}^{*}$
-algebras, contain nonzero, square-zero, elements. The next natural question is whether nonzero, square-zero, elements are automatically properly infinite and can be chosen to be full.
In this article, we investigate the following three properties for an arbitrary
![]() $\mathrm{C}^{*}$
-algebra:
$\mathrm{C}^{*}$
-algebra:
-
(i) the existence of nonzero, square-zero, elements in hereditary
 $\mathrm{C}^{*}$
-subalgebras,
$\mathrm{C}^{*}$
-subalgebras, -
(ii) the fullness of nonzero, square-zero, elements in hereditary
 $\mathrm{C}^{*}$
-subalgebras,
$\mathrm{C}^{*}$
-subalgebras, -
(iii) the proper infiniteness of the absolute values of nonzero, square-zero, elements.
Concerning
![]() $\mathrm{(i)}$
, we define the property (HS
$\mathrm{(i)}$
, we define the property (HS
![]() $_0$
) (resp., residual (HS
$_0$
) (resp., residual (HS
![]() $_0$
)) which requires that every nonzero hereditary
$_0$
)) which requires that every nonzero hereditary
![]() $\mathrm{C}^{*}$
-subalgebra (resp., of every quotient) contain a nonzero, square-zero, element (Definition 2.1). We show that property (HS
$\mathrm{C}^{*}$
-subalgebra (resp., of every quotient) contain a nonzero, square-zero, element (Definition 2.1). We show that property (HS
![]() $_0$
) (resp., residual (HS
$_0$
) (resp., residual (HS
![]() $_0$
)) is equivalent to being antiliminary (resp., nowhere scattered).
$_0$
)) is equivalent to being antiliminary (resp., nowhere scattered).
Concerning
![]() $\mathrm{(ii)}$
, we define the weak Glimm property as a generalization of the global Glimm property (Definition 2.3). We show (Proposition F) that the global Glimm property for a Noetherian
$\mathrm{(ii)}$
, we define the weak Glimm property as a generalization of the global Glimm property (Definition 2.3). We show (Proposition F) that the global Glimm property for a Noetherian
![]() $\mathrm{C}^{*}$
-algebra guarantees the existence of full, square-zero, elements in hereditary
$\mathrm{C}^{*}$
-algebra guarantees the existence of full, square-zero, elements in hereditary
![]() $\mathrm{C}^{*}$
-subalgebras. In particular, we show that a weakly purely infinite (resp., nowhere scattered)
$\mathrm{C}^{*}$
-subalgebras. In particular, we show that a weakly purely infinite (resp., nowhere scattered)
![]() $\mathrm{C}^{*}$
-algebra with the weak Glimm property is purely infinite (resp., has the global Glimm property), giving partial affirmative answers to the questions
$\mathrm{C}^{*}$
-algebra with the weak Glimm property is purely infinite (resp., has the global Glimm property), giving partial affirmative answers to the questions
![]() $(1)$
and
$(1)$
and
![]() $(2)$
above.
$(2)$
above.
Finally, assuming
![]() $\mathrm{(iii)}$
together with the weak Glimm property, we show (Theorem A) that the properties of being (weakly, locally) purely infinite, nowhere scattered, residual (HS
$\mathrm{(iii)}$
together with the weak Glimm property, we show (Theorem A) that the properties of being (weakly, locally) purely infinite, nowhere scattered, residual (HS
![]() $_0$
), residual (HS
$_0$
), residual (HS
![]() $_{\text {t}}$
), and residual (HI) are all equivalent to the global Glimm property, which provides partial answers to the problems
$_{\text {t}}$
), and residual (HI) are all equivalent to the global Glimm property, which provides partial answers to the problems
![]() $(1)$
,
$(1)$
,
![]() $(2)$
, and
$(2)$
, and
![]() $(3)$
above.
$(3)$
above.
The first main result of this article is as follows. Recall that a
![]() $\mathrm{C}^{*}$
-algebra is nowhere scattered if none of its quotients contains a minimal nonzero hereditary subalgebra (see [Reference Thiel and Vilalta16, Definition A]). (Definitions of other concepts are given in Section 2.)
$\mathrm{C}^{*}$
-algebra is nowhere scattered if none of its quotients contains a minimal nonzero hereditary subalgebra (see [Reference Thiel and Vilalta16, Definition A]). (Definitions of other concepts are given in Section 2.)
Theorem A For a
![]() $\mathrm{C}^{*}$
-algebra A with the weak Glimm property and such that the absolute value of every nonzero, square-zero, element is properly infinite, the following statements are equivalent:
$\mathrm{C}^{*}$
-algebra A with the weak Glimm property and such that the absolute value of every nonzero, square-zero, element is properly infinite, the following statements are equivalent:
-
(1) A is locally purely infinite,
-
(2) A has residual (HS
 $_t$
),
$_t$
), -
(3) A is nowhere scattered,
-
(4) A has residual (HS
 $_0$
),
$_0$
), -
(5) A has the global Glimm property,
-
(6) A is purely infinite,
-
(7) A is weakly purely infinite,
-
(8) A has residual (HI).
This result has a series of corollaries.
Corollary B For a
![]() $\mathrm{C}^{*}$
-algebra A in which the absolute value of every nonzero, square-zero, element is properly infinite, the following statements are equivalent:
$\mathrm{C}^{*}$
-algebra A in which the absolute value of every nonzero, square-zero, element is properly infinite, the following statements are equivalent:
-
(1) A is purely infinite,
-
(2) A has the global Glimm property,
-
(3) A has the weak Glimm property and residual (HS
 $_t$
),
$_t$
), -
(4) A has the weak Glimm property and residual (HI).
Corollary C For a
![]() $\mathrm{C}^{*}$
-algebra A with the weak Glimm property the following statements are equivalent:
$\mathrm{C}^{*}$
-algebra A with the weak Glimm property the following statements are equivalent:
-
(1) A is purely infinite,
-
(2) A is weakly purely infinite.
Recall that a
![]() $\mathrm{C}^{*}$
-algebra is
$\mathrm{C}^{*}$
-algebra is
![]() $\it {antiliminary}$
if it contains no nonzero, abelian, positive element. Equivalently, a
$\it {antiliminary}$
if it contains no nonzero, abelian, positive element. Equivalently, a
![]() $\mathrm{C}^{*}$
-algebra A is antiliminary if every nonzero hereditary
$\mathrm{C}^{*}$
-algebra A is antiliminary if every nonzero hereditary
![]() $\mathrm{C}^{*}$
-subalgebra of A is noncommutative (see [Reference Blackadar1, Definition IV.1.1.6] and [Reference Pedersen11, p. 191]). A
$\mathrm{C}^{*}$
-subalgebra of A is noncommutative (see [Reference Blackadar1, Definition IV.1.1.6] and [Reference Pedersen11, p. 191]). A
![]() $\mathrm{C}^{*}$
-algebra A is strictly antiliminary if every quotient of A is antiliminary (see [Reference Blanchard and Kirchberg2, Remark 3.2]).
$\mathrm{C}^{*}$
-algebra A is strictly antiliminary if every quotient of A is antiliminary (see [Reference Blanchard and Kirchberg2, Remark 3.2]).
Corollary D For every
![]() $\mathrm{C}^{*}$
-algebra A,
$\mathrm{C}^{*}$
-algebra A,
-
(i) A has property (HS
 $_0$
) if, and only if, it is antiliminary.
$_0$
) if, and only if, it is antiliminary. -
(ii) A has residual (HS
 $_0$
) if, and only if, it is nowhere scattered.
$_0$
) if, and only if, it is nowhere scattered.
Corollary E For every
![]() $\mathrm{C}^{*}$
-algebra A, the following statements are equivalent:
$\mathrm{C}^{*}$
-algebra A, the following statements are equivalent:
-
(1) A has the global Glimm property,
-
(2) A is nowhere scattered and has the weak Glimm property,
-
(3) A is antiliminary and has the weak Glimm property.
A
![]() $\mathrm{C}^{*}$
-algebra A with the global Glimm property is known to be nowhere scattered, and hence no hereditary
$\mathrm{C}^{*}$
-algebra A with the global Glimm property is known to be nowhere scattered, and hence no hereditary
![]() $\mathrm{C}^{*}$
-subalgebra of A admits a finite-dimensional irreducible representation (see [Reference Thiel and Vilalta16, Theorem 3.1]). Recall that a
$\mathrm{C}^{*}$
-subalgebra of A admits a finite-dimensional irreducible representation (see [Reference Thiel and Vilalta16, Theorem 3.1]). Recall that a
![]() $\mathrm{C}^{*}$
-algebra A is Noetherian (resp., Artinian) if it satisfies the ascending (resp., descending) chain condition for (closed two-sided) ideals. Note that being Noetherian (or Artinian) passes to hereditary
$\mathrm{C}^{*}$
-algebra A is Noetherian (resp., Artinian) if it satisfies the ascending (resp., descending) chain condition for (closed two-sided) ideals. Note that being Noetherian (or Artinian) passes to hereditary
![]() $\mathrm{C}^{*}$
-subalgebras and quotients, and is preserved under extensions (see [Reference Rouzbehani, Amini and Asadi13] for details on chain conditions for
$\mathrm{C}^{*}$
-subalgebras and quotients, and is preserved under extensions (see [Reference Rouzbehani, Amini and Asadi13] for details on chain conditions for
![]() $\mathrm{C}^{*}$
-algebras). It’s worth mentioning that Noetherian (and Artinian)
$\mathrm{C}^{*}$
-algebras). It’s worth mentioning that Noetherian (and Artinian)
![]() $\mathrm{C}^{*}$
-algebras are not necessarily separable (for example, consider
$\mathrm{C}^{*}$
-algebras are not necessarily separable (for example, consider
![]() $\mathbb {B}$
, the
$\mathbb {B}$
, the
![]() $\mathrm{C}^{*}$
-algebra of bounded operators on a separable infinite-dimensional Hilbert space). Furthermore, every hereditary
$\mathrm{C}^{*}$
-algebra of bounded operators on a separable infinite-dimensional Hilbert space). Furthermore, every hereditary
![]() $\mathrm{C}^{*}$
-subalgebra of every Noetherian
$\mathrm{C}^{*}$
-subalgebra of every Noetherian
![]() $\mathrm{C}^{*}$
-algebra has a compact primitive spectrum and therefore has a strictly full element (see [Reference Pasnicu and Rouzbehani10, Lemma 2.1]). This helps us to make a connection between the existence of full, square-zero, elements in all hereditary
$\mathrm{C}^{*}$
-algebra has a compact primitive spectrum and therefore has a strictly full element (see [Reference Pasnicu and Rouzbehani10, Lemma 2.1]). This helps us to make a connection between the existence of full, square-zero, elements in all hereditary
![]() $\mathrm{C}^{*}$
-subalgebras of a Noetherian
$\mathrm{C}^{*}$
-subalgebras of a Noetherian
![]() $\mathrm{C}^{*}$
-algebra and the global Glimm property for that
$\mathrm{C}^{*}$
-algebra and the global Glimm property for that
![]() $\mathrm{C}^{*}$
-algebra (see Proposition F). The existence of full, square-zero, elements has considerable implications on the structure of the unitary group of the
$\mathrm{C}^{*}$
-algebra (see Proposition F). The existence of full, square-zero, elements has considerable implications on the structure of the unitary group of the
![]() $\mathrm{C}^{*}$
-algebra (see [Reference Thiel and Vilalta15, p. 4714]).
$\mathrm{C}^{*}$
-algebra (see [Reference Thiel and Vilalta15, p. 4714]).
Proposition F For a Noetherian
![]() $\mathrm{C}^{*}$
-algebra A, the following statements are equivalent:
$\mathrm{C}^{*}$
-algebra A, the following statements are equivalent:
-
(1) A has the global Glimm property,
-
(2) every hereditary
 $\mathrm{C}^{*}$
-subalgebra of A contains a full, square-zero, element.
$\mathrm{C}^{*}$
-subalgebra of A contains a full, square-zero, element.
Corollary G For a
![]() $\mathrm{C}^{*}$
-algebra A which is both Artinian and Noetherian, the following statements are equivalent:
$\mathrm{C}^{*}$
-algebra A which is both Artinian and Noetherian, the following statements are equivalent:
-
(1) A has residual (HS
 $_0$
),
$_0$
), -
(2) A has the global Glimm property.
2 Preliminaries
In this article, by an ideal we always mean a closed two-sided ideal. For an ideal I (resp.,
![]() $\mathrm{C}^{*}$
-subalgebra B) in a
$\mathrm{C}^{*}$
-subalgebra B) in a
![]() $\mathrm{C}^{*}$
-algebra A, we write
$\mathrm{C}^{*}$
-algebra A, we write
![]() $I\unlhd A$
(resp.,
$I\unlhd A$
(resp.,
![]() $B\leq A$
). Also, for a hereditary (resp., and full)
$B\leq A$
). Also, for a hereditary (resp., and full)
![]() $\mathrm{C}^{*}$
-subalgebra B in a
$\mathrm{C}^{*}$
-subalgebra B in a
![]() $\mathrm{C}^{*}$
-algebra A, we write
$\mathrm{C}^{*}$
-algebra A, we write
![]() $B \leq _h A$
(resp.,
$B \leq _h A$
(resp.,
![]() $B \leq _{h,f} A$
). For a subset
$B \leq _{h,f} A$
). For a subset
![]() $S\subseteq A$
,
$S\subseteq A$
,
![]() $\overline {ASA}$
is the ideal generated by S. We simply write
$\overline {ASA}$
is the ideal generated by S. We simply write
![]() $\overline {AaA}$
when
$\overline {AaA}$
when
![]() $S=\{a\}$
. An element
$S=\{a\}$
. An element
![]() $a\in A$
is called
$a\in A$
is called
![]() $\it {full}$
if
$\it {full}$
if
![]() $A=\overline {AaA}$
(see [Reference Blackadar1, p. 91]). An element
$A=\overline {AaA}$
(see [Reference Blackadar1, p. 91]). An element
![]() $a\in A^+$
is
$a\in A^+$
is
![]() $\it {strictly\; full}$
if
$\it {strictly\; full}$
if
![]() $(a-\varepsilon )_{+}$
is full for some (and so for all sufficiently small)
$(a-\varepsilon )_{+}$
is full for some (and so for all sufficiently small)
![]() $\varepsilon>0$
(see [Reference Ortega, Perera and Rørdam8, p. 46]). A positive element a in a
$\varepsilon>0$
(see [Reference Ortega, Perera and Rørdam8, p. 46]). A positive element a in a
![]() $\mathrm{C}^{*}$
-algebra A is
$\mathrm{C}^{*}$
-algebra A is
![]() $\it {abelian}$
if the hereditary
$\it {abelian}$
if the hereditary
![]() $\mathrm{C}^{*}$
-subalgebra
$\mathrm{C}^{*}$
-subalgebra
![]() $\overline {aAa}$
is commutative. A
$\overline {aAa}$
is commutative. A
![]() $\mathrm{C}^{*}$
-algebra is of
$\mathrm{C}^{*}$
-algebra is of
![]() $\it {type \, I}$
if every nonzero quotient contains a nonzero, abelian, positive element. An
$\it {type \, I}$
if every nonzero quotient contains a nonzero, abelian, positive element. An
![]() $\it {ideal}$
-
$\it {ideal}$
-
![]() $\it {quotient}$
of a
$\it {quotient}$
of a
![]() $\mathrm{C}^{*}$
-algebra A is an ideal of a quotient (equivalently, a quotient of an ideal) of A (see [Reference Thiel and Vilalta16]).
$\mathrm{C}^{*}$
-algebra A is an ideal of a quotient (equivalently, a quotient of an ideal) of A (see [Reference Thiel and Vilalta16]).
We denote by
![]() $\mathrm {Prim}(A)$
the set of primitive ideals in a
$\mathrm {Prim}(A)$
the set of primitive ideals in a
![]() $\mathrm{C}^{*}$
-algebra A, the latter being considered as a topological space with the hull-kernel topology (see [Reference Blackadar1]). Throughout this article, the symbols
$\mathrm{C}^{*}$
-algebra A, the latter being considered as a topological space with the hull-kernel topology (see [Reference Blackadar1]). Throughout this article, the symbols
![]() $\otimes $
and
$\otimes $
and
![]() $\sim _M$
are used to denote the minimal tensor product and strong Morita equivalence, respectively. The
$\sim _M$
are used to denote the minimal tensor product and strong Morita equivalence, respectively. The
![]() $\mathrm{C}^{*}$
-algebra of all compact operators on a Hilbert space
$\mathrm{C}^{*}$
-algebra of all compact operators on a Hilbert space
![]() $\mathcal {H}$
is denoted by
$\mathcal {H}$
is denoted by
![]() $\mathcal {K}(\mathcal {H})$
. When
$\mathcal {K}(\mathcal {H})$
. When
![]() $\mathcal {H}$
is separable and infinite-dimensional, we simply write
$\mathcal {H}$
is separable and infinite-dimensional, we simply write
![]() $\mathcal {K}$
for
$\mathcal {K}$
for
![]() $ \mathcal {K}(\mathcal {H})$
.
$ \mathcal {K}(\mathcal {H})$
.
2.1 Purely infinite
 $\mathrm{C}^{*}$
-algebras
$\mathrm{C}^{*}$
-algebras
Given
![]() $a, b \in A^+$
, we say that a is Cuntz subequivalent to b (and write
$a, b \in A^+$
, we say that a is Cuntz subequivalent to b (and write
![]() $ a \precsim b$
), if there is a sequence
$ a \precsim b$
), if there is a sequence
![]() $\{x_k\}_{k=1}^\infty \subseteq A$
such that
$\{x_k\}_{k=1}^\infty \subseteq A$
such that
![]() $x_k^* b x_k \to a$
, in norm. We say that a and b are
$x_k^* b x_k \to a$
, in norm. We say that a and b are
![]() $\it { Cuntz \; equivalent}$
(and write
$\it { Cuntz \; equivalent}$
(and write
![]() $a\sim _{cu} b$
), if
$a\sim _{cu} b$
), if
![]() $ a \precsim b$
and
$ a \precsim b$
and
![]() $ b \precsim a$
(see [Reference Kirchberg and Rørdam6]). A positive element a is called
$ b \precsim a$
(see [Reference Kirchberg and Rørdam6]). A positive element a is called
![]() $\it {infinite}$
if there exists a nonzero, positive element b in A such that
$\it {infinite}$
if there exists a nonzero, positive element b in A such that
![]() $a \oplus b \precsim a\oplus 0$
in
$a \oplus b \precsim a\oplus 0$
in
![]() $\mathbb M_2(A)$
. If a is not infinite, then we say that a is
$\mathbb M_2(A)$
. If a is not infinite, then we say that a is
![]() $\it {finite}$
. If a is nonzero and if
$\it {finite}$
. If a is nonzero and if
![]() $a \oplus a \precsim a\oplus 0$
in
$a \oplus a \precsim a\oplus 0$
in
![]() $\mathbb M_2(A)$
, then a is said to be properly infinite (see [Reference Kirchberg and Rørdam6, Definition 3.2]). A
$\mathbb M_2(A)$
, then a is said to be properly infinite (see [Reference Kirchberg and Rørdam6, Definition 3.2]). A
![]() $\mathrm{C}^{*}$
-algebra A is said to be purely infinite (p.i.) if there are no characters on A, and for every pair of positive elements
$\mathrm{C}^{*}$
-algebra A is said to be purely infinite (p.i.) if there are no characters on A, and for every pair of positive elements
![]() $a, b$
in A, if
$a, b$
in A, if
![]() $a \in \overline {AbA}$
, then
$a \in \overline {AbA}$
, then
![]() $a \precsim b$
(see [Reference Kirchberg and Rørdam6, Definition 4.1]). A
$a \precsim b$
(see [Reference Kirchberg and Rørdam6, Definition 4.1]). A
![]() $\mathrm{C}^{*}$
-algebra A is said to have property
$\mathrm{C}^{*}$
-algebra A is said to have property
![]() $\it {pi}$
-n if the n-fold direct sum
$\it {pi}$
-n if the n-fold direct sum
![]() $a \oplus a \oplus \cdots \oplus a = a \otimes 1_n$
is properly infinite in
$a \oplus a \oplus \cdots \oplus a = a \otimes 1_n$
is properly infinite in
![]() $\mathbb M_n(A)$
, for every nonzero, positive element a in A. If A is pi-n for some n, then A is called weakly purely infinite (w.p.i.) (see [Reference Kirchberg and Rørdam7, Definition 4.3]). A
$\mathbb M_n(A)$
, for every nonzero, positive element a in A. If A is pi-n for some n, then A is called weakly purely infinite (w.p.i.) (see [Reference Kirchberg and Rørdam7, Definition 4.3]). A
![]() $\mathrm{C}^{*}$
-algebra A is strongly purely infinite (s.p.i.) (see [Reference Kirchberg and Rørdam7, Definition 5.1]) if for every
$\mathrm{C}^{*}$
-algebra A is strongly purely infinite (s.p.i.) (see [Reference Kirchberg and Rørdam7, Definition 5.1]) if for every
 $$ \begin{align*}\begin{pmatrix} a & x^*\\ x & b \end{pmatrix}\in \mathbb M_2(A)^{+}\end{align*} $$
$$ \begin{align*}\begin{pmatrix} a & x^*\\ x & b \end{pmatrix}\in \mathbb M_2(A)^{+}\end{align*} $$
and every
![]() $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
![]() $a_1,a_2\in A$
such that
$a_1,a_2\in A$
such that
 $$ \begin{align*}\left\|\begin{pmatrix} a_1^* & 0\\ 0 & a_2^* \end{pmatrix}\begin{pmatrix} a & x^*\\ x & b \end{pmatrix}\begin{pmatrix} a_1 & 0\\ 0 & a_2 \end{pmatrix}-\begin{pmatrix} a & 0\\ 0 & b \end{pmatrix}\right\|<\varepsilon.\end{align*} $$
$$ \begin{align*}\left\|\begin{pmatrix} a_1^* & 0\\ 0 & a_2^* \end{pmatrix}\begin{pmatrix} a & x^*\\ x & b \end{pmatrix}\begin{pmatrix} a_1 & 0\\ 0 & a_2 \end{pmatrix}-\begin{pmatrix} a & 0\\ 0 & b \end{pmatrix}\right\|<\varepsilon.\end{align*} $$
A
![]() $\mathrm{C}^{*}$
-algebra A is said to be
$\mathrm{C}^{*}$
-algebra A is said to be
![]() $\it {locally\; purely\; infinite}$
(l.p.i.) if for every primitive ideal J of A and every element
$\it {locally\; purely\; infinite}$
(l.p.i.) if for every primitive ideal J of A and every element
![]() $b\in A^+$
with
$b\in A^+$
with
![]() $\| b+ J\|>0$
, there is a nonzero, stable,
$\| b+ J\|>0$
, there is a nonzero, stable,
![]() $\mathrm{C}^{*}$
-subalgebra D of the hereditary
$\mathrm{C}^{*}$
-subalgebra D of the hereditary
![]() $\mathrm{C}^{*}$
-subalgebra generated by b such that D is not included in J [Reference Blanchard and Kirchberg2, Definition 1.3].
$\mathrm{C}^{*}$
-subalgebra generated by b such that D is not included in J [Reference Blanchard and Kirchberg2, Definition 1.3].
2.2 Square-zero elements in a
 $\mathrm{C}^{*}$
-algebra
$\mathrm{C}^{*}$
-algebra
An element r in a
![]() $\mathrm{C}^{*}$
-algebra will be called
$\mathrm{C}^{*}$
-algebra will be called
![]() $\it {square}$
-
$\it {square}$
-
![]() $\it {zero}$
if
$\it {zero}$
if
![]() $r^2=0$
(see [Reference Thiel and Vilalta15]). We denote by
$r^2=0$
(see [Reference Thiel and Vilalta15]). We denote by
![]() $S_0(A)$
the set of all square-zero elements in the
$S_0(A)$
the set of all square-zero elements in the
![]() $\mathrm{C}^{*}$
-algebra A. The existence of nonzero, square-zero, elements implies that the underlying
$\mathrm{C}^{*}$
-algebra A. The existence of nonzero, square-zero, elements implies that the underlying
![]() $\mathrm{C}^{*}$
-algebra is noncommutative (see [Reference Enders and Shulman4, Corollary 5]). These elements also play the role of generators for a large class of noncommutative
$\mathrm{C}^{*}$
-algebra is noncommutative (see [Reference Enders and Shulman4, Corollary 5]). These elements also play the role of generators for a large class of noncommutative
![]() $\mathrm{C}^{*}$
-algebras. To be more explicit, for a unital
$\mathrm{C}^{*}$
-algebras. To be more explicit, for a unital
![]() $\mathrm{C}^{*}$
-algebra A, denote by
$\mathrm{C}^{*}$
-algebra A, denote by
![]() $\mathrm {Inv}(A)$
the set of all invertible elements in A, and set
$\mathrm {Inv}(A)$
the set of all invertible elements in A, and set
![]() $1-S_0(A):=\{ 1-r \; | \; r \in S_0(A) \}.$
Then the following assertions hold:
$1-S_0(A):=\{ 1-r \; | \; r \in S_0(A) \}.$
Then the following assertions hold:
-
(i) If A is noncommutative, then
 $$ \begin{align*}(1-S_0(A))^*=(1-S_0(A))^{-1}=1-S_0(A)\subseteq \mathrm{Inv}(A).\end{align*} $$
$$ \begin{align*}(1-S_0(A))^*=(1-S_0(A))^{-1}=1-S_0(A)\subseteq \mathrm{Inv}(A).\end{align*} $$
-
(ii) If A has no one-dimensional irreducible representation, then
 $$ \begin{align*}C^*(1-S_0(A))= A.\end{align*} $$
$$ \begin{align*}C^*(1-S_0(A))= A.\end{align*} $$
To see
![]() $\mathrm{(i)}$
, note that, for every
$\mathrm{(i)}$
, note that, for every
![]() $r \in S_0(A)$
,
$r \in S_0(A)$
,
and hence every element of
![]() $1-S_0(A)$
is invertible, and
$1-S_0(A)$
is invertible, and
![]() $(1-r)^{-1} = (1+r)$
. Moreover, for every
$(1-r)^{-1} = (1+r)$
. Moreover, for every
![]() $r \in S_0(A)$
,
$r \in S_0(A)$
,
![]() $(r^*)^2=(r^2)^*=0,$
and so
$(r^*)^2=(r^2)^*=0,$
and so
![]() $(1-r)^*=1-r^* \in 1-S_0(A).$
Therefore, the sets
$(1-r)^*=1-r^* \in 1-S_0(A).$
Therefore, the sets
![]() $(1-S_0(A))^*$
,
$(1-S_0(A))^*$
,
![]() $(1-S_0(A))^{-1}$
and
$(1-S_0(A))^{-1}$
and
![]() $1-S_0(A)$
coincide.
$1-S_0(A)$
coincide.
Next, let us prove
![]() $\mathrm{(ii)}$
. For every
$\mathrm{(ii)}$
. For every
![]() $r \in S_0(A)$
, we have
$r \in S_0(A)$
, we have
that is,
![]() $S_0(A) \subseteq \mathrm {span}(1-S_0(A)).$
By [Reference Gardella and Thiel5, Theorem 4.3] and [Reference Robert12, Theorems 1.3 and 4.2], we have, by the hypothesis on A,
$S_0(A) \subseteq \mathrm {span}(1-S_0(A)).$
By [Reference Gardella and Thiel5, Theorem 4.3] and [Reference Robert12, Theorems 1.3 and 4.2], we have, by the hypothesis on A,
where
![]() $[A, A]$
is the set of all commutators in A. Thus,
$[A, A]$
is the set of all commutators in A. Thus,
![]() $C^*(1-S_0(A))= A,$
as claimed.
$C^*(1-S_0(A))= A,$
as claimed.
Note that though both sets
![]() $S_0(A)$
and
$S_0(A)$
and
![]() $1-S_0(A)$
generate A as a
$1-S_0(A)$
generate A as a
![]() $\mathrm{C}^{*}$
-algebra, while
$\mathrm{C}^{*}$
-algebra, while
![]() $(1-S_0(A))\subseteq \mathrm {Inv}(A)$
we only have
$(1-S_0(A))\subseteq \mathrm {Inv}(A)$
we only have
![]() $S_0(A)\subseteq \overline {\mathrm {Inv}(A)}.$
Indeed, if r is a square-zero element of A, then its spectral radius is zero and
$S_0(A)\subseteq \overline {\mathrm {Inv}(A)}.$
Indeed, if r is a square-zero element of A, then its spectral radius is zero and
2.3 The weak Glimm property
In this section, we define the property (HS
![]() $_0$
) and the weak Glimm property for
$_0$
) and the weak Glimm property for
![]() $\mathrm{C}^{*}$
-algebras. Everywhere, A is an arbitrary
$\mathrm{C}^{*}$
-algebras. Everywhere, A is an arbitrary
![]() $\mathrm{C}^{*}$
-algebra.
$\mathrm{C}^{*}$
-algebra.
Definition 2.1
![]() $\mathrm{(i)}\ A$
is said to have property
$\mathrm{(i)}\ A$
is said to have property
![]() $(HS_0)$
(resp.,
$(HS_0)$
(resp.,
![]() $(HI)$
) if every nonzero hereditary
$(HI)$
) if every nonzero hereditary
![]() $\mathrm{C}^{*}$
-subalgebra of A contains a nonzero, square-zero (resp., infinite) element.
$\mathrm{C}^{*}$
-subalgebra of A contains a nonzero, square-zero (resp., infinite) element.
![]() $\mathrm{(ii)}\ A$
is said to have residual
$\mathrm{(ii)}\ A$
is said to have residual
![]() $(HS_0)$
(resp., residual
$(HS_0)$
(resp., residual
![]() $(HI)$
) if every quotient of A has property (HS
$(HI)$
) if every quotient of A has property (HS
![]() $_0$
) (resp., (HI)).
$_0$
) (resp., (HI)).
Definition 2.2
![]() $\mathrm{(i)}\ A$
is said to have property
$\mathrm{(i)}\ A$
is said to have property
![]() $(HS_t)$
if every nonzero hereditary
$(HS_t)$
if every nonzero hereditary
![]() $\mathrm{C}^{*}$
-subalgebra of A contains a nonzero, stable,
$\mathrm{C}^{*}$
-subalgebra of A contains a nonzero, stable,
![]() $\mathrm{C}^{*}$
-subalgebra.
$\mathrm{C}^{*}$
-subalgebra.
![]() $\mathrm{(ii)}\ A$
is said to have residual
$\mathrm{(ii)}\ A$
is said to have residual
![]() $(HS_t)$
if every quotient of A has property (HS
$(HS_t)$
if every quotient of A has property (HS
![]() $_{\text {t}}$
).
$_{\text {t}}$
).
Remark 2.1 Define
![]() $\mathcal {C}_1$
(resp.,
$\mathcal {C}_1$
(resp.,
![]() $\mathcal {C}_2$
, and
$\mathcal {C}_2$
, and
![]() $\mathcal {C}_3$
) to be the class of all
$\mathcal {C}_3$
) to be the class of all
![]() $\mathrm{C}^{*}$
-algebras which have a nonzero, square-zero, element (resp., an infinite element, a nonzero, stable,
$\mathrm{C}^{*}$
-algebras which have a nonzero, square-zero, element (resp., an infinite element, a nonzero, stable,
![]() $\mathrm{C}^{*}$
-subalgebra). These classes are upwards directed. We recall that a class
$\mathrm{C}^{*}$
-subalgebra). These classes are upwards directed. We recall that a class
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathrm{C}^{*}$
-algebras is called upwards directed (or upwards hereditary) if whenever A is a
$\mathrm{C}^{*}$
-algebras is called upwards directed (or upwards hereditary) if whenever A is a
![]() $\mathrm{C}^{*}$
-algebra which contains a
$\mathrm{C}^{*}$
-algebra which contains a
![]() $\mathrm{C}^{*}$
-subalgebra isomorphic to a
$\mathrm{C}^{*}$
-subalgebra isomorphic to a
![]() $\mathrm{C}^{*}$
-algebra in
$\mathrm{C}^{*}$
-algebra in
![]() $\mathcal {C}$
, then
$\mathcal {C}$
, then
![]() $A \in \mathcal {C}$
(see [Reference Pasnicu and Phillips9, Definition 5.1]). By [Reference Pasnicu and Phillips9, Definition 5.2], and Definitions 2.1 and 2.2 above,
$A \in \mathcal {C}$
(see [Reference Pasnicu and Phillips9, Definition 5.1]). By [Reference Pasnicu and Phillips9, Definition 5.2], and Definitions 2.1 and 2.2 above,
![]() $\mathrm{(i)}\ A$
has property (HS
$\mathrm{(i)}\ A$
has property (HS
![]() $_0$
) (resp., (HI), or (HS
$_0$
) (resp., (HI), or (HS
![]() $_{\text {t}}$
)) if and only if all hereditary subalgebras belong to
$_{\text {t}}$
)) if and only if all hereditary subalgebras belong to
![]() $\mathcal {C}_1$
(resp.,
$\mathcal {C}_1$
(resp.,
![]() $\mathcal {C}_2$
, or
$\mathcal {C}_2$
, or
![]() $\mathcal {C}_3$
), and
$\mathcal {C}_3$
), and
![]() $\mathrm{(ii)}\ A$
has residual (HS
$\mathrm{(ii)}\ A$
has residual (HS
![]() $_0$
) (resp., residual (HI), or residual (HS
$_0$
) (resp., residual (HI), or residual (HS
![]() $_{\text {t}}$
)) if and only if quotients of hereditary subalgebras belong to
$_{\text {t}}$
)) if and only if quotients of hereditary subalgebras belong to
![]() $\mathcal {C}_1$
(resp.,
$\mathcal {C}_1$
(resp.,
![]() $\mathcal {C}_2$
, or
$\mathcal {C}_2$
, or
![]() $\mathcal {C}_3$
).
$\mathcal {C}_3$
).
We can use the permanence results of Section 5 of [Reference Pasnicu and Phillips9] to obtain the following permanence properties:
![]() $(1)$
The properties (HS
$(1)$
The properties (HS
![]() $_0$
), (HI), (HS
$_0$
), (HI), (HS
![]() $_{\text {t}}$
), residual (HS
$_{\text {t}}$
), residual (HS
![]() $_0$
), residual (HI), and residual (HS
$_0$
), residual (HI), and residual (HS
![]() $_{\text {t}}$
) are preserved under:
$_{\text {t}}$
) are preserved under:
-
(i) passage to hereditary
 $\mathrm{C}^{*}$
-subalgebras (see [Reference Pasnicu and Phillips9, Proposition 5.10]),
$\mathrm{C}^{*}$
-subalgebras (see [Reference Pasnicu and Phillips9, Proposition 5.10]), -
(ii) strong Morita equivalence for separable
 $\mathrm{C}^{*}$
-algebras (see [Reference Pasnicu and Phillips9, Corollary 5.13]),
$\mathrm{C}^{*}$
-algebras (see [Reference Pasnicu and Phillips9, Corollary 5.13]), -
(iii) direct limits of separable
 $\mathrm{C}^{*}$
-algebras (see [Reference Pasnicu and Phillips9, Proposition 5.9]),
$\mathrm{C}^{*}$
-algebras (see [Reference Pasnicu and Phillips9, Proposition 5.9]), -
(iv) crossed products by arbitrary actions of
 $\mathbb {Z}_2$
(see [Reference Pasnicu and Phillips9, Corollary 5.6]),
$\mathbb {Z}_2$
(see [Reference Pasnicu and Phillips9, Corollary 5.6]), -
(v) crossed products by Rokhlin actions of
 $\mathbb {Z}$
on unital
$\mathbb {Z}$
on unital
 $\mathrm{C}^{*}$
-algebras (see [Reference Pasnicu and Phillips9, Corollary 5.4]).
$\mathrm{C}^{*}$
-algebras (see [Reference Pasnicu and Phillips9, Corollary 5.4]).
![]() $(2)$
For an ideal
$(2)$
For an ideal
![]() $I\unlhd A$
, A has residual (HS
$I\unlhd A$
, A has residual (HS
![]() $_0$
) (resp., residual (HI), or residual (HS
$_0$
) (resp., residual (HI), or residual (HS
![]() $_{\text {t}}$
)) if and only if both I and
$_{\text {t}}$
)) if and only if both I and
![]() $A/I$
do (see [Reference Pasnicu and Phillips9, Proposition 5.8]).
$A/I$
do (see [Reference Pasnicu and Phillips9, Proposition 5.8]).
![]() $(3)$
A has property (HS
$(3)$
A has property (HS
![]() $_0$
) (resp., property (HI), property (HS
$_0$
) (resp., property (HI), property (HS
![]() $_{\text {t}}$
), residual (HS
$_{\text {t}}$
), residual (HS
![]() $_0$
), residual (HI), or residual (HS
$_0$
), residual (HI), or residual (HS
![]() $_{\text {t}}$
)) if and only if
$_{\text {t}}$
)) if and only if
![]() $A\otimes \mathcal {K}$
or
$A\otimes \mathcal {K}$
or
![]() $\mathbb M_n(A)$
do, for some (all)
$\mathbb M_n(A)$
do, for some (all)
![]() $n\geq 1$
(see [Reference Pasnicu and Phillips9, Propositions 5.11 and 5.12]).
$n\geq 1$
(see [Reference Pasnicu and Phillips9, Propositions 5.11 and 5.12]).
A
![]() $\mathrm{C}^{*}$
-algebra A is said to have the global Glimm property if for each natural number n, for each positive element a in A, and for each
$\mathrm{C}^{*}$
-algebra A is said to have the global Glimm property if for each natural number n, for each positive element a in A, and for each
![]() $\varepsilon> 0$
there is a
$\varepsilon> 0$
there is a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\varphi : \mathbb M_n(C_0((0, 1])) \to \overline {aAa}$
such that
$\varphi : \mathbb M_n(C_0((0, 1])) \to \overline {aAa}$
such that
![]() $(a- \varepsilon )_+$
belongs to the ideal of A generated by the image of
$(a- \varepsilon )_+$
belongs to the ideal of A generated by the image of
![]() $\varphi $
(see [Reference Kirchberg and Rørdam7, Definition 4.12]); or, equivalently, if, for every
$\varphi $
(see [Reference Kirchberg and Rørdam7, Definition 4.12]); or, equivalently, if, for every
![]() $a\in A^+$
and
$a\in A^+$
and
![]() $\varepsilon> 0$
there exists an element
$\varepsilon> 0$
there exists an element
![]() $r \in \overline {aAa}$
with
$r \in \overline {aAa}$
with
![]() $r^2 = 0$
such that
$r^2 = 0$
such that
![]() $(a - \varepsilon )_+ \in \overline {ArA}$
(see [Reference Thiel and Vilalta15, Theorem 3.6(
$(a - \varepsilon )_+ \in \overline {ArA}$
(see [Reference Thiel and Vilalta15, Theorem 3.6(
![]() $(1)\iff (3)$
)]).
$(1)\iff (3)$
)]).
Definition 2.3 A
![]() $\mathrm{C}^{*}$
-algebra A will be said to have the weak Glimm property, if for every
$\mathrm{C}^{*}$
-algebra A will be said to have the weak Glimm property, if for every
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $a\in A^+$
with
$a\in A^+$
with
![]() $\{0\} \neq S_0(\overline {aAa})$
, there exists
$\{0\} \neq S_0(\overline {aAa})$
, there exists
![]() $r\in S_0(\overline {aAa})$
such that
$r\in S_0(\overline {aAa})$
such that
![]() $(a - \varepsilon )_+ \in \overline {ArA}$
.
$(a - \varepsilon )_+ \in \overline {ArA}$
.
Clearly, the global Glimm property implies the weak Glimm property. The converse is not necessarily true, even for simple
![]() $\mathrm{C}^{*}$
-algebras. For example, the
$\mathrm{C}^{*}$
-algebras. For example, the
![]() $\mathrm{C}^{*}$
-algebras
$\mathrm{C}^{*}$
-algebras
![]() $A=\Bbb C$
and
$A=\Bbb C$
and
![]() $B= \Bbb C \oplus \mathcal {O}_n$
, for the Cuntz algebra
$B= \Bbb C \oplus \mathcal {O}_n$
, for the Cuntz algebra
![]() $\mathcal {O}_n$
with
$\mathcal {O}_n$
with
![]() $2\leq n\leq \infty $
, have the weak Glimm property, but not the global Glimm property (
$2\leq n\leq \infty $
, have the weak Glimm property, but not the global Glimm property (
![]() $\Bbb C$
has no nonzero, square-zero, element).
$\Bbb C$
has no nonzero, square-zero, element).
3 Proofs of the main results
Proof of Theorem A
First, note that we use the assumption “the weak Glimm property” only to prove the implication
![]() $(4) \Rightarrow (5)$
below, and the assumption “the absolute value of every nonzero, square-zero, element is properly infinite” only to prove the implication
$(4) \Rightarrow (5)$
below, and the assumption “the absolute value of every nonzero, square-zero, element is properly infinite” only to prove the implication
![]() $(5) \Rightarrow (6)$
below.
$(5) \Rightarrow (6)$
below.
![]() $(1) \Rightarrow (2)$
: Let Q be a quotient of A, and let
$(1) \Rightarrow (2)$
: Let Q be a quotient of A, and let
![]() $0\neq H\leq _h Q$
. Since local pure infiniteness passes to hereditary
$0\neq H\leq _h Q$
. Since local pure infiniteness passes to hereditary
![]() $\mathrm{C}^{*}$
-subalgebras and quotients (see [Reference Blanchard and Kirchberg2, Proposition 4.1(iii)]), H is locally purely infinite. In particular, H contains a nonzero, stable,
$\mathrm{C}^{*}$
-subalgebras and quotients (see [Reference Blanchard and Kirchberg2, Proposition 4.1(iii)]), H is locally purely infinite. In particular, H contains a nonzero, stable,
![]() $\mathrm{C}^{*}$
-subalgebra D, as desired. (D may be chosen to be nonzero in any specified primitive quotient of H.)
$\mathrm{C}^{*}$
-subalgebra D, as desired. (D may be chosen to be nonzero in any specified primitive quotient of H.)
![]() $(2) \Rightarrow (3)$
: Suppose that A is not nowhere scattered. Then [Reference Thiel and Vilalta16, Theorem 3.1(
$(2) \Rightarrow (3)$
: Suppose that A is not nowhere scattered. Then [Reference Thiel and Vilalta16, Theorem 3.1(
![]() $(1)\iff (6)$
)] implies that A has a GCR irreducible representation, say
$(1)\iff (6)$
)] implies that A has a GCR irreducible representation, say
![]() $\pi : A \to \mathcal {B}(\mathcal {H})$
. Thus,
$\pi : A \to \mathcal {B}(\mathcal {H})$
. Thus,
![]() $\mathcal {K}(\mathcal {H}) \cap \pi (A) \neq \{0\}$
, and in fact
$\mathcal {K}(\mathcal {H}) \cap \pi (A) \neq \{0\}$
, and in fact
![]() $\mathcal {K}(\mathcal {H}) \subseteq \pi (A)$
, so
$\mathcal {K}(\mathcal {H}) \subseteq \pi (A)$
, so
Since by hypothesis A has residual (HS
![]() $_{\text {t}}$
), and (by Remark 2.1) residual (HS
$_{\text {t}}$
), and (by Remark 2.1) residual (HS
![]() $_{\text {t}}$
) passes to ideals and quotients,
$_{\text {t}}$
) passes to ideals and quotients,
![]() $\mathcal {K}(\mathcal {H})$
has property (HS
$\mathcal {K}(\mathcal {H})$
has property (HS
![]() $_{\text {t}}$
). By [Reference Blanchard and Kirchberg2, Proposition 3.1], a simple
$_{\text {t}}$
). By [Reference Blanchard and Kirchberg2, Proposition 3.1], a simple
![]() $\mathrm{C}^{*}$
-algebra such that every nonzero hereditary
$\mathrm{C}^{*}$
-algebra such that every nonzero hereditary
![]() $\mathrm{C}^{*}$
-subalgebra contains a nonzero, stable,
$\mathrm{C}^{*}$
-subalgebra contains a nonzero, stable,
![]() $\mathrm{C}^{*}$
-subalgebra must be purely infinite. This is a contradiction since
$\mathrm{C}^{*}$
-subalgebra must be purely infinite. This is a contradiction since
![]() $\mathcal {K}(\mathcal {H})$
is simple and elementary, and so is of type I [Reference Blackadar1, Corollary IV.1.2.6], and no
$\mathcal {K}(\mathcal {H})$
is simple and elementary, and so is of type I [Reference Blackadar1, Corollary IV.1.2.6], and no
![]() $\mathrm{C}^{*}$
-algebra of type I is purely infinite (see [Reference Kirchberg and Rørdam6, Proposition 4.4]).
$\mathrm{C}^{*}$
-algebra of type I is purely infinite (see [Reference Kirchberg and Rørdam6, Proposition 4.4]).
![]() $(3) \Rightarrow (4)$
: Let Q be a quotient of A, and let
$(3) \Rightarrow (4)$
: Let Q be a quotient of A, and let
![]() $0\neq H\leq _h Q$
. Note that the property of being nowhere scattered passes to hereditary
$0\neq H\leq _h Q$
. Note that the property of being nowhere scattered passes to hereditary
![]() $\mathrm{C}^{*}$
-subalgebras and quotients (by [Reference Thiel and Vilalta16, Proposition 4.1]). Since H is nowhere scattered, it is not of type I (see [Reference Thiel and Vilalta16, Theorem 3.1(
$\mathrm{C}^{*}$
-subalgebras and quotients (by [Reference Thiel and Vilalta16, Proposition 4.1]). Since H is nowhere scattered, it is not of type I (see [Reference Thiel and Vilalta16, Theorem 3.1(
![]() $(1)\iff (3)$
)]), and so is noncommutative [Reference Blackadar1, Section IV.1.1.4]. But every noncommutative
$(1)\iff (3)$
)]), and so is noncommutative [Reference Blackadar1, Section IV.1.1.4]. But every noncommutative
![]() $\mathrm{C}^{*}$
-algebra has a nonzero, square-zero, element (Proposition II.6.4.14 of [Reference Blackadar1]). This shows that A has residual (HS
$\mathrm{C}^{*}$
-algebra has a nonzero, square-zero, element (Proposition II.6.4.14 of [Reference Blackadar1]). This shows that A has residual (HS
![]() $_0$
).
$_0$
).
![]() $(4) \Rightarrow (5)$
: Suppose that A has residual (HS
$(4) \Rightarrow (5)$
: Suppose that A has residual (HS
![]() $_0$
),
$_0$
),
![]() $0\neq a\in A^+$
, and
$0\neq a\in A^+$
, and
![]() $\varepsilon> 0$
. Then
$\varepsilon> 0$
. Then
![]() $\overline {aAa}$
has a nonzero, square-zero, element. By the weak Glimm property, there is
$\overline {aAa}$
has a nonzero, square-zero, element. By the weak Glimm property, there is
![]() $r \in \overline {aAa}$
with
$r \in \overline {aAa}$
with
![]() $r^2=0$
and
$r^2=0$
and
![]() $(a-\varepsilon )_+\in \overline {ArA}$
. Thus A has the global Glimm property.
$(a-\varepsilon )_+\in \overline {ArA}$
. Thus A has the global Glimm property.
![]() $(5) \Rightarrow (6)$
: Let
$(5) \Rightarrow (6)$
: Let
![]() $0\neq a \in A^+$
and
$0\neq a \in A^+$
and
![]() $\varepsilon>0$
. Since A has the global Glimm property, there is
$\varepsilon>0$
. Since A has the global Glimm property, there is
![]() $r \in S_0(\overline {aAa})$
with
$r \in S_0(\overline {aAa})$
with
![]() $(a-\varepsilon )_+ \in \overline {ArA}$
. Since
$(a-\varepsilon )_+ \in \overline {ArA}$
. Since
![]() $|r|\sim _{cu} rr^* \sim _{cu} r^*r,$
the orthogonal elements
$|r|\sim _{cu} rr^* \sim _{cu} r^*r,$
the orthogonal elements
![]() $x_1:= rr^*$
and
$x_1:= rr^*$
and
![]() $x_2:= r^*r$
are properly infinite, because, by hypothesis,
$x_2:= r^*r$
are properly infinite, because, by hypothesis,
![]() $|r|$
is properly infinite. On the other hand, we have that
$|r|$
is properly infinite. On the other hand, we have that
and hence,
![]() $ (a-\varepsilon )_+ \precsim x_1$
and
$ (a-\varepsilon )_+ \precsim x_1$
and
![]() $(a-\varepsilon )_+ \precsim x_2,$
by [Reference Kirchberg and Rørdam6, Proposition 3.5(ii)]. Now, [Reference Kirchberg and Rørdam6, Proposition 3.3(
$(a-\varepsilon )_+ \precsim x_2,$
by [Reference Kirchberg and Rørdam6, Proposition 3.5(ii)]. Now, [Reference Kirchberg and Rørdam6, Proposition 3.3(
![]() $\mathrm{(i)}\iff \mathrm{(iii)}$
)] implies that a is properly infinite. This shows that A is purely infinite (see [Reference Kirchberg and Rørdam6, Lemma 4.2]).
$\mathrm{(i)}\iff \mathrm{(iii)}$
)] implies that a is properly infinite. This shows that A is purely infinite (see [Reference Kirchberg and Rørdam6, Lemma 4.2]).
![]() $(6) \Rightarrow (1)$
, and
$(6) \Rightarrow (1)$
, and
![]() $ (6) \Rightarrow (7)$
: These implications are known (see [Reference Blanchard and Kirchberg2, p. 465] and [Reference Kirchberg and Rørdam7, Definition 4.1]).
$ (6) \Rightarrow (7)$
: These implications are known (see [Reference Blanchard and Kirchberg2, p. 465] and [Reference Kirchberg and Rørdam7, Definition 4.1]).
![]() $(7) \Rightarrow (8)$
: Let A be a weakly purely infinite
$(7) \Rightarrow (8)$
: Let A be a weakly purely infinite
![]() $\mathrm{C}^{*}$
-algebra, Q be a quotient of A, and
$\mathrm{C}^{*}$
-algebra, Q be a quotient of A, and
![]() $H\leq _h Q$
. Then H is weakly purely infinite, and hence pi-n for some
$H\leq _h Q$
. Then H is weakly purely infinite, and hence pi-n for some
![]() $n\in \Bbb N$
, because being weakly purely infinite passes to hereditary
$n\in \Bbb N$
, because being weakly purely infinite passes to hereditary
![]() $\mathrm{C}^{*}$
-subalgebras and quotients (see [Reference Kirchberg and Rørdam7, Definition 4.3 and Proposition 4.5(ii) and (iii)]). Since H has no nonzero finite-dimensional representation, Glimm’s lemma [Reference Kirchberg and Rørdam6, Proposition 4.10] implies the existence of nonzero, pairwise orthogonal, pairwise equivalent, positive, elements
$\mathrm{C}^{*}$
-subalgebras and quotients (see [Reference Kirchberg and Rørdam7, Definition 4.3 and Proposition 4.5(ii) and (iii)]). Since H has no nonzero finite-dimensional representation, Glimm’s lemma [Reference Kirchberg and Rørdam6, Proposition 4.10] implies the existence of nonzero, pairwise orthogonal, pairwise equivalent, positive, elements
![]() $t_1, t_2, \dots , t_n$
in H. By [Reference Kirchberg and Rørdam6, Lemmas 2.8 and 2.9],
$t_1, t_2, \dots , t_n$
in H. By [Reference Kirchberg and Rørdam6, Lemmas 2.8 and 2.9],
 $$ \begin{align*}t_1 \otimes 1_n \sim t_1 \oplus t_2 \oplus \cdots \oplus t_n\sim \sum_{i=1}^{n} t_i.\end{align*} $$
$$ \begin{align*}t_1 \otimes 1_n \sim t_1 \oplus t_2 \oplus \cdots \oplus t_n\sim \sum_{i=1}^{n} t_i.\end{align*} $$
Since H is pi-n, the element
![]() $ t_1 \otimes 1_n$
is properly infinite in
$ t_1 \otimes 1_n$
is properly infinite in
![]() $\mathbb M_n(H)$
. But for
$\mathbb M_n(H)$
. But for
![]() $x:= \sum _{i=1}^{n} t_i\in H,\ x \sim t_1 \otimes 1_n.$
Thus x is properly infinite in H.
$x:= \sum _{i=1}^{n} t_i\in H,\ x \sim t_1 \otimes 1_n.$
Thus x is properly infinite in H.
![]() $(8) \Rightarrow (3)$
: Assume that A is not nowhere scattered. Then A has a nonzero elementary ideal-quotient, say L (see [Reference Thiel and Vilalta16, Theorem 3.1(
$(8) \Rightarrow (3)$
: Assume that A is not nowhere scattered. Then A has a nonzero elementary ideal-quotient, say L (see [Reference Thiel and Vilalta16, Theorem 3.1(
![]() $(1)\iff (5)$
)]). In particular, L is a simple
$(1)\iff (5)$
)]). In particular, L is a simple
![]() $\mathrm{C}^{*}$
-algebra [Reference Blackadar1, Definition IV.1.2.1]. Since residual (HI) passes to ideals and quotients (by Remark 2.1), the
$\mathrm{C}^{*}$
-algebra [Reference Blackadar1, Definition IV.1.2.1]. Since residual (HI) passes to ideals and quotients (by Remark 2.1), the
![]() $\mathrm{C}^{*}$
-algebra L has residual (HI). Let
$\mathrm{C}^{*}$
-algebra L has residual (HI). Let
![]() $0\neq a \in L^+$
and
$0\neq a \in L^+$
and
![]() $L_a:=\overline {aLa}$
. Since L has residual (HI), there is a properly infinite element x in
$L_a:=\overline {aLa}$
. Since L has residual (HI), there is a properly infinite element x in
![]() $L_a$
. But, we have that
$L_a$
. But, we have that
![]() $x \precsim a$
and
$x \precsim a$
and
![]() $a \in L_a = \overline {L_axL_a}.$
Therefore, by [Reference Kirchberg and Rørdam6, Lemma 3.8], a is properly infinite in
$a \in L_a = \overline {L_axL_a}.$
Therefore, by [Reference Kirchberg and Rørdam6, Lemma 3.8], a is properly infinite in
![]() $L_a$
, and so in L. Hence L is purely infinite (by [Reference Kirchberg and Rørdam6, Lemma 4.2]), which is a contradiction, as L is of type I (see [Reference Kirchberg and Rørdam6, Proposition 4.4]).
$L_a$
, and so in L. Hence L is purely infinite (by [Reference Kirchberg and Rørdam6, Lemma 4.2]), which is a contradiction, as L is of type I (see [Reference Kirchberg and Rørdam6, Proposition 4.4]).
Remark 3.1 As shown in the proof of Theorem A, for every
![]() $\mathrm{C}^{*}$
-algebra A (without any extra assumption),
$\mathrm{C}^{*}$
-algebra A (without any extra assumption),
![]() $ (1) \Rightarrow (2) \Rightarrow (3) \Rightarrow (4).$
Moreover, it is known that
$ (1) \Rightarrow (2) \Rightarrow (3) \Rightarrow (4).$
Moreover, it is known that
![]() $\mbox {s.p.i.} \Rightarrow \mbox {p.i.} \Rightarrow \mbox {w.p.i.} \Rightarrow \mbox {l.p.i.}$
(see [Reference Blanchard and Kirchberg2, Reference Kirchberg and Rørdam7]). Therefore, the inclusions in Figure 1 are confirmed. Note that antiliminary (and nowhere scattered)
$\mbox {s.p.i.} \Rightarrow \mbox {p.i.} \Rightarrow \mbox {w.p.i.} \Rightarrow \mbox {l.p.i.}$
(see [Reference Blanchard and Kirchberg2, Reference Kirchberg and Rørdam7]). Therefore, the inclusions in Figure 1 are confirmed. Note that antiliminary (and nowhere scattered)
![]() $\mathrm{C}^{*}$
-algebras are not necessarily purely infinite. For example, let
$\mathrm{C}^{*}$
-algebras are not necessarily purely infinite. For example, let
![]() $A_\infty $
be the universal Glimm algebra (see [Reference Pedersen11, Section 6.4.2]), and let
$A_\infty $
be the universal Glimm algebra (see [Reference Pedersen11, Section 6.4.2]), and let
![]() $\mathcal {Z}$
be the Jiang-Su algebra (see [Reference Rørdam14]). Then
$\mathcal {Z}$
be the Jiang-Su algebra (see [Reference Rørdam14]). Then
![]() $A_\infty $
is a simple, unital AF-algebra which is antiliminary (see [Reference Pedersen11, Proposition 6.4.3, Theorem 6.5.7, and Section 8.12.8]), and
$A_\infty $
is a simple, unital AF-algebra which is antiliminary (see [Reference Pedersen11, Proposition 6.4.3, Theorem 6.5.7, and Section 8.12.8]), and
![]() $\mathcal {Z}$
is a simple, unital
$\mathcal {Z}$
is a simple, unital
![]() $\mathrm{C}^{*}$
-algebra which is nowhere scattered (see [Reference Thiel and Vilalta16, Remark 9.2]). But these
$\mathrm{C}^{*}$
-algebra which is nowhere scattered (see [Reference Thiel and Vilalta16, Remark 9.2]). But these
![]() $\mathrm{C}^{*}$
-algebras are stably finite (see [Reference Blackadar1, p. 420] and [Reference Rørdam14, p. 1]), and hence are not purely infinite. In particular,
$\mathrm{C}^{*}$
-algebras are stably finite (see [Reference Blackadar1, p. 420] and [Reference Rørdam14, p. 1]), and hence are not purely infinite. In particular,
![]() $A_\infty $
and
$A_\infty $
and
![]() $\mathcal {Z}$
do not have residual (HS
$\mathcal {Z}$
do not have residual (HS
![]() $_{\text {t}}$
), because if they had such a property, then since they are simple, they must be purely infinite (by [Reference Blanchard and Kirchberg2, Proposition 3.1]), a contradiction.
$_{\text {t}}$
), because if they had such a property, then since they are simple, they must be purely infinite (by [Reference Blanchard and Kirchberg2, Proposition 3.1]), a contradiction.
Proof of Corollary B
Note first that, by [Reference Blanchard and Kirchberg2, Remark 2.9(iv)] and [Reference Thiel and Vilalta15, Remark 3.2], any purely infinite
![]() $\mathrm{C}^{*}$
-algebra has the global (and so the weak) Glimm property. Thus the implication
$\mathrm{C}^{*}$
-algebra has the global (and so the weak) Glimm property. Thus the implication
![]() $(1) \Rightarrow (2)$
is true. The converse holds, by the proof of the implication
$(1) \Rightarrow (2)$
is true. The converse holds, by the proof of the implication
![]() $(5) \Rightarrow (6)$
of Theorem A (where the weak Glimm property is not necessary). Thus
$(5) \Rightarrow (6)$
of Theorem A (where the weak Glimm property is not necessary). Thus
![]() $(1)$
and
$(1)$
and
![]() $(2)$
are equivalent. Moreover, (locally) purely infinite
$(2)$
are equivalent. Moreover, (locally) purely infinite
![]() $\mathrm{C}^{*}$
-algebras have residual (HS
$\mathrm{C}^{*}$
-algebras have residual (HS
![]() $_t$
), by Remark 3.1, and residual (HI), by [Reference Kirchberg and Rørdam6, Theorem 4.16]. Thus the implications
$_t$
), by Remark 3.1, and residual (HI), by [Reference Kirchberg and Rørdam6, Theorem 4.16]. Thus the implications
![]() $(1) \Rightarrow (3)$
and
$(1) \Rightarrow (3)$
and
![]() $(1) \Rightarrow (4)$
hold. The converse implications hold by Theorem A.
$(1) \Rightarrow (4)$
hold. The converse implications hold by Theorem A.
Proof of Corollary C
Suppose that A is weakly purely infinite,
![]() $0\neq a\in A^+$
, and
$0\neq a\in A^+$
, and
![]() $\varepsilon>0$
. Then A is locally purely infinite (see [Reference Blanchard and Kirchberg2, Proposition 4.11]), and hence A has residual (HS
$\varepsilon>0$
. Then A is locally purely infinite (see [Reference Blanchard and Kirchberg2, Proposition 4.11]), and hence A has residual (HS
![]() $_0$
), by Remark 3.1. Thus
$_0$
), by Remark 3.1. Thus
![]() $\overline {aAa}$
has a nonzero, square-zero, element. But A has the weak Glimm property, and so there exists an element
$\overline {aAa}$
has a nonzero, square-zero, element. But A has the weak Glimm property, and so there exists an element
![]() $r \in \overline {aAa}$
with
$r \in \overline {aAa}$
with
![]() $r^2 = 0$
such that
$r^2 = 0$
such that
![]() $(a - \varepsilon )_+ \in \overline {ArA}$
. This shows that A has the global Glimm property. Now, by [Reference Kirchberg and Rørdam7, Proposition 4.15], A
$(a - \varepsilon )_+ \in \overline {ArA}$
. This shows that A has the global Glimm property. Now, by [Reference Kirchberg and Rørdam7, Proposition 4.15], A
Proof of Corollary D
To prove, use [Reference Enders and Shulman4, Corollary 5] and [Reference Thiel and Vilalta16, Theorem 3.1(
![]() $(1)\iff (2)$
)].
$(1)\iff (2)$
)].
Proof of Corollary E
It is known that a
![]() $\mathrm{C}^{*}$
-algebra with the global Glimm property is nowhere scattered [Reference Thiel and Vilalta15, Theorem 7.1], and so is strictly antiliminary (use [Reference Thiel and Vilalta16, Theorem 3.1(
$\mathrm{C}^{*}$
-algebra with the global Glimm property is nowhere scattered [Reference Thiel and Vilalta15, Theorem 7.1], and so is strictly antiliminary (use [Reference Thiel and Vilalta16, Theorem 3.1(
![]() $(1)\iff (2)$
)] – or Corollary D). This proves
$(1)\iff (2)$
)] – or Corollary D). This proves
![]() $ (1) \Rightarrow (2)$
and
$ (1) \Rightarrow (2)$
and
![]() $ (1) \Rightarrow (3)$
. For the converse implications, suppose that A has the weak Glimm property and is nowhere scattered (resp., antiliminary), and consider
$ (1) \Rightarrow (3)$
. For the converse implications, suppose that A has the weak Glimm property and is nowhere scattered (resp., antiliminary), and consider
![]() $a\in A^+$
and
$a\in A^+$
and
![]() $\varepsilon>0$
. By Corollary D, A has residual (HS
$\varepsilon>0$
. By Corollary D, A has residual (HS
![]() $_0$
) (resp., property (HS
$_0$
) (resp., property (HS
![]() $_0$
)). Thus
$_0$
)). Thus
![]() $\{0\} \neq S_0(\overline {aAa})$
, and hence, by the weak Glimm property, there is
$\{0\} \neq S_0(\overline {aAa})$
, and hence, by the weak Glimm property, there is
![]() $r \in \overline {aAa}$
such that
$r \in \overline {aAa}$
such that
![]() $r^2=0$
and
$r^2=0$
and
![]() $(a-\varepsilon )_+\in \overline {ArA}$
. This shows that A has the global Glimm property.
$(a-\varepsilon )_+\in \overline {ArA}$
. This shows that A has the global Glimm property.
Proof of Proposition F
![]() $(1) \Rightarrow (2)$
: Suppose that A has the global Glimm property and H is a hereditary
$(1) \Rightarrow (2)$
: Suppose that A has the global Glimm property and H is a hereditary
![]() $\mathrm{C}^{*}$
-subalgebra of A. Then H is a Noetherian
$\mathrm{C}^{*}$
-subalgebra of A. Then H is a Noetherian
![]() $\mathrm{C}^{*}$
-algebra with the global Glimm property (see [Reference Thiel and Vilalta15, Theorem 3.10]). Since H is Noetherian,
$\mathrm{C}^{*}$
-algebra with the global Glimm property (see [Reference Thiel and Vilalta15, Theorem 3.10]). Since H is Noetherian,
![]() $\mathrm {Prim}(H)$
is compact, and so H has a strictly full element h (see [Reference Pasnicu and Rouzbehani10, Lemma 2.1]). Thus, there exists
$\mathrm {Prim}(H)$
is compact, and so H has a strictly full element h (see [Reference Pasnicu and Rouzbehani10, Lemma 2.1]). Thus, there exists
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $(h-\varepsilon )_+$
is full in H. Since H has the global Glimm property, there is
$(h-\varepsilon )_+$
is full in H. Since H has the global Glimm property, there is
![]() $r \in S_0(\overline {hHh})$
such that
$r \in S_0(\overline {hHh})$
such that
![]() $(h-\varepsilon )_+\in \overline {HrH}$
. Hence
$(h-\varepsilon )_+\in \overline {HrH}$
. Hence
![]() $H=\overline {H(h-\varepsilon )_+H}\subseteq \overline {HrH},$
and so
$H=\overline {H(h-\varepsilon )_+H}\subseteq \overline {HrH},$
and so
![]() $H=\overline {HrH}$
. Thus,
$H=\overline {HrH}$
. Thus,
![]() $(1)$
implies
$(1)$
implies
![]() $(2)$
.
$(2)$
.
![]() $(2) \Rightarrow (1)$
: This is clear, since if
$(2) \Rightarrow (1)$
: This is clear, since if
![]() $a\in A^+$
,
$a\in A^+$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $A_a:=\overline {aAa}$
, then
$A_a:=\overline {aAa}$
, then
![]() $A_a$
has a square-zero element r with
$A_a$
has a square-zero element r with
![]() $A_a=\overline {A_arA_a}$
. Thus,
$A_a=\overline {A_arA_a}$
. Thus,
and so A has the global Glimm property.
Proof of Corollary G
By Corollary D, we only need to show
![]() $ (1) \Rightarrow (2)$
. Note that a Noetherian and Artinian
$ (1) \Rightarrow (2)$
. Note that a Noetherian and Artinian
![]() $\mathrm{C}^{*}$
-algebra A has a composition series of ideals as
$\mathrm{C}^{*}$
-algebra A has a composition series of ideals as
![]() $0 =I_0 \unlhd I_1\unlhd I_2 \unlhd \cdots \unlhd I_n=A$
such that
$0 =I_0 \unlhd I_1\unlhd I_2 \unlhd \cdots \unlhd I_n=A$
such that
![]() $I_j/I_{j-1}$
is simple for each
$I_j/I_{j-1}$
is simple for each
![]() $1\leq j \leq n$
. Since residual (HS
$1\leq j \leq n$
. Since residual (HS
![]() $_0$
) passes to ideals and quotients (see Remark 2.1), and the global Glimm property is preserved under extensions [Reference Thiel and Vilalta15, Theorem 3.10], it suffices to show that the implication holds for simple
$_0$
) passes to ideals and quotients (see Remark 2.1), and the global Glimm property is preserved under extensions [Reference Thiel and Vilalta15, Theorem 3.10], it suffices to show that the implication holds for simple
![]() $\mathrm{C}^{*}$
-algebras. But this is obvious, since if A is simple with residual (HS
$\mathrm{C}^{*}$
-algebras. But this is obvious, since if A is simple with residual (HS
![]() $_0$
),
$_0$
),
![]() $a\in A^+$
, and
$a\in A^+$
, and
![]() $\varepsilon>0$
, then there is
$\varepsilon>0$
, then there is
![]() $r \in S_0(\overline {aAa})$
such that
$r \in S_0(\overline {aAa})$
such that
![]() $(a-\varepsilon )_+\in \overline {ArA}=A$
.
$(a-\varepsilon )_+\in \overline {ArA}=A$
.
The results obtained above give partial positive answers to questions (1)–(3) of Section 1. We recall that question (1) asks whether the four properties s.p.i., p.i., w.p.i., and l.p.i. are always equivalent. Corollary C shows that having the assumption “the weak Glimm property” implies that the two properties p.i. and w.p.i. are equivalent, and Theorem A(
![]() $(1)\Leftrightarrow (6)\Leftrightarrow (7)$
) shows that if we also have the assumption “the absolute value of every nonzero, square-zero, element is properly infinite,” then the three properties p.i., w.p.i., and l.p.i. are equivalent. Also, question (2) asks if the two properties being nowhere scattered and the global Glimm property are always equivalent. Corollaries E and G show that these two properties are equivalent for all
$(1)\Leftrightarrow (6)\Leftrightarrow (7)$
) shows that if we also have the assumption “the absolute value of every nonzero, square-zero, element is properly infinite,” then the three properties p.i., w.p.i., and l.p.i. are equivalent. Also, question (2) asks if the two properties being nowhere scattered and the global Glimm property are always equivalent. Corollaries E and G show that these two properties are equivalent for all
![]() $\mathrm{C}^{*}$
-algebras with the weak Glimm property and all Artinian and Noetherian
$\mathrm{C}^{*}$
-algebras with the weak Glimm property and all Artinian and Noetherian
![]() $\mathrm{C}^{*}$
-algebras. Finally, question (3) asks whether the two properties p.i. and residual (HI) are always equivalent. Theorem A(
$\mathrm{C}^{*}$
-algebras. Finally, question (3) asks whether the two properties p.i. and residual (HI) are always equivalent. Theorem A(
![]() $ (6) \Leftrightarrow (8)$
) shows that with the two assumptions “the weak Glimm property” and “the absolute value of every nonzero, square-zero, element is properly infinite,” the two properties p.i. and residual (HI) are equivalent.
$ (6) \Leftrightarrow (8)$
) shows that with the two assumptions “the weak Glimm property” and “the absolute value of every nonzero, square-zero, element is properly infinite,” the two properties p.i. and residual (HI) are equivalent.