Hostname: page-component-5cf477f64f-zrtmk Total loading time: 0 Render date: 2025-03-28T01:31:14.529Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLICATIVE (IN)STABILITY OF BANACH ALGEBRAS

Part of: Model theory Abstract harmonic analysis Topological algebras, normed rings and algebras, Banach algebras Selfadjoint operator algebras

Published online by Cambridge University Press:  17 March 2025

STEFANO FERRI Open the ORCID record for STEFANO FERRI [Opens in a new window]  and
MATTHIAS NEUFANG Open the ORCID record for MATTHIAS NEUFANG [Opens in a new window]
STEFANO FERRI*
Affiliation:
Departamento de Matemáticas, Universidad de los Andes, Carrera 1 N. 18A–10, Bogotá D.C., Apartado Aéreo 4976, Colombia
MATTHIAS NEUFANG
Affiliation:
School of Mathematics and Statistics, Carleton University, 1125 Colonel By Drive, Ottawa, Ontario K1S 5B6, Canada and Laboratoire de Mathématiques Paul Painlevé (UMR CNRS 8524), Université Lille 1 – Sciences et Technologies, UFR de Mathématiques, 59655 Villeneuve d’Ascq Cedex, France e-mail: [email protected], [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The concept of stability has proved very useful in the field of Banach space geometry. In this note, we introduce and study a corresponding concept in the setting of Banach algebras, which we call multiplicative stability. As we shall prove, various interesting examples of Banach algebras are multiplicatively unstable, and hence unstable in the model-theoretic sense. The examples include Fourier algebras over noncompact amenable groups, 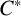$C^*$-algebras and the measure algebra of an infinite compact group.

Keywords

model theoretic stabilityBanach space stabilitymultiplicative stabilityBanach algebra stability

MSC classification

Primary: 46H20: Structure, classification of topological algebras
Secondary: 03C98: Applications of model theory 43A10: Measure algebras on groups, semigroups, etc. 43A60: Almost periodic functions on groups and semigroups and their generalizations (recurrent functions, distal functions, etc.); almost automorphic functions 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the Faculty of Sciences of Universidad de los Andes via the grant ‘Banach algebras, Arens products and applications’ of ‘Programa de investigación profesores de planta’ (Convocatoria 2018–2019). The second author was partially supported by NSERC (RGPIN-2014-06356). This support is gratefully acknowledged.

References

Alabkary, N., A dynamical hierarchy of Banach algebras, PhD Thesis, Carleton University, 2022.Google Scholar
Alabkary, N., ‘Hyper-instability of Banach algebras’, AIMS Math. 9(6) (2024), 14012–14025.CrossRefGoogle Scholar
Berglund, J. F., Junghenn, H. D. and Milnes, P., Analysis on Semigroups. Function Spaces, Compactifications, Representations, Canadian Mathematical Society Series of Monographs and Advanced Texts, 13 (John Wiley, New York, 1989).Google Scholar
Blackadar, B., Operator Algebras. Theory of ${C}^{\ast }$ -algebras and von Neumann Algebras, Encyclopaedia of Mathematical Sciences, 122, Operator Algebras and Non-commutative Geometry III (Springer-Verlag, Berlin, 2006).Google Scholar
Dales, H. G. and Lau, A. T.-M., ‘The second duals of Beurling algebras’, Mem. Amer. Math. Soc. 177(836) (2005), 191 pages.Google Scholar
Dales, H. G., Lau, A. T.-M. and Strauss, D., ‘Second duals of measure algebras’, Dissertationes Math. 481 (2012), 1–121.CrossRefGoogle Scholar
Farah, I., Hart, B. and Sherman, D., ‘Model theory of operator algebras I: stability’, Bull. Lond. Math. Soc. 45(4) (2013), 825–838.CrossRefGoogle Scholar
Farah, I., Hart, B. and Sherman, D., ‘Model theory of operator algebras II: model theory’, Israel J. Math. 201(1) (2014), 477–505.CrossRefGoogle Scholar
Glasner, E. and Megrelishvili, M., ‘More on tame dynamical systems’, in: Ergodic Theory and Dynamical Systems in their Interactions with Arithmetics and Combinatorics, Lecture Notes in Mathematics, 2213 (eds. Ferenczi, S., Kulaga-Przymus, J. and Lemańczyk, M.) (Springer, Cham, 2018), 351–392.CrossRefGoogle Scholar
Guerre, S. and Lapresté, J.-T., ‘Quelques propriétés des espaces de Banach stables’, Israel J. Math. 39(3) (1981), 247–254.CrossRefGoogle Scholar
Hennefeld, J., ‘A note on the Arens products’, Pacific J. Math. 26 (1968), 115–119.CrossRefGoogle Scholar
Herz, C., ‘Harmonic synthesis for subgroups’, Ann. Inst. Fourier (Grenoble) 23(3) (1973), 91–123.CrossRefGoogle Scholar
Iovino, J., ‘Stable Banach spaces and Banach space structures. I. Fundamentals’, in: Models, Algebras, and Proofs (Bogotá, 1995), Lecture Notes in Pure and Applied Mathematics, 203, (eds. Caicedo, X. and Montenegro, C. H.) (Dekker, New York, 1999), 77–95.Google Scholar
Iovino, J., Applications of Model Theory to Functional Analysis (Dover Publications, Inc., Mineola, New York, 2014).Google Scholar
Kalton, N. J., ‘The nonlinear geometry of Banach spaces’, Rev. Mat. Complut. 21(1) (2008), 7–60.CrossRefGoogle Scholar
Kaniuth, E., A Course in Commutative Banach Algebras, Graduate Texts in Mathematics, 246 (Springer-Verlag, New York, 2009).CrossRefGoogle Scholar
Kaniuth, E. and Lau, A. T.-M., Fourier and Fourier–Stieltjes Algebras on Locally Compact Groups, Mathematical Surveys and Monographs, 231 (American Mathematical Society, Providence, RI, 2018).CrossRefGoogle Scholar
Krivine, J.-L. and Maurey, B., ‘Espaces de Banach stables’, Israel J. Math. 39(4) (1981), 273–295.CrossRefGoogle Scholar
Ogasawara, T., ‘Finite-dimensionality of certain Banach algebras’, J. Sci. Hiroshima Univ. Ser. A. 17 (1954), 359–364.Google Scholar
Pym, J. S., ‘The convolution of functionals on spaces of bounded functions’, Proc. Lond. Math. Soc. (3) 15 (1965), 84–104.Google Scholar
Raynaud, Y., ‘Espaces de Banach superstables, distances stables et homéomorphismes uniformes’, Israel J. Math. 44(1) (1983), 33–52.CrossRefGoogle Scholar
Sakai, S., ‘Weakly compact operators on operator algebras’, Pacific J. Math. 14 (1964), 659–664.CrossRefGoogle Scholar
Zelmanov, E. I., ‘On periodic compact groups’, Israel J. Math. 77(1–2) (1992), 83–95.CrossRefGoogle Scholar