No CrossRef data available.
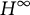 $H^{\infty }$ symbols
$H^{\infty }$ symbolsPublished online by Cambridge University Press: 10 December 2024
In the present paper, we characterize the Fredholmness of Toeplitz pairs on Hardy space over the bidisk with the bounded holomorphic symbols, and hence, we obtain the index formula for such Toeplitz pairs. The key to obtain the Fredholmness of such Toeplitz pairs is the  $L^p$ solution of Corona Problem over
$L^p$ solution of Corona Problem over 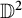 $\mathbb {D}^2$.
$\mathbb {D}^2$.
This work is supported by NSFC: (12271298 and 11871308).