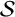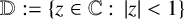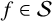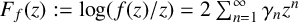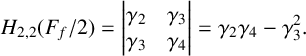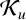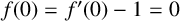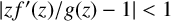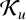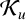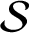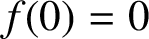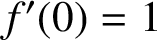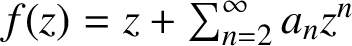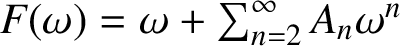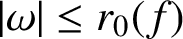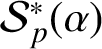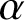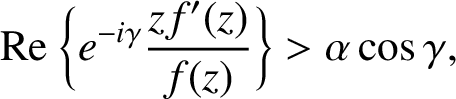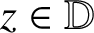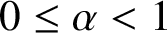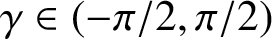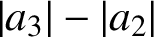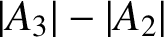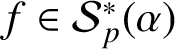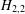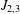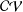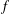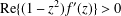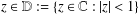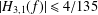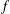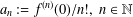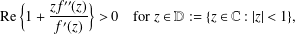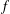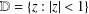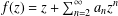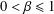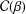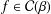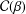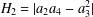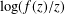15 results
THE SHARP BOUND OF THE SECOND HANKEL DETERMINANT OF LOGARITHMIC COEFFICIENTS FOR STARLIKE AND CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
The Schwarzian norm estimates for Janowski convex functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 299-315
-
- Article
-
- You have access
- HTML
- Export citation
ON CERTAIN CLOSE-TO-CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 365-375
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Peaking and interpolation by complex polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 129-138
-
- Article
- Export citation
A NOTE ON SPIRALLIKE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 25 March 2021, pp. 117-123
- Print publication:
- February 2022
-
- Article
- Export citation
INTEGRAL MEANS OF UNIVALENT FUNCTIONS ON AN ANNULUS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 September 2020, p. 512
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
11 - The ⋆-Function in Complex Analysis
-
- Book:
- Symmetrization in Analysis
- Published online:
- 22 February 2019
- Print publication:
- 14 March 2019, pp 398-453
-
- Chapter
- Export citation
SHARP BOUNDS OF SOME COEFFICIENT FUNCTIONALS OVER THE CLASS OF FUNCTIONS CONVEX IN THE DIRECTION OF THE IMAGINARY AXIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 86-96
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
THE SHARP BOUND FOR THE HANKEL DETERMINANT OF THE THIRD KIND FOR CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 435-445
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Applications of differential subordinations for norm estimates of an integral operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 06 November 2017, pp. 281-291
- Print publication:
- April 2018
-
- Article
- Export citation
INVARIANCE OF THE COEFFICIENTS OF STRONGLY CONVEX FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 23 November 2016, pp. 436-445
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Pontryagin’s Maximum Principle for the Loewner Equation in Higher Dimensions
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 4 / 01 August 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 942-960
- Print publication:
- 01 August 2015
-
- Article
-
- You have access
- Export citation
RADIAL AND TANGENTIAL GROWTH OF CLOSE-TO-CONVEX FUNCTIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 48 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 15 February 2005, pp. 231-240
-
- Article
-
- You have access
- Export citation
Smale's mean value conjecture for odd polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 409-412
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Certain generalizations of presetarlike functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 3 / November 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 325-334
- Print publication:
- November 1979
-
- Article
-
- You have access
- Export citation