Published online by Cambridge University Press: 12 February 2024
For  $-1\leq B \lt A\leq 1$, let
$-1\leq B \lt A\leq 1$, let 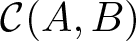 $\mathcal{C}(A,B)$ denote the class of normalized Janowski convex functions defined in the unit disk
$\mathcal{C}(A,B)$ denote the class of normalized Janowski convex functions defined in the unit disk  $\mathbb{D}:=\{z\in\mathbb{C}:|z| \lt 1\}$ that satisfy the subordination relation
$\mathbb{D}:=\{z\in\mathbb{C}:|z| \lt 1\}$ that satisfy the subordination relation  $1+zf''(z)/f'(z)\prec (1+Az)/(1+Bz)$. In the present article, we determine the sharp estimate of the Schwarzian norm for functions in the class
$1+zf''(z)/f'(z)\prec (1+Az)/(1+Bz)$. In the present article, we determine the sharp estimate of the Schwarzian norm for functions in the class  $\mathcal{C}(A,B)$. The Dieudonné’s lemma which gives the exact region of variability for derivatives at a point of bounded functions, plays the key role in this study, and we also use this lemma to construct the extremal functions for the sharpness by a new method.
$\mathcal{C}(A,B)$. The Dieudonné’s lemma which gives the exact region of variability for derivatives at a point of bounded functions, plays the key role in this study, and we also use this lemma to construct the extremal functions for the sharpness by a new method.