Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-05-02T08:28:36.129Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CERTAIN CLOSE-TO-CONVEX FUNCTIONS

Part of: Geometric function theory

Published online by Cambridge University Press:  17 July 2023

MD FIROZ ALI Open the ORCID record for MD FIROZ ALI [Opens in a new window]  and
MD NUREZZAMAN Open the ORCID record for MD NUREZZAMAN [Opens in a new window]
MD FIROZ ALI*
Affiliation:
National Institute of Technology Durgapur, Mahatma Gandhi Road, Durgapur, Durgapur-713203, West Bengal, India e-mail: [email protected]
MD NUREZZAMAN
Affiliation:
National Institute of Technology Durgapur, Mahatma Gandhi Road, Durgapur, Durgapur-713203, West Bengal, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 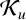$\mathcal {K}_u$ denote the class of all analytic functions f in the unit disk 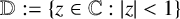$\mathbb {D}:=\{z\in \mathbb {C}:|z|<1\}$, normalised by 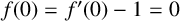$f(0)=f'(0)-1=0$ and satisfying 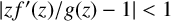$|zf'(z)/g(z)-1|<1$ in $\mathbb {D}$ for some starlike function g. Allu, Sokól and Thomas [‘On a close-to-convex analogue of certain starlike functions’, Bull. Aust. Math. Soc. 108 (2020), 268–281] obtained a partial solution for the Fekete–Szegö problem and initial coefficient estimates for functions in 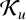$\mathcal {K}_u$, and posed a conjecture in this regard. We prove this conjecture regarding the sharp estimates of coefficients and solve the Fekete–Szegö problem completely for functions in the class 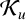$\mathcal {K}_u$.

Keywords

analytic functionsunivalent functionsstarlike functionsconvex functionsclose-to-convex function

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Secondary: 30C55: General theory of univalent and multivalent functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 2 , April 2024 , pp. 365 - 375
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Allu, V., Sokól, J. and Thomas, D. K., ‘On a close-to-convex analogue of certain starlike functions’, Bull. Aust. Math. Soc. 108 (2020), 268–281.CrossRefGoogle Scholar
Becker, J., ‘Löwnersche Differentialgleichung und quasikonform fortsetzbare schlichte Funktionen’, J. reine angew. Math 255 (1972), 23–43.Google Scholar
Becker, J. and Pommerenke, C., ‘Schlichtheitskriterien und Jordangebiete’, J. reine angew. Math. 354 (1984), 74–94.Google Scholar
Choi, N. E., Kim, Y. C. and Sugawa, T., ‘A general approach to the Fekete–Szegö problem’, J. Math. Soc. Japan 59 (2007), 707–727.CrossRefGoogle Scholar
Duren, P. L., Univalent Functions, Grundlehren der mathematischen Wissenschaften, 259 (Springer-Verlag, New York–Berlin–Heidelberg–Tokyo, 1983).Google Scholar
Fekete, M. and Szegö, G., ‘Eine Bemerkung über ungerade schlichte Funktionen’, J. Lond. Math. Soc. 8 (1933), 85–89.CrossRefGoogle Scholar
Goodman, A. W., Univalent Functions, Vol. I and II (Mariner Publishing Co., Tampa, FL, 1983).Google Scholar
Hallenbeck, D. J. and Macgregor, T. H., Linear Problems and Convexity Techniques in Geometric Function Theory, Monographs and Studies in Mathematics, 22 (Pitman, Boston, MA, 1984).Google Scholar
Kanas, S. and Lecko, A., ‘On the Fekete–Szegö problem and the domain of convexity for a certain class of univalent functions’, Folia Sci. Univ. Tech. Resoviensis 73 (1990), 49–57.Google Scholar
Kaplan, W., ‘Close-to-convex schlicht functions’, Michigan Math. J. 1 (1952), 169–185.CrossRefGoogle Scholar
Kim, Y. C. and Sugawa, T., ‘Growth and coefficient estimates for uniformly locally univalent functions on the unit disk’, Rocky Mountain J. Math. 32 (2002), 179–200.CrossRefGoogle Scholar
Koepf, W., ‘On the Fekete–Szegö problem for close-to-convex functions’, Proc. Amer. Math. Soc. 101 (1987), 89–95.Google Scholar
Koepf, W., ‘On the Fekete–Szegö problem for close-to-convex functions II’, Arch. Math. 49 (1987), 420–433.CrossRefGoogle Scholar
Kowalczyk, B. and Lecko, A., ‘Fekete–Szegö problem for a certain subclass of close-to-convex functions’, Bull. Malays. Math. Sci. Soc. 38(2) (2015), 1393–1410.CrossRefGoogle Scholar
London, R. R., ‘Fekete–Szegö inequalities for close-to-convex functions’, Proc. Amer. Math. Soc. 117 (1993), 947–950.Google Scholar
Singh, R., ‘On a class of starlike functions’, Compos. Math. 19 (1968), 78–82.Google Scholar
Singh, R. and Singh, V., ‘On a class of bounded starlike functions’, Indian J. Pure Appl. Math. 5(8) (1974), 733–754.Google Scholar
Yamashita, S., ‘Almost locally univalent functions’, Monatsh. Math. 81 (1976), 235–240.CrossRefGoogle Scholar
Yamashita, S., ‘Norm estimates for function starlike or convex of order alpha’, Hokkaido Math. J. 28(1) (1999), 217–230 (summary in English).CrossRefGoogle Scholar