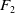8 results
Continuously many quasi-isometry classes of residually finite groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 569-572
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric actions and finite approximations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2464-2470
- Print publication:
- July 2023
-
- Article
- Export citation
Residually finite tubular groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 27 August 2019, pp. 2937-2951
- Print publication:
- December 2020
-
- Article
- Export citation
ON RESIDUALLY FINITE VARIETIES OF INVOLUTION SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 December 2010, pp. 181-198
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
OUTER AUTOMORPHISM GROUPS OF CERTAIN TREE PRODUCTS OF ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
A finite basis theorem for residually finite, congruence meet-semidistributive varieties
-
- Journal:
- The Journal of Symbolic Logic / Volume 65 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 12 March 2014, pp. 187-200
- Print publication:
- March 2000
-
- Article
- Export citation
Cyclic Subgroup Separability of HNN-Extensions with Cyclic Associated Subgroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 3 / 01 September 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 335-343
- Print publication:
- 01 September 1999
-
- Article
-
- You have access
- Export citation
Cyclic Subgroup Separability of Generalized Free Products
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 3 / 01 September 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 296-302
- Print publication:
- 01 September 1993
-
- Article
-
- You have access
- Export citation