Research Article
CHARACTERIZATIONS OF HYPERSURFACES OF TYPE A2 IN A COMPLEX PROJECTIVE SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 1-8
-
- Article
-
- You have access
- Export citation
OUTER AUTOMORPHISM GROUPS OF CERTAIN TREE PRODUCTS OF ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
-
- Article
-
- You have access
- Export citation
A MODEL OF UNIVERSAL TEICHMÜLLER SPACE AND ITS APPLICATION
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 21-30
-
- Article
-
- You have access
- Export citation
COMMUTATIVITY DEGREES OF WREATH PRODUCTS OF FINITE ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 31-36
-
- Article
-
- You have access
- Export citation
ON THE FUNDAMENTAL REGIONS OF A FIXED POINT FREE CONSERVATIVE HÉNON MAP
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 37-48
-
- Article
-
- You have access
- Export citation
SCHUR MULTIPLICATIVE MAPS ON MATRICES
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 49-72
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE STIELTJES INTEGRAL FOR (φ,Φ)-LIPSCHITZIAN INTEGRATORS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-90
-
- Article
-
- You have access
- Export citation
A NOTE ON A RESULT OF RUZSA
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 91-98
-
- Article
-
- You have access
- Export citation
PINCHING THEOREMS FOR A COMPACT MINIMAL SUBMANIFOLD IN A COMPLEX PROJECTIVE SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 99-114
-
- Article
-
- You have access
- Export citation
ON THE METHOD OF APPROXIMATION FOR EVOLUTIONARY INCLUSIONS OF PSEUDOMONOTONE TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 115-143
-
- Article
-
- You have access
- Export citation
A PROPERTY OF CLOSED FINITE TYPE CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 145-149
-
- Article
-
- You have access
- Export citation
INDECOMPOSABILITY GRAPHS OF RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 151-159
-
- Article
-
- You have access
- Export citation
COMPACT DIFFERENCES OF COMPOSITION OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 161-165
-
- Article
-
- You have access
- Export citation
ON THE STABILITY OF A MIXED-TYPE LINEAR AND QUADRATIC FUNCTIONAL EQUATION
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 167-176
-
- Article
-
- You have access
- Export citation


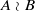 of finite Abelian groups
of finite Abelian groups 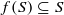 for different subsets
for different subsets 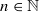 and
and 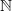 . Erdös and Turán conjectured that, for any basis
. Erdös and Turán conjectured that, for any basis 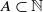 for which
for which 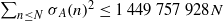 for large enough
for large enough 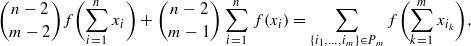
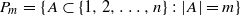 , and 1<
, and 1<