Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T05:03:50.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclic Subgroup Separability of HNN-Extensions with Cyclic Associated Subgroups

Published online by Cambridge University Press:  20 November 2018

Goansu Kim  and
C. Y. Tang
Goansu Kim
Affiliation:
Department of Mathematics Yeungnam University Kyongsan, 712-749 Korea, email: [email protected]
C. Y. Tang
Affiliation:
University of Waterloo Waterloo, Ontario N2L 3G1, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

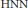We derive a necessary and sufficient condition for $\text{HNN}$-extensions of cyclic subgroup separable groups with cyclic associated subgroups to be cyclic subgroup separable. Applying this, we explicitly characterize the residual finiteness and the cyclic subgroup separability of 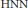$\text{HNN}$-extensions of abelian groups with cyclic associated subgroups. We also consider these residual properties of 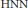$\text{HNN}$-extensions of nilpotent groups with cyclic associated subgroups.

Keywords

20E2620E0620F10HNN-extensionnilpotent groupscyclic subgroup separable (πcresidually finite
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 3 , 01 September 1999 , pp. 335 - 343
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Allenby, R. B. J. T. and Tang, C. Y., The residual finiteness of some one-relator groups with torsion. J. Algebra (1) 71 (1981), 132–140.Google Scholar
[2] Allenby, R. B. J. T. and Tang, C. Y., Conjugacy separability of certain 1-relator groups with torsion. J. Algebra (1) 103 (1986), 619–637.Google Scholar
[3] Andreadakis, S., Raptis, E., and Varsos, D., A characterization of residually finite HNN-extensions of finitely generated abelian groups. Arch. Math. 50 (1988), 495–501.Google Scholar
[4] Kim, G., Cyclic subgroup separability of HNN extensions. Bull. KoreanMath. Soc. (2) 30 (1993), 285–293.Google Scholar
[5] Kimand, G., Tang, C. Y., Conjugacy separability of HNN-extensions of abelian groups. Arch. Math. 67 (1996), 353–359.Google Scholar
[6] Kimand, G., Tang, C. Y., A criterion for the conjugacy separability of amalgamated free products of conjugacy separable groups. J. Algebra 184 (1996), 1052–1072.Google Scholar
[7] Meskin, S., Non residually finite one-relator groups. Trans. Amer.Math. Soc. 164 (1972), 105–114.Google Scholar
[8] Niblo, G. A., HNN extensions of a free group by Z which are subgroup separable. Proc. London Math. Soc. 61 (1990), 18–32.Google Scholar
[9] Robinson, D. J. S., A course in the theory of groups. Graduate Texts in Math. 80, Springer-Verlag, New York-Heidelberg-Berlin, 1982.Google Scholar
[10] Rosenberger, G. and Sasse, S. L., Residual properties of HNN-extensions with cyclic associated subgroups. Algebra Colloq. (1) 3 (1996), 91–96.Google Scholar
[11] Stebe, P. F., Residual finiteness of a class of knot groups. Comm. Pure. Appl. Math. 21 (1968), 563–583.Google Scholar
[12] Tang, C. Y., Conjugacy separability of generalized free products of certain conjugacy separable groups. Canad. Math. Bull. (1) 38 (1995), 120–127.Google Scholar
[13] Tang, C. Y., Conjugacy separability of generalized free products of surface groups. J. Pure Appl. Algebra 120 (1997), 187–194.Google Scholar
[14] Thurston, W. F., Three dimensional manifolds, Kleinian groups and hyperbolic geometry. Bull. Amer. Math. Soc. 6 (1982), 357–381.Google Scholar