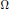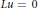6 results
Chapter 6 - Scalar curvature deformation and the Einstein constraint equations
-
- Book:
- Lectures on Mathematical Relativity
- Published online:
- 03 April 2025
- Print publication:
- 10 April 2025, pp 167-230
-
- Chapter
- Export citation
Unconditional convergence of eigenfunction expansions for abstract and elliptic operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 April 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homogenization and norm-resolvent convergence for elliptic operators in a strip perforated along a curve
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1115-1158
- Print publication:
- December 2016
-
- Article
- Export citation
Matched Asymptotic Expansions of the Eigenvalues of a 3-D Boundary-Value Problem Relative to Two Cavities Linked by a Hole of Small Size
-
- Journal:
- Communications in Computational Physics / Volume 11 / Issue 2 / February 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 456-471
- Print publication:
- February 2012
-
- Article
- Export citation
REILLY INEQUALITIES OF ELLIPTIC OPERATORS ON CLOSED SUBMANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 335-346
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Approximation on Closed Sets by Analytic or Meromorphic Solutions of Elliptic Equations and Applications
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 5 / 01 October 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 945-969
- Print publication:
- 01 October 2002
-
- Article
-
- You have access
- Export citation