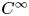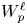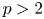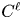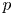1. Introduction
Let $(X,\,\|\cdot \|)$![]() be a complex or real Banach space. A series $\sum _{n=1}^{\infty }x_{n}$
be a complex or real Banach space. A series $\sum _{n=1}^{\infty }x_{n}$![]() formed by elements $x_{n}\in X$
formed by elements $x_{n}\in X$![]() is called unconditionally convergent in $X$
is called unconditionally convergent in $X$![]() if the rearranged series $\sum _{n=1}^{\infty }x_{\sigma (n)}$
if the rearranged series $\sum _{n=1}^{\infty }x_{\sigma (n)}$![]() converges in $X$
converges in $X$![]() for an arbitrary permutation $\sigma :\mathbb {N}\leftrightarrow \mathbb {N}$
for an arbitrary permutation $\sigma :\mathbb {N}\leftrightarrow \mathbb {N}$![]() . In this case there exists a unique element $x\in X$
. In this case there exists a unique element $x\in X$![]() such that $\sum _{n=1}^{\infty }x_{\sigma (n)}=x$
such that $\sum _{n=1}^{\infty }x_{\sigma (n)}=x$![]() for every permutation $\sigma$
for every permutation $\sigma$![]() . If $\sum _{n=1}^{\infty }\|x_{n}\|<\infty$
. If $\sum _{n=1}^{\infty }\|x_{n}\|<\infty$![]() , then the original series is called absolutely convergent in $X$
, then the original series is called absolutely convergent in $X$![]() . Every absolutely convergent series in $X$
. Every absolutely convergent series in $X$![]() converges unconditionally therein. If the space is finite-dimensional, then the converse is true according to Riemann's theorem. However, if $X$
converges unconditionally therein. If the space is finite-dimensional, then the converse is true according to Riemann's theorem. However, if $X$![]() is infinite-dimensional, then there exist unconditionally convergent series in $X$
is infinite-dimensional, then there exist unconditionally convergent series in $X$![]() that do not converge absolutely (as the Dvoretzky–Rogers theorem states [Reference Dvoretzky and Rogers13]).
that do not converge absolutely (as the Dvoretzky–Rogers theorem states [Reference Dvoretzky and Rogers13]).
In this paper, we study series in abstract and function spaces with two norms. The weaker norm among the two is induced by an inner product. Terms of series are pairwise orthogonal and are eigenfunctions of a certain (generally, unbounded) normal operator. Specifically, it may be a self-adjoint operator with discrete spectrum.
The simplest example of such type is given by the trigonometric Fourier series. From the operator-theoretic viewpoint, this is the spectral expansion of a function corresponding to the Laplace operator on the unit circle $\mathbb {T}$![]() . The study of the convergence of such series has a very long history and huge literature (see e.g. monographs [Reference Bary (Bari)8, Reference Edwards14, Reference Zygmund36], surveys [Reference Alimov, Il'in and Nikishin2, Reference Alimov, Il'in and Nikishin3, Reference Golubov16] and references therein).
. The study of the convergence of such series has a very long history and huge literature (see e.g. monographs [Reference Bary (Bari)8, Reference Edwards14, Reference Zygmund36], surveys [Reference Alimov, Il'in and Nikishin2, Reference Alimov, Il'in and Nikishin3, Reference Golubov16] and references therein).
It is known that the trigonometric Fourier series of every function $f(\tau )$![]() from the Lebesgue space $L_{p}(\mathbb {T})$
from the Lebesgue space $L_{p}(\mathbb {T})$![]() , with $1< p<\infty$
, with $1< p<\infty$![]() , converges to $f$
, converges to $f$![]() in this space. This is true for the Fourier series with respect to any rearranged trigonometric system
in this space. This is true for the Fourier series with respect to any rearranged trigonometric system

if and only if $p=2$![]() . Moreover, there exists a certain permutation $\sigma$
. Moreover, there exists a certain permutation $\sigma$![]() and a continuous function $f$
and a continuous function $f$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() such that series (1.1) does not converge to $f$
such that series (1.1) does not converge to $f$![]() in the space $L_{p}(\mathbb {T})$
in the space $L_{p}(\mathbb {T})$![]() whatever $p>2$
whatever $p>2$![]() [Reference Ul'janov (Ul'yanov)35, Theorem 8]. Let us indicate another example. The Carleson theorem [Reference Carleson12] states that the Fourier trigonometric series of any function $f\in L_{2}(\mathbb {T})$
[Reference Ul'janov (Ul'yanov)35, Theorem 8]. Let us indicate another example. The Carleson theorem [Reference Carleson12] states that the Fourier trigonometric series of any function $f\in L_{2}(\mathbb {T})$![]() converges to $f$
converges to $f$![]() almost everywhere (a.e.) on $\mathbb {T}$
almost everywhere (a.e.) on $\mathbb {T}$![]() . However, as was shown by Kolmogorov [Reference Kolmogoroff (Kolmogorov) and Menchoff (Men'shov)21], there exists a function $f\in L_{2}(\mathbb {T})$
. However, as was shown by Kolmogorov [Reference Kolmogoroff (Kolmogorov) and Menchoff (Men'shov)21], there exists a function $f\in L_{2}(\mathbb {T})$![]() such that its certain rearranged Fourier series of form (1.1) diverges a.e. on $\mathbb {T}$
such that its certain rearranged Fourier series of form (1.1) diverges a.e. on $\mathbb {T}$![]() . Thus, conditions for function series to be convergent or unconditionally convergent can be essentially different.
. Thus, conditions for function series to be convergent or unconditionally convergent can be essentially different.
The study of solutions to initial-boundary-value problems for parabolic or hyperbolic differential equations in cylindrical domains by the Fourier method leads to the analysis of the convergence of expansions in eigenfunctions of self-adjoint elliptic differential operators in bounded Euclidean domains (see e.g. [Reference Il'in19, Reference Ladyženskaya (Ladyzhenskaya)24, Reference Maurin30]). Let $G$![]() be a bounded domain in $\mathbb {R}^{n}$
be a bounded domain in $\mathbb {R}^{n}$![]() with smooth boundary, and suppose that an elliptic differential expression with smooth coefficients on $\overline {G}$
with smooth boundary, and suppose that an elliptic differential expression with smooth coefficients on $\overline {G}$![]() induces a self-adjoint operator $L$
induces a self-adjoint operator $L$![]() with discrete spectrum in the Hilbert space $L_{2}(G)$
with discrete spectrum in the Hilbert space $L_{2}(G)$![]() . Then this space possesses an orthonormal basis $\{e_{j}(\tau ):j\in \mathbb {N}\}$
. Then this space possesses an orthonormal basis $\{e_{j}(\tau ):j\in \mathbb {N}\}$![]() formed by eigenfunctions of $L$
formed by eigenfunctions of $L$![]() . Choosing a function $f\in L_{2}(G)$
. Choosing a function $f\in L_{2}(G)$![]() arbitrarily, we consider its spectral expansion
arbitrarily, we consider its spectral expansion
Here, $\lambda _{j}$![]() is the eigenvalue of $L$
is the eigenvalue of $L$![]() associated with the eigenfunction $e_{j}$
associated with the eigenfunction $e_{j}$![]() , and $c_{j}(f)$
, and $c_{j}(f)$![]() is the Fourier coefficient of $f$
is the Fourier coefficient of $f$![]() with respect to $e_{j}$
with respect to $e_{j}$![]() . This expansion converges in the $L_{2}(G)$
. This expansion converges in the $L_{2}(G)$![]() norm. Therefore, it is reasonable to ask under which supplementary conditions for $f$
norm. Therefore, it is reasonable to ask under which supplementary conditions for $f$![]() expansion (1.2) converges to $f$
expansion (1.2) converges to $f$![]() in the stronger $L_{p}(G)$
in the stronger $L_{p}(G)$![]() norm with $p>2$
norm with $p>2$![]() or uniformly on $G$
or uniformly on $G$![]() . There are no comprehensive answers to this question yet even in the case of ordinary differential equations. Results obtained in the many-dimensional case show that it is necessary to narrow down the problem statement essentially and to consider the convergence of the Fourier series (1.2) not for single functions but on the classes of differential functions with compact supports in the domain $G$
. There are no comprehensive answers to this question yet even in the case of ordinary differential equations. Results obtained in the many-dimensional case show that it is necessary to narrow down the problem statement essentially and to consider the convergence of the Fourier series (1.2) not for single functions but on the classes of differential functions with compact supports in the domain $G$![]() . Let us formulate one complete result of this type, which became a starting point for us [Reference Alimov, Il'in and Nikishin2, Chapter II, § 3, Subsection 2].
. Let us formulate one complete result of this type, which became a starting point for us [Reference Alimov, Il'in and Nikishin2, Chapter II, § 3, Subsection 2].
Let $W^{s}_{p,0}(G)$![]() denote the class of all functions that belong to the $L_{p}$
denote the class of all functions that belong to the $L_{p}$![]() -Sobolev space of real order $s>0$
-Sobolev space of real order $s>0$![]() over $G$
over $G$![]() and that their supports are compact subsets of the open set $G$
and that their supports are compact subsets of the open set $G$![]() . Spectral expansion (1.2) of an arbitrary function $f\in W^{s}_{p,0}(G)$
. Spectral expansion (1.2) of an arbitrary function $f\in W^{s}_{p,0}(G)$![]() converges uniformly on every compact set $K\subset G$
converges uniformly on every compact set $K\subset G$![]() if and only if the following three conditions are satisfied:
if and only if the following three conditions are satisfied:
Note that the first inequality guarantees the continuity functions of class $W^{s}_{p,0}(G)$![]() , whereas the second inequality provides the validity of the localization principle for spectral expansions on the class of elliptic operators under consideration. If $p\leq 2n/(n-1)$
, whereas the second inequality provides the validity of the localization principle for spectral expansions on the class of elliptic operators under consideration. If $p\leq 2n/(n-1)$![]() , then the second inequality in (1.3) follows from the first one. The claim for the compactness of the support of $f$
, then the second inequality in (1.3) follows from the first one. The claim for the compactness of the support of $f$![]() is stipulated by the fact that then $f$
is stipulated by the fact that then $f$![]() satisfies certain homogeneous boundary conditions depending on the elliptic operator $L$
satisfies certain homogeneous boundary conditions depending on the elliptic operator $L$![]() . The uniform convergence of the spectral expansions only on compact subsets of $G$
. The uniform convergence of the spectral expansions only on compact subsets of $G$![]() is connected with the presence of the boundary $\partial G$
is connected with the presence of the boundary $\partial G$![]() .
.
The main results of this paper are formulated and proved in § 4 and 5. There we study the unconditional convergence of expansions in eigenfunctions of an arbitrary normal elliptic pseudodifferential operator of positive order on a closed smooth manifold $\Gamma$![]() . The convergence is considered with respect to the norm in the Sobolev space $W^{\ell }_{p}(\Gamma )$
. The convergence is considered with respect to the norm in the Sobolev space $W^{\ell }_{p}(\Gamma )$![]() or in the space $C^{\ell }(\Gamma )$
or in the space $C^{\ell }(\Gamma )$![]() , with $p>2$
, with $p>2$![]() and $0\leq \ell \in \mathbb {Z}$
and $0\leq \ell \in \mathbb {Z}$![]() . We find necessary and sufficient conditions for this unconditional convergence to hold true on various classes of differentiable functions and estimate its degree. To this end, we use the Hörmander function classes $H^{\alpha }(\Gamma )$
. We find necessary and sufficient conditions for this unconditional convergence to hold true on various classes of differentiable functions and estimate its degree. To this end, we use the Hörmander function classes $H^{\alpha }(\Gamma )$![]() whose differentiation order is a function $\alpha :[1,\,\infty )\to (0,\,\infty )$
whose differentiation order is a function $\alpha :[1,\,\infty )\to (0,\,\infty )$![]() that O-regularly varies at infinity in the sense of Avakumović. Such classes and their connection with elliptic pseudodifferential operators are discussed in § 3.
that O-regularly varies at infinity in the sense of Avakumović. Such classes and their connection with elliptic pseudodifferential operators are discussed in § 3.
Sections 6 and 7 specify these results for differential operators on the circle and for multiple Fourier series, which allows us to obtain a number of new valuable results for these objects.
Our proofs of the aforementioned results are based on an abstract theorem about the unconditional convergence (see definition 2.1) of expansions in eigenvectors of a normal operator in a space with two norms. This theorem is stated and proved in § 2. It develops and refines known theorems of Krein [Reference Krein23, Theorem 4] and of Krasnosel'skiĭ and Pustyl'nik [Reference Krasnosel'skiĭ, Zabreĭko, Pustyl'nik and Sobolevskiĭ22, Theorem 22.1] with respect to normal operators with pure point spectrum in a Hilbert space.
Final remarks and comments to the obtained results are given in § 8.
2. The basic abstract result
Throughout the paper, we consider complex linear spaces. Let $H$![]() be an infinite-dimensional (not necessarily separable) Hilbert space, and let $N$
be an infinite-dimensional (not necessarily separable) Hilbert space, and let $N$![]() be a normed space. Suppose that $H$
be a normed space. Suppose that $H$![]() and $N$
and $N$![]() are algebraically embedded in a certain linear space. As usual, $\|\cdot \|_{H}$
are algebraically embedded in a certain linear space. As usual, $\|\cdot \|_{H}$![]() and $(\cdot,\,\cdot )_{H}$
and $(\cdot,\,\cdot )_{H}$![]() respectively denote the norm and inner product in $H$
respectively denote the norm and inner product in $H$![]() , and $\|\cdot \|_{N}$
, and $\|\cdot \|_{N}$![]() stands for the norm in $N$
stands for the norm in $N$![]() . Thus, the linear space $H\cap N$
. Thus, the linear space $H\cap N$![]() is endowed with two norms.
is endowed with two norms.
Let $L$![]() be a normal (specifically, self-adjoint) linear operator in $H$
be a normal (specifically, self-adjoint) linear operator in $H$![]() . We allow the case where $L$
. We allow the case where $L$![]() is unbounded in $H$
is unbounded in $H$![]() as well as the case where $L$
as well as the case where $L$![]() is bounded on $H$
is bounded on $H$![]() . We suppose that $L$
. We suppose that $L$![]() has pure point spectrum, i.e. the Hilbert space $H$
has pure point spectrum, i.e. the Hilbert space $H$![]() has an orthonormal basis $\{e_{j}:j\in \Theta \}$
has an orthonormal basis $\{e_{j}:j\in \Theta \}$![]() formed by certain eigenvectors $e_{j}$
formed by certain eigenvectors $e_{j}$![]() of $L$
of $L$![]() . Here, $\Theta$
. Here, $\Theta$![]() is an index set whose cardinality coincides with the Hilbert dimension of $H$
is an index set whose cardinality coincides with the Hilbert dimension of $H$![]() . Thus, every vector $f\in H$
. Thus, every vector $f\in H$![]() expands in the series
expands in the series
in the topology of $H$![]() . (Of course, this series contains only a countable number of non-zero terms, and its sum does not depend on their order.) Let $\lambda _{j}$
. (Of course, this series contains only a countable number of non-zero terms, and its sum does not depend on their order.) Let $\lambda _{j}$![]() denote the eigenvalue of $L$
denote the eigenvalue of $L$![]() such that $Le_j=\lambda _{j}e_j$
such that $Le_j=\lambda _{j}e_j$![]() . As usual, $\sigma (L)$
. As usual, $\sigma (L)$![]() stands for the spectrum of $L$
stands for the spectrum of $L$![]() , and $\sigma _{p}(L)$
, and $\sigma _{p}(L)$![]() denotes the point spectrum of $L$
denotes the point spectrum of $L$![]() , i.e. $\sigma _{p}(L)$
, i.e. $\sigma _{p}(L)$![]() is the set of all eigenvalues of $L$
is the set of all eigenvalues of $L$![]() . Note that eigenvalues of $L$
. Note that eigenvalues of $L$![]() may be of infinite geometric multiplicity and that the set of all eigenvalues of $L$
may be of infinite geometric multiplicity and that the set of all eigenvalues of $L$![]() may have accumulation points.
may have accumulation points.
Let $\mathcal {Q}$![]() denote the system of all finite subsets of $\Theta$
denote the system of all finite subsets of $\Theta$![]() . We interpret $\mathcal {Q}$
. We interpret $\mathcal {Q}$![]() as an upper directed set with respect to the relation $\subseteq$
as an upper directed set with respect to the relation $\subseteq$![]() . Equality (2.1) means for $f\in H$
. Equality (2.1) means for $f\in H$![]() that the net
that the net

converges to $f$![]() in $H$
in $H$![]() .
.
Definition 2.1 Let $f\in H\cap N$![]() . We say that the expansions of $f$
. We say that the expansions of $f$![]() in eigenvectors of $L$
in eigenvectors of $L$![]() converge unconditionally in the normed space $N$
converge unconditionally in the normed space $N$![]() if net (2.2) lies in $N$
if net (2.2) lies in $N$![]() and converges to $f$
and converges to $f$![]() in $N$
in $N$![]() for every orthonormal basis $\{e_{j}:j\in \Theta \}$
for every orthonormal basis $\{e_{j}:j\in \Theta \}$![]() in $H$
in $H$![]() formed by eigenvectors of $L$
formed by eigenvectors of $L$![]() . If this condition is satisfied for every vector $f$
. If this condition is satisfied for every vector $f$![]() from some class $M\subseteq H\cap N$
from some class $M\subseteq H\cap N$![]() , we also say that the expansions in eigenvectors of $L$
, we also say that the expansions in eigenvectors of $L$![]() converge unconditionally in $N$
converge unconditionally in $N$![]() on the class $M$
on the class $M$![]() .
.
Remark 2.2 Providing $H$![]() is separable, eigenvector expansion (2.1) becomes
is separable, eigenvector expansion (2.1) becomes

In this case, the expansions of $f$![]() in eigenvectors of $L$
in eigenvectors of $L$![]() converge unconditionally in $N$
converge unconditionally in $N$![]() if and only if series (2.3) converges to $f$
if and only if series (2.3) converges to $f$![]() in $N$
in $N$![]() for every orthonormal basis $\{e_{j}:j\in \mathbb {N}\}$
for every orthonormal basis $\{e_{j}:j\in \mathbb {N}\}$![]() formed by eigenvectors of $L$
formed by eigenvectors of $L$![]() (i.e. for any choices of orthonormal bases of eigenspaces of $L$
(i.e. for any choices of orthonormal bases of eigenspaces of $L$![]() associated with non-degenerate eigenvalues). It follows from this condition that series (2.3) converges under an arbitrary permutation of its terms.
associated with non-degenerate eigenvalues). It follows from this condition that series (2.3) converges under an arbitrary permutation of its terms.
Theorem 2.3 Let $\omega,\,\eta :\sigma (L)\to \mathbb {C}\setminus \{0\}$![]() be Borel measurable bounded functions, and define the bounded operators $\omega (L)$
be Borel measurable bounded functions, and define the bounded operators $\omega (L)$![]() and $\eta (L)$
and $\eta (L)$![]() on $H$
on $H$![]() as functions of the normal operator $L$
as functions of the normal operator $L$![]() . Assume that the mapping $u\mapsto \omega (L)u$
. Assume that the mapping $u\mapsto \omega (L)u$![]() sets a bounded operator from $H$
sets a bounded operator from $H$![]() to $N$
to $N$![]() , and denote this operator by $R$
, and denote this operator by $R$![]() . Let $f$
. Let $f$![]() be an arbitrary vector from the image of the operator $(\omega \eta )(L)$
be an arbitrary vector from the image of the operator $(\omega \eta )(L)$![]() . Then the expansions of $f$
. Then the expansions of $f$![]() in eigenvectors of $L$
in eigenvectors of $L$![]() converge unconditionally in the space $N$
converge unconditionally in the space $N$![]() . Moreover, the degree of this convergence admits the estimate
. Moreover, the degree of this convergence admits the estimate

for each set $\Upsilon \in \mathcal {Q}$![]() and every orthonormal basis $e:=\{e_{j}:j\in \Theta \}$
and every orthonormal basis $e:=\{e_{j}:j\in \Theta \}$![]() indicated in definition 2.1 and with some net $\{r_{g,e}(\Upsilon ):\Upsilon \in \mathcal {Q}\}\subseteq [0,\,1]$
indicated in definition 2.1 and with some net $\{r_{g,e}(\Upsilon ):\Upsilon \in \mathcal {Q}\}\subseteq [0,\,1]$![]() that tends monotonically to zero and depends neither on $\omega$
that tends monotonically to zero and depends neither on $\omega$![]() nor on $\eta$
nor on $\eta$![]() . Here, $g\in H$
. Here, $g\in H$![]() is the unique vector such that $(\omega \eta )(L)g=f$
is the unique vector such that $(\omega \eta )(L)g=f$![]() .
.
Proof. Since $\omega (L)\eta (L)e_j=(\omega \eta )(\lambda _j)e_j$![]() whenever $j\in \Theta$
whenever $j\in \Theta$![]() and since $(\omega \eta )(t)\neq 0$
and since $(\omega \eta )(t)\neq 0$![]() whenever $t\in \sigma (L)$
whenever $t\in \sigma (L)$![]() , we conclude that each $e_j\in N$
, we conclude that each $e_j\in N$![]() because the image of $\omega (L)$
because the image of $\omega (L)$![]() lies in $N$
lies in $N$![]() . Thus, the left-hand side of (2.4) makes sense. Since the operator $(\omega \eta )(L)$
. Thus, the left-hand side of (2.4) makes sense. Since the operator $(\omega \eta )(L)$![]() is algebraically reversible, the vector $g$
is algebraically reversible, the vector $g$![]() is well defined for every above-mentioned $f$
is well defined for every above-mentioned $f$![]() . Suppose that $f\neq 0$
. Suppose that $f\neq 0$![]() , otherwise the conclusion of this theorem is trivial. Given $\Upsilon \in \mathcal {Q}$
, otherwise the conclusion of this theorem is trivial. Given $\Upsilon \in \mathcal {Q}$![]() , we let $P_{\Upsilon }$
, we let $P_{\Upsilon }$![]() denote the orthoprojector of $H$
denote the orthoprojector of $H$![]() on the span of $\{e_j:j\in \Upsilon \}$
on the span of $\{e_j:j\in \Upsilon \}$![]() and obtain the following estimate:
and obtain the following estimate:

with $I$![]() being the identity operator on $H$
being the identity operator on $H$![]() . We put
. We put
and see that the net $\{r_{g,e}(\Upsilon ):\Upsilon \in \mathcal {Q}\}$![]() is required. Note also that
is required. Note also that
Indeed, since
for every $h\in H$![]() (the convergence holds in $H$
(the convergence holds in $H$![]() ), we have the inequality
), we have the inequality
which gives (2.7). Now (2.5)–(2.7) yield estimate (2.4), which implies the required unconditional convergence.
Remark 2.4 Assume that the norms in $H$![]() and $N$
and $N$![]() are compatible on the linear space $H\cap N$
are compatible on the linear space $H\cap N$![]() . (By definition [Reference Gel'fand and Shilov15, Chapter I, Section 2.2], this compatibility means the following: if a sequence lies in $H\cap N$
. (By definition [Reference Gel'fand and Shilov15, Chapter I, Section 2.2], this compatibility means the following: if a sequence lies in $H\cap N$![]() and converges to zero in one of these norms and is a Cauchy sequence with respect to the second norm, then it converges to zero in the second norm.) Let $R$
and converges to zero in one of these norms and is a Cauchy sequence with respect to the second norm, then it converges to zero in the second norm.) Let $R$![]() be a bounded linear operator on $H$
be a bounded linear operator on $H$![]() (specifically, $R:u\mapsto \omega (L)u$
(specifically, $R:u\mapsto \omega (L)u$![]() where $u\in H$
where $u\in H$![]() , as in theorem 2.3). Then the inclusion $R(H)\subseteq N$
, as in theorem 2.3). Then the inclusion $R(H)\subseteq N$![]() implies that $R$
implies that $R$![]() acts continuously from $H$
acts continuously from $H$![]() to $N$
to $N$![]() . Indeed, suppose that $R(H)\subseteq N$
. Indeed, suppose that $R(H)\subseteq N$![]() . Then, owing to the closed graph theorem, the operator $R:H\to \widetilde {N}$
. Then, owing to the closed graph theorem, the operator $R:H\to \widetilde {N}$![]() is bounded if and only if it is closed; here, $\widetilde {N}$
is bounded if and only if it is closed; here, $\widetilde {N}$![]() is the completion of the normed space $N$
is the completion of the normed space $N$![]() . We therefore have to prove that this operator is closable. Assume that a sequence $(u_{k})_{k=1}^{\infty }\subset H$
. We therefore have to prove that this operator is closable. Assume that a sequence $(u_{k})_{k=1}^{\infty }\subset H$![]() satisfies the following two conditions: $u_{k}\to 0$
satisfies the following two conditions: $u_{k}\to 0$![]() in $H$
in $H$![]() and
and
as $k\to \infty$![]() . Then $Ru_{k}\to 0$
. Then $Ru_{k}\to 0$![]() in $H$
in $H$![]() because $R$
because $R$![]() is bounded on $H$
is bounded on $H$![]() . Besides, $(Ru_{k})_{k=1}^{\infty }$
. Besides, $(Ru_{k})_{k=1}^{\infty }$![]() is a Cauchy sequence in $N$
is a Cauchy sequence in $N$![]() . Hence, $Ru_{k}\to 0$
. Hence, $Ru_{k}\to 0$![]() in $N$
in $N$![]() because the norms in $N$
because the norms in $N$![]() and $H$
and $H$![]() are compatible on $H\cap N$
are compatible on $H\cap N$![]() . Thus, $v=0$
. Thus, $v=0$![]() in view of (2.8), which means that the operator $R:H\to \widetilde {N}$
in view of (2.8), which means that the operator $R:H\to \widetilde {N}$![]() is closable.
is closable.
Theorem 2.3 contains Krein's result [Reference Krein23, Theorem 4] according to which series (2.3) converges in $N$![]() for every $f\in L(H)$
for every $f\in L(H)$![]() if $L$
if $L$![]() is a compact self-adjoint operator in $H$
is a compact self-adjoint operator in $H$![]() and if $L$
and if $L$![]() acts continuously from $H$
acts continuously from $H$![]() to a Banach space $N$
to a Banach space $N$![]() . The latter theorem generalizes (to abstract operators) the Hilbert–Schmidt theorem about the uniform decomposability of sourcewise representable functions in eigenfunctions of a symmetric integral operator.
. The latter theorem generalizes (to abstract operators) the Hilbert–Schmidt theorem about the uniform decomposability of sourcewise representable functions in eigenfunctions of a symmetric integral operator.
If $L$![]() is a positive definite self-adjoint operator with discrete spectrum and if $\omega (t)\equiv t^{-\delta }$
is a positive definite self-adjoint operator with discrete spectrum and if $\omega (t)\equiv t^{-\delta }$![]() and $\eta (t)\equiv t^{-\tau }$
and $\eta (t)\equiv t^{-\tau }$![]() for certain numbers $\delta,\,\tau \geq 0$
for certain numbers $\delta,\,\tau \geq 0$![]() and if $R:=L^{-\delta }$
and if $R:=L^{-\delta }$![]() acts continuously from $H$
acts continuously from $H$![]() to a Banach space $N$
to a Banach space $N$![]() , Krasnosel'skiĭ and Pustyl'nik [Reference Krasnosel'skiĭ, Zabreĭko, Pustyl'nik and Sobolevskiĭ22, Theorem 22.1] proved that
, Krasnosel'skiĭ and Pustyl'nik [Reference Krasnosel'skiĭ, Zabreĭko, Pustyl'nik and Sobolevskiĭ22, Theorem 22.1] proved that

for any $f$![]() from the domain of $L^{\delta +\tau }$
from the domain of $L^{\delta +\tau }$![]() (the Hilbert space $H$
(the Hilbert space $H$![]() is assumed to be separable). Here, the eigenvalues $\lambda _{k}>0$
is assumed to be separable). Here, the eigenvalues $\lambda _{k}>0$![]() of $L$
of $L$![]() are numbered so that $\lambda _{k}\leq \lambda _{k+1}$
are numbered so that $\lambda _{k}\leq \lambda _{k+1}$![]() . Formula (2.4) implies a more general result for normal operators with discrete spectrum.
. Formula (2.4) implies a more general result for normal operators with discrete spectrum.
3. Hörmander spaces and elliptic operators
We will use them to estimate the degree of the convergence of expansions in eigenfunctions of some elliptic operators given on a closed manifold. Such spaces were introduced over $\mathbb {R}^{n}$![]() and investigated by Hörmander [Reference Hörmander17, Section 2.2]. Their smoothness index (or differentiation order) is a general enough function of the frequency variables, which allows us to obtain finer estimates than those [Reference Agranovich1, Subsection 6.1 a] received with the help of classical function spaces such as Sobolev spaces, whose smoothness index is a number. We use a broad class of isotropic inner product Hörmander spaces that admit a reasonable definition on smooth closed manifolds. The class was introduced and investigated in [Reference Mikhailets and Murach27], [Reference Mikhailets and Murach28, Section 2.4.2] and [Reference Mikhailets and Murach29] (note that these works develop an approach proposed in [Reference Mikhailets and Murach25, Reference Mikhailets and Murach26]). It has various applications to elliptic operators [Reference Mikhailets and Murach28, Section 2.4.3] and elliptic boundary-value problems [Reference Anop, Chepurukhina and Murach4, Reference Anop, Denk and Murach5].
and investigated by Hörmander [Reference Hörmander17, Section 2.2]. Their smoothness index (or differentiation order) is a general enough function of the frequency variables, which allows us to obtain finer estimates than those [Reference Agranovich1, Subsection 6.1 a] received with the help of classical function spaces such as Sobolev spaces, whose smoothness index is a number. We use a broad class of isotropic inner product Hörmander spaces that admit a reasonable definition on smooth closed manifolds. The class was introduced and investigated in [Reference Mikhailets and Murach27], [Reference Mikhailets and Murach28, Section 2.4.2] and [Reference Mikhailets and Murach29] (note that these works develop an approach proposed in [Reference Mikhailets and Murach25, Reference Mikhailets and Murach26]). It has various applications to elliptic operators [Reference Mikhailets and Murach28, Section 2.4.3] and elliptic boundary-value problems [Reference Anop, Chepurukhina and Murach4, Reference Anop, Denk and Murach5].
This class is formed by certain function spaces $H^{\alpha }$![]() whose smoothness index $\alpha$
whose smoothness index $\alpha$![]() ranges over a set denoted by $\mathrm {OR}$
ranges over a set denoted by $\mathrm {OR}$![]() . By definition, $\mathrm {OR}$
. By definition, $\mathrm {OR}$![]() consists of all Borel functions $\alpha : [1,\,\infty )\rightarrow (0,\,\infty )$
consists of all Borel functions $\alpha : [1,\,\infty )\rightarrow (0,\,\infty )$![]() such that
such that
with the numbers $b>1$![]() and $c\geq 1$
and $c\geq 1$![]() being independent of $t$
being independent of $t$![]() and $\lambda$
and $\lambda$![]() (but may depend on $\alpha$
(but may depend on $\alpha$![]() ). Such functions were introduced by Avakumović [Reference Avakumović7], are called OR-varying (or O-regularly varying) at infinity, and are well investigated [Reference Bingham, Goldie and Teugels9, Reference Buldygin, Indlekofer, Klesov and Steinebach10].
). Such functions were introduced by Avakumović [Reference Avakumović7], are called OR-varying (or O-regularly varying) at infinity, and are well investigated [Reference Bingham, Goldie and Teugels9, Reference Buldygin, Indlekofer, Klesov and Steinebach10].
The class $\mathrm {OR}$![]() admits the following description [Reference Bingham, Goldie and Teugels9, Theorem 2.2.7]: $\alpha \in \mathrm {OR}$
admits the following description [Reference Bingham, Goldie and Teugels9, Theorem 2.2.7]: $\alpha \in \mathrm {OR}$![]() if and only if
if and only if

for some bounded Borel functions $\beta,\,\gamma :[1,\,\infty )\to \mathbb {R}$![]() .
.
For every function $\alpha \in \mathrm {OR}$![]() there exist numbers $s_{0},\,s_{1}\in \mathbb {R}$
there exist numbers $s_{0},\,s_{1}\in \mathbb {R}$![]() , with $s_{0}\leq s_{1}$
, with $s_{0}\leq s_{1}$![]() , and numbers $c_{0},\,c_{1}>0$
, and numbers $c_{0},\,c_{1}>0$![]() such that
such that
Given $\alpha \in \mathrm {OR}$![]() , we let $s_{\ast }(\alpha )$
, we let $s_{\ast }(\alpha )$![]() denote the supremum of the set of all numbers $s_{0}$
denote the supremum of the set of all numbers $s_{0}$![]() that the left-hand inequality in (3.2) holds true (for certain $c_{0}$
that the left-hand inequality in (3.2) holds true (for certain $c_{0}$![]() depending on $s_{0}$
depending on $s_{0}$![]() ), and we let $s^{\ast }(\alpha )$
), and we let $s^{\ast }(\alpha )$![]() denote the infimum of the set of all numbers $s_{1}$
denote the infimum of the set of all numbers $s_{1}$![]() that the right-hand inequality in (3.2) holds true (for certain $c_{1}$
that the right-hand inequality in (3.2) holds true (for certain $c_{1}$![]() depending on $s_{1}$
depending on $s_{1}$![]() ). Of course, $-\infty < s_{\ast }(\alpha )\leq s^{\ast }(\alpha )<\infty$
). Of course, $-\infty < s_{\ast }(\alpha )\leq s^{\ast }(\alpha )<\infty$![]() . The numbers $s_{\ast }(\alpha )$
. The numbers $s_{\ast }(\alpha )$![]() and $s^{\ast }(\alpha )$
and $s^{\ast }(\alpha )$![]() are equal to the lower and upper Orlicz–Matuszewska indices of $\alpha$
are equal to the lower and upper Orlicz–Matuszewska indices of $\alpha$![]() , resp. These facts follow from [Reference Bingham, Goldie and Teugels9, Theorem 2.1.7 and Proposition 2.2.1].
, resp. These facts follow from [Reference Bingham, Goldie and Teugels9, Theorem 2.1.7 and Proposition 2.2.1].
For instance, every continuous function $\alpha :[1,\,\infty )\rightarrow (0,\,\infty )$![]() such that
such that
belongs to $\mathrm {OR}$![]() ; here, $1\leq k\in \mathbb {Z}$
; here, $1\leq k\in \mathbb {Z}$![]() and $s,\,s_{1},\,\ldots,\,s_{k}\in \mathbb {R}$
and $s,\,s_{1},\,\ldots,\,s_{k}\in \mathbb {R}$![]() . It is well known that $s_{\ast }(\alpha )=s^{\ast }(\alpha )=s$
. It is well known that $s_{\ast }(\alpha )=s^{\ast }(\alpha )=s$![]() for this function.
for this function.
An example of a function $\alpha \in \mathrm {OR}$![]() with the different Orlicz–Matuszewska indices is given by formula (3.1) in which
with the different Orlicz–Matuszewska indices is given by formula (3.1) in which
provided that $r< s$![]() , $1=\theta _{1}<\theta _{2}<\theta _{3}<\dots$
, $1=\theta _{1}<\theta _{2}<\theta _{3}<\dots$![]() , and $\theta _{k}\to \infty$
, and $\theta _{k}\to \infty$![]() as $k\to \infty$
as $k\to \infty$![]() . Then ${s_{\ast }(\alpha )=r}$
. Then ${s_{\ast }(\alpha )=r}$![]() and $s^{\ast }(\alpha )=s$
and $s^{\ast }(\alpha )=s$![]() , as is noticed, e.g., in [Reference Anop, Chepurukhina and Murach4, Section 3].
, as is noticed, e.g., in [Reference Anop, Chepurukhina and Murach4, Section 3].
Let $\alpha \in \mathrm {OR}$![]() and $1\leq n\in \mathbb {Z}$
and $1\leq n\in \mathbb {Z}$![]() . By definition, the linear space $H^{\alpha }(\mathbb {R}^{n})$
. By definition, the linear space $H^{\alpha }(\mathbb {R}^{n})$![]() consists of all tempered distributions $w$
consists of all tempered distributions $w$![]() on $\mathbb {R}^{n}$
on $\mathbb {R}^{n}$![]() that their Fourier transform $\widehat {w}:=\mathcal {F}w$
that their Fourier transform $\widehat {w}:=\mathcal {F}w$![]() is locally Lebesgue integrable over $\mathbb {R}^{n}$
is locally Lebesgue integrable over $\mathbb {R}^{n}$![]() and satisfies the condition
and satisfies the condition

As usual, $\langle \xi \rangle :=(1+|\xi |^{2})^{1/2}$![]() is the smoothed absolute value of $\xi \in \mathbb {R}^{n}$
is the smoothed absolute value of $\xi \in \mathbb {R}^{n}$![]() . The space $H^{\alpha }(\mathbb {R}^{n})$
. The space $H^{\alpha }(\mathbb {R}^{n})$![]() is endowed with the inner product
is endowed with the inner product

and the corresponding norm. This space is an isotropic Hilbert case of the Hörmander spaces $\mathcal {B}_{p,k}$![]() considered in [Reference Hörmander17, Section 2.2] and [Reference Hörmander18, Section 10.1]. Namely, $H^{\alpha }(\mathbb {R}^{n})=\mathcal {B}_{2,k}$
considered in [Reference Hörmander17, Section 2.2] and [Reference Hörmander18, Section 10.1]. Namely, $H^{\alpha }(\mathbb {R}^{n})=\mathcal {B}_{2,k}$![]() provided that $k(\xi )=\alpha (\langle \xi \rangle )$
provided that $k(\xi )=\alpha (\langle \xi \rangle )$![]() whenever $\xi \in \mathbb {R}^{n}$
whenever $\xi \in \mathbb {R}^{n}$![]() .
.
Consider a version of the space $H^{\alpha }(\mathbb {R}^{n})$![]() for smooth closed manifolds. In the sequel, $\Gamma$
for smooth closed manifolds. In the sequel, $\Gamma$![]() is a closed (i.e. compact and boundaryless) manifold of dimension $n\geq 1$
is a closed (i.e. compact and boundaryless) manifold of dimension $n\geq 1$![]() and class $C^{\infty }$
and class $C^{\infty }$![]() . Suppose that a positive $C^{\infty }$
. Suppose that a positive $C^{\infty }$![]() -density ${\rm d}x$
-density ${\rm d}x$![]() is given on $\Gamma$
is given on $\Gamma$![]() . We arbitrarily choose a finite atlas from the $C^{\infty }$
. We arbitrarily choose a finite atlas from the $C^{\infty }$![]() -structure on $\Gamma$
-structure on $\Gamma$![]() ; let this atlas be formed by $\varkappa$
; let this atlas be formed by $\varkappa$![]() local charts $\pi _{j}: \mathbb {R}^{n}\leftrightarrow \Gamma _{j}$
local charts $\pi _{j}: \mathbb {R}^{n}\leftrightarrow \Gamma _{j}$![]() , with $j=1,\,\ldots,\,\varkappa$
, with $j=1,\,\ldots,\,\varkappa$![]() . Here, the open sets $\Gamma _{1},\,\ldots,\,\Gamma _{\varkappa }$
. Here, the open sets $\Gamma _{1},\,\ldots,\,\Gamma _{\varkappa }$![]() form a covering of $\Gamma$
form a covering of $\Gamma$![]() . We also arbitrarily choose functions $\chi _j\in C^{\infty }(\Gamma )$
. We also arbitrarily choose functions $\chi _j\in C^{\infty }(\Gamma )$![]() , with $j=1,\,\ldots,\,\varkappa$
, with $j=1,\,\ldots,\,\varkappa$![]() , such that $\chi _{1}(x)+\cdots +\chi _{\varkappa }(x)=1$
, such that $\chi _{1}(x)+\cdots +\chi _{\varkappa }(x)=1$![]() whenever $x\in \Gamma$
whenever $x\in \Gamma$![]() and that $\mathrm {supp}\,\chi _j\subset \Gamma _j$
and that $\mathrm {supp}\,\chi _j\subset \Gamma _j$![]() whenever $1\leq j\leq \varkappa$
whenever $1\leq j\leq \varkappa$![]() . Thus, these functions form a partition of unity on $\Gamma$
. Thus, these functions form a partition of unity on $\Gamma$![]() subordinate to the above covering.
subordinate to the above covering.
By definition, the linear space $H^{\alpha }(\Gamma )$![]() consists of all distributions $f$
consists of all distributions $f$![]() on $\Gamma$
on $\Gamma$![]() such that $(\chi _{j}f)\circ \pi _{j}\in H^{\alpha }(\mathbb {R}^{n})$
such that $(\chi _{j}f)\circ \pi _{j}\in H^{\alpha }(\mathbb {R}^{n})$![]() for each $j\in \{1,\,\ldots,\,\varkappa \}$
for each $j\in \{1,\,\ldots,\,\varkappa \}$![]() . Here, $(\chi _{j}f)\circ \pi _{j}$
. Here, $(\chi _{j}f)\circ \pi _{j}$![]() is the representation of the distribution $\chi _{j}f$
is the representation of the distribution $\chi _{j}f$![]() in the local chart $\pi _{j}$
in the local chart $\pi _{j}$![]() . The space $H^{\alpha }(\Gamma )$
. The space $H^{\alpha }(\Gamma )$![]() is endowed with the inner product
is endowed with the inner product

and the corresponding norm $\|f\|_{H,\alpha }:=(f,\,f)_{H,\alpha }^{1/2}$![]() . This space is complete (i.e. Hilbert) and separable and does not depend up to equivalence of norms on the choice of the atlas and partition of unity on $\Gamma$
. This space is complete (i.e. Hilbert) and separable and does not depend up to equivalence of norms on the choice of the atlas and partition of unity on $\Gamma$![]() ; the set $C^{\infty }(\Gamma )$
; the set $C^{\infty }(\Gamma )$![]() is dense in $H^{\alpha }(\Gamma )$
is dense in $H^{\alpha }(\Gamma )$![]() . These properties are due to [Reference Mikhailets and Murach28, Theorem 2.21].
. These properties are due to [Reference Mikhailets and Murach28, Theorem 2.21].
If $\alpha (t)\equiv t^{s}$![]() for some $s\in \mathbb {R}$
for some $s\in \mathbb {R}$![]() , then $H^{\alpha }(G)$
, then $H^{\alpha }(G)$![]() , where $G=\mathbb {R}^{n}$
, where $G=\mathbb {R}^{n}$![]() or $G=\Gamma$
or $G=\Gamma$![]() , becomes the inner product Sobolev space $W^{s}_{2}(G)$
, becomes the inner product Sobolev space $W^{s}_{2}(G)$![]() of order $s$
of order $s$![]() .
.
We also need an equivalent definition of the space $H^{\alpha }(\Gamma )$![]() , with $\alpha \in \mathrm {OR}$
, with $\alpha \in \mathrm {OR}$![]() , in terms of a function of some elliptic pseudodifferential operators (PsDOs). Following [Reference Agranovich1, Section 2.1], we let $\Psi _{\mathrm {ph}}^{m}(\Gamma )$
, in terms of a function of some elliptic pseudodifferential operators (PsDOs). Following [Reference Agranovich1, Section 2.1], we let $\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() denote the class of all classical (i.e. polyhomogeneous) PsDOs on $\Gamma$
denote the class of all classical (i.e. polyhomogeneous) PsDOs on $\Gamma$![]() of order $m\in \mathbb {R}$
of order $m\in \mathbb {R}$![]() . Suppose that $m>0$
. Suppose that $m>0$![]() and that a PsDO $A\in \Psi _{\mathrm {ph}}^{m}(\Gamma )$
and that a PsDO $A\in \Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() is elliptic on $\Gamma$
is elliptic on $\Gamma$![]() , i.e. $a_{0}(x,\,\xi )\neq 0$
, i.e. $a_{0}(x,\,\xi )\neq 0$![]() whenever $x\in \Gamma$
whenever $x\in \Gamma$![]() and $0\neq \xi \in T_{x}^{\ast }\Gamma$
and $0\neq \xi \in T_{x}^{\ast }\Gamma$![]() , with $a_{0}(x,\,\xi )$
, with $a_{0}(x,\,\xi )$![]() denoting the principal symbol of $A$
denoting the principal symbol of $A$![]() and with $T_{x}^{\ast }\Gamma$
and with $T_{x}^{\ast }\Gamma$![]() standing (as usual) for the cotangent space to $\Gamma$
standing (as usual) for the cotangent space to $\Gamma$![]() at $x$
at $x$![]() . We may and will consider $A$
. We may and will consider $A$![]() as a closed unbounded operator in the Hilbert Lebesgue space $L_{2}(\Gamma ):=L_{2}(\Gamma,\,{\rm d}x)$
as a closed unbounded operator in the Hilbert Lebesgue space $L_{2}(\Gamma ):=L_{2}(\Gamma,\,{\rm d}x)$![]() and with the domain $\mathrm {Dom}\,A=W^{m}_{2}(\Gamma )$
and with the domain $\mathrm {Dom}\,A=W^{m}_{2}(\Gamma )$![]() (see [Reference Agranovich1, Theorem 2.3.5]). Suppose that $A$
(see [Reference Agranovich1, Theorem 2.3.5]). Suppose that $A$![]() is a self-adjoint operator in $L_{2}(\Gamma )$
is a self-adjoint operator in $L_{2}(\Gamma )$![]() and that $\sigma (A)\subseteq [1,\,\infty )$
and that $\sigma (A)\subseteq [1,\,\infty )$![]() . Then the operator $\alpha (A^{1/m})$
. Then the operator $\alpha (A^{1/m})$![]() is well defined in the Hilbert space $L_{2}(\Gamma,\,{\rm d}x)$
is well defined in the Hilbert space $L_{2}(\Gamma,\,{\rm d}x)$![]() via Spectral Theorem as the Borel function $\alpha (t^{1/m})$
via Spectral Theorem as the Borel function $\alpha (t^{1/m})$![]() of $A$
of $A$![]() .
.
Proposition 3.1 Let $\alpha \in \mathrm {OR}$![]() . Then the norm in the space $H^{\alpha }(\Gamma )$
. Then the norm in the space $H^{\alpha }(\Gamma )$![]() is equivalent to the norm
is equivalent to the norm
on the dense set $C^{\infty }(\Gamma )$![]() . Thus, $H^{\alpha }(\Gamma )$
. Thus, $H^{\alpha }(\Gamma )$![]() coincides with the completion of $C^{\infty }(\Gamma )$
coincides with the completion of $C^{\infty }(\Gamma )$![]() with respect to norm (3.4). Hence, if the function $1/\alpha$
with respect to norm (3.4). Hence, if the function $1/\alpha$![]() is bounded on $[1,\,\infty )$
is bounded on $[1,\,\infty )$![]() , then $H^{\alpha }(\Gamma )$
, then $H^{\alpha }(\Gamma )$![]() is the domain of the operator $\alpha (A^{1/m})$
is the domain of the operator $\alpha (A^{1/m})$![]() and this operator sets an isomorphism between $H^{\alpha }(\Gamma )$
and this operator sets an isomorphism between $H^{\alpha }(\Gamma )$![]() and $L_{2}(\Gamma )$
and $L_{2}(\Gamma )$![]() .
.
This proposition is due to [Reference Mikhailets and Murach28, Theorem 2.23]. We may put $A:=1-\Delta _{\Gamma }$![]() and $m=2$
and $m=2$![]() , where $\Delta _{\Gamma }$
, where $\Delta _{\Gamma }$![]() is the Laplace–Beltrami operator on $\Gamma$
is the Laplace–Beltrami operator on $\Gamma$![]() , with $\Gamma$
, with $\Gamma$![]() being endowed with the Riemannian metric inducing ${\rm d}x$
being endowed with the Riemannian metric inducing ${\rm d}x$![]() .
.
4. Mean convergence
Given $s\in \mathbb {R}$![]() and $p\in (1,\,\infty )$
and $p\in (1,\,\infty )$![]() , we let $W^{s}_{p}(\Gamma )$
, we let $W^{s}_{p}(\Gamma )$![]() denote the Sobolev space over $\Gamma$
denote the Sobolev space over $\Gamma$![]() with the smoothness index $s$
with the smoothness index $s$![]() and the integral-exponent $p$
and the integral-exponent $p$![]() and let $\|\cdot \|_{W,s,p}$
and let $\|\cdot \|_{W,s,p}$![]() stand for the norm in this space. The space $W^{s}_{p}(\Gamma )$
stand for the norm in this space. The space $W^{s}_{p}(\Gamma )$![]() is defined on the base of $W^{s}_{p}(\mathbb {R}^{n})$
is defined on the base of $W^{s}_{p}(\mathbb {R}^{n})$![]() with the help of the above atlas and partition of unity like the definition of $H^{\alpha }(\Gamma )$
with the help of the above atlas and partition of unity like the definition of $H^{\alpha }(\Gamma )$![]() on the base of $H^{\alpha }(\mathbb {R}^{n})$
on the base of $H^{\alpha }(\mathbb {R}^{n})$![]() . Recall that the Sobolev space $W^{s}_{p}(\mathbb {R}^{n})$
. Recall that the Sobolev space $W^{s}_{p}(\mathbb {R}^{n})$![]() consists of all tempered distributions $w$
consists of all tempered distributions $w$![]() on $\mathbb {R}^{n}$
on $\mathbb {R}^{n}$![]() such that the distribution $v:=\mathcal {F}^{-1}[\langle \xi \rangle ^{s}\,\widehat {w}(\xi )]$
such that the distribution $v:=\mathcal {F}^{-1}[\langle \xi \rangle ^{s}\,\widehat {w}(\xi )]$![]() belongs to the Lebesgue space $L_{p}(\mathbb {R}^{n})$
belongs to the Lebesgue space $L_{p}(\mathbb {R}^{n})$![]() , with the norm of $w$
, with the norm of $w$![]() in $W^{s}_{p}(\mathbb {R}^{n})$
in $W^{s}_{p}(\mathbb {R}^{n})$![]() being equal to the norm of $v$
being equal to the norm of $v$![]() in $L_{p}(\mathbb {R}^{n})$
in $L_{p}(\mathbb {R}^{n})$![]() . Of course, $\mathcal {F}^{-1}$
. Of course, $\mathcal {F}^{-1}$![]() stands for the inverse Fourier transform. Note that $W^{0}_{p}(\Gamma )$
stands for the inverse Fourier transform. Note that $W^{0}_{p}(\Gamma )$![]() coincides with the Lebesgue space $L_{p}(\Gamma ):=L_{p}(\Gamma,\,{\rm d}x)$
coincides with the Lebesgue space $L_{p}(\Gamma ):=L_{p}(\Gamma,\,{\rm d}x)$![]() , and assume that this holds with equality of norms.
, and assume that this holds with equality of norms.
We use the term ‘mean convergence’ to refer to the convergence in the normed Sobolev space $W^{\ell }_{p}(\Gamma )$![]() subject to $0\leq \ell \in \mathbb {Z}$
subject to $0\leq \ell \in \mathbb {Z}$![]() and $1< p<\infty$
and $1< p<\infty$![]() , specifically in the Lebesgue space $L_{p}(\Gamma )$
, specifically in the Lebesgue space $L_{p}(\Gamma )$![]() .
.
Let real $m>0$![]() , and let $A\in \Psi _{\mathrm {ph}}^{m}(\Gamma )$
, and let $A\in \Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() . Suppose that the PsDO $A$
. Suppose that the PsDO $A$![]() is elliptic on $\Gamma$
is elliptic on $\Gamma$![]() . If $A$
. If $A$![]() is a normal operator in $L_{2}(\Gamma )$
is a normal operator in $L_{2}(\Gamma )$![]() , the separable Hilbert space $L_{2}(\Gamma )$
, the separable Hilbert space $L_{2}(\Gamma )$![]() has an orthonormal basis formed by some eigenfunctions of $A$
has an orthonormal basis formed by some eigenfunctions of $A$![]() (see e.g. [Reference Shubin32, Section 15.3]), every eigenfunction of $A$
(see e.g. [Reference Shubin32, Section 15.3]), every eigenfunction of $A$![]() pertaining to $C^{\infty }(\Gamma )$
pertaining to $C^{\infty }(\Gamma )$![]() and each eigenvalue of $A$
and each eigenvalue of $A$![]() being of finite multiplicity. Then every vector $f\in L_{2}(\Gamma )$
being of finite multiplicity. Then every vector $f\in L_{2}(\Gamma )$![]() admits the spectral decomposition
admits the spectral decomposition

the series converging in $L_{2}(\Gamma )$![]() . As usual, $P(\lambda )$
. As usual, $P(\lambda )$![]() denotes the orthoprojector on the eigenspace of $A$
denotes the orthoprojector on the eigenspace of $A$![]() associated with the eigenvalue $\lambda$
associated with the eigenvalue $\lambda$![]() . Note that the sum in (4.1) contains only a finite number of terms for every $r>0$
. Note that the sum in (4.1) contains only a finite number of terms for every $r>0$![]() . The convergence in $L_{2}(\Gamma )$
. The convergence in $L_{2}(\Gamma )$![]() implies one in each normed space $L_{p}(\Gamma )$
implies one in each normed space $L_{p}(\Gamma )$![]() with $1\leq p<2$
with $1\leq p<2$![]() ; hence, we are interested in conditions for the convergence of (4.1) in the mean with index $p>2$
; hence, we are interested in conditions for the convergence of (4.1) in the mean with index $p>2$![]() .
.
Given real $m>0$![]() , we let $\mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
, we let $\mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() denote the set of all PsDOs of class $\Psi _{\mathrm {ph}}^{m}(\Gamma )$
denote the set of all PsDOs of class $\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() that are elliptic on $\Gamma$
that are elliptic on $\Gamma$![]() and normal in $L_{2}(\Gamma )$
and normal in $L_{2}(\Gamma )$![]() . Specifically, every elliptic constant-coefficient partial differential operator on $\Gamma$
. Specifically, every elliptic constant-coefficient partial differential operator on $\Gamma$![]() of order $m$
of order $m$![]() belongs to $\mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
belongs to $\mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() . Recall that $n=\dim \Gamma \geq 1$
. Recall that $n=\dim \Gamma \geq 1$![]() .
.
Theorem 4.1 Suppose that $0< m\in \mathbb {R}$![]() , $0\leq \ell \in \mathbb {Z}$
, $0\leq \ell \in \mathbb {Z}$![]() , $s,\,p,\,q\in \mathbb {R}$
, $s,\,p,\,q\in \mathbb {R}$![]() and $1< q\leq 2< p$
and $1< q\leq 2< p$![]() . Then the following three conditions are equivalent:
. Then the following three conditions are equivalent:
(i) $s\geq \ell +n/q-n/p$
 ;
;(ii) there exists a PsDO $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
 that spectral decomposition (4.1) induced by $A$
that spectral decomposition (4.1) induced by $A$ converges in $W^{\ell }_{p}(\Gamma )$
converges in $W^{\ell }_{p}(\Gamma )$ on the class $W^{s}_{q}(\Gamma )$
on the class $W^{s}_{q}(\Gamma )$ ;
;(iii) the expansions in eigenfunctions of an arbitrary PsDO from $\mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
 converge unconditionally in $W^{\ell }_{p}(\Gamma )$
converge unconditionally in $W^{\ell }_{p}(\Gamma )$ on the class $W^{s}_{q}(\Gamma )$
on the class $W^{s}_{q}(\Gamma )$ .
.
Proof. We will first prove that $\mathrm {(i)}\Rightarrow \mathrm {(iii)}$![]() . Assuming (i) to hold true, we arbitrarily choose a PsDO $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
. Assuming (i) to hold true, we arbitrarily choose a PsDO $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() and put $L:=(I+A^{\ast }A)$
and put $L:=(I+A^{\ast }A)$![]() , with $I$
, with $I$![]() denoting the identity operator on $L_{2}(\Gamma )$
denoting the identity operator on $L_{2}(\Gamma )$![]() . Let $\sigma :=\ell +n/2-n/p>0$
. Let $\sigma :=\ell +n/2-n/p>0$![]() . Since $L\in \mathrm {NE}\Psi _{\mathrm {ph}}^{2m}(\Gamma )$
. Since $L\in \mathrm {NE}\Psi _{\mathrm {ph}}^{2m}(\Gamma )$![]() and $\sigma (L)\subseteq [1,\,\infty )$
and $\sigma (L)\subseteq [1,\,\infty )$![]() , the operator $L^{\sigma /(2m)}$
, the operator $L^{\sigma /(2m)}$![]() is well defined in $L_{2}(\Gamma )$
is well defined in $L_{2}(\Gamma )$![]() as a power function of $L$
as a power function of $L$![]() and sets an isomorphism between $W^{\sigma }_{2}(\Gamma )$
and sets an isomorphism between $W^{\sigma }_{2}(\Gamma )$![]() and $L_{2}(\Gamma )$
and $L_{2}(\Gamma )$![]() ; see [Reference Agranovich1, Corollary 5.3.2]. The inverse of $L$
; see [Reference Agranovich1, Corollary 5.3.2]. The inverse of $L$![]() , i.e. the operator $L^{-\sigma /(2m)}$
, i.e. the operator $L^{-\sigma /(2m)}$![]() , acts continuously from $H=L_{2}(\Gamma )$
, acts continuously from $H=L_{2}(\Gamma )$![]() to $N:=W^{\ell }_{p}(\Gamma )$
to $N:=W^{\ell }_{p}(\Gamma )$![]() because of the continuous embedding $W^{\sigma }_{2}(\Gamma )\hookrightarrow W^{\ell }_{p}(\Gamma )$
because of the continuous embedding $W^{\sigma }_{2}(\Gamma )\hookrightarrow W^{\ell }_{p}(\Gamma )$![]() . This embedding follows directly from its well-known analogue for Sobolev spaces over $\mathbb {R}^{n}$
. This embedding follows directly from its well-known analogue for Sobolev spaces over $\mathbb {R}^{n}$![]() (see e.g. [Reference Triebel33, Theorem 2.8.1(b)]). Using theorem 2.3, we put $\omega (t):=t^{-\sigma /(2m)}$
(see e.g. [Reference Triebel33, Theorem 2.8.1(b)]). Using theorem 2.3, we put $\omega (t):=t^{-\sigma /(2m)}$![]() and $\eta (t):=1$
and $\eta (t):=1$![]() whenever $t\geq 1$
whenever $t\geq 1$![]() and remark that $W^{\sigma }_{2}(\Gamma )$
and remark that $W^{\sigma }_{2}(\Gamma )$![]() is the image of the operator $(\omega \eta )(L)$
is the image of the operator $(\omega \eta )(L)$![]() . We conclude by this theorem that the expansions in eigenfunctions of $L$
. We conclude by this theorem that the expansions in eigenfunctions of $L$![]() converge unconditionally in $W^{\ell }_{p}(\Gamma )$
converge unconditionally in $W^{\ell }_{p}(\Gamma )$![]() on the class $W^{\sigma }_{2}(\Gamma )$
on the class $W^{\sigma }_{2}(\Gamma )$![]() . Observe that $W^{s}_{q}(\Gamma )\hookrightarrow W^{\sigma }_{2}(\Gamma )$
. Observe that $W^{s}_{q}(\Gamma )\hookrightarrow W^{\sigma }_{2}(\Gamma )$![]() because $s\geq \sigma +n/q-n/2$
because $s\geq \sigma +n/q-n/2$![]() by (i). This yields (iii) since all eigenfunctions of $A$
by (i). This yields (iii) since all eigenfunctions of $A$![]() are eigenfunctions of $L$
are eigenfunctions of $L$![]() as well. We have proved that $\mathrm {(i)}\Rightarrow \mathrm {(iii)}$
as well. We have proved that $\mathrm {(i)}\Rightarrow \mathrm {(iii)}$![]() .
.
The implication $\mathrm {(iii)}\Rightarrow \mathrm {(ii)}$![]() is obvious.
is obvious.
It remains to prove that $\mathrm {(ii)}\Rightarrow \mathrm {(i)}$![]() . Assuming (ii) to hold true, we obtain the embedding of $W^{s}_{q}(\Gamma )$
. Assuming (ii) to hold true, we obtain the embedding of $W^{s}_{q}(\Gamma )$![]() in $W^{\ell }_{p}(\Gamma )$
in $W^{\ell }_{p}(\Gamma )$![]() . The embedding implies (i), which is considered to be a known fact. Specifically, this fact follows from [Reference Triebel34, p. 60, property (ii)]. Namely, the above embedding implies that $W^{s}_{q}(G)\hookrightarrow W^{\ell }_{p}(G)$
. The embedding implies (i), which is considered to be a known fact. Specifically, this fact follows from [Reference Triebel34, p. 60, property (ii)]. Namely, the above embedding implies that $W^{s}_{q}(G)\hookrightarrow W^{\ell }_{p}(G)$![]() for any open ball $G$
for any open ball $G$![]() in $\mathbb {R}^{n}$
in $\mathbb {R}^{n}$![]() . (Recall that $W^{s}_{q}(G)$
. (Recall that $W^{s}_{q}(G)$![]() , e.g. consists of the restrictions of all distributions $w\in W^{s}_{q}(\mathbb {R}^{n})$
, e.g. consists of the restrictions of all distributions $w\in W^{s}_{q}(\mathbb {R}^{n})$![]() to $G$
to $G$![]() .) If (i) was not true, i.e. $s+\varepsilon =\ell +n/q-n/p$
.) If (i) was not true, i.e. $s+\varepsilon =\ell +n/q-n/p$![]() for some $\varepsilon >0$
for some $\varepsilon >0$![]() , then the Besov space $B^{s+\varepsilon }_{q,\theta }(G)$
, then the Besov space $B^{s+\varepsilon }_{q,\theta }(G)$![]() (as a part of $W^{s}_{q}(G)$
(as a part of $W^{s}_{q}(G)$![]() ) would be embedded in $W^{\ell }_{p}(G)$
) would be embedded in $W^{\ell }_{p}(G)$![]() for each $\theta \geq 1$
for each $\theta \geq 1$![]() . However, by [Reference Triebel34, p. 60, property (ii)], the last embedding is equivalent to $\theta \leq p$
. However, by [Reference Triebel34, p. 60, property (ii)], the last embedding is equivalent to $\theta \leq p$![]() . This contradiction shows that $\mathrm {(ii)}\Rightarrow \mathrm {(i)}$
. This contradiction shows that $\mathrm {(ii)}\Rightarrow \mathrm {(i)}$![]() .
.
Let $m>0$![]() , and let $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
, and let $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() . Consider an orthonormal basis $e:=(e_{j})_{j=1}^{\infty }$
. Consider an orthonormal basis $e:=(e_{j})_{j=1}^{\infty }$![]() in $L_{2}(\Gamma )$
in $L_{2}(\Gamma )$![]() formed by eigenfunctions $e_{j}\in C^{\infty }(\Gamma )$
formed by eigenfunctions $e_{j}\in C^{\infty }(\Gamma )$![]() of $A$
of $A$![]() . Let $\lambda _{j}$
. Let $\lambda _{j}$![]() denote the eigenvalue of $A$
denote the eigenvalue of $A$![]() such that $Ae_j=\lambda _{j}e_j$
such that $Ae_j=\lambda _{j}e_j$![]() . We enumerate the eigenfunctions so that $|\lambda _{j}|\leq |\lambda _{j+1}|$
. We enumerate the eigenfunctions so that $|\lambda _{j}|\leq |\lambda _{j+1}|$![]() whenever $j\geq 1$
whenever $j\geq 1$![]() . Then
. Then
where $\widetilde {c}$![]() is a certain positive number that does not depend on $j$
is a certain positive number that does not depend on $j$![]() (see e.g. [Reference Shubin32, Section 15.3]). According to theorem 4.1, the series (2.3), where $H=L_{2}(\Gamma )$
(see e.g. [Reference Shubin32, Section 15.3]). According to theorem 4.1, the series (2.3), where $H=L_{2}(\Gamma )$![]() , converges unconditionally in $W^{\ell }_{p}(\Gamma )$
, converges unconditionally in $W^{\ell }_{p}(\Gamma )$![]() on the class $W^{\ell +n/2-n/p}_{2}(\Gamma )$
on the class $W^{\ell +n/2-n/p}_{2}(\Gamma )$![]() . This class is the broadest one among the spaces $W^{s}_{q}(\Gamma )$
. This class is the broadest one among the spaces $W^{s}_{q}(\Gamma )$![]() indicated by theorem 4.1 as classes of convergence of the above series. Using the Hörmander spaces $H^{\alpha }(\Gamma )\subset W^{\ell +n/2-n/p}_{2}(\Gamma )$
indicated by theorem 4.1 as classes of convergence of the above series. Using the Hörmander spaces $H^{\alpha }(\Gamma )\subset W^{\ell +n/2-n/p}_{2}(\Gamma )$![]() as classes of the convergence, we can estimate its degree.
as classes of the convergence, we can estimate its degree.
Theorem 4.2 Let $0\leq \ell \in \mathbb {Z}$![]() , $2< p\in \mathbb {R}$
, $2< p\in \mathbb {R}$![]() and $\alpha \in \mathrm {OR}$
and $\alpha \in \mathrm {OR}$![]() . Suppose that
. Suppose that
and that the function $h$![]() decreases on $[1,\,\infty )$
decreases on $[1,\,\infty )$![]() . Then
. Then

and

for all $f\in H^{\alpha }(\Gamma )$![]() , $\lambda \geq 1$
, $\lambda \geq 1$![]() and integer-valued $k\geq 1$
and integer-valued $k\geq 1$![]() . Here, $c$
. Here, $c$![]() is a certain positive number that does not depend on $f$
is a certain positive number that does not depend on $f$![]() , $\lambda$
, $\lambda$![]() and $k$
and $k$![]() .
.
Proof. Put $\sigma :=l+n/2-n/p$![]() , $L:=(I+A^{\ast }A)$
, $L:=(I+A^{\ast }A)$![]() and $\omega (t):=t^{-\sigma /(2m)}$
and $\omega (t):=t^{-\sigma /(2m)}$![]() and $\eta (t):=h(t^{1/(2m)})$
and $\eta (t):=h(t^{1/(2m)})$![]() whenever $t\geq 1$
whenever $t\geq 1$![]() . Since $(\omega \eta )(t)=(\alpha (t^{1/(2m)}))^{-1}$
. Since $(\omega \eta )(t)=(\alpha (t^{1/(2m)}))^{-1}$![]() whenever $t\geq 1$
whenever $t\geq 1$![]() , the operator $(\omega \eta )(L)$
, the operator $(\omega \eta )(L)$![]() sets an isomorphism between $L_{2}(\Gamma )$
sets an isomorphism between $L_{2}(\Gamma )$![]() and $H^{\alpha }(\Gamma )$
and $H^{\alpha }(\Gamma )$![]() due to proposition 3.1. Hence, according to theorem 2.3 and since $h$
due to proposition 3.1. Hence, according to theorem 2.3 and since $h$![]() decreases, we have the estimates
decreases, we have the estimates

and

where $c_{0}$![]() is the norm of $\omega (L)$
is the norm of $\omega (L)$![]() considered as a bounded operator from $H=L_{2}(\Gamma )$
considered as a bounded operator from $H=L_{2}(\Gamma )$![]() to $N=W^{\ell }_{p}(\Gamma )$
to $N=W^{\ell }_{p}(\Gamma )$![]() (see the proof of theorem 4.1), $g:=((\omega \eta )(L))^{-1}f$
(see the proof of theorem 4.1), $g:=((\omega \eta )(L))^{-1}f$![]() and the number $\lambda _{j}'$
and the number $\lambda _{j}'$![]() satisfies $Le_{j}=\lambda _{j}'e_{j}$
satisfies $Le_{j}=\lambda _{j}'e_{j}$![]() , i.e. $\lambda _{j}'=1+|\lambda _{j}|^{2}$
, i.e. $\lambda _{j}'=1+|\lambda _{j}|^{2}$![]() . Hence, $\|g\|_{H}\asymp \|f\|_{H,\alpha }$
. Hence, $\|g\|_{H}\asymp \|f\|_{H,\alpha }$![]() , $\eta (1+\lambda ^{2})\asymp h(\lambda ^{1/m})$
, $\eta (1+\lambda ^{2})\asymp h(\lambda ^{1/m})$![]() as $\lambda \geq 1$
as $\lambda \geq 1$![]() , and
, and
due to $h\in \mathrm {OR}$![]() and (4.2). (As usual, the symbol $\asymp$
and (4.2). (As usual, the symbol $\asymp$![]() means the weak equivalence of positive values.) Thus, (4.5) and (4.6) imply the required estimates (4.3) and (4.4), resp.
means the weak equivalence of positive values.) Thus, (4.5) and (4.6) imply the required estimates (4.3) and (4.4), resp.
Remark 4.3 If $A$![]() is a positive definite operator in $L_{2}(\Gamma )$
is a positive definite operator in $L_{2}(\Gamma )$![]() , we have the equivalence of norms
, we have the equivalence of norms

which follows from proposition 3.1 (cf. [Reference Mikhailets and Murach28, Theorem 2.7]).
Let us consider three examples of a function $\alpha$![]() that satisfy hypotheses of theorem 4.2. As above, $0\leq \ell \in \mathbb {Z}$
that satisfy hypotheses of theorem 4.2. As above, $0\leq \ell \in \mathbb {Z}$![]() and $2< p\in \mathbb {R}$
and $2< p\in \mathbb {R}$![]() . We arbitrarily choose a number $\varepsilon >0$
. We arbitrarily choose a number $\varepsilon >0$![]() .
.
Putting $\alpha (t):=t^{l+\varepsilon +n/2-n/p}$![]() whenever $t\geq 1$
whenever $t\geq 1$![]() , we obtain the power estimates (4.3) and (4.4) with $h(\lambda ^{1/m})=\lambda ^{-\varepsilon /m}$
, we obtain the power estimates (4.3) and (4.4) with $h(\lambda ^{1/m})=\lambda ^{-\varepsilon /m}$![]() and $h(k^{1/n})=k^{-\varepsilon /n}$
and $h(k^{1/n})=k^{-\varepsilon /n}$![]() , resp. In this case, $H^{\alpha }(\Gamma )$
, resp. In this case, $H^{\alpha }(\Gamma )$![]() is a Sobolev space.
is a Sobolev space.
Taking $s:=l+n/2-n/p$![]() and $r:=s+\varepsilon$
and $r:=s+\varepsilon$![]() in (3.3) and defining $\alpha$
in (3.3) and defining $\alpha$![]() by formula (3.1) with $\beta (t)\equiv 1$
by formula (3.1) with $\beta (t)\equiv 1$![]() , we receive the Hörmander space $H^{\alpha }(\Gamma )$
, we receive the Hörmander space $H^{\alpha }(\Gamma )$![]() that is not a part of the union of all Sobolev spaces $W^{s}_{2}(\Gamma )$
that is not a part of the union of all Sobolev spaces $W^{s}_{2}(\Gamma )$![]() such that $s>\ell +n/2-n/p$
such that $s>\ell +n/2-n/p$![]() . In this case, $h(t)\searrow 0$
. In this case, $h(t)\searrow 0$![]() as $t\to \infty$
as $t\to \infty$![]() .
.
The third example is given by any function $\alpha \in \mathrm {OR}$![]() such that
such that

In this case, estimate (4.4) is of a logarithmic kind, and the space $H^{\alpha }(\Gamma )$![]() is broader than the above union of Sobolev spaces.
is broader than the above union of Sobolev spaces.
Remark 4.4 Theorems 4.1 and 4.2 remain valid for every fractional $\ell >0$![]() , which follows from their proofs.
, which follows from their proofs.
Remark 4.5 Let $0\leq \ell \in \mathbb {R}$![]() , $1\leq q<2< p$
, $1\leq q<2< p$![]() and $s=\ell +n/q-n/p$
and $s=\ell +n/q-n/p$![]() . Assertions (ii) and (iii) of theorem 4.1 hold true if we replace the normed space $W^{\ell }_{p}(\Gamma )$
. Assertions (ii) and (iii) of theorem 4.1 hold true if we replace the normed space $W^{\ell }_{p}(\Gamma )$![]() with the Triebel–Lizorkin space $F^{\ell }_{p,\theta }(\Gamma )$
with the Triebel–Lizorkin space $F^{\ell }_{p,\theta }(\Gamma )$![]() , where $1\leq \theta \leq \infty$
, where $1\leq \theta \leq \infty$![]() , or with the Besov space $B^{\ell }_{p,\theta }(\Gamma )$
, or with the Besov space $B^{\ell }_{p,\theta }(\Gamma )$![]() , where $2\leq \theta \leq \infty$
, where $2\leq \theta \leq \infty$![]() , and replace the convergence class $W^{s}_{q}(\Gamma )$
, and replace the convergence class $W^{s}_{q}(\Gamma )$![]() with $F^{s}_{q,\eta }(\Gamma )$
with $F^{s}_{q,\eta }(\Gamma )$![]() , where $1\leq \eta \leq \infty$
, where $1\leq \eta \leq \infty$![]() , or with $B^{s}_{q,\eta }(\Gamma )$
, or with $B^{s}_{q,\eta }(\Gamma )$![]() , where $1\leq \eta \leq 2$
, where $1\leq \eta \leq 2$![]() . This follows from the continuous embeddings
. This follows from the continuous embeddings
and
[Reference Triebel34, p. 60, properties (ii) and (iii)], as we can conclude analysing the proof of this theorem. Of course, it is natural to restrict ourselves to the marginal cases where $\eta =\infty$![]() and $\theta =1$
and $\theta =1$![]() for $F$
for $F$![]() -spaces and where $\eta =\theta =2$
-spaces and where $\eta =\theta =2$![]() for $B$
for $B$![]() -spaces. In these cases we obtain narrower normed spaces than $W^{\ell }_{p}(\Gamma )$
-spaces. In these cases we obtain narrower normed spaces than $W^{\ell }_{p}(\Gamma )$![]() and get broader convergence classes than $W^{s}_{q}(\Gamma )$
and get broader convergence classes than $W^{s}_{q}(\Gamma )$![]() . Of course, theorem 4.2 is also valid under this replacement of $W^{\ell }_{p}(\Gamma )$
. Of course, theorem 4.2 is also valid under this replacement of $W^{\ell }_{p}(\Gamma )$![]() .
.
5. Uniform convergence
We use this term to refer to the convergence in the normed space $C^{\ell }(\Gamma )$![]() of $\ell$
of $\ell$![]() times continuously differentiable functions on the manifold $\Gamma$
times continuously differentiable functions on the manifold $\Gamma$![]() , with $0\leq \ell \in \mathbb {Z}$
, with $0\leq \ell \in \mathbb {Z}$![]() . Specifically, if $\ell =0$
. Specifically, if $\ell =0$![]() , we get the convergence in the space $C(\Gamma )$
, we get the convergence in the space $C(\Gamma )$![]() of continuous functions on $\Gamma$
of continuous functions on $\Gamma$![]() , i.e. the uniform convergence on $\Gamma$
, i.e. the uniform convergence on $\Gamma$![]() . Let $\|\cdot \|_{C,\ell }$
. Let $\|\cdot \|_{C,\ell }$![]() denote the norm in $C^{\ell }(\Gamma )$
denote the norm in $C^{\ell }(\Gamma )$![]() . If $\ell \geq 1$
. If $\ell \geq 1$![]() , we use the norm
, we use the norm

with $\pi _{j}$![]() and $\chi _{j}$
and $\chi _{j}$![]() being taking from the definition of Hörmander spaces over $\Gamma$
being taking from the definition of Hörmander spaces over $\Gamma$![]() . Here, of course, $\varrho =(\varrho _1,\,\ldots,\,\varrho _n)$
. Here, of course, $\varrho =(\varrho _1,\,\ldots,\,\varrho _n)$![]() is a multi-index, $|\varrho |=\varrho _1+\cdots +\varrho _n$
is a multi-index, $|\varrho |=\varrho _1+\cdots +\varrho _n$![]() , and $\partial ^{\varrho }$
, and $\partial ^{\varrho }$![]() is the partial derivative corresponding to $\varrho$
is the partial derivative corresponding to $\varrho$![]() .
.
Theorem 5.1 Suppose that $0< m\in \mathbb {R}$![]() , $0\leq \ell \in \mathbb {Z}$
, $0\leq \ell \in \mathbb {Z}$![]() and $\alpha \in \mathrm {OR}$
and $\alpha \in \mathrm {OR}$![]() . Then the following three conditions are equivalent:
. Then the following three conditions are equivalent:
(i)
\[ \int\limits_{1}^{\infty}\frac{t^{2\ell+n-1}}{\alpha^{2}(t)}\,{\rm d}t<\infty; \]
(ii) there exists a PsDO $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
 that spectral decomposition (4.1) induced by $A$
that spectral decomposition (4.1) induced by $A$ converges in $C^{\ell }(\Gamma )$
converges in $C^{\ell }(\Gamma )$ on the class $H^{\alpha }(\Gamma )$
on the class $H^{\alpha }(\Gamma )$ ;
;(iii) the expansions in eigenfunctions of an arbitrary PsDO from $\mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
 converge unconditionally in $C^{\ell }(\Gamma )$
converge unconditionally in $C^{\ell }(\Gamma )$ on the class $H^{\alpha }(\Gamma )$
on the class $H^{\alpha }(\Gamma )$ .
.
Proof. It follows from Hörmander's embedding theorem [Reference Hörmander17, Theorem 2.2.7] that
as is seen from [Reference Mikhailets and Murach28, Proposition 2.6 (vi)].
Let us now prove that $\mathrm {(i)}\Rightarrow \mathrm {(iii)}$![]() . We assume (i) to hold true and arbitrarily choose a PsDO $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
. We assume (i) to hold true and arbitrarily choose a PsDO $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() . Owing to (5.1), the space $H^{\alpha }(\Gamma )$
. Owing to (5.1), the space $H^{\alpha }(\Gamma )$![]() lies in $L_{2}(\Gamma )$
lies in $L_{2}(\Gamma )$![]() . Hence, the function $1/\alpha$
. Hence, the function $1/\alpha$![]() is bounded on $[1,\,\infty )$
is bounded on $[1,\,\infty )$![]() in view of [Reference Hörmander17, Theorem 2.2.2]. We put $\omega (t):=1/\alpha (t^{1/(2m)})$
in view of [Reference Hörmander17, Theorem 2.2.2]. We put $\omega (t):=1/\alpha (t^{1/(2m)})$![]() whenever $t\geq 1$
whenever $t\geq 1$![]() and consider the function $\omega (L)$
and consider the function $\omega (L)$![]() of the operator $L=(I+A^{\ast }A)\in \mathrm {NE}\Psi _{\mathrm {ph}}^{2m}(\Gamma )$
of the operator $L=(I+A^{\ast }A)\in \mathrm {NE}\Psi _{\mathrm {ph}}^{2m}(\Gamma )$![]() acting in $L_{2}(\Gamma )$
acting in $L_{2}(\Gamma )$![]() . According to proposition 3.1, the operator $\omega (L)$
. According to proposition 3.1, the operator $\omega (L)$![]() sets an isomorphism between $L_{2}(\Gamma )$
sets an isomorphism between $L_{2}(\Gamma )$![]() and $H^{\alpha }(\Gamma )$
and $H^{\alpha }(\Gamma )$![]() . Hence, owing to (5.1), this operator acts continuously from $H=L_{2}(\Gamma )$
. Hence, owing to (5.1), this operator acts continuously from $H=L_{2}(\Gamma )$![]() to $N:=C^{\ell }(\Gamma )$
to $N:=C^{\ell }(\Gamma )$![]() , as noticed in remark 2.4. We therefore conclude by theorem 2.3, where $\eta (t)\equiv 1$
, as noticed in remark 2.4. We therefore conclude by theorem 2.3, where $\eta (t)\equiv 1$![]() , that the expansions in eigenfunctions of $L$
, that the expansions in eigenfunctions of $L$![]() converge unconditionally in $C^{\ell }(\Gamma )$
converge unconditionally in $C^{\ell }(\Gamma )$![]() on the class $H^{\alpha }(\Gamma )$
on the class $H^{\alpha }(\Gamma )$![]() . We have proved that $\mathrm {(i)}\Rightarrow \mathrm {(iii)}$
. We have proved that $\mathrm {(i)}\Rightarrow \mathrm {(iii)}$![]() .
.
The implication $\mathrm {(iii)}\Rightarrow \mathrm {(ii)}$![]() is obvious.
is obvious.
The implication $\mathrm {(ii)}\Rightarrow \mathrm {(i)}$![]() is true because assertion (ii) entails the inclusion $H^{\alpha }(\Gamma )\subset C^{\ell }(\Gamma )$
is true because assertion (ii) entails the inclusion $H^{\alpha }(\Gamma )\subset C^{\ell }(\Gamma )$![]() and hence implies (i) by (5.1).
and hence implies (i) by (5.1).
Let $m>0$![]() and $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$
and $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() . As in the previous section, $e:=(e_{j})_{j=1}^{\infty }$
. As in the previous section, $e:=(e_{j})_{j=1}^{\infty }$![]() is an orthonormal basis in $H=L_{2}(\Gamma )$
is an orthonormal basis in $H=L_{2}(\Gamma )$![]() formed by eigenfunctions $e_{j}$
formed by eigenfunctions $e_{j}$![]() of $A$
of $A$![]() , with $Ae_j=\lambda _{j}e_j$
, with $Ae_j=\lambda _{j}e_j$![]() and $|\lambda _{j}|\leq |\lambda _{j+1}|$
and $|\lambda _{j}|\leq |\lambda _{j+1}|$![]() whenever $j\geq 1$
whenever $j\geq 1$![]() . We complement theorem 5.1 by estimating the degree of the uniform convergence of series (2.3) on Hörmander classes.
. We complement theorem 5.1 by estimating the degree of the uniform convergence of series (2.3) on Hörmander classes.
Theorem 5.2 Let $0\leq \ell \in \mathbb {Z}$![]() , and suppose that certain functions $h,\,\beta \in \mathrm {OR}$
, and suppose that certain functions $h,\,\beta \in \mathrm {OR}$![]() satisfy the following conditions: $h(t)\to 0$
satisfy the following conditions: $h(t)\to 0$![]() as $t\to \infty$
as $t\to \infty$![]() , $h$
, $h$![]() decreases on $[1,\,\infty )$
decreases on $[1,\,\infty )$![]() , and
, and

Put $\alpha :=\beta /h$![]() , and note that the function $\alpha$
, and note that the function $\alpha$![]() belongs to $\mathrm {OR}$
belongs to $\mathrm {OR}$![]() and satisfies hypothesis (i) of theorem 5.1. Then
and satisfies hypothesis (i) of theorem 5.1. Then

and

for all $f\in H^{\alpha }(\Gamma )$![]() , $\lambda \geq 1$
, $\lambda \geq 1$![]() , and integer-valued $k\geq 1$
, and integer-valued $k\geq 1$![]() . Here, $c$
. Here, $c$![]() is a certain positive number that does not depend on $f$
is a certain positive number that does not depend on $f$![]() , $\lambda$
, $\lambda$![]() and $k$
and $k$![]() .
.
Proof. Let, as above, $L:=(I+A^{\ast }A)$![]() , and consider the bounded functions $\omega (t):=(\beta (t^{1/(2m)}))^{-1}$
, and consider the bounded functions $\omega (t):=(\beta (t^{1/(2m)}))^{-1}$![]() and $\eta (t):=h(t^{1/(2m)})$
and $\eta (t):=h(t^{1/(2m)})$![]() of $t\geq 1$
of $t\geq 1$![]() . (As to $\omega$
. (As to $\omega$![]() note that every function of class $\mathrm {OR}\cap L_{1}[1,\,\infty )$
note that every function of class $\mathrm {OR}\cap L_{1}[1,\,\infty )$![]() is bounded on $[1,\,\infty )$
is bounded on $[1,\,\infty )$![]() ). Since $(\omega \eta )(t)\equiv (\alpha (t^{1/(2m)}))^{-1}$
). Since $(\omega \eta )(t)\equiv (\alpha (t^{1/(2m)}))^{-1}$![]() , the operator $(\omega \eta )(L)$
, the operator $(\omega \eta )(L)$![]() sets an isomorphism between $H=L_{2}(\Gamma )$
sets an isomorphism between $H=L_{2}(\Gamma )$![]() and $H^{\alpha }(\Gamma )$
and $H^{\alpha }(\Gamma )$![]() due to [Reference Mikhailets and Murach28, Theorem 2.23]. Hence, according to theorem 2.3 and since the function $h$
due to [Reference Mikhailets and Murach28, Theorem 2.23]. Hence, according to theorem 2.3 and since the function $h$![]() decreases, we obtain the estimates of form (4.5) and (4.6), with the norm $\|\cdot \|_{C,\ell }$
decreases, we obtain the estimates of form (4.5) and (4.6), with the norm $\|\cdot \|_{C,\ell }$![]() being instead of $\|\cdot \|_{W,\ell,p}$
being instead of $\|\cdot \|_{W,\ell,p}$![]() . These estimates imply (5.2) and (5.3) with the help of the same reasoning as that given in the proof of theorem 4.2.
. These estimates imply (5.2) and (5.3) with the help of the same reasoning as that given in the proof of theorem 4.2.
Let us indicate important examples of the function $\alpha$![]() satisfying hypotheses of theorem 5.2. We let $0\leq \ell \in \mathbb {Z}$
satisfying hypotheses of theorem 5.2. We let $0\leq \ell \in \mathbb {Z}$![]() and arbitrarily choose numbers $\varepsilon$
and arbitrarily choose numbers $\varepsilon$![]() and $\delta$
and $\delta$![]() such that $0<\delta <\varepsilon$
such that $0<\delta <\varepsilon$![]() .
.
Putting $\alpha (t):=t^{l+n/2+\varepsilon +\delta }$![]() whenever $t\geq 1$
whenever $t\geq 1$![]() , we obtain power estimates (5.2) and (5.3) with $h(t)\equiv t^{-\delta }$
, we obtain power estimates (5.2) and (5.3) with $h(t)\equiv t^{-\delta }$![]() . Such power estimates hold true for functions
. Such power estimates hold true for functions
To achieve the limiting value $s=l+n/2$![]() , we put $\alpha (t):=t^{l+n/2}\log ^{1/2+\varepsilon +\delta }(t+1)$
, we put $\alpha (t):=t^{l+n/2}\log ^{1/2+\varepsilon +\delta }(t+1)$![]() whenever $t\geq 1$
whenever $t\geq 1$![]() and receive the estimates of a logarithmic kind with ${h(t)\equiv \log ^{-\delta }(t+1)}$
and receive the estimates of a logarithmic kind with ${h(t)\equiv \log ^{-\delta }(t+1)}$![]() .
.
6. Applications to ordinary differential operators
Let us discuss results of § 4 and 5 in the case where $\Gamma$![]() is a circle $\mathbb {T}$
is a circle $\mathbb {T}$![]() of the unit radius and when $A$
of the unit radius and when $A$![]() is an (ordinary) differential operator on $\mathbb {T}$
is an (ordinary) differential operator on $\mathbb {T}$![]() of order $m$
of order $m$![]() with infinitely smooth complex-valued coefficients. Let $\tau$
with infinitely smooth complex-valued coefficients. Let $\tau$![]() , with $0\leq \tau \leq 2\pi$
, with $0\leq \tau \leq 2\pi$![]() , set a natural parametrization of $\mathbb {T}$
, set a natural parametrization of $\mathbb {T}$![]() . We suppose that the leading coefficient of $A$
. We suppose that the leading coefficient of $A$![]() does not equal zero for any $\tau$
does not equal zero for any $\tau$![]() , which is equivalent to the ellipticity of $A$
, which is equivalent to the ellipticity of $A$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() . We also assume that $A$
. We also assume that $A$![]() is a normal operator in the Hilbert space $H:=L_{2}(\mathbb {T})$
is a normal operator in the Hilbert space $H:=L_{2}(\mathbb {T})$![]() . If all coefficients of $A$
. If all coefficients of $A$![]() are constant, this assumption holds true. In the case of variables coefficients, we recall the following necessary and sufficient condition for $A$
are constant, this assumption holds true. In the case of variables coefficients, we recall the following necessary and sufficient condition for $A$![]() to be self-adjoint in $L_{2}(\mathbb {T})$
to be self-adjoint in $L_{2}(\mathbb {T})$![]() [Reference Naimark31, Chapter I, Section 1, Subsection 5]: $A$
[Reference Naimark31, Chapter I, Section 1, Subsection 5]: $A$![]() is a sum of differential operators of the form
is a sum of differential operators of the form
provided that $\mu _{k}$![]() and $\nu _{k}$
and $\nu _{k}$![]() are real-valued functions of class $C^{\infty }(\mathbb {T})$
are real-valued functions of class $C^{\infty }(\mathbb {T})$![]() . Specifically, if all coefficients of $A$
. Specifically, if all coefficients of $A$![]() are real-valued, the above condition means that $m$
are real-valued, the above condition means that $m$![]() is even and that $A$
is even and that $A$![]() is the sum of $A_{2k}$
is the sum of $A_{2k}$![]() with $k=0,\,1,\,\ldots,\,m/2$
with $k=0,\,1,\,\ldots,\,m/2$![]() .
.
Let $e:=(e_{j})_{j=1}^{\infty }$![]() be an orthonormal basis in $H=L_{2}(\mathbb {T})$
be an orthonormal basis in $H=L_{2}(\mathbb {T})$![]() formed by eigenfunctions $e_{j}$
formed by eigenfunctions $e_{j}$![]() of $A$
of $A$![]() , with $Ae_j=\lambda _{j}e_j$
, with $Ae_j=\lambda _{j}e_j$![]() and $|\lambda _{j}|\leq |\lambda _{j+1}|$
and $|\lambda _{j}|\leq |\lambda _{j+1}|$![]() whenever $j\geq 1$
whenever $j\geq 1$![]() . Given a function $f\in L_{2}(\mathbb {T})$
. Given a function $f\in L_{2}(\mathbb {T})$![]() , we consider its expansion
, we consider its expansion

in these eigenfunctions, the expansion converging in $L_{2}(\mathbb {T})$![]() . Let $0\leq \ell \in \mathbb {Z}$
. Let $0\leq \ell \in \mathbb {Z}$![]() and $2< p\in \mathbb {R}$
and $2< p\in \mathbb {R}$![]() . If $1< q\leq 2$
. If $1< q\leq 2$![]() and $s\geq \ell +1/q-1/p$
and $s\geq \ell +1/q-1/p$![]() , then theorem 4.1 implies that, for every $f\in W^{s}_{q}(\mathbb {T})$
, then theorem 4.1 implies that, for every $f\in W^{s}_{q}(\mathbb {T})$![]() , this expansion converges in the $p$
, this expansion converges in the $p$![]() -th mean unconditionally and preserves this convergence after the termwise differentiation up to $\ell$
-th mean unconditionally and preserves this convergence after the termwise differentiation up to $\ell$![]() times. If a function parameter $\alpha \in \mathrm {OR}$
times. If a function parameter $\alpha \in \mathrm {OR}$![]() satisfies
satisfies

then theorem 5.1 implies that, for every $f\in H^{\alpha }(\mathbb {T})$![]() , the expansion converges uniformly and unconditionally and preserve this convergence after the same differentiation. Note that the derivatives of $e_j(\tau )$
, the expansion converges uniformly and unconditionally and preserve this convergence after the same differentiation. Note that the derivatives of $e_j(\tau )$![]() may not form an orthogonal basis in $L_{2}(\mathbb {T})$
may not form an orthogonal basis in $L_{2}(\mathbb {T})$![]() . Assuming $\alpha$
. Assuming $\alpha$![]() to satisfy the hypotheses of theorem 4.2 or 5.2, we see that estimates (4.3) and (5.2) become
to satisfy the hypotheses of theorem 4.2 or 5.2, we see that estimates (4.3) and (5.2) become

and

whenever $f\in H^{\alpha }(\mathbb {T})$![]() and $\lambda \geq 1$
and $\lambda \geq 1$![]() ; here, $h(\lambda ^{1/m})\to 0$
; here, $h(\lambda ^{1/m})\to 0$![]() as $\lambda \to \infty$
as $\lambda \to \infty$![]() . Formulas (4.4) and (5.3) are rewritten quite similarly.
. Formulas (4.4) and (5.3) are rewritten quite similarly.
Considering remark 4.3 in the $A:=1-d^{2}/d^{2}\tau$![]() case, we conclude that the norm $\|f\|_{H,\alpha }$
case, we conclude that the norm $\|f\|_{H,\alpha }$![]() in the space $H^{\alpha }(\mathbb {T})$
in the space $H^{\alpha }(\mathbb {T})$![]() is equivalent to the norm
is equivalent to the norm

with $c_{j}(f)$![]() being the Fourier coefficient of $f$
being the Fourier coefficient of $f$![]() with respect to the eigenfunction $e_{j}(\tau ):=(2\pi )^{-1}e^{ij\tau }$
with respect to the eigenfunction $e_{j}(\tau ):=(2\pi )^{-1}e^{ij\tau }$![]() of the differential operator ${1-d^{2}/d^{2}\tau }$
of the differential operator ${1-d^{2}/d^{2}\tau }$![]() .
.
In this case or if $A=d/d\tau$![]() , expansion (6.1) becomes the Fourier series with respect to the complex trigonometric system on $[0,\,2\pi ]$
, expansion (6.1) becomes the Fourier series with respect to the complex trigonometric system on $[0,\,2\pi ]$![]() . The above results on the mean convergence are new even for this series.
. The above results on the mean convergence are new even for this series.
Ending this section, we remark that theorems 4.1, 4.2, 5.1 and 5.2 remain valid in the case where the coefficients of the ordinary differential operator $A$![]() have finite smoothness depending, of course, on the parameters involved in these theorems. We will not specify the smoothness.
have finite smoothness depending, of course, on the parameters involved in these theorems. We will not specify the smoothness.
7. Applications to multiple Fourier series
Let $2\leq n\in \mathbb {Z}$![]() , and consider the $n$
, and consider the $n$![]() -dimensional torus $\mathbb {T}^{n}$
-dimensional torus $\mathbb {T}^{n}$![]() ; as above, $\mathbb {T}$
; as above, $\mathbb {T}$![]() is a circle of the unit radius. Let $A$
is a circle of the unit radius. Let $A$![]() denote the Laplace–Beltrami operator on $\mathbb {T}^{n}$
denote the Laplace–Beltrami operator on $\mathbb {T}^{n}$![]() . It belongs to $\mathrm {NE}\Psi _{\mathrm {ph}}^{2}(\Gamma )$
. It belongs to $\mathrm {NE}\Psi _{\mathrm {ph}}^{2}(\Gamma )$![]() , is a self-adjoint operator in the Hilbert space $H:=L_{2}(\mathbb {T}^{n})$
, is a self-adjoint operator in the Hilbert space $H:=L_{2}(\mathbb {T}^{n})$![]() and takes the form $A=\partial ^{2}/\partial ^{2}\tau _{1}+\cdots + \partial ^{2}/\partial ^{2}\tau _{n}$
and takes the form $A=\partial ^{2}/\partial ^{2}\tau _{1}+\cdots + \partial ^{2}/\partial ^{2}\tau _{n}$![]() , where $\tau _{k}$
, where $\tau _{k}$![]() , with $0\leq \tau _{k}\leq 2\pi$
, with $0\leq \tau _{k}\leq 2\pi$![]() , sets a natural parametrization of the $k$
, sets a natural parametrization of the $k$![]() -th specimen of $\mathbb {T}$
-th specimen of $\mathbb {T}$![]() . The eigenfunctions $e_{j}(\tau ):=(2\pi )^{-n}e^{i(j_1\tau _1+\cdots +j_n\tau _n)}$
. The eigenfunctions $e_{j}(\tau ):=(2\pi )^{-n}e^{i(j_1\tau _1+\cdots +j_n\tau _n)}$![]() of $A$
of $A$![]() , where $\tau =(\tau _1,\,\ldots,\,\tau _n)\in [0,\,2\pi ]^{n}$
, where $\tau =(\tau _1,\,\ldots,\,\tau _n)\in [0,\,2\pi ]^{n}$![]() and $j=(j_1,\,\ldots,\,j_n)\in \mathbb {Z}^{n}$
and $j=(j_1,\,\ldots,\,j_n)\in \mathbb {Z}^{n}$![]() , form an orthonormal basis in the Hilbert space $L_{2}(\mathbb {T}^{n})$
, form an orthonormal basis in the Hilbert space $L_{2}(\mathbb {T}^{n})$![]() . Given a function $f\in L_{2}(\mathbb {T}^{n})$
. Given a function $f\in L_{2}(\mathbb {T}^{n})$![]() , we consider its expansion in the multiple Fourier series
, we consider its expansion in the multiple Fourier series
the expansion converging in $L_{2}(\mathbb {T}^{n})$![]() . Here, $c_j(f)$
. Here, $c_j(f)$![]() denotes the Fourier coefficient of $f$
denotes the Fourier coefficient of $f$![]() with respect to $e_{j}$
with respect to $e_{j}$![]() ,
,
Since the termwise differentiation of series (7.1) gives the multiple Fourier series again, we restrict ourselves to the $\ell =0$![]() case applying results of § 4 and 5 to expansion (7.1). Let $2< p<\infty$
case applying results of § 4 and 5 to expansion (7.1). Let $2< p<\infty$![]() . If $1< q\leq 2$
. If $1< q\leq 2$![]() and $s\geq n/q-n/p$
and $s\geq n/q-n/p$![]() , it follows from theorem 4.1 that, whatever $f\in W^{s}_{q}(\mathbb {T}^{n})$
, it follows from theorem 4.1 that, whatever $f\in W^{s}_{q}(\mathbb {T}^{n})$![]() , expansion (7.1) is unconditionally convergent in the $p$
, expansion (7.1) is unconditionally convergent in the $p$![]() -th mean. If a function parameter $\alpha \in \mathrm {OR}$
-th mean. If a function parameter $\alpha \in \mathrm {OR}$![]() satisfies
satisfies

it follows from theorem 5.1 that, for every $f\in H^{\alpha }(\mathbb {T}^{n})$![]() , this expansion converges unconditionally uniformly (on $\mathbb {T}^{n}$
, this expansion converges unconditionally uniformly (on $\mathbb {T}^{n}$![]() ). Considering the last result in the case of power functions $\alpha (t)\equiv t^{s}$
). Considering the last result in the case of power functions $\alpha (t)\equiv t^{s}$![]() , we conclude that expansion (7.1) converges unconditionally uniformly on each class $W^{s}_{2}(\mathbb {T}^{n})$
, we conclude that expansion (7.1) converges unconditionally uniformly on each class $W^{s}_{2}(\mathbb {T}^{n})$![]() where $s>n/2$
where $s>n/2$![]() . If $n$
. If $n$![]() is odd, such a conclusion is substantiated in [Reference Ilin20, Theorem A.1] concerning the uniform convergence over the torus.
is odd, such a conclusion is substantiated in [Reference Ilin20, Theorem A.1] concerning the uniform convergence over the torus.
Assuming $\alpha$![]() to satisfy hypotheses of theorem 4.2 or 5.2, we rewrite estimates (4.3) and (5.2) as follows:
to satisfy hypotheses of theorem 4.2 or 5.2, we rewrite estimates (4.3) and (5.2) as follows:

and

whenever $f\in H^{\alpha }(\mathbb {T})$![]() and $\lambda \geq 1$
and $\lambda \geq 1$![]() . Here, $h(\lambda )\to 0$
. Here, $h(\lambda )\to 0$![]() as $\lambda \to \infty$
as $\lambda \to \infty$![]() , and we take into account that $Ae_{j}=-\|j\|^{2}e_{j}$
, and we take into account that $Ae_{j}=-\|j\|^{2}e_{j}$![]() , with $\|j\|:=(j_{1}^{2}+\cdots +j_{n}^{2})^{1/2}$
, with $\|j\|:=(j_{1}^{2}+\cdots +j_{n}^{2})^{1/2}$![]() . According to remark 4.3, the norm $\|f\|_{H,\alpha }$
. According to remark 4.3, the norm $\|f\|_{H,\alpha }$![]() in $H^{\alpha }(\mathbb {T}^{n})$
in $H^{\alpha }(\mathbb {T}^{n})$![]() is equivalent to the norm
is equivalent to the norm

If $\alpha$![]() belongs to $\mathrm {OR}$
belongs to $\mathrm {OR}$![]() and satisfies (7.2), then
and satisfies (7.2), then
for every $f\in H^{\alpha }(\mathbb {T}^{n})$![]() , which means the absolute convergence of the Fourier series (7.1) of $f$
, which means the absolute convergence of the Fourier series (7.1) of $f$![]() and follows from the unconditional uniform convergence of this series. As is known [Reference Alimov, Il'in and Nikishin2, Section 6, Subsection 3], property (7.3) is fulfilled provided that $f$
and follows from the unconditional uniform convergence of this series. As is known [Reference Alimov, Il'in and Nikishin2, Section 6, Subsection 3], property (7.3) is fulfilled provided that $f$![]() belongs to the Hölder space $\mathcal {C}^{\ell }(\mathbb {T}^{n})$
belongs to the Hölder space $\mathcal {C}^{\ell }(\mathbb {T}^{n})$![]() for some $\ell >n/2$
for some $\ell >n/2$![]() and is not fulfilled for certain functions $f\in \mathcal {C}^{n/2}(\mathbb {T}^{n})$
and is not fulfilled for certain functions $f\in \mathcal {C}^{n/2}(\mathbb {T}^{n})$![]() . Our sufficient condition for (7.3) to hold true is weaker than that indicated in terms of Hölder spaces. This is demonstrated by the example when $\alpha (t)\equiv t^{n/2}\log ^{1/2+\varepsilon }(t+1)$
. Our sufficient condition for (7.3) to hold true is weaker than that indicated in terms of Hölder spaces. This is demonstrated by the example when $\alpha (t)\equiv t^{n/2}\log ^{1/2+\varepsilon }(t+1)$![]() for some $\varepsilon >0$
for some $\varepsilon >0$![]() , which gives the broader space $H^{\alpha }(\mathbb {T}^{n})$
, which gives the broader space $H^{\alpha }(\mathbb {T}^{n})$![]() (satisfying (7.2)) than the union of all $\mathcal {C}^{\ell }(\mathbb {T}^{n})$
(satisfying (7.2)) than the union of all $\mathcal {C}^{\ell }(\mathbb {T}^{n})$![]() with $\ell >n/2$
with $\ell >n/2$![]() .
.
Note that of considerable interest is also the study of conditions for multiple Fourier series to converge almost everywhere. Relevant results are expounded in [Reference Alimov, Il'in and Nikishin2, Reference Alimov, Il'in and Nikishin3, Reference Ashurov6, Reference Carbery and Soria11, Reference Golubov16] and references therein.
8. Concluding remarks
Remark 8.1 Our results are also applied to the case where the operator $A\in \mathrm {NE}\Psi _{\mathrm {ph}}^{m}(\Gamma )$![]() is of negative order $m$
is of negative order $m$![]() because the resolvent of $A$
because the resolvent of $A$![]() belongs to $\mathrm {NE}\Psi _{\mathrm {ph}}^{-m}(\Gamma )$
belongs to $\mathrm {NE}\Psi _{\mathrm {ph}}^{-m}(\Gamma )$![]() , is of positive order and has the same eigenfunctions as $A$
, is of positive order and has the same eigenfunctions as $A$![]() does.
does.
Remark 8.2 According to theorem 2.3, the left-hand side of (2.4) (i.e. the norm of a remainder of series (2.1)) depends monotonically on the corresponding set of eigenvectors of $L$![]() . Hence, the estimates in theorems 4.2 and 5.2 remain true if the written sums additionally contain some other terms of the eigenfunction expansion. Specifically, estimates (4.3) and (5.2) are valid if we replace the sum
. Hence, the estimates in theorems 4.2 and 5.2 remain true if the written sums additionally contain some other terms of the eigenfunction expansion. Specifically, estimates (4.3) and (5.2) are valid if we replace the sum
with any partial sum of the series in the arbitrarily numbered eigenfunctions $e_{j}$![]() provided that the later sum contains all $e_{j}$
provided that the later sum contains all $e_{j}$![]() subject to $|\lambda _{j}|\leq \lambda$
subject to $|\lambda _{j}|\leq \lambda$![]() .
.
Remark 8.3 If the closed manifold $\Gamma$![]() is a sphere (of any dimension), the results of § 4 and 5 admit further detailing and are also new.
is a sphere (of any dimension), the results of § 4 and 5 admit further detailing and are also new.
Remark 8.4 Our approach allows other applications, specifically, to elliptic matrix pseudodifferential operators and elliptic differential operators in a bounded Euclidean domain.
Acknowledgements
This work was funded by the Czech Academy of Sciences within grant RVO:67985840 and by the National Academy of Sciences of Ukraine. The authors were supported by the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 873071 (SOMPATY: Spectral Optimization: From Mathematics to Physics and Advanced Technology). The second named author was also supported by a grant from the Simons Foundation (1030291, A.A.M.).