Fifty years ago Marcinkiewicz and Zygmund studied the circular structure of the limit points of the partial sums for (C, 1) summable Taylor series. More specifically, let
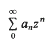
be a power series with complex coefficients, let
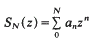
be the partial sums, and let
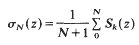
be the Cesàro averages. When the sequence σn(z) converges to a finite limit σ(Z), we say that the Taylor series is (C, 1) summable and σ(z) is the (C, 1) sum of the series. Concerning (C, 1) summable Taylor series Marcinkiewicz and Zygmund ([5], [6] Vol. II, p. 178) established the following theorem.