Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T18:36:18.444Z Has data issue: false hasContentIssue false
  • English
  • Français

On pairs of cubic Diophantine inequalities

Part of: Diophantine equations

Published online by Cambridge University Press:  26 February 2010

J. Brüdern  and
R. J. Cook
J. Brüdern
Affiliation:
Mathematisches Institut, Bunsenstrasse 3-5, 3400 Göttingen, Germany.
R. J. Cook
Affiliation:
Dept. of Pure Mathematics, University of Sheffield Hicks Building, Sheffield S3 7RH, U.K..
Get access

Extract

The problem of finding rational points on varieties defined by two additive cubic equations has attracted some interest. Davenport and Lewis [12], Cook [8] and Vaughan [16] showed that the pair of equations

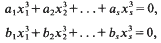
with integer coefficients a,, bt always has a nontrivial solution when s = 18, s = 17, and 5 = 16 respectively. Vaughan's result in s = 16 variables is best possible since there are examples of pairs of equations (1) with s = 15 which fail to vanish simultaneously in the 7-adic field. However if the existence of a 7-adic solution is assured then Baker and Briidern [2], building on work of Cook [9], showed that s = 16 could be replaced by s = 15, and recently Briidern [5] has obtained the result with s = 14.

MSC classification

Secondary: 11D75: Diophantine inequalities
Type
Research Article
Information
Mathematika , Volume 38 , Issue 2 , December 1991 , pp. 250 - 263
Copyright
Copyright © University College London 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, R. C.. Diagonal cubic equations III. Proc. London Math. Soc, (3), 58 (1989), 495–518.CrossRefGoogle Scholar
2.Baker, R. C. and BrÜdern, J.. On pairs of additive cubic equations. J. reine angew. Math., 391 (1988), 157–180.Google Scholar
3.BrÜidern, J.. Additive diophantine inequalities with mixed powers I. Mathematika, 34 (1987), 124–130.CrossRefGoogle Scholar
4.BrÜdern, J.. Cubic diophantine inequalities. Mathematika, 35 (1989), 51–58.CrossRefGoogle Scholar
5.BrÜidern, J.. Pairs of diagonal cubic forms. Proc. London Math. Soc, (3), 61 (1990), 273–343.CrossRefGoogle Scholar
6.de Bruijn, N. G.. The asymptotic behaviour of a function occurring in the theory of primes. J. Indian Math. Soc. (N.S.), 15 (1951), 25–52.Google Scholar
7.Cook, R. J.. Simultaneous quadratic inequalities. Acta Arith., 25 (1974), 337–346.CrossRefGoogle Scholar
8.Cook, R. J.. Pairs of additive equations. Michigan Math. J., 19 (1972), 325–333.CrossRefGoogle Scholar
9.Cook, R. J.. Pairs of additive congruences: cubic congruences. Mathematika, 32 (1985), 286–300.CrossRefGoogle Scholar
10.Davenport, H.. On indefinite quadratic forms in many variables. Mathematika, 3 (1956), 81–101.CrossRefGoogle Scholar
11.Davenport, H.. Cubic forms in thirty-two variables. Phil. Trans. Royal Soc, A, 251 (1959), 193–232.Google Scholar
12.Davenport, H. and Lewis, D. J.. Cubic equations of additive type. Phil. Trans. Royal Soc. Ser. A., 261 (1966), 97–136.Google Scholar
13.Margulis, G. A.. Formes quadratiques indefinie et flots unipotents sur les espaces homogenes. C. R. Acad. Set, Paris, Ser. J, 304 (1987), 249–253.Google Scholar
14.Pitman, J.. Pairs of diagonal inequalities. Recent Progress in Analytic Number Theory, vol. 2, Halberstam, H., Hooley, C., eds. (Academic Press, London, 1981).Google Scholar
15.Schmidt, W. M.. Linear forms with algebraic coefficients. J. Number Theory, 3 (1971), 253–277.CrossRefGoogle Scholar
16.Vaughan, R. C.. On pairs of additive cubic equations. Proc. London Math. Soc. (3), 34 (1977), 354–364.CrossRefGoogle Scholar
17.Vaughan, R. C.. The Hardy-Littlewood Method (University Press, Cambridge, 1981).Google Scholar
18.Vaughan, R. C.. On Waring's problem for cubes. J. reine angew. Math., 365 (1986), 122–170.Google Scholar
19.Vaughan, R. C.. A new iterative method in Waring's problem. Acta Math., 162 (1989), 1–71.CrossRefGoogle Scholar