Article contents
Prolongations of valuations to simple transcendental extensions with given residue field and value group
Published online by Cambridge University Press: 26 February 2010
Abstract
Let K0(x) be a simple transcendental extension of a field K0, υ0 be a valuation of K0 with value group G0 and residue field K0. Suppose 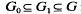 is an inclusion of totally ordered abelian groups with [G1: G0] < ∞ such that G is the direct sum of G1 and an infinite cyclic group. It is proved that there exists an (explicitly constructible) valuation υ of K0(x) extending υ0 such that the value group of υ is G and its residue field is k, where k is a given finite extension of k0. This is analogous to a result of Matignon and Ohm [2, Corollary 3.2] for residually non-algebraic prolongations of υ0 to K0(x).
is an inclusion of totally ordered abelian groups with [G1: G0] < ∞ such that G is the direct sum of G1 and an infinite cyclic group. It is proved that there exists an (explicitly constructible) valuation υ of K0(x) extending υ0 such that the value group of υ is G and its residue field is k, where k is a given finite extension of k0. This is analogous to a result of Matignon and Ohm [2, Corollary 3.2] for residually non-algebraic prolongations of υ0 to K0(x).
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1991
References
- 1
- Cited by


