Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T11:13:38.489Z Has data issue: false hasContentIssue false
  • English
  • Français

SCHUR MULTIPLICATIVE MAPS ON MATRICES

Part of: Basic linear algebra

Published online by Cambridge University Press:  01 February 2008

SEAN CLARK ,
CHI-KWONG LI  and
ASHWIN RASTOGI
SEAN CLARK
Affiliation:
Department of Mathematics, College of William and Mary, Williamsburg VA 23185-8795, USA (email: [email protected], [email protected], [email protected])
CHI-KWONG LI
Affiliation:
Department of Mathematics, College of William and Mary, Williamsburg VA 23185-8795, USA (email: [email protected], [email protected], [email protected])
ASHWIN RASTOGI
Affiliation:
Department of Mathematics, College of William and Mary, Williamsburg VA 23185-8795, USA (email: [email protected], [email protected], [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The structure of Schur multiplicative maps on matrices over a field is studied. The result is then used to characterize Schur multiplicative maps f satisfying 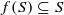for different subsets S of matrices including the set of rank k matrices, the set of singular matrices, and the set of invertible matrices. Characterizations are also obtained for maps on matrices such that Γ(f(A))=Γ(A) for various functions Γ including the rank function, the determinant function, and the elementary symmetric functions of the eigenvalues. These results include analogs of the theorems of Frobenius and Dieudonné on linear maps preserving the determinant functions and linear maps preserving the set of singular matrices, respectively.

Keywords

Schur productSchur multiplicative mapmatricesdeterminantrankeigenvalues

MSC classification

Secondary: 15A03: Vector spaces, linear dependence, rank 15A15: Determinants, permanents, other special matrix functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 77 , Issue 1 , February 2008 , pp. 49 - 72
Copyright
Copyright © Australian Mathematical Society 2008

References

[1]Beasley, L., ‘Linear transformations on matrices: the invariance of the 3rd elementary symmetric function’, Canad. J. Math. 22 (1970), 746–752.CrossRefGoogle Scholar
[2]Beasley, L., ‘Linear transformations on matrices: the invariance of rank k matrices’, Linear Algebra Appl. 107 (1988), 161–167.CrossRefGoogle Scholar
[3]Beasley, L., Li, C.-K. and Pierce, S., ‘Miscellaneous preserver problems. A survey of linear preserver problems’, Linear Multilinear Algebra 22 (1992), 1–2.Google Scholar
[4]Cheung, W. S., Fallat, S. and Li, C. K., ‘Multiplicative preservers on semigroups of matrices’, Linear Algebra Appl. 355 (2002), 173–186.CrossRefGoogle Scholar
[5]Dieudonné, J., ‘Sur une généralization du groupe orthogonal á quatre variables’, Arch. Math. 1 (1949), 282–187.Google Scholar
[6]Dolinar, G. and Šemrl, P., ‘Determinant preserving maps on matrix algebras’, Linear Algebra Appl. 348 (2002), 189–192.CrossRefGoogle Scholar
[7]Frobenius, G., ‘Uber die Darstellung der endichen Gruppen durch linear Substitutionen’, Sitzungsber Deutsch. Akad. Wiss. Berlin (1897), 994–1015.Google Scholar
[8]Hochwald, S. H., ‘Multiplicative maps on matrices that preserve spectrum’, Linear Algebra Appl. 212–213 (1994), 339–351.CrossRefGoogle Scholar
[9]Horn, R., The Hadamard product, matrix theory and application, Phoenix, AZ, 1989, Proceedings of Symposia in Applied Mathematics, 20 (American Mathematical Society, Providence, RI, 1990), pp. 87–169.Google Scholar
[10]James, D., ‘Linear transformations of the second elementary symmetric function’, Linear Multilinear Algebra 10 (1981), 347–349.CrossRefGoogle Scholar
[11]Jodeit, M. Jr and Lam, T. Y., ‘Multiplicative maps of matrix semigroups’, Arch. Math. 20 (1969), 10–16.CrossRefGoogle Scholar
[12]Li, C. K. and Pierce, S., ‘Linear preserver problems’, Amer. Math. Monthly 108 (2001), 591–605.CrossRefGoogle Scholar
[13]Marcus, M. and Purves, R., ‘Linear transformations on algebras of matrices II: The invariance of the elementary symmetric functions’, Canad. J. Math. 11 (1959), 383–396.CrossRefGoogle Scholar
[14]Pierce, S. and Watkins, W., ‘Invariants of linear maps on matrix algebras’, J. Reine Angew. Math. 305 (1978), 60–64.Google Scholar
[15]Šemrl, P., ‘Maps on matrix spaces’, Linear Algebra Appl. 413 (2006), 364–393.CrossRefGoogle Scholar
[16]Tan, V. and Wang, F., ‘On determinant preserver problems’, Linear Algebra Appl. 369 (2003), 311–317.CrossRefGoogle Scholar