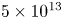doi:10.1017/jfm.2024.484 Song et al. Direct numerical simulations of rapidly rotating Rayleigh–Bénard convection with Rayleigh number up to 5 × 1013
JFM Papers
Near-tip correction functions for the actuator line method to improve the predicted lift and drag distributions
-
- Published online by Cambridge University Press:
- 29 July 2024, A1
-
- Article
-
- You have access
- HTML
- Export citation
A crystallographic approach to symmetry-breaking in fluid layers
-
- Published online by Cambridge University Press:
- 29 July 2024, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct numerical simulations of rapidly rotating Rayleigh–Bénard convection with Rayleigh number up to $5\times 10^{13}$
-
- Published online by Cambridge University Press:
- 29 July 2024, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Microlayer in nucleate boiling seen as Landau–Levich film with dewetting and evaporation
-
- Published online by Cambridge University Press:
- 29 July 2024, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the streamwise velocity variance in the near-wall region of turbulent flows
-
- Published online by Cambridge University Press:
- 29 July 2024, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two- and three-dimensional wake transitions of a rectangular cylinder and resultant hydrodynamic effects
-
- Published online by Cambridge University Press:
- 29 July 2024, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Liouville-type theorems for the Taylor–Couette–Poiseuille flow of the stationary Navier–Stokes equations
-
- Published online by Cambridge University Press:
- 29 July 2024, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability of triple-diffusive convection in a vertical porous layer
-
- Published online by Cambridge University Press:
- 29 July 2024, A8
-
- Article
-
- You have access
- HTML
- Export citation
Onset of convection cells in a horizontally rotating cylinder partially filled with liquid
-
- Published online by Cambridge University Press:
- 29 July 2024, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The influence of hypersonic free-stream conicity on the flow over a sphere
-
- Published online by Cambridge University Press:
- 29 July 2024, A10
-
- Article
-
- You have access
- HTML
- Export citation
Dynamics and fluid–structure interaction in turbulent flows within and above flexible canopies
-
- Published online by Cambridge University Press:
- 29 July 2024, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A high-speed tandem hydrofoil cascade
-
- Published online by Cambridge University Press:
- 29 July 2024, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall turbulence perturbed by a bump with organized small-scale roughness: flow statistics
-
- Published online by Cambridge University Press:
- 29 July 2024, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A model for drift velocity mediated scalar eddy diffusivity in homogeneous turbulent flows
-
- Published online by Cambridge University Press:
- 29 July 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wall-wake laws for the mean velocity and the turbulence
-
- Published online by Cambridge University Press:
- 29 July 2024, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variability of convection velocities and structure inclination angles in wall-bounded turbulence
-
- Published online by Cambridge University Press:
- 29 July 2024, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
General model for segregation forces in flowing granular mixtures
-
- Published online by Cambridge University Press:
- 29 July 2024, A17
-
- Article
-
- You have access
- HTML
- Export citation
Operating principles of peristaltic pumping through a dense array of valves
-
- Published online by Cambridge University Press:
- 29 July 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coherent structures in stably stratified wall-bounded turbulent flows
-
- Published online by Cambridge University Press:
- 29 July 2024, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reynolds number effects in shock-wave/turbulent boundary-layer interactions
-
- Published online by Cambridge University Press:
- 29 July 2024, A20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation