No CrossRef data available.
Published online by Cambridge University Press: 29 July 2024
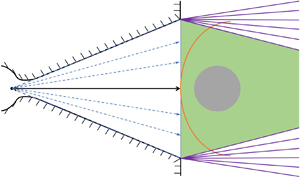
The influence of free-stream conicity on the various aspects of the flow over a spherical test model is examined using both analytical and numerical methods. For the analytical method, a simple closed-form analytical model is assembled. Six different free-stream conditions with different Mach numbers, Reynolds numbers and thermochemistry are tested at four different degrees of conicity corresponding to those which can realistically be encountered in experiments. It is found that the results around the stagnation point are mostly insensitive to the flow condition and gas type, except for some mild non-equilibrium effects, and excellent agreement between the analytical and numerical results exists. The shock stand-off distance on the stagnation streamline is shown to decrease with increasing conicity. This decrease increases the tangential velocity gradient at the stagnation point, increasing the stagnation point heat flux and decreasing the stagnation point boundary layer thickness. The free-stream conicity is also found to alter the normalized distributions of the shock stand-off distance, heat flux, surface pressure and boundary layer thickness with the angle from the stagnation point. In general, increasing the conicity magnifies the slope of these distributions. Regarding the boundary layer transition, it is found that, if it occurs in a uniform free stream, it would also occur in a conical free stream, albeit with the transition point shifted upstream closer to the stagnation point due to the increase in the boundary layer edge tangential velocity. Overall, considering the relevant experimental uncertainties, corrections for free-stream conicity are generally recommended when larger test models are used.