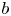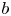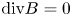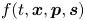Letter
Constrained stellarator coil curvature optimization with FOCUS
- Part of:
-
- Published online by Cambridge University Press:
- 09 March 2021, 175870201
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Letter
Regulation of the normalized rate of driven magnetic reconnection through shocked flux pileup
-
- Published online by Cambridge University Press:
- 29 June 2021, 175870301
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Review Article
The self-focusing condition of a charged particle beam in a resistive plasma
-
- Published online by Cambridge University Press:
- 18 October 2021, 155870501
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Lecture Notes
Magnetohydrodynamics of protoplanetary discs
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2021, 205870101
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Research Article
Extraordinary and upper-hybrid waves in spin quantum magnetoplasmas with vacuum polarization effect
-
- Published online by Cambridge University Press:
- 13 July 2021, 755870401
Letter
Exact nonlinear solutions for three-dimensional Alfvén-wave packets in relativistic magnetohydrodynamics
- Part of:
-
- Published online by Cambridge University Press:
- 21 December 2021, 175870601
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Research Article
The magnetic helicity density patterns from non-axisymmetric solar dynamo
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2021, 775870101
Letter
Comment on “Stepped pressure profile equilibria in cylindrical plasmas via partial Taylor relaxation” [J. Plasma Physics (2006), vol. 72, part 6, pp. 1167–1171]
-
- Published online by Cambridge University Press:
- 05 April 2021, 175870202
Research Article
Phase transition to blob-hole coherent structure in the Hasegawa–Mima model for plasmas
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2021, 835870601
A structure-preserving finite element method for compressible ideal and resistive magnetohydrodynamics
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2021, 835870501
On the violation of the zeroth law of turbulence in space plasmas
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2021, 535870301
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
An energy and momentum conserving collisional bracket for the guiding-centre Vlasov–Maxwell–Landau model
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2021, 835870401
Letter
Corrigendum: ‘Stepped pressure profile equilibria in cylindrical plasmas via partial Taylor relaxation [J. Plasma Physics (2006), vol. 72, part 6, pp. 1167–1171].’
-
- Published online by Cambridge University Press:
- 06 May 2021, 175870203
Research Article
Lane dynamics in pair-ion plasmas: effect of obstacle and geometric aspect ratio
-
- Published online by Cambridge University Press:
- 05 November 2021, 905870601
Hamiltonian kinetic-Hall magnetohydrodynamics with fluid and kinetic ions in the current and pressure coupling schemes
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2021, 835870502
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Koopman wavefunctions and Clebsch variables in Vlasov–Maxwell kinetic theory
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2021, 835870402
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Geometric particle-in-cell methods for the Vlasov–Maxwell equations with spin effects
- Part of:
-
- Published online by Cambridge University Press:
- 28 May 2021, 825870301
Local and global properties of energy transfer in models of plasma turbulence
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2021, 825870101
Hamiltonian reduction of Vlasov–Maxwell to a dark slow manifold
- Part of:
-
- Published online by Cambridge University Press:
- 08 June 2021, 835870301
Scattering of radiofrequency waves by randomly modulated density interfaces in the edge of fusion plasmas
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2021, 855870401
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service