Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T20:53:36.100Z Has data issue: false hasContentIssue false
  • English
  • Français

A structure-preserving finite element method for compressible ideal and resistive magnetohydrodynamics

Part of: Hamiltonian Methods in Plasma Physics

Published online by Cambridge University Press:  17 September 2021

Evan S. Gawlik Open the ORCID record for Evan S. Gawlik [Opens in a new window]  and
François Gay-Balmaz Open the ORCID record for François Gay-Balmaz [Opens in a new window]
Evan S. Gawlik
Affiliation:
Department of Mathematics, University of Hawai‘i at Mānoa
François Gay-Balmaz*
Affiliation:
CNRS - LMD, Ecole Normale Supérieure, Paris
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a structure-preserving finite element method and time-stepping scheme for compressible barotropic magnetohydrodynamics both in the ideal and resistive cases, and in the presence of viscosity. The method is deduced from the geometric variational formulation of the equations. 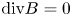It preserves the balance laws governing the evolution of total energy and magnetic helicity, and preserves mass and the constraint $\text {div}B = 0$ to machine precision, both at the spatially and temporally discrete levels. In particular, conservation of energy and magnetic helicity hold at the discrete levels in the ideal case. It is observed that cross-helicity is well conserved in our simulation in the ideal case.

Keywords

plasma simulationplasma dynamics
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 5 , October 2021 , 835870501
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon Press, Oxford University Press.Google Scholar
Ding, Q. & Mao, S. 2020 A convergent finite element method for the compressible magnetohydrodynamics system. J. Sci. Comput. 82 (21).CrossRefGoogle Scholar
Gawlik, E.S. & Gay-Balmaz, F. 2020 a A conservative finite element method for the incompressible Euler equations with variable density. J. Comput. Phys. 412, 109439.CrossRefGoogle Scholar
Gawlik, E.S. & Gay-Balmaz, F. 2020 b A variational finite element discretization of compressible flow. Found. Comput. Math. 21, 961–1001.CrossRefGoogle Scholar
Gawlik, E.S. & Gay-Balmaz, F. 2021 A finite element method for MHD that preserves energy, cross-helicity, magnetic helicity, incompressibility, and $\text {div}B=0$. arXiv:2012.04122.Google Scholar
Gawlik, E.S., Mullen, P., Pavlov, D., Marsden, J.E. & Desbrun, M. 2011 Geometric, variational discretization of continuum theories. Phys. D: Nonlinear Phenom. 240 (21), 1724–1760.CrossRefGoogle Scholar
Hiptmair, R., Li, L., Mao, S. & Zheng, W. 2018 A fully divergence-free finite element method for magnetohydrodynamic equations. Math. Models Meth. Appl. Sci. 28 (04), 659–695.CrossRefGoogle Scholar
Holm, D., Marsden, J. & Ratiu, T. 1998 The Euler-Poincaré equations and semidirect products with applications to continuum theories. Adv. Maths 137, 1–81.CrossRefGoogle Scholar
Hu, K., Lee, Y.-J. & Xu, J. 2021 Helicity-conservative finite element discretization for incompressible MHD systems. J. Comput. Phys. 436, 110284.CrossRefGoogle Scholar
Hu, K., Ma, Y. & Xu, J. 2017 Stable finite element methods preserving $\nabla \cdot {B}=0$ exactly for MHD models. Numer. Math. 135 (2).CrossRefGoogle Scholar
Hu, K. & Xu, J. 2019 Structure-preserving finite element methods for stationary MHD models. Math. Comput. 88 (316), 553–581.CrossRefGoogle Scholar
Kraus, M. & Maj, O. 2017 Variational integrators for ideal magnetohydrodynamics. arXiv:1707.03227.Google Scholar
Liu, J.-G. & Wang, W.-C. 2001 An energy-preserving MAC-Yee scheme for the incompressible MHD equation. J. Comput. Phys. 174 (1), 12–37.CrossRefGoogle Scholar