Let K, K′ be two centrally symmetric convex bodies in En, with their centres at the origin o. Let Vr denote the r-dimensional volume function. A problem of H. Busemann and C. M. Petty [1], see also, H. Busemann [2] asks:—
“If, for each (n − 1)-dimensional subspace L of En,
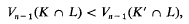
does it follow that
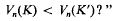
If n = 2 or, if K is an ellipsoid, then Busemann [3] shows that it does follow. However we will show that, at least for n ≥ 12, the result does not hold for general centrally symmetric convex bodies K, even if K′ is an ellipsoid. We do not construct the counter example explicitly; instead we use a probabilistic argument to establish its existence.