Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Masser, D. W.
1978.
Diophantine approximation and lattices with complex multiplication.
Inventiones Mathematicae,
Vol. 45,
Issue. 1,
p.
61.
Bijlsma, A.
1982.
Simultaneous approximation of the coordinates of algebraic points of abelian functions.
Indagationes Mathematicae (Proceedings),
Vol. 85,
Issue. 3,
p.
265.
Васильев, К Г
and
Vasil'ev, K G
1996.
Об алгебраической независимости периодов абелевых интегралов.
Математические заметки,
Vol. 60,
Issue. 5,
p.
681.
Vasil'ev, K. G.
1996.
Algebraic independence of the periods of abelian integrals.
Mathematical Notes,
Vol. 60,
Issue. 5,
p.
510.
Waldschmidt, Michel
2008.
Surveys in Number Theory.
Vol. 17,
Issue. ,
p.
1.


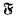 of Abelian functions on the quotient space C
of Abelian functions on the quotient space C