No CrossRef data available.
Article contents
A property of polynomials over a finite field
Published online by Cambridge University Press: 26 February 2010
Extract
Let q be a power of an odd prime, [q] denote the Galois field GF(q) and write X(x) = xq − x. Let f(x) be a polynomial, having no linear factors, over [q], of positive degree, and write 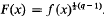 . Consider the continued fraction expansions
. Consider the continued fraction expansions
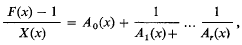
and
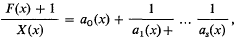
where the Ai(x) and aj,(x) are polynomials over [q] of degree ≥ 1 (if i ≥ 1, j ≥ 1). Plainly A0(x) = ao(x). Suppose that n = nf is the integer denned uniquely as the largest m such that
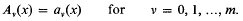
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1975


