Published online by Cambridge University Press: 26 February 2010
We shall prove the following
THEOREM 1. Let α1, …, αn be any positive algebraic numbers and let u1…, un, ν be positive integers, relatively prime in pairs, such that ν ≥ 2 and ui > v for at least one i (1 ≤ i ≤ n). Then for every ε > 0 there are only a finite number of positive integers v such that the inequality
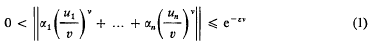
is satisfied, where for real α we understand by ‖α‖ the distance of α from the nearest integer.