An optimal microswimmer with a given geometry has a surface velocity profile that minimises energy dissipation for a given swimming speed. An axisymmetric swimmer can be puller-, pusher- or neutral-type depending on the sign of the stresslet strength. We numerically investigate the type of optimal surface-driven active microswimmers using a minimum dissipation theorem for optimum microswimmers. We examine the hydrodynamic resistance and stresslet strength with nonlinear dependence on various deformation modes. Optimum microswimmers with fore-and-aft symmetry exhibit neutral-type behaviour. Asymmetrical geometries exhibit pusher-, puller- or neutral-type behaviour, depending on the dominant deformation mode and the nonlinear dependence of the stresslet for an optimum microswimmer on deformation mode and amplitude.

The temporal characteristics of fully localised turbulent bands in transitional channel flow remains unclear due to the difficulty in resolving the large length and time scales involved. Here, we tackle this problem by performing statistical lifetime studies in sufficiently large computational domains. The results show signs of stochastic memoryless decay of a fully localised band, suggesting a chaotic-saddle behaviour of the entire band as a coherent entity. Although the mean lifetime of a turbulent band was reported to increase with the band length, our data suggest that it saturates at a certain length. This saturation results in a characteristic lifetime for a fully developed band with a changing length due to the intermittent chipping and decay of turbulence at the upstream end. This memoryless behaviour is observed down to Reynolds number $Re=630$ in our study and we propose that the onset of the memoryless behaviour is in the range of $Re\simeq 620{-}630$. Our data also show that the time it takes for a perturbed flow to enter the saddle, i.e. to start behaving memorylessly, can be thousands of convective time units, which is comparable to the maximum achievable observation time in existing channel set-ups and may pose difficulties for experiments.

Double-diffusive convection can arise when the fluid density is set by multiple species which diffuse at different rates. Different flow regimes are possible depending on the distribution of the diffusing species, including salt fingering and diffusive convection. Flows arising from diffusive convection commonly exhibit step-like density profiles with sharp density interfaces separated by well-mixed layers. The formation of density layers is also seen in stratified turbulence, where a framework based on sorted density coordinates (Winters & D’Asaro 1996 J. Fluid Mech. 317, 179–193) has been used to diagnose layer formation (Zhou et al. 2017 J. Fluid Mech. 823, 198–229; Taylor & Zhou 2017 J. Fluid Mech. 823, R5). In this framework, the evolution of the sorted density profile can be expressed solely in terms of the eddy diffusivity, $\kappa _e$. Here, we use the same framework to diagnose layer formation in two-dimensional simulations of double-diffusive convection. We show that $\kappa _e$ is negative everywhere, with the antidiffusive effect strongest in ‘well-mixed’ layers where a positive diffusion coefficient may be expected. By considering a decomposition of the budget of the square of the Brunt-Väisälä frequency $\partial N^2_*/\partial t$, we demonstrate that the density layers are maintained by fundamentally different processes than in single-component stratified turbulence. In more complicated flows where stratified turbulence and double-diffusive convection can coexist, this framework could provide a method to distinguish between the mechanisms responsible for generating density layers.

Wall turbulence consists of various sizes of vortical structures that induce flow circulation around a wide range of closed Eulerian loops. Here we investigate the multiscale properties of circulation around such loops in statistically homogeneous planes parallel to the wall. Using a high-resolution direct numerical simulation database of turbulent channels at Reynolds numbers of $Re_\tau =180$, 550, 1000 and 5200, circulation statistics are obtained in planes at different wall-normal heights. Intermittency of circulation in the planes of the outer flow ($y^+ \gtrsim 0.1Re_\tau$) takes the form of universal bifractality as in homogeneous and isotropic turbulence. The bifractal character simplifies to space-filling character close to the wall, with scaling exponents that are linear in the moment order, and lower than those given by the Kolmogorov paradigm. The probability density functions of circulation are long-tailed in the outer bifractal region, with evidence showing their invariance with respect to the loop aspect ratio, while those in the inner region are closely Gaussian. The unifractality near the wall implies that the circulation there is not intermittent in character.

Many fluid flow configurations nominally contain symmetries, which are always imperfect in real systems. In this study, we reduce the degree of rotational symmetry and break the mirror symmetry of an annular combustor’s thermoacoustic model by using non-uniform flame response distributions. It is known that, in the linear regime, asymmetries lift the degeneracy of some azimuthal thermoacoustic eigenvalues, which are nominally degenerate in the symmetric case. In this work, we prove that a second asymmetric perturbation, which does not restore any trivial symmetry, can be exploited to create an exceptional point (EP). If the only source of asymmetry is the non-uniform distribution of flame responses, at this symmetry-breaking induced EP the single remaining eigenvector is a perfectly spinning mode. We demonstrate that symmetry-breaking induced EPs may be linearly unstable. For an EP obtained for vanishingly small asymmetric perturbations, the linearly stable/unstable nature of the EP follows that of the degenerate eigenvalue of the perfectly symmetric system. Our results are derived theoretically with a low-order model, and validated on a state-space model extracted from experimental data.

Experimental and numerical observations in turbulent shear flows point to the persistence of the anisotropy imprinted by the large-scale velocity gradient down to the smallest scales of turbulence. This is reminiscent of the strong anisotropy induced by a mean passive scalar gradient, which manifests itself by the ‘ramp–cliff’ structures. In the shear flow problem, the anisotropy can be characterised by the odd-order moments of $\partial _y u$, where $u$ is the fluctuating streamwise velocity component, and 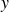$y$ is the direction of mean shear. Here, we extend the approach proposed by Buaria et al. (Phys. Rev. Lett., 126, 034504, 2021) for the passive scalar fields, and postulate that fronts of width $\delta \sim \eta Re_\lambda ^{1/4}$, where $\eta$ is the Kolmogorov length scale, and $Re_\lambda$ is the Taylor-based Reynolds number, explain the observed small-scale anisotropy for shear flows. This model is supported by the collapse of the positive tails of the probability density functions (PDFs) of $(\partial _y u)/(u^{\prime }/\delta )$ in turbulent homogeneous shear flows (THSF) when the PDFs are normalised by $\delta /L$, where $u^{\prime }$ is the root-mean-square of $u$ and $L$ is the integral length scale. The predictions of this model for the odd-order moments of $\partial _y u$ in THSF agree well with direct numerical simulation (DNS) and experimental results. Moreover, the extension of our analysis to the log-layer of turbulent channel flows (TCF) leads to the prediction that the odd-order moments of order $p (p \gt 1)$ of $\partial _y u$ have power-law dependencies on the wall distance $y^{+}$: $\langle (\partial _y u)^p \rangle /\langle (\partial _y u)^2 \rangle ^{p/2} \sim (y^{+})^{(p-5)/8}$, which is consistent with DNS results.

A single particle representation of a self-propelled microorganism in a viscous incompressible fluid is derived based on regularised Stokeslets in three dimensions. The formulation is developed from a limiting process in which two regularised Stokeslets of equal and opposite strength but with different size regularisation parameters approach each other. A parameter that captures the size difference in regularisation provides the asymmetry needed for propulsion. We show that the resulting limit is the superposition of a regularised stresslet and a potential dipole. The model framework is then explored relative to the model parameters to provide insight into their selection. The particular case of two identical particles swimming next to each other is presented and their stability is investigated. Additional flow characteristics are incorporated into the modelling framework with in the addition of a rotlet double to characterise rotational flows present during swimming. Lastly, we show the versatility of deriving the model in the method of regularised Stokeslets framework to model wall effects of an infinite plane wall using the method of images.

Randomness is one of the most important characteristics of turbulence, but its origin remains an open question. By means of a ‘thought experiment’ via several clean numerical experiments based on the Navier–Stokes equations for two-dimensional turbulent Kolmogorov flow, we reveal a new phenomenon, which we call the ‘noise-expansion cascade’ whereby all micro-level noises/disturbances at different orders of magnitudes in the initial condition of Navier–Stokes equations enlarge consistently, say, one by one like an inverse cascade, to macro level. More importantly, each noise/disturbance input may greatly change the macro-level characteristics and statistics of the resulting turbulence, clearly indicating that micro-level noise/disturbance might have great influence on macro-level characteristics and statistics of turbulence. In addition, the noise-expansion cascade closely connects randomness of micro-level noise/disturbance and macro-level disorder of turbulence, thus revealing an origin of randomness of turbulence. This also highly suggests that unavoidable thermal fluctuations must be considered when simulating turbulence, even if such fluctuations are several orders of magnitudes smaller than other external environmental disturbances. We hope that the ‘noise-expansion cascade’, as a fundamental property of the Navier–Stokes equations, could greatly deepen our understandings about turbulence, and also be helpful for attacking the fourth millennium problem posed by the Clay Mathematics Institute in 2000.

Although active flow control based on deep reinforcement learning (DRL) has been demonstrated extensively in numerical environments, practical implementation of real-time DRL control in experiments remains challenging, largely because of the critical time requirement imposed on data acquisition and neural-network computation. In this study, a high-speed field-programmable gate array (FPGA) -based experimental DRL (FeDRL) control framework is developed, capable of achieving a control frequency of 1–10 kHz, two orders higher than that of the existing CPU-based framework (10 Hz). The feasibility of the FeDRL framework is tested in a rather challenging case of supersonic backward-facing step flow at Mach 2, with an array of plasma synthetic jets and a hot-wire acting as the actuator and sensor, respectively. The closed-loop control law is represented by a radial basis function network and optimised by a classical value-based algorithm (i.e. deep Q-network). Results show that, with only ten seconds of training, the agent is able to find a satisfying control law that increases the mixing in the shear layer by 21.2 %. Such a high training efficiency has never been reported in previous experiments (typical time cost: hours).

A millimetric droplet may bounce and self-propel across the surface of a vertically vibrating liquid bath, guided by the slope of its accompanying Faraday wave field. The ‘walker’, consisting of a droplet dressed in a quasi-monochromatic wave form, is a spatially extended object that exhibits many phenomena previously thought exclusive to the quantum realm. While the walker dynamics can be remarkably complex, steady and periodic states arise in which the energy added by the bath vibration necessarily balances that dissipated by viscous effects. The system energetics may then be characterised in terms of the exchange between the bouncing droplet and its guiding or ‘pilot’ wave. We here characterise this energy exchange by means of a theoretical investigation into the dynamics of the pilot-wave system when time-averaged over one bouncing period. Specifically, we derive simple formulae characterising the dependence of the droplet’s gravitational potential energy and wave energy on the droplet speed. Doing so makes clear the partitioning between the gravitational, wave and kinetic energies of walking droplets in a number of steady, periodic and statistically steady dynamical states. We demonstrate that this partitioning depends exclusively on the ratio of the droplet speed to its speed limit.

This study explores an interesting fluid–structure interaction scenario: the flow past a flexible filament fixed at two ends. The dynamic performance of the filament under various inclination angles ($\theta$) was numerically investigated using the immersed boundary method. The motion of the filament in the $\theta$–$Lr$ space was categorised into three flapping modes and two stationary modes, where $Lr$ is the ratio of filament length to the distance between its two ends. The flow fields for each mode and their transitions were introduced. A more in-depth analysis was carried out for flapping at a large angle (FLA mode), which is widely present in the $\theta$–$Lr$ space. The maximum width $W$ of the time-averaged shape of the filament has been shown to strongly correlate with the flapping frequency. After non-dimensionalising based on $W$, the flapping frequency shows little variation across different $Lr$ and $\theta$. Moreover, two types of lift variation process were also identified. Finally, the total lift, drag and lift-to-drag ratio of the system were studied. Short filaments, such as those with $Lr\leqslant 1.5$, were shown to significantly increase lift and the lift-to-drag ratio over a wide range of $\theta$ compared with a rigid plate. Flow field analysis concluded that the increases in pressure difference on both sides of the filament, along with the upper part of the flexible filament having a normal direction closer to the $y$ direction, were the primary reasons for the increase in lift and lift-to-drag ratio. This study can provide some guidance for the potential applications of flexible structures.

Analytical expressions are derived for the velocity field, and effective slip lengths, associated with pressure-driven longitudinal flow in a circular superhydrophobic pipe whose boundary is patterned with a general arrangement of longitudinal no-shear stripes not necessarily possessing any rotational symmetry. First, the flow in a superhydrophobic pipe with $M$ different no-shear stripes in general position is found for $M=1, 2, 3$. The method, which is based on use of so-called prime functions, is such that with these cases covered, generalisation to any $M \geqslant 1$ follows in a straightforward manner. It is shown how any one of these solutions can be generalised to solve for flow along superhydrophobic pipes where that pattern of $M$ menisci is repeated $N \geqslant 1$ times around the boundary in a rotational symmetric arrangement. The work provides an extension of the canonical pipe flow solution for an $N$-fold rotationally symmetric pattern of no-shear stripes due to Philip (Angew. Math. Phys., vol. 23, 1972, pp. 353–372). The novel solution method, and the solutions that it produces, have significance for a wide range of mixed boundary value problems involving Poisson’s equation arising in other applications.

The interaction between porous structures and flows with mean and oscillatory components has many applications in fluid dynamics. One such application is the hydrodynamic forces on offshore jacket structures from waves and current, which have been shown to give a significant blockage effect, leading to a reduction in drag forces. To better understand this, we derived analytical expressions that describe the effect of current on drag forces from large waves, and conducted experiments that measured forces on a model jacket in collinear waves and currents. We utilised symmetry and phase-inversion techniques, relying on the underlying physics of wave structure interaction, to separate Morison drag and inertia-type forces and to decompose these forces into their respective frequency harmonics. We find that the odd harmonics of the drag force mostly contain the loads from waves, while even harmonics vary much more rapidly with the current speed flowing through the jacket. At the time of peak force, these current speeds were estimated to be 40 % of the undisturbed current and 50 % of the industry-standard estimates, a result that has significant implications for design and re-assessment of jackets. At times away from the peak force, when there are no waves and only current, the blockage effects are reduced. Hence, the variation in blocked current speeds appears to occur on a relatively fast time scale similar to the compact wave envelope. These findings may be generalisable to any jacket-type structure in flows with mean and high Keulegan–Carpenter number oscillatory components.

When a drop impacts a solid substrate or a thin liquid film, a thin gas disc is entrapped due to surface tension, the gas disc retracting into one or several bubbles. While the evolution of the gas disc for impact on solid substrate or film of the same fluid as the drop has been largely studied, little is known on how it varies when the liquid of the film is different from that of the drop. We study numerically the latter unexplored area, focusing on the contact between the drop and the film, leading to the formation of an air bubble. The volume of fluid method was adapted to three fluids in the framework of the Basilisk solver. The numerical simulations show that the deformation of the liquid film due to air cushioning plays a crucial role in bubble entrapment. A new model for the contact time and the entrapment geometry was deduced from the case of the impact on a solid substrate. This was done by considering the deformation of the thin immiscible liquid layer during impact depending mainly on its thickness and viscosity. The lubrication of the gas layer was found to be the major effect governing bubble entrapment. However, the film viscosity was also identified as having a critical role in bubble formation and evolution; the magnitude of its influence was also quantified.

The flow over a cambered NACA 65(1)–412 airfoil at $Re\,=\,2\times 10^4$ is described based on a high-order direct numerical simulation. Simulations are run over a range of angles of attack, $\alpha$, where a number of instabilities in the unsteady, three-dimensional flow field are identified. The balance and competing effects of these instabilities are responsible for significant and abrupt (with respect to $\alpha$) changes in flow regime, with measurable consequences in time-averaged, integrated force coefficients, and in the far-wake footprint. At low $\alpha$, the flow is strongly influenced by vortex roll-up from the pressure side at the trailing edge. The interaction of this large-scale structure with shear and three-dimensional modal instabilities in the separated shear layer and associated wake region on the suction side, explains the transitions and bifurcations of the the flow states as $\alpha$ increases. The transition from a separation at low $\alpha$ to reattachment and establishment of a laminar separation bubble at the trailing edge at critical $\alpha$ is driven by instabilities within the separated shear layer that are absent at lower angles. Instabilities of different wavelengths are then shown to pave the path to turbulence in the near wake.

We conducted a series of pore-scale numerical simulations on convective flow in porous media, with a fixed Schmidt number of 400 and a wide range of Rayleigh numbers. The porous media are modeled using regularly arranged square obstacles in a Rayleigh–Bénard (RB) system. As the Rayleigh number increases, the flow transitions from a Darcy-type regime to an RB-type regime, with the corresponding $Sh$–$Ra_D$ relationship shifting from sublinear scaling to the classical 0.3 scaling of RB convection. Here, $Sh$ and $Ra_D$ represent the Sherwood number and the Rayleigh–Darcy number, respectively. For different porosities, the transition begins at approximately $Ra_D = 4000$, at which point the characteristic horizontal scale of the flow field is comparable to the size of a single obstacle unit. When the thickness of the concentration boundary layer is less than approximately one-sixth of the pore spacing, the flow finally enters the RB regime. In the Darcy regime, the scaling exponent of $Sh$ and $Ra_D$ decreases as porosity increases. Based on the Grossman–Lohse theory (J. Fluid Mech. vol. 407, 2000, pp. 27–56; Phys. Rev. Lett. vol. 86, 2001, p. 3316), we provide an explanation for the scaling laws in each regime and highlight the significant impact of mechanical dispersion effects during the development of the plumes. Our findings provide some new insights into the validity range of the Darcy model.

The evolution of a Lamb–Oseen vortex is studied in a stratified rotating fluid under the complete Coriolis force. In a companion paper, it was shown that the non-traditional Coriolis force generates a vertical velocity field and a vertical vorticity anomaly at a critical radius when the Froude number is larger than unity. Below a critical non-traditional Rossby number $\widetilde {Ro}$, a two-dimensional shear instability was next triggered by the vorticity anomaly. Here, we test the robustness of this two-dimensional evolution against small three-dimensional perturbations. Direct numerical simulations (DNS) show that the two-dimensional shear instability then develops only in an intermediate range of non-traditional Rossby numbers for a fixed Reynolds number $Re$. For lower $\widetilde {Ro}$, the instability is three-dimensional. Stability analyses of the flows in the DNS prior to the instability onset fully confirm the existence of these two competing instabilities. In addition, stability analyses of the local theoretical flows at leading order in the critical layer demonstrate that the three-dimensional instability is due to the shear of the vertical velocity. For a given Froude number, its growth rate scales as $Re^{2/3}/\widetilde {Ro}$, whereas the growth rate of the two-dimensional instability depends on $Re/\widetilde {Ro}^2$, provided that the critical layer is smoothed by viscous effects. However, the growth rate of the three-dimensional instability obtained from such local stability analyses agrees quantitatively with those of the DNS flows only if second-order effects due to the traditional Coriolis force and the buoyancy force are taken into account. These effects tend to damp the three-dimensional instability.

We analyse the steady viscoelastic fluid flow in slowly varying contracting channels of arbitrary shape and present a theory based on the lubrication approximation for calculating the flow rate–pressure drop relation at low and high Deborah ($De$) numbers. Unlike most prior theoretical studies leveraging the Oldroyd-B model, we describe the fluid viscoelasticity using a FENE-CR model and examine how the polymer chains’ finite extensibility impacts the pressure drop. We employ the low-Deborah-number lubrication analysis to provide analytical expressions for the pressure drop up to $O(De^4)$. We further consider the ultra-dilute limit and exploit a one-way coupling between the parabolic velocity and elastic stresses to calculate the pressure drop of the FENE-CR fluid for arbitrary values of the Deborah number. Such an approach allows us to elucidate elastic stress contributions governing the pressure drop variations and the effect of finite extensibility for all $De$. We validate our theoretical predictions with two-dimensional numerical simulations and find excellent agreement. We show that, at low Deborah numbers, the pressure drop of the FENE-CR fluid monotonically decreases with $De$, similar to the previous results for the Oldroyd-B and FENE-P fluids. However, at high Deborah numbers, in contrast to a linear decrease for the Oldroyd-B fluid, the pressure drop of the FENE-CR fluid exhibits a non-monotonic variation due to finite extensibility, first decreasing and then increasing with $De$. Nevertheless, even at sufficiently high Deborah numbers, the pressure drop of the FENE-CR fluid in the ultra-dilute and lubrication limits is lower than the corresponding Newtonian pressure drop.

The study examines supersonic square jets in a twin nozzle configuration with the aim of identifying and characterising emergent instability modes during overexpanded operation. Unlike screeching rectangular jets that undergo strong fluctuations normal to the wider jet dimension, the equilateral nature of the exit geometry in square nozzles leads to multiple instability states dictated by shock–turbulence interactions and nozzle operating conditions. Furthermore, strong coupling modes between the jets were identified that led to either phase locked or out of phase interactions of the inner shear layers. Results from experimental studies were examined using spatial and temporal decomposition techniques based on spectral methods to identify the resultants from triadic shock–turbulence interactions. The primary instability mode across both operating conditions were driven by optimal interactions while the harmonics were found to be associated with the suboptimal shock–turbulence interactions.

We report an anomalous capillary phenomenon that reverses typical capillary trapping via nanoparticle suspension and leads to a counterintuitive self-removal of non-aqueous fluid from dead-end structures under weakly hydrophilic conditions. Fluid interfacial energy drives the trapped liquid out by multiscale surfaces: the nanoscopic structure formed by nanoparticle adsorption transfers the molecular-level adsorption film to hydrodynamic film by capillary condensation, and maintains its robust connectivity, then the capillary pressure gradient in the dead-end structures drives trapped fluid motion out of the pore continuously. The developed mathematical models agree well with the measured evolution dynamics of the released fluid. This reversing capillary trapping phenomenon via nanoparticle suspension can be a general event in a random porous medium and could dramatically increase displacement efficiency. Our findings have implications for manipulating capillary pressure gradient direction via nanoparticle suspensions to trap or release the trapped fluid from complex geometries, especially for site-specific delivery, self-cleaning, or self-recover systems.