Let $(W,S)$ be a finite Coxeter group. Kazhdan and Lusztig introduced the concept of $W$-graphs, and Gyoja proved that every irreducible representation of the Iwahori–Hecke algebra $H(W,S)$ can be realized as a $W$-graph. Gyoja defined an auxiliary algebra for this purpose which—to the best of the author’s knowledge—was never explicitly mentioned again in the literature after Gyoja’s proof (although the underlying ideas were reused). The purpose of this paper is to resurrect this $W$-graph algebra, and to study its structure and its modules. A new explicit description of it as a quotient of a certain path algebra is given. A general conjecture is proposed which would imply strong restrictions on the structure of $W$-graphs. This conjecture is then proven for Coxeter groups of type $I_{2}(m)$, $B_{3}$ and $A_{1}$–$A_{4}$.

In this paper, we study the Cauchy problem for the semilinear heat and Schrödinger equations, with the nonlinear term 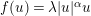$f(u)=\unicode[STIX]{x1D706}|u|^{\unicode[STIX]{x1D6FC}}u$. We show that low regularity of 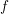$f$ (i.e., 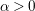$\unicode[STIX]{x1D6FC}>0$ but small) limits the regularity of any possible solution for a certain class of smooth initial data. We employ two different methods, which yield two different types of results. On the one hand, we consider the semilinear equation as a perturbation of the ODE 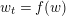$w_{t}=f(w)$. This yields, in particular, an optimal regularity result for the semilinear heat equation in Hölder spaces. In addition, this approach yields ill-posedness results for the nonlinear Schrödinger equation in certain 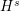$H^{s}$-spaces, which depend on the smallness of 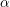$\unicode[STIX]{x1D6FC}$ rather than the scaling properties of the equation. Our second method is to consider the semilinear equation as a perturbation of the linear equation via Duhamel’s formula. This yields, in particular, that if 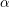$\unicode[STIX]{x1D6FC}$ is sufficiently small and 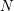$N$ is sufficiently large, then the nonlinear heat equation is ill-posed in 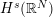$H^{s}(\mathbb{R}^{N})$ for all 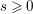$s\geqslant 0$.

We introduce a new method for expanding an abelian category and study it using recollements. In particular, we give a criterion for the existence of cotilting objects. We show, using techniques from noncommutative algebraic geometry, that our construction encompasses the category of coherent sheaves on Geigle–Lenzing weighted projective lines. We apply our construction to some concrete examples and obtain new weighted projective varieties, and analyze the endomorphism algebras of their tilting bundles.

We study the relationship between the reduction number of a primary ideal of a local ring relative to one of its minimal reductions and the multiplicity of the corresponding Sally module. This paper is focused on three goals: (i) to develop a change of rings technique for the Sally module of an ideal to allow extension of results from Cohen–Macaulay rings to more general rings; (ii) to use the fiber of the Sally modules of almost complete intersection ideals to connect its structure to the Cohen–Macaulayness of the special fiber ring; (iii) to extend some of the results of (i) to two-dimensional Buchsbaum rings. Along the way, we provide an explicit realization of the $S_{2}$-fication of arbitrary Buchsbaum rings.

As an application of the boundary parametrization developed in our previous papers, we propose a new method to deduce information on the connected components of the interior of tiles. This gives a systematic way to study the topology of a certain class of self-affine tiles. An example due to Bandt and Gelbrich is examined to prove the efficiency of the method.

We define canonical and $n$-canonical modules of a module-finite algebra over a Noether commutative ring and study their basic properties. Using $n$-canonical modules, we generalize a theorem on $(n,C)$-syzygy by Araya and Iima which generalize a well-known theorem on syzygies by Evans and Griffith. Among others, we prove a noncommutative version of Aoyama’s theorem which states that a canonical module descends with respect to a flat local homomorphism.