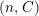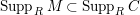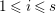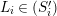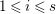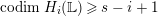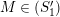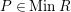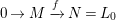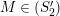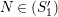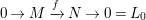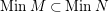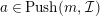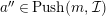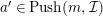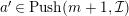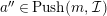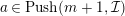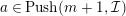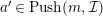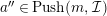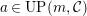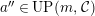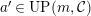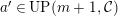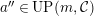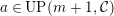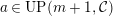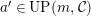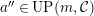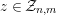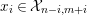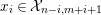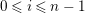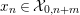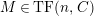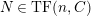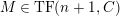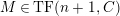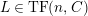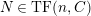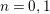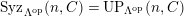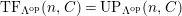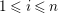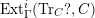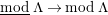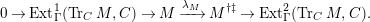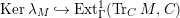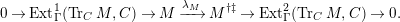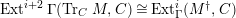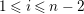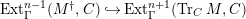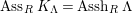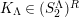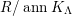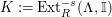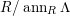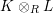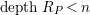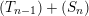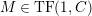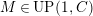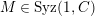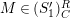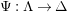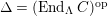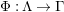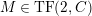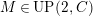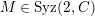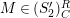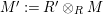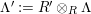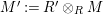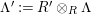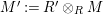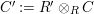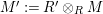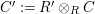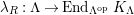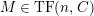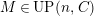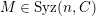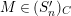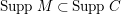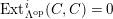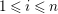1 Introduction
1.1
In [Reference Evans and GriffithEvG], Evans and Griffith proved a criterion of a finite module over a Noetherian commutative ring
![]() $R$
to be an
$R$
to be an
![]() $n$
th syzygy. This was generalized to a theorem on
$n$
th syzygy. This was generalized to a theorem on
![]() $(n,C)$
-syzygy for a semidualizing module
$(n,C)$
-syzygy for a semidualizing module
![]() $C$
over
$C$
over
![]() $R$
by Araya and Iima [Reference Araya and IimaArI]. The main purpose of this paper is to prove a generalization of these results in the following settings: the ring
$R$
by Araya and Iima [Reference Araya and IimaArI]. The main purpose of this paper is to prove a generalization of these results in the following settings: the ring
![]() $R$
is now a finite
$R$
is now a finite
![]() $R$
-algebra
$R$
-algebra
![]() $\unicode[STIX]{x1D6EC}$
, which need not be commutative; and
$\unicode[STIX]{x1D6EC}$
, which need not be commutative; and
![]() $C$
is an
$C$
is an
![]() $n$
-canonical module.
$n$
-canonical module.
1.2
The notion of
![]() $n$
-canonical module was introduced in [Reference HashimotoHas] in an algebro-geometric situation for commutative rings. The criterion for a module to be an
$n$
-canonical module was introduced in [Reference HashimotoHas] in an algebro-geometric situation for commutative rings. The criterion for a module to be an
![]() $n$
th syzygy for
$n$
th syzygy for
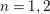 $n=1,2$
by Evans–Griffith was generalized using
$n=1,2$
by Evans–Griffith was generalized using
![]() $n$
-canonical modules there, and the standard ‘codimension-two argument’ (see e.g., [Reference HartshorneHart2, (1.12)]) was also generalized to a theorem on schemes with
$n$
-canonical modules there, and the standard ‘codimension-two argument’ (see e.g., [Reference HartshorneHart2, (1.12)]) was also generalized to a theorem on schemes with
![]() $2$
-canonical modules [Reference HashimotoHas, (7.34)].
$2$
-canonical modules [Reference HashimotoHas, (7.34)].
1.3
Let
![]() $(R,\mathfrak{m})$
be a complete semilocal Noetherian ring, and
$(R,\mathfrak{m})$
be a complete semilocal Noetherian ring, and
![]() $\unicode[STIX]{x1D6EC}\neq 0$
a module-finite
$\unicode[STIX]{x1D6EC}\neq 0$
a module-finite
![]() $R$
-algebra. Let
$R$
-algebra. Let
![]() $\mathbb{I}$
be a dualizing complex of
$\mathbb{I}$
be a dualizing complex of
![]() $R$
. Then
$R$
. Then
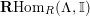 $\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
is a dualizing complex of
$\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
is a dualizing complex of
![]() $\unicode[STIX]{x1D6EC}$
. Its lowest nonvanishing cohomology is denoted by
$\unicode[STIX]{x1D6EC}$
. Its lowest nonvanishing cohomology is denoted by
![]() $K_{\unicode[STIX]{x1D6EC}}$
, and is called the canonical module of
$K_{\unicode[STIX]{x1D6EC}}$
, and is called the canonical module of
![]() $\unicode[STIX]{x1D6EC}$
. If
$\unicode[STIX]{x1D6EC}$
. If
![]() $(R,\mathfrak{m})$
is semilocal but not complete, then a
$(R,\mathfrak{m})$
is semilocal but not complete, then a
![]() $\unicode[STIX]{x1D6EC}$
-bimodule is called a canonical module if it is the canonical module after completion. An
$\unicode[STIX]{x1D6EC}$
-bimodule is called a canonical module if it is the canonical module after completion. An
![]() $n$
-canonical module is defined using the canonical module. A finite right (resp. left, bi-)module
$n$
-canonical module is defined using the canonical module. A finite right (resp. left, bi-)module
![]() $C$
of
$C$
of
![]() $\unicode[STIX]{x1D6EC}$
is said to be
$\unicode[STIX]{x1D6EC}$
is said to be
![]() $n$
-canonical over
$n$
-canonical over
![]() $R$
if (1)
$R$
if (1)
![]() $C$
satisfies Serre’s
$C$
satisfies Serre’s
![]() $(S_{n}^{\prime })$
condition as an
$(S_{n}^{\prime })$
condition as an
![]() $R$
-module, that is, for any
$R$
-module, that is, for any
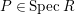 $P\in SpecR$
,
$P\in SpecR$
,
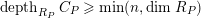 $depth_{R_{P}}C_{P}\geqslant \min (n,\dim R_{P})$
. (2) If
$depth_{R_{P}}C_{P}\geqslant \min (n,\dim R_{P})$
. (2) If
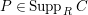 $P\in Supp_{R}C$
with
$P\in Supp_{R}C$
with
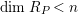 $\dim R_{P}<n$
, then
$\dim R_{P}<n$
, then
![]() $\widehat{C_{P}}$
is isomorphic to
$\widehat{C_{P}}$
is isomorphic to
![]() $K_{\widehat{\unicode[STIX]{x1D6EC}_{P}}}$
as a right (left, bi-) module of
$K_{\widehat{\unicode[STIX]{x1D6EC}_{P}}}$
as a right (left, bi-) module of
![]() $\widehat{\unicode[STIX]{x1D6EC}_{P}}$
, where
$\widehat{\unicode[STIX]{x1D6EC}_{P}}$
, where
![]() $\widehat{\unicode[STIX]{x1D6EC}_{P}}$
is the
$\widehat{\unicode[STIX]{x1D6EC}_{P}}$
is the
![]() $PR_{P}$
-adic completion of
$PR_{P}$
-adic completion of
![]() $\unicode[STIX]{x1D6EC}_{P}$
.
$\unicode[STIX]{x1D6EC}_{P}$
.
1.4
In order to study noncommutative
![]() $n$
-canonical modules, we study a noncommutative analogue of the theory of canonical modules developed by Aoyama [Reference AoyamaAoy], Aoyama–Goto [Reference Aoyama and GotoAoyG], and Ogoma [Reference OgomaOgo] in commutative algebra. Among them, we prove an analogue of Aoyama’s theorem [Reference AoyamaAoy] which states that the canonical module descends with respect to flat homomorphisms (Theorem 7.5).
$n$
-canonical modules, we study a noncommutative analogue of the theory of canonical modules developed by Aoyama [Reference AoyamaAoy], Aoyama–Goto [Reference Aoyama and GotoAoyG], and Ogoma [Reference OgomaOgo] in commutative algebra. Among them, we prove an analogue of Aoyama’s theorem [Reference AoyamaAoy] which states that the canonical module descends with respect to flat homomorphisms (Theorem 7.5).
1.5
Our main theorem is the following.
Theorem 1.6. (Theorem 8.4, cf. [Reference Evans and GriffithEvG, (3.8)], [Reference Araya and IimaArI, (3.1)])
Let
![]() $R$
be a Noetherian commutative ring, and
$R$
be a Noetherian commutative ring, and
![]() $\unicode[STIX]{x1D6EC}$
a module-finite
$\unicode[STIX]{x1D6EC}$
a module-finite
![]() $R$
-algebra, which need not be commutative. Let
$R$
-algebra, which need not be commutative. Let
![]() $n\geqslant 1$
, and
$n\geqslant 1$
, and
![]() $C$
be a right
$C$
be a right
![]() $n$
-canonical
$n$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-module. Set
$\unicode[STIX]{x1D6EC}$
-module. Set
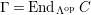 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Let
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Let
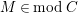 $M\in modC$
. Then the following are equivalent.
$M\in modC$
. Then the following are equivalent.
-
(1)
 $M$
is
$M$
is
 $(n,C)$
-TF.
$(n,C)$
-TF. -
(2)
 $M$
has an
$M$
has an
 $(n,C)$
-universal pushforward.
$(n,C)$
-universal pushforward. -
(3)
 $M$
is an
$M$
is an
 $(n,C)$
-syzygy.
$(n,C)$
-syzygy. -
(4)
 $M$
satisfies the
$M$
satisfies the
 $(S_{n}^{\prime })$
condition as an
$(S_{n}^{\prime })$
condition as an
 $R$
-module, and
$R$
-module, and
 $Supp_{R}M\subset Supp_{R}C$
.
$Supp_{R}M\subset Supp_{R}C$
.
Here we say that
![]() $M$
has an
$M$
has an
![]() $(n,C)$
-universal pushforward if there is an exact sequence
$(n,C)$
-universal pushforward if there is an exact sequence
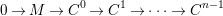 $$\begin{eqnarray}0\rightarrow M\rightarrow C^{0}\rightarrow C^{1}\rightarrow \cdots \rightarrow C^{n-1}\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\rightarrow C^{0}\rightarrow C^{1}\rightarrow \cdots \rightarrow C^{n-1}\end{eqnarray}$$
such that
![]() $C^{i}$
lies in
$C^{i}$
lies in
![]() $addC$
and the sequence is still exact after applying
$addC$
and the sequence is still exact after applying
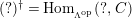 $(?)^{\dagger }= Hom_{_{\unicode[STIX]{x1D6EC}^{op}}}(?,C)$
.
$(?)^{\dagger }= Hom_{_{\unicode[STIX]{x1D6EC}^{op}}}(?,C)$
.
1.7
The
![]() $(n,C)$
-TF condition is a modified version of Takahashi’s
$(n,C)$
-TF condition is a modified version of Takahashi’s
![]() $n$
-
$n$
-
![]() $C$
-torsion freeness [Reference TakahashiTak]. Under the assumptions of the theorem, let
$C$
-torsion freeness [Reference TakahashiTak]. Under the assumptions of the theorem, let
 $(?)^{\dagger }= Hom_{_{\unicode[STIX]{x1D6EC}^{op}}}(?,C)$
,
$(?)^{\dagger }= Hom_{_{\unicode[STIX]{x1D6EC}^{op}}}(?,C)$
,
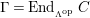 $\unicode[STIX]{x1D6E4}= End_{_{\unicode[STIX]{x1D6EC}^{op}}}C$
, and
$\unicode[STIX]{x1D6E4}= End_{_{\unicode[STIX]{x1D6EC}^{op}}}C$
, and
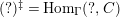 $(?)^{\ddagger }= Hom_{\unicode[STIX]{x1D6E4}}(?,C)$
. We say that
$(?)^{\ddagger }= Hom_{\unicode[STIX]{x1D6E4}}(?,C)$
. We say that
![]() $M$
is
$M$
is
![]() $(1,C)$
-TF (resp.
$(1,C)$
-TF (resp.
![]() $M$
is
$M$
is
![]() $(2,C)$
-TF) if the canonical map
$(2,C)$
-TF) if the canonical map
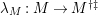 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is injective (resp. bijective). If
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is injective (resp. bijective). If
![]() $n\geqslant 3$
, we say that
$n\geqslant 3$
, we say that
![]() $M$
is
$M$
is
![]() $(n,C)$
-TF if
$(n,C)$
-TF if
![]() $M$
is
$M$
is
![]() $(2,C)$
-TF and
$(2,C)$
-TF and
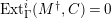 $Ext_{\unicode[STIX]{x1D6E4}}^{i}(M^{\dagger },C)=0$
for
$Ext_{\unicode[STIX]{x1D6E4}}^{i}(M^{\dagger },C)=0$
for
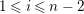 $1\leqslant i\leqslant n-2$
, see Definition 4.5. Even if
$1\leqslant i\leqslant n-2$
, see Definition 4.5. Even if
![]() $\unicode[STIX]{x1D6EC}$
is a commutative ring, a noncommutative ring
$\unicode[STIX]{x1D6EC}$
is a commutative ring, a noncommutative ring
![]() $\unicode[STIX]{x1D6E4}$
appears in a natural way, so even in this case, the definition is slightly different from Takahashi’s original one. We prove that
$\unicode[STIX]{x1D6E4}$
appears in a natural way, so even in this case, the definition is slightly different from Takahashi’s original one. We prove that
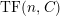 $TF(n,C)$
, the class of modules which satisfy
$TF(n,C)$
, the class of modules which satisfy
![]() $(n,C)$
-TF property, and
$(n,C)$
-TF property, and
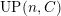 $UP(n,C)$
, the class of modules having
$UP(n,C)$
, the class of modules having
![]() $(n,C)$
-universal pushforwards are equal in general (Lemma 4.7). This is a modified version of Takahashi’s result [Reference TakahashiTak, (3.2)].
$(n,C)$
-universal pushforwards are equal in general (Lemma 4.7). This is a modified version of Takahashi’s result [Reference TakahashiTak, (3.2)].
1.8
As an application of the main theorem, we formulate and prove a different form of the existence of
![]() $n$
-
$n$
-
![]() $C$
-spherical approximations by Takahashi [Reference TakahashiTak], using
$C$
-spherical approximations by Takahashi [Reference TakahashiTak], using
![]() $n$
-canonical modules; see Corollary 8.5 and Corollary 8.6. Our results are not strong enough to deduce [Reference TakahashiTak, Corollary 5.8] in commutative case. For related categorical results, see below.
$n$
-canonical modules; see Corollary 8.5 and Corollary 8.6. Our results are not strong enough to deduce [Reference TakahashiTak, Corollary 5.8] in commutative case. For related categorical results, see below.
1.9
Section 2 is preliminaries on the depth and Serre’s conditions on modules. In Section 3, we discuss
![]() ${\mathcal{X}}_{n,m}$
-approximation, which is a categorical abstraction of approximations of modules appeared in [Reference TakahashiTak]. Everything is done categorically here, and Theorem 3.16 is an abstraction of [Reference TakahashiTak, (3.5)], in view of the fact that
${\mathcal{X}}_{n,m}$
-approximation, which is a categorical abstraction of approximations of modules appeared in [Reference TakahashiTak]. Everything is done categorically here, and Theorem 3.16 is an abstraction of [Reference TakahashiTak, (3.5)], in view of the fact that
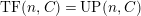 $TF(n,C)= UP(n,C)$
in general (Lemma 4.7). In Section 4, we discuss
$TF(n,C)= UP(n,C)$
in general (Lemma 4.7). In Section 4, we discuss
![]() $(n,C)$
-TF property, and prove Lemma 4.7 and related lemmas. In Section 5, we define the canonical module of a module-finite algebra
$(n,C)$
-TF property, and prove Lemma 4.7 and related lemmas. In Section 5, we define the canonical module of a module-finite algebra
![]() $\unicode[STIX]{x1D6EC}$
over a Noetherian commutative ring
$\unicode[STIX]{x1D6EC}$
over a Noetherian commutative ring
![]() $R$
, and prove some basic properties. In Section 6, we define the
$R$
, and prove some basic properties. In Section 6, we define the
![]() $n$
-canonical module of
$n$
-canonical module of
![]() $\unicode[STIX]{x1D6EC}$
, and prove some basic properties, generalizing some constructions and results in [Reference HashimotoHas, Section 7]. In Section 7, we prove a noncommutative version of Aoyama’s theorem which says that the canonical module descends with respect to flat local homomorphisms (Theorem 7.5). As a corollary, as in the commutative case, we immediately have that a localization of a canonical module is again a canonical module. This is important in Section 8. In Section 8, we prove Theorem 8.4, and the related results on
$\unicode[STIX]{x1D6EC}$
, and prove some basic properties, generalizing some constructions and results in [Reference HashimotoHas, Section 7]. In Section 7, we prove a noncommutative version of Aoyama’s theorem which says that the canonical module descends with respect to flat local homomorphisms (Theorem 7.5). As a corollary, as in the commutative case, we immediately have that a localization of a canonical module is again a canonical module. This is important in Section 8. In Section 8, we prove Theorem 8.4, and the related results on
![]() $n$
-
$n$
-
![]() $C$
-spherical approximations (Corollary 8.5, Corollary 8.6) as its corollaries. Before these, we prove noncommutative analogues of the theorems of Schenzel and Aoyama–Goto [Reference Aoyama and GotoAoyG, (2.2), (2.3)] on the Cohen–Macaulayness of the canonical module (Proposition 8.2 and Corollary 8.3).
$C$
-spherical approximations (Corollary 8.5, Corollary 8.6) as its corollaries. Before these, we prove noncommutative analogues of the theorems of Schenzel and Aoyama–Goto [Reference Aoyama and GotoAoyG, (2.2), (2.3)] on the Cohen–Macaulayness of the canonical module (Proposition 8.2 and Corollary 8.3).
2 Preliminaries
2.1
Unless otherwise specified, a module means a left module. Let
![]() $B$
be a ring.
$B$
be a ring.
![]() $Hom_{B}$
or
$Hom_{B}$
or
![]() $Ext_{B}$
mean the
$Ext_{B}$
mean the
![]() $Hom$
or
$Hom$
or
![]() $Ext$
for left
$Ext$
for left
![]() $B$
-modules.
$B$
-modules.
![]() $B^{op}$
denotes the opposite ring of
$B^{op}$
denotes the opposite ring of
![]() $B$
, so a
$B$
, so a
![]() $B^{op}$
-module is nothing but a right
$B^{op}$
-module is nothing but a right
![]() $B$
-module. Let
$B$
-module. Let
![]() $BMod$
denote the category of
$BMod$
denote the category of
![]() $B$
-modules.
$B$
-modules.
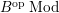 $B^{op} Mod$
is also denoted by
$B^{op} Mod$
is also denoted by
![]() $ModB$
. For a left (resp. right) Noetherian ring
$ModB$
. For a left (resp. right) Noetherian ring
![]() $B$
,
$B$
,
![]() $B{\rm mod}$
(resp.
$B{\rm mod}$
(resp.
![]() ${\rm mod}B$
) denotes the full subcategory of
${\rm mod}B$
) denotes the full subcategory of
![]() $BMod$
(resp.
$BMod$
(resp.
![]() $ModB$
) consisting of finitely generated left (resp. right)
$ModB$
) consisting of finitely generated left (resp. right)
![]() $B$
-modules.
$B$
-modules.
2.2
For derived categories, we employ standard notation found in [Reference HartshorneHart].
For an abelian category
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $D({\mathcal{A}})$
denotes the unbounded derived category of
$D({\mathcal{A}})$
denotes the unbounded derived category of
![]() ${\mathcal{A}}$
. For a plump subcategory (that is, a full subcategory which is closed under kernels, cokernels, and extensions)
${\mathcal{A}}$
. For a plump subcategory (that is, a full subcategory which is closed under kernels, cokernels, and extensions)
![]() ${\mathcal{B}}$
of
${\mathcal{B}}$
of
![]() ${\mathcal{A}}$
,
${\mathcal{A}}$
,
![]() $D_{{\mathcal{B}}}({\mathcal{A}})$
denotes the triangulated subcategory of
$D_{{\mathcal{B}}}({\mathcal{A}})$
denotes the triangulated subcategory of
![]() $D({\mathcal{A}})$
consisting of objects
$D({\mathcal{A}})$
consisting of objects
![]() $\mathbb{F}$
such that
$\mathbb{F}$
such that
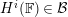 $H^{i}(\mathbb{F})\in {\mathcal{B}}$
for any
$H^{i}(\mathbb{F})\in {\mathcal{B}}$
for any
![]() $i$
. For a ring
$i$
. For a ring
![]() $B$
, we denote
$B$
, we denote
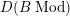 $D(BMod)$
by
$D(BMod)$
by
![]() $D(B)$
, and
$D(B)$
, and
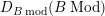 $D_{B mod}(BMod)$
by
$D_{B mod}(BMod)$
by
![]() $D_{fg}(B)$
(if
$D_{fg}(B)$
(if
![]() $B$
is left Noetherian).
$B$
is left Noetherian).
2.3
Throughout the paper, let
![]() $R$
denote a commutative Noetherian ring. If
$R$
denote a commutative Noetherian ring. If
![]() $R$
is semilocal (resp. local) and
$R$
is semilocal (resp. local) and
![]() $\mathfrak{m}$
its Jacobson radical, then we say that
$\mathfrak{m}$
its Jacobson radical, then we say that
![]() $(R,\mathfrak{m})$
is semilocal (resp. local). We say that
$(R,\mathfrak{m})$
is semilocal (resp. local). We say that
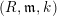 $(R,\mathfrak{m},k)$
is semilocal (resp. local) if
$(R,\mathfrak{m},k)$
is semilocal (resp. local) if
![]() $(R,\mathfrak{m})$
is semilocal (resp. local) and
$(R,\mathfrak{m})$
is semilocal (resp. local) and
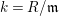 $k=R/\mathfrak{m}$
.
$k=R/\mathfrak{m}$
.
2.4
We set
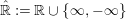 $\hat{\mathbb{R}}:=\mathbb{R}\cup \{\infty ,-\infty \}$
and consider that
$\hat{\mathbb{R}}:=\mathbb{R}\cup \{\infty ,-\infty \}$
and consider that
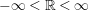 $-\infty <\mathbb{R}<\infty$
. As a convention, for a subset
$-\infty <\mathbb{R}<\infty$
. As a convention, for a subset
![]() $\unicode[STIX]{x1D6E4}$
of
$\unicode[STIX]{x1D6E4}$
of
![]() $\hat{\mathbb{R}}$
,
$\hat{\mathbb{R}}$
,
![]() $\inf \unicode[STIX]{x1D6E4}$
means
$\inf \unicode[STIX]{x1D6E4}$
means
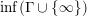 $\inf (\unicode[STIX]{x1D6E4}\cup \{\infty \})$
, which exists uniquely as an element of
$\inf (\unicode[STIX]{x1D6E4}\cup \{\infty \})$
, which exists uniquely as an element of
![]() $\hat{\mathbb{R}}$
. Similarly for
$\hat{\mathbb{R}}$
. Similarly for
![]() $\sup$
.
$\sup$
.
2.5
For an ideal
![]() $I$
of
$I$
of
![]() $R$
and
$R$
and
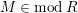 $M\in modR$
, we define
$M\in modR$
, we define
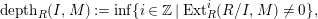 $$\begin{eqnarray}depth_{R}(I,M):=\inf \{i\in \mathbb{Z}\mid Ext_{R}^{i}(R/I,M)\neq 0\},\end{eqnarray}$$
$$\begin{eqnarray}depth_{R}(I,M):=\inf \{i\in \mathbb{Z}\mid Ext_{R}^{i}(R/I,M)\neq 0\},\end{eqnarray}$$
and call it the
![]() $I$
-depth of
$I$
-depth of
![]() $M$
[Reference MatsumuraMat, Section 16]. It is also called the
$M$
[Reference MatsumuraMat, Section 16]. It is also called the
![]() $M$
-grade of
$M$
-grade of
![]() $I$
[Reference Brodmann and SharpBS, (6.2.4)]. When
$I$
[Reference Brodmann and SharpBS, (6.2.4)]. When
![]() $(R,\mathfrak{m})$
is semilocal, we denote
$(R,\mathfrak{m})$
is semilocal, we denote
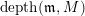 $depth(\mathfrak{m},M)$
by
$depth(\mathfrak{m},M)$
by
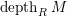 $depth_{R}M$
or
$depth_{R}M$
or
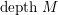 $depthM$
, and call it the depth of
$depthM$
, and call it the depth of
![]() $M$
.
$M$
.
2.6
For a subset
![]() $F$
of
$F$
of
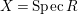 $X= SpecR$
, we define
$X= SpecR$
, we define
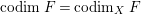 $codimF= codim_{X}F$
, the codimension of
$codimF= codim_{X}F$
, the codimension of
![]() $F$
in
$F$
in
![]() $X$
, by
$X$
, by
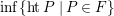 $\inf \{htP\mid P\in F\}$
. So
$\inf \{htP\mid P\in F\}$
. So
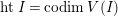 $htI= codimV(I)$
for an ideal
$htI= codimV(I)$
for an ideal
![]() $I$
of
$I$
of
![]() $R$
. For
$R$
. For
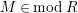 $M\in modR$
, we define
$M\in modR$
, we define
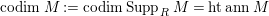 $codimM:= codimSupp_{R}M= htannM$
, where
$codimM:= codimSupp_{R}M= htannM$
, where
![]() $ann$
denotes the annihilator. For
$ann$
denotes the annihilator. For
![]() $n\geqslant 0$
, we denote the set
$n\geqslant 0$
, we denote the set
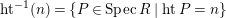 $ht^{-1}(n)=\{P\in SpecR\mid htP=n\}$
by
$ht^{-1}(n)=\{P\in SpecR\mid htP=n\}$
by
![]() $R^{\langle n\rangle }$
. For a subset
$R^{\langle n\rangle }$
. For a subset
![]() $\unicode[STIX]{x1D6E4}$
of
$\unicode[STIX]{x1D6E4}$
of
![]() $\mathbb{Z}$
,
$\mathbb{Z}$
,
![]() $R^{\langle \unicode[STIX]{x1D6E4}\rangle }$
means
$R^{\langle \unicode[STIX]{x1D6E4}\rangle }$
means
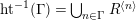 $ht^{-1}(\unicode[STIX]{x1D6E4})=\bigcup _{n\in \unicode[STIX]{x1D6E4}}R^{\langle n\rangle }$
. Moreover, we use notation such as
$ht^{-1}(\unicode[STIX]{x1D6E4})=\bigcup _{n\in \unicode[STIX]{x1D6E4}}R^{\langle n\rangle }$
. Moreover, we use notation such as
![]() $R^{\langle {\leqslant}3\rangle }$
, which stands for
$R^{\langle {\leqslant}3\rangle }$
, which stands for
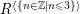 $R^{\langle \{n\in \mathbb{Z}\mid n\leqslant 3\}\rangle }$
, the set of primes of height at most
$R^{\langle \{n\in \mathbb{Z}\mid n\leqslant 3\}\rangle }$
, the set of primes of height at most
![]() $3$
. For
$3$
. For
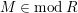 $M\in modR$
, the set of minimal primes of
$M\in modR$
, the set of minimal primes of
![]() $M$
is denoted by
$M$
is denoted by
![]() $MinM$
.
$MinM$
.
We define
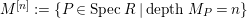 $M^{[n]}:=\{P\in SpecR\mid depthM_{P}=n\}$
. Similarly, we use notation such as
$M^{[n]}:=\{P\in SpecR\mid depthM_{P}=n\}$
. Similarly, we use notation such as
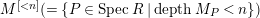 $M^{[{<}n]}(=\{P\in SpecR\mid depthM_{P}<n\})$
.
$M^{[{<}n]}(=\{P\in SpecR\mid depthM_{P}<n\})$
.
2.7
Let
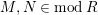 $M,N\in modR$
. We say that
$M,N\in modR$
. We say that
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{N})^{R}$
-condition or
$(S_{n}^{N})^{R}$
-condition or
![]() $(S_{n}^{N})$
-condition if for any
$(S_{n}^{N})$
-condition if for any
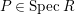 $P\in SpecR$
,
$P\in SpecR$
,
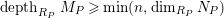 $depth_{R_{P}}M_{P}\geqslant \min (n,\dim _{R_{P}}N_{P})$
. The
$depth_{R_{P}}M_{P}\geqslant \min (n,\dim _{R_{P}}N_{P})$
. The
![]() $(S_{n}^{R})^{R}$
-condition or
$(S_{n}^{R})^{R}$
-condition or
![]() $(S_{n}^{R})$
-condition is simply denoted by
$(S_{n}^{R})$
-condition is simply denoted by
![]() $(S_{n}^{\prime })^{R}$
or
$(S_{n}^{\prime })^{R}$
or
![]() $(S_{n}^{\prime })$
. We say that
$(S_{n}^{\prime })$
. We say that
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n})^{R}$
-condition or
$(S_{n})^{R}$
-condition or
![]() $(S_{n})$
-condition if
$(S_{n})$
-condition if
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{M})$
-condition.
$(S_{n}^{M})$
-condition.
![]() $(S_{n})$
(resp.
$(S_{n})$
(resp.
![]() $(S_{n}^{\prime })$
) is equivalent to say that for any
$(S_{n}^{\prime })$
) is equivalent to say that for any
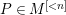 $P\in M^{[{<}n]}$
,
$P\in M^{[{<}n]}$
,
![]() $M_{P}$
is a Cohen–Macaulay (resp. maximal Cohen–Macaulay)
$M_{P}$
is a Cohen–Macaulay (resp. maximal Cohen–Macaulay)
![]() $R_{P}$
-module. That is,
$R_{P}$
-module. That is,
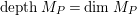 $depthM_{P}=\dim M_{P}$
(resp.
$depthM_{P}=\dim M_{P}$
(resp.
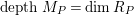 $depthM_{P}=\dim R_{P}$
). We consider that
$depthM_{P}=\dim R_{P}$
). We consider that
![]() $(S_{n}^{N})^{R}$
is a class of modules, and also write
$(S_{n}^{N})^{R}$
is a class of modules, and also write
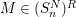 $M\in (S_{n}^{N})^{R}$
(or
$M\in (S_{n}^{N})^{R}$
(or
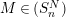 $M\in (S_{n}^{N})$
).
$M\in (S_{n}^{N})$
).
Lemma 2.8. Let
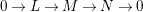 $0\rightarrow L\rightarrow M\rightarrow N\rightarrow 0$
be an exact sequence in
$0\rightarrow L\rightarrow M\rightarrow N\rightarrow 0$
be an exact sequence in
![]() ${\rm mod}R$
, and
${\rm mod}R$
, and
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
-
(1) If
 $L$
and
$L$
and
 $N$
satisfy
$N$
satisfy
 $(S_{n}^{\prime })$
, then
$(S_{n}^{\prime })$
, then
 $M$
satisfies
$M$
satisfies
 $(S_{n}^{\prime })$
.
$(S_{n}^{\prime })$
. -
(2) If
 $N$
satisfies
$N$
satisfies
 $(S_{n-1}^{\prime })$
and
$(S_{n-1}^{\prime })$
and
 $M$
satisfies
$M$
satisfies
 $(S_{n}^{\prime })$
, then
$(S_{n}^{\prime })$
, then
 $L$
satisfies
$L$
satisfies
 $(S_{n}^{\prime })$
.
$(S_{n}^{\prime })$
.
Proof. (1) follows from the depth lemma:
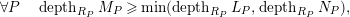 $$\begin{eqnarray}\forall P\quad depth_{R_{P}}M_{P}\geqslant \min (depth_{R_{P}}L_{P},depth_{R_{P}}N_{P}),\end{eqnarray}$$
$$\begin{eqnarray}\forall P\quad depth_{R_{P}}M_{P}\geqslant \min (depth_{R_{P}}L_{P},depth_{R_{P}}N_{P}),\end{eqnarray}$$
and the fact that maximal Cohen–Macaulay modules are closed under extensions. (2) is similar. ◻
Corollary 2.9. Let
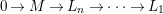 $$\begin{eqnarray}0\rightarrow M\rightarrow L_{n}\rightarrow \cdots \rightarrow L_{1}\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\rightarrow L_{n}\rightarrow \cdots \rightarrow L_{1}\end{eqnarray}$$
be an exact sequence in
![]() ${\rm mod}R$
, and assume that
${\rm mod}R$
, and assume that
![]() $L_{i}$
satisfies
$L_{i}$
satisfies
![]() $(S_{i}^{\prime })$
for
$(S_{i}^{\prime })$
for
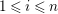 $1\leqslant i\leqslant n$
. Then
$1\leqslant i\leqslant n$
. Then
![]() $M$
satisfies
$M$
satisfies
![]() $(S_{n}^{\prime })$
.
$(S_{n}^{\prime })$
.
Proof. This is proved using Lemma 2.8(2) repeatedly. ◻
Lemma 2.10. (cf. [Reference Iyama and WemyssIW, (3.4)])
Let
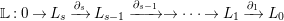 $$\begin{eqnarray}\mathbb{L}:0\rightarrow L_{s}\xrightarrow[{}]{\unicode[STIX]{x2202}_{s}}L_{s-1}\xrightarrow[{}]{\unicode[STIX]{x2202}_{s-1}}\rightarrow \cdots \rightarrow L_{1}\xrightarrow[{}]{\unicode[STIX]{x2202}_{1}}L_{0}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{L}:0\rightarrow L_{s}\xrightarrow[{}]{\unicode[STIX]{x2202}_{s}}L_{s-1}\xrightarrow[{}]{\unicode[STIX]{x2202}_{s-1}}\rightarrow \cdots \rightarrow L_{1}\xrightarrow[{}]{\unicode[STIX]{x2202}_{1}}L_{0}\end{eqnarray}$$
be a complex in
![]() ${\rm mod}R$
such that
${\rm mod}R$
such that
-
(1) For each
 $i\in \mathbb{Z}$
with
$i\in \mathbb{Z}$
with
 $1\leqslant i\leqslant s$
,
$1\leqslant i\leqslant s$
,
 $L_{i}\in (S_{i}^{\prime })$
.
$L_{i}\in (S_{i}^{\prime })$
. -
(2) For each
 $i\in \mathbb{Z}$
with
$i\in \mathbb{Z}$
with
 $1\leqslant i\leqslant s$
,
$1\leqslant i\leqslant s$
,
 $codimH_{i}(\mathbb{L})\geqslant s-i+1$
.
$codimH_{i}(\mathbb{L})\geqslant s-i+1$
.
Then
![]() $\mathbb{L}$
is acyclic.
$\mathbb{L}$
is acyclic.
Proof. Using induction on
![]() $s$
, we may assume that
$s$
, we may assume that
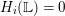 $H_{i}(\mathbb{L})=0$
for
$H_{i}(\mathbb{L})=0$
for
![]() $i>1$
. Assume that
$i>1$
. Assume that
![]() $\mathbb{L}$
is not acyclic. Then
$\mathbb{L}$
is not acyclic. Then
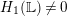 $H_{1}(\mathbb{L})\neq 0$
, and we can take
$H_{1}(\mathbb{L})\neq 0$
, and we can take
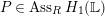 $P\in Ass_{R}H_{1}(\mathbb{L})$
. By assumption,
$P\in Ass_{R}H_{1}(\mathbb{L})$
. By assumption,
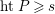 $htP\geqslant s$
. Now localize at
$htP\geqslant s$
. Now localize at
![]() $P$
and considering the complex
$P$
and considering the complex
![]() $\mathbb{L}_{P}$
over
$\mathbb{L}_{P}$
over
![]() $R_{P}$
, we get a contradiction by Acyclicity Lemma [Reference Peskine and SzpiroPS, (1.8)].◻
$R_{P}$
, we get a contradiction by Acyclicity Lemma [Reference Peskine and SzpiroPS, (1.8)].◻
Example 2.11. Let
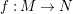 $f:M\rightarrow N$
be a map in
$f:M\rightarrow N$
be a map in
![]() ${\rm mod}R$
.
${\rm mod}R$
.
-
(1) If
 $M\in (S_{1}^{\prime })$
and
$M\in (S_{1}^{\prime })$
and
 $f_{P}$
is injective for
$f_{P}$
is injective for
 $P\in MinR$
, then
$P\in MinR$
, then
 $f$
is injective. To prove this, consider the complex and apply Lemma 2.10.
$f$
is injective. To prove this, consider the complex and apply Lemma 2.10. $$\begin{eqnarray}0\rightarrow M\xrightarrow[{}]{f}N=L_{0}\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\xrightarrow[{}]{f}N=L_{0}\end{eqnarray}$$
-
(2) [Reference Leuschke and WiegandLeW, (5.11)] If
 $M\in (S_{2}^{\prime })$
,
$M\in (S_{2}^{\prime })$
,
 $N\in (S_{1}^{\prime })$
, and
$N\in (S_{1}^{\prime })$
, and
 $f_{P}$
is bijective for primes
$f_{P}$
is bijective for primes
 $P$
of
$P$
of
 $R$
of height at most one, then
$R$
of height at most one, then
 $f$
is bijective. Consider the complex this time.
$f$
is bijective. Consider the complex this time. $$\begin{eqnarray}0\rightarrow M\xrightarrow[{}]{f}N\rightarrow 0=L_{0}\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\xrightarrow[{}]{f}N\rightarrow 0=L_{0}\end{eqnarray}$$
Lemma 2.12. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring, and
$(R,\mathfrak{m})$
be a Noetherian local ring, and
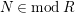 $N\in modR$
. Assume that
$N\in modR$
. Assume that
![]() $N$
satisfies the
$N$
satisfies the
![]() $(S_{n})$
condition. If
$(S_{n})$
condition. If
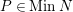 $P\in MinN$
with
$P\in MinN$
with
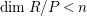 $\dim R/P<n$
, then we have
$\dim R/P<n$
, then we have
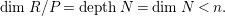 $$\begin{eqnarray}\dim R/P= depthN=\dim N<n.\end{eqnarray}$$
$$\begin{eqnarray}\dim R/P= depthN=\dim N<n.\end{eqnarray}$$
If, moreover,
![]() $N$
satisfies
$N$
satisfies
![]() $(S_{n}^{\prime })$
, then
$(S_{n}^{\prime })$
, then
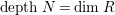 $depthN=\dim R$
.
$depthN=\dim R$
.
Proof. Ischebeck proved that if
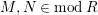 $M,N\in modR$
and
$M,N\in modR$
and
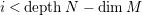 $i< depthN-\dim M$
, then
$i< depthN-\dim M$
, then
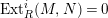 $Ext_{R}^{i}(M,N)=0$
[Reference MatsumuraMat, (17.1)]. As
$Ext_{R}^{i}(M,N)=0$
[Reference MatsumuraMat, (17.1)]. As
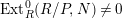 $Ext_{R}^{0}(R/P,N)\neq 0$
, we have that
$Ext_{R}^{0}(R/P,N)\neq 0$
, we have that
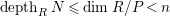 $depth_{R}N\leqslant \dim R/P<n$
. The rest is easy.◻
$depth_{R}N\leqslant \dim R/P<n$
. The rest is easy.◻
Corollary 2.13. Let
![]() $n\geqslant 1$
, and
$n\geqslant 1$
, and
![]() $M$
and
$M$
and
![]() $N$
be finite
$N$
be finite
![]() $R$
-modules. Assume that
$R$
-modules. Assume that
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n})$
condition and
$(S_{n})$
condition and
![]() $N$
satisfies the
$N$
satisfies the
![]() $(S_{n}^{\prime })$
condition. If
$(S_{n}^{\prime })$
condition. If
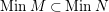 $MinM\subset MinN$
, then
$MinM\subset MinN$
, then
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{\prime })$
condition.
$(S_{n}^{\prime })$
condition.
Proof. Let
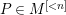 $P\in M^{[{<}n]}$
. As
$P\in M^{[{<}n]}$
. As
![]() $M$
satisfies
$M$
satisfies
![]() $(S_{n})$
,
$(S_{n})$
,
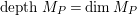 $depthM_{P}=\dim M_{P}$
. Take
$depthM_{P}=\dim M_{P}$
. Take
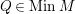 $Q\in MinM$
such that
$Q\in MinM$
such that
![]() $Q\subset P$
and
$Q\subset P$
and
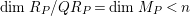 $\dim R_{P}/QR_{P}=\dim M_{P}<n$
. As
$\dim R_{P}/QR_{P}=\dim M_{P}<n$
. As
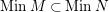 $MinM\subset MinN$
, we have that
$MinM\subset MinN$
, we have that
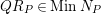 $QR_{P}\in MinN_{P}$
. By Lemma 2.12,
$QR_{P}\in MinN_{P}$
. By Lemma 2.12,
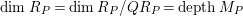 $\dim R_{P}=\dim R_{P}/QR_{P}= depthM_{P}$
, and hence
$\dim R_{P}=\dim R_{P}/QR_{P}= depthM_{P}$
, and hence
![]() $M$
satisfies
$M$
satisfies
![]() $(S_{n}^{\prime })$
.◻
$(S_{n}^{\prime })$
.◻
Corollary 2.14. Let
![]() $n\geqslant 1$
, and assume that
$n\geqslant 1$
, and assume that
![]() $R$
satisfies the
$R$
satisfies the
![]() $(S_{n})$
condition. Then for any finite
$(S_{n})$
condition. Then for any finite
![]() $R$
-module
$R$
-module
![]() $M$
,
$M$
,
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{\prime })$
condition if and only if
$(S_{n}^{\prime })$
condition if and only if
![]() $M$
satisfies both
$M$
satisfies both
![]() $(S_{n})$
and
$(S_{n})$
and
![]() $(S_{1}^{\prime })$
.
$(S_{1}^{\prime })$
.
Proof. Obviously, if
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{\prime })$
condition, then it satisfies both
$(S_{n}^{\prime })$
condition, then it satisfies both
![]() $(S_{n})$
and
$(S_{n})$
and
![]() $(S_{1}^{\prime })$
. For the converse, apply Corollary 2.13 for
$(S_{1}^{\prime })$
. For the converse, apply Corollary 2.13 for
![]() $N=R$
.◻
$N=R$
.◻
2.15
Let
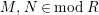 $M,N\in modR$
. We say that
$M,N\in modR$
. We say that
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{\prime })_{N}$
-condition, or
$(S_{n}^{\prime })_{N}$
-condition, or
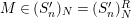 $M\in (S_{n}^{\prime })_{N}=(S_{n}^{\prime })_{N}^{R}$
, if
$M\in (S_{n}^{\prime })_{N}=(S_{n}^{\prime })_{N}^{R}$
, if
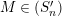 $M\in (S_{n}^{\prime })$
and
$M\in (S_{n}^{\prime })$
and
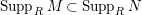 $Supp_{R}M\subset Supp_{R}N$
.
$Supp_{R}M\subset Supp_{R}N$
.
Lemma 2.16. Let
![]() $n\geqslant 1$
, and
$n\geqslant 1$
, and
![]() $M$
and
$M$
and
![]() $N$
be finite
$N$
be finite
![]() $R$
-modules. Assume that
$R$
-modules. Assume that
![]() $N$
satisfies
$N$
satisfies
![]() $(S_{n}^{\prime })$
. Then the following are equivalent.
$(S_{n}^{\prime })$
. Then the following are equivalent.
-
(1)
 $M$
satisfies
$M$
satisfies
 $(S_{n}^{\prime })_{N}$
.
$(S_{n}^{\prime })_{N}$
. -
(2)
 $M$
satisfies
$M$
satisfies
 $(S_{n})$
and
$(S_{n})$
and
 $MinM\subset MinN$
.
$MinM\subset MinN$
.
Proof. (1)
![]() $\Rightarrow$
(2). As
$\Rightarrow$
(2). As
![]() $(S_{n}^{\prime })$
implies
$(S_{n}^{\prime })$
implies
![]() $(S_{n})$
, we have that
$(S_{n})$
, we have that
![]() $M$
satisfies
$M$
satisfies
![]() $(S_{n})$
. As
$(S_{n})$
. As
![]() $M$
satisfies
$M$
satisfies
![]() $(S_{n}^{\prime })$
with
$(S_{n}^{\prime })$
with
![]() $n\geqslant 1$
, we have that
$n\geqslant 1$
, we have that
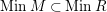 $MinM\subset MinR$
. By assumption,
$MinM\subset MinR$
. By assumption,
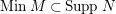 $MinM\subset SuppN$
. So
$MinM\subset SuppN$
. So
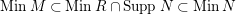 $MinM\subset MinR\cap SuppN\subset MinN$
.
$MinM\subset MinR\cap SuppN\subset MinN$
.
(2)
![]() $\Rightarrow$
(1).
$\Rightarrow$
(1).
![]() $M$
satisfies
$M$
satisfies
![]() $(S_{n}^{\prime })$
by Corollary 2.13.
$(S_{n}^{\prime })$
by Corollary 2.13.
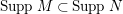 $SuppM\subset SuppN$
follows from
$SuppM\subset SuppN$
follows from
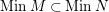 $MinM\subset MinN$
.◻
$MinM\subset MinN$
.◻
2.17
There is another case that
![]() $(S_{n})$
implies
$(S_{n})$
implies
![]() $(S_{n}^{\prime })$
. An
$(S_{n}^{\prime })$
. An
![]() $R$
-module
$R$
-module
![]() $N$
is said to be full if
$N$
is said to be full if
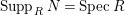 $Supp_{R}N= SpecR$
. A finitely generated faithful
$Supp_{R}N= SpecR$
. A finitely generated faithful
![]() $R$
-module is full.
$R$
-module is full.
Lemma 2.18. Let
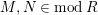 $M,N\in modR$
. If
$M,N\in modR$
. If
![]() $N$
is a full
$N$
is a full
![]() $R$
-module, then
$R$
-module, then
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{\prime })$
condition if and only if
$(S_{n}^{\prime })$
condition if and only if
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{N})$
condition. If
$(S_{n}^{N})$
condition. If
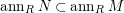 $ann_{R}N\subset ann_{R}M$
, then
$ann_{R}N\subset ann_{R}M$
, then
![]() $M$
satisfies the
$M$
satisfies the
![]() $(S_{n}^{N})^{R}$
condition if and only if
$(S_{n}^{N})^{R}$
condition if and only if
![]() $M$
satisfies the
$M$
satisfies the
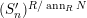 $(S_{n}^{\prime })^{R/ ann_{R}N}$
condition.
$(S_{n}^{\prime })^{R/ ann_{R}N}$
condition.
Proof. Left to the reader. ◻
Lemma 2.19. Let
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $R$
, and
$R$
, and
![]() $S$
a module-finite commutative
$S$
a module-finite commutative
![]() $R$
-algebra. For a finite
$R$
-algebra. For a finite
![]() $S$
-module
$S$
-module
![]() $M$
, we have that
$M$
, we have that
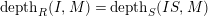 $depth_{R}(I,M)= depth_{S}(IS,M)$
. In particular, if
$depth_{R}(I,M)= depth_{S}(IS,M)$
. In particular, if
![]() $R$
is semilocal, then
$R$
is semilocal, then
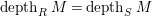 $depth_{R}M= depth_{S}M$
.
$depth_{R}M= depth_{S}M$
.
Proof. Note that
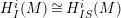 $H_{I}^{i}(M)\cong H_{IS}^{i}(M)$
by [Reference Brodmann and SharpBS, (4.2.1)]. By [Reference Brodmann and SharpBS, (6.2.7)], we get the lemma immediately.◻
$H_{I}^{i}(M)\cong H_{IS}^{i}(M)$
by [Reference Brodmann and SharpBS, (4.2.1)]. By [Reference Brodmann and SharpBS, (6.2.7)], we get the lemma immediately.◻
Lemma 2.20. Let
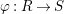 $\unicode[STIX]{x1D711}:R\rightarrow S$
be a finite homomorphism of rings,
$\unicode[STIX]{x1D711}:R\rightarrow S$
be a finite homomorphism of rings,
![]() $M$
a finite
$M$
a finite
![]() $S$
-module, and
$S$
-module, and
![]() $n\geqslant 0$
.
$n\geqslant 0$
.
-
(1) If
 $M$
satisfies
$M$
satisfies
 $(S_{n}^{\prime })$
as an
$(S_{n}^{\prime })$
as an
 $R$
-module, then it satisfies
$R$
-module, then it satisfies
 $(S_{n}^{\prime })$
as an
$(S_{n}^{\prime })$
as an
 $S$
-module.
$S$
-module. -
(2) Assume that for any
 $Q\in MinS$
,
$Q\in MinS$
,
 $\unicode[STIX]{x1D711}^{-1}(Q)\in MinR$
(e.g.,
$\unicode[STIX]{x1D711}^{-1}(Q)\in MinR$
(e.g.,
 $S$
satisfies
$S$
satisfies
 $(S_{1}^{\prime })$
as an
$(S_{1}^{\prime })$
as an
 $R$
-module). If
$R$
-module). If
 $M$
satisfies
$M$
satisfies
 $(S_{n}^{\prime })$
as an
$(S_{n}^{\prime })$
as an
 $S$
-module and
$S$
-module and
 $R_{P}$
is quasi-unmixed for any prime
$R_{P}$
is quasi-unmixed for any prime
 $P$
of
$P$
of
 $R$
with
$R$
with
 $depthR_{P}<n$
, then
$depthR_{P}<n$
, then
 $M$
satisfies
$M$
satisfies
 $(S_{n}^{\prime })$
as an
$(S_{n}^{\prime })$
as an
 $R$
-module.
$R$
-module.
Proof. We only prove (2). Let
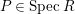 $P\in SpecR$
, and
$P\in SpecR$
, and
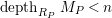 $depth_{R_{P}}M_{P}<n$
. Then by Lemma 2.19 and [Reference Brodmann and SharpBS, (6.2.7)], there exists some
$depth_{R_{P}}M_{P}<n$
. Then by Lemma 2.19 and [Reference Brodmann and SharpBS, (6.2.7)], there exists some
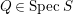 $Q\in SpecS$
such that
$Q\in SpecS$
such that
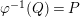 $\unicode[STIX]{x1D711}^{-1}(Q)=P$
and
$\unicode[STIX]{x1D711}^{-1}(Q)=P$
and
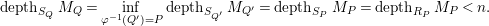 $$\begin{eqnarray}depth_{S_{Q}}M_{Q}=\inf _{\unicode[STIX]{x1D711}^{-1}(Q^{\prime })=P} depth_{S_{Q^{\prime }}}M_{Q^{\prime }}= depth_{S_{P}}M_{P}= depth_{R_{P}}M_{P}<n.\end{eqnarray}$$
$$\begin{eqnarray}depth_{S_{Q}}M_{Q}=\inf _{\unicode[STIX]{x1D711}^{-1}(Q^{\prime })=P} depth_{S_{Q^{\prime }}}M_{Q^{\prime }}= depth_{S_{P}}M_{P}= depth_{R_{P}}M_{P}<n.\end{eqnarray}$$
Then
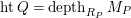 $htQ= depth_{R_{P}}M_{P}$
. So it suffices to show
$htQ= depth_{R_{P}}M_{P}$
. So it suffices to show
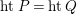 $htP= htQ$
. By assumption,
$htP= htQ$
. By assumption,
![]() $R_{P}$
is quasi-unmixed. So
$R_{P}$
is quasi-unmixed. So
![]() $R_{P}$
is equidimensional and universally catenary [Reference MatsumuraMat, (31.6)]. By [Reference GrothendieckGro, (13.3.6)],
$R_{P}$
is equidimensional and universally catenary [Reference MatsumuraMat, (31.6)]. By [Reference GrothendieckGro, (13.3.6)],
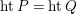 $htP= htQ$
, as desired.◻
$htP= htQ$
, as desired.◻
2.21
We say that
![]() $R$
satisfies
$R$
satisfies
![]() $(R_{n})$
(resp.
$(R_{n})$
(resp.
![]() $(T_{n})$
) if
$(T_{n})$
) if
![]() $R_{P}$
is regular (resp. Gorenstein) for any prime
$R_{P}$
is regular (resp. Gorenstein) for any prime
![]() $P$
of
$P$
of
![]() $R$
with
$R$
with
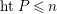 $htP\leqslant n$
.
$htP\leqslant n$
.
3
 ${\mathcal{X}}_{n,m}$
-approximation
${\mathcal{X}}_{n,m}$
-approximation
3.1
Let
![]() ${\mathcal{A}}$
be an abelian category, and
${\mathcal{A}}$
be an abelian category, and
![]() ${\mathcal{C}}$
its additive subcategory closed under direct summands. Let
${\mathcal{C}}$
its additive subcategory closed under direct summands. Let
![]() $n\geqslant 0$
. We define
$n\geqslant 0$
. We define
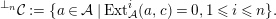 $$\begin{eqnarray}\text{}^{\bot _{n}}{\mathcal{C}}:=\{a\in {\mathcal{A}}\mid Ext_{{\mathcal{A}}}^{i}(a,c)=0,1\leqslant i\leqslant n\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{\bot _{n}}{\mathcal{C}}:=\{a\in {\mathcal{A}}\mid Ext_{{\mathcal{A}}}^{i}(a,c)=0,1\leqslant i\leqslant n\}.\end{eqnarray}$$
Let
![]() $a\in {\mathcal{A}}$
. A sequence
$a\in {\mathcal{A}}$
. A sequence
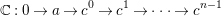 $$\begin{eqnarray}\mathbb{C}:0\rightarrow a\rightarrow c^{0}\rightarrow c^{1}\rightarrow \cdots \rightarrow c^{n-1}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}:0\rightarrow a\rightarrow c^{0}\rightarrow c^{1}\rightarrow \cdots \rightarrow c^{n-1}\end{eqnarray}$$
is said to be an
![]() $(n,{\mathcal{C}})$
-pushforward if it is exact with
$(n,{\mathcal{C}})$
-pushforward if it is exact with
![]() $c^{i}\in {\mathcal{C}}$
. If in addition,
$c^{i}\in {\mathcal{C}}$
. If in addition,
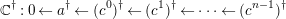 $$\begin{eqnarray}\mathbb{C}^{\dagger }:0\leftarrow a^{\dagger }\leftarrow (c^{0})^{\dagger }\leftarrow (c^{1})^{\dagger }\leftarrow \cdots \leftarrow (c^{n-1})^{\dagger }\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}^{\dagger }:0\leftarrow a^{\dagger }\leftarrow (c^{0})^{\dagger }\leftarrow (c^{1})^{\dagger }\leftarrow \cdots \leftarrow (c^{n-1})^{\dagger }\end{eqnarray}$$
is exact for any
![]() $c\in {\mathcal{C}}$
, where
$c\in {\mathcal{C}}$
, where
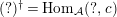 $(?)^{\dagger }= Hom_{{\mathcal{A}}}(?,c)$
, we say that
$(?)^{\dagger }= Hom_{{\mathcal{A}}}(?,c)$
, we say that
![]() $\mathbb{C}$
is a universal
$\mathbb{C}$
is a universal
![]() $(n,{\mathcal{C}})$
-pushforward.
$(n,{\mathcal{C}})$
-pushforward.
If
![]() $a\in {\mathcal{A}}$
has an
$a\in {\mathcal{A}}$
has an
![]() $(n,{\mathcal{C}})$
-pushforward, we say that
$(n,{\mathcal{C}})$
-pushforward, we say that
![]() $a$
is an
$a$
is an
![]() $(n,{\mathcal{C}})$
-syzygy, and we write
$(n,{\mathcal{C}})$
-syzygy, and we write
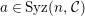 $a\in Syz(n,{\mathcal{C}})$
. If
$a\in Syz(n,{\mathcal{C}})$
. If
![]() $a\in {\mathcal{A}}$
has a universal
$a\in {\mathcal{A}}$
has a universal
![]() $(n,{\mathcal{C}})$
-pushforward, we say that
$(n,{\mathcal{C}})$
-pushforward, we say that
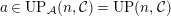 $a\in UP_{{\mathcal{A}}}(n,{\mathcal{C}})= UP(n,{\mathcal{C}})$
. Obviously,
$a\in UP_{{\mathcal{A}}}(n,{\mathcal{C}})= UP(n,{\mathcal{C}})$
. Obviously,
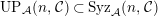 $UP_{{\mathcal{A}}}(n,{\mathcal{C}})\subset Syz_{{\mathcal{A}}}(n,{\mathcal{C}})$
.
$UP_{{\mathcal{A}}}(n,{\mathcal{C}})\subset Syz_{{\mathcal{A}}}(n,{\mathcal{C}})$
.
3.2
We write
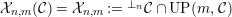 ${\mathcal{X}}_{n,m}({\mathcal{C}})={\mathcal{X}}_{n,m}:=\text{}^{\bot _{n}}{\mathcal{C}}\cap UP(m,{\mathcal{C}})$
for
${\mathcal{X}}_{n,m}({\mathcal{C}})={\mathcal{X}}_{n,m}:=\text{}^{\bot _{n}}{\mathcal{C}}\cap UP(m,{\mathcal{C}})$
for
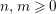 $n,m\geqslant 0$
. Also, for
$n,m\geqslant 0$
. Also, for
![]() $a\neq 0$
, we define
$a\neq 0$
, we define
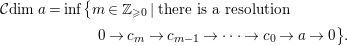 $$\begin{eqnarray}\displaystyle & {\mathcal{C}}dima=\inf \!\big\{m\in \mathbb{Z}_{{\geqslant}0}\mid \text{there is a resolution } & \displaystyle \nonumber\\ \displaystyle & \qquad \qquad \qquad \qquad \qquad 0\rightarrow c_{m}\rightarrow c_{m-1}\rightarrow \cdots \rightarrow c_{0}\rightarrow a\rightarrow 0\big\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\mathcal{C}}dima=\inf \!\big\{m\in \mathbb{Z}_{{\geqslant}0}\mid \text{there is a resolution } & \displaystyle \nonumber\\ \displaystyle & \qquad \qquad \qquad \qquad \qquad 0\rightarrow c_{m}\rightarrow c_{m-1}\rightarrow \cdots \rightarrow c_{0}\rightarrow a\rightarrow 0\big\}. & \displaystyle \nonumber\end{eqnarray}$$
We define
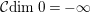 ${\mathcal{C}}dim\,0=-\infty$
. We define
${\mathcal{C}}dim\,0=-\infty$
. We define
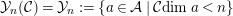 ${\mathcal{Y}}_{n}({\mathcal{C}})={\mathcal{Y}}_{n}:=\{a\in {\mathcal{A}}\mid {\mathcal{C}}dim\,a<n\}$
. A sequence
${\mathcal{Y}}_{n}({\mathcal{C}})={\mathcal{Y}}_{n}:=\{a\in {\mathcal{A}}\mid {\mathcal{C}}dim\,a<n\}$
. A sequence
![]() $\mathbb{E}$
is said to be
$\mathbb{E}$
is said to be
![]() ${\mathcal{C}}$
-exact if it is exact, and
${\mathcal{C}}$
-exact if it is exact, and
![]() ${\mathcal{A}}(\mathbb{E},c)$
is also exact for each
${\mathcal{A}}(\mathbb{E},c)$
is also exact for each
![]() $c\in {\mathcal{C}}$
. Letting a
$c\in {\mathcal{C}}$
. Letting a
![]() ${\mathcal{C}}$
-exact sequence an exact sequence,
${\mathcal{C}}$
-exact sequence an exact sequence,
![]() ${\mathcal{A}}$
is an exact category, which we denote by
${\mathcal{A}}$
is an exact category, which we denote by
![]() ${\mathcal{A}}_{{\mathcal{C}}}$
in order to distinguish it from the abelian category
${\mathcal{A}}_{{\mathcal{C}}}$
in order to distinguish it from the abelian category
![]() ${\mathcal{A}}$
(with the usual exact sequences).
${\mathcal{A}}$
(with the usual exact sequences).
3.3
Let
![]() ${\mathcal{C}}_{0}\subset {\mathcal{A}}$
be a subset. Then
${\mathcal{C}}_{0}\subset {\mathcal{A}}$
be a subset. Then
![]() $\text{}^{\bot _{n}}{\mathcal{C}}_{0}$
,
$\text{}^{\bot _{n}}{\mathcal{C}}_{0}$
,
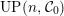 $UP(n,{\mathcal{C}}_{0})$
,
$UP(n,{\mathcal{C}}_{0})$
,
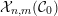 ${\mathcal{X}}_{n,m}({\mathcal{C}}_{0})$
,
${\mathcal{X}}_{n,m}({\mathcal{C}}_{0})$
,
![]() $\{$
, and
$\{$
, and
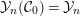 ${\mathcal{Y}}_{n}({\mathcal{C}}_{0})={\mathcal{Y}}_{n}$
mean
${\mathcal{Y}}_{n}({\mathcal{C}}_{0})={\mathcal{Y}}_{n}$
mean
![]() $\text{}^{\bot _{n}}{\mathcal{C}}$
,
$\text{}^{\bot _{n}}{\mathcal{C}}$
,
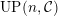 $UP(n,{\mathcal{C}})$
,
$UP(n,{\mathcal{C}})$
,
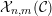 ${\mathcal{X}}_{n,m}({\mathcal{C}})$
,
${\mathcal{X}}_{n,m}({\mathcal{C}})$
,
![]() ${\mathcal{C}}dim$
, and
${\mathcal{C}}dim$
, and
![]() ${\mathcal{Y}}_{n}({\mathcal{C}})$
, respectively, where
${\mathcal{Y}}_{n}({\mathcal{C}})$
, respectively, where
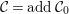 ${\mathcal{C}}= add{\mathcal{C}}_{0}$
, the smallest additive subcategory containing
${\mathcal{C}}= add{\mathcal{C}}_{0}$
, the smallest additive subcategory containing
![]() ${\mathcal{C}}_{0}$
and closed under direct summands. A
${\mathcal{C}}_{0}$
and closed under direct summands. A
![]() ${\mathcal{C}}_{0}$
-exact sequence means a
${\mathcal{C}}_{0}$
-exact sequence means a
![]() ${\mathcal{C}}$
-exact sequence. A sequence
${\mathcal{C}}$
-exact sequence. A sequence
![]() $\mathbb{E}$
in
$\mathbb{E}$
in
![]() ${\mathcal{A}}$
is
${\mathcal{A}}$
is
![]() ${\mathcal{C}}_{0}$
-exact if and only if it is exact, and for any
${\mathcal{C}}_{0}$
-exact if and only if it is exact, and for any
![]() $c\in {\mathcal{C}}_{0}$
,
$c\in {\mathcal{C}}_{0}$
,
![]() ${\mathcal{A}}(\mathbb{E},c)$
is exact. If
${\mathcal{A}}(\mathbb{E},c)$
is exact. If
![]() $c\in {\mathcal{A}}$
,
$c\in {\mathcal{A}}$
,
![]() $\text{}^{\bot _{n}}c$
,
$\text{}^{\bot _{n}}c$
,
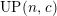 $UP(n,c)$
and so on mean
$UP(n,c)$
and so on mean
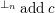 $\text{}^{\bot _{n}} addc$
,
$\text{}^{\bot _{n}} addc$
,
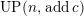 $UP(n,addc)$
and so on.
$UP(n,addc)$
and so on.
3.4
By definition, any object of
![]() ${\mathcal{C}}$
is an injective object in
${\mathcal{C}}$
is an injective object in
![]() ${\mathcal{A}}_{{\mathcal{C}}}$
.
${\mathcal{A}}_{{\mathcal{C}}}$
.
3.5
Let
![]() ${\mathcal{E}}$
be an exact category, and
${\mathcal{E}}$
be an exact category, and
![]() ${\mathcal{I}}$
an additive subcategory of
${\mathcal{I}}$
an additive subcategory of
![]() ${\mathcal{E}}$
. Then for
${\mathcal{E}}$
. Then for
![]() $e\in {\mathcal{E}}$
, we define
$e\in {\mathcal{E}}$
, we define
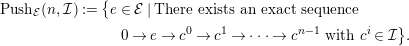 $$\begin{eqnarray}\displaystyle & & \displaystyle Push_{{\mathcal{E}}}(n,{\mathcal{I}}):=\big\{e\in {\mathcal{E}}\mid \text{There exists an exact sequence}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \qquad \qquad 0\rightarrow e\rightarrow c^{0}\rightarrow c^{1}\rightarrow \cdots \rightarrow c^{n-1}\text{ with }c^{i}\in {\mathcal{I}}\big\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle Push_{{\mathcal{E}}}(n,{\mathcal{I}}):=\big\{e\in {\mathcal{E}}\mid \text{There exists an exact sequence}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \qquad \qquad 0\rightarrow e\rightarrow c^{0}\rightarrow c^{1}\rightarrow \cdots \rightarrow c^{n-1}\text{ with }c^{i}\in {\mathcal{I}}\big\}.\nonumber\end{eqnarray}$$
Note that
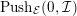 $Push_{{\mathcal{E}}}(0,{\mathcal{I}})$
is the whole
$Push_{{\mathcal{E}}}(0,{\mathcal{I}})$
is the whole
![]() ${\mathcal{E}}$
. Thus
${\mathcal{E}}$
. Thus
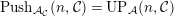 $Push_{{\mathcal{A}}_{{\mathcal{C}}}}(n,{\mathcal{C}})= UP_{{\mathcal{A}}}(n,{\mathcal{C}})$
.
$Push_{{\mathcal{A}}_{{\mathcal{C}}}}(n,{\mathcal{C}})= UP_{{\mathcal{A}}}(n,{\mathcal{C}})$
.
If
![]() $a\in {\mathcal{E}}$
is a direct summand of an object of
$a\in {\mathcal{E}}$
is a direct summand of an object of
![]() ${\mathcal{I}}$
, then
${\mathcal{I}}$
, then
![]() $a$
admits an exact sequence
$a$
admits an exact sequence
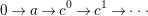 $$\begin{eqnarray}0\rightarrow a\rightarrow c^{0}\rightarrow c^{1}\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow a\rightarrow c^{0}\rightarrow c^{1}\rightarrow \cdots\end{eqnarray}$$
with
![]() $c^{i}\in {\mathcal{I}}$
, and hence
$c^{i}\in {\mathcal{I}}$
, and hence
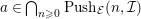 $a\in \bigcap _{n\geqslant 0} Push_{{\mathcal{E}}}(n,{\mathcal{I}})$
.
$a\in \bigcap _{n\geqslant 0} Push_{{\mathcal{E}}}(n,{\mathcal{I}})$
.
Lemma 3.6. Let
![]() ${\mathcal{E}}$
be an exact category. Let
${\mathcal{E}}$
be an exact category. Let
![]() ${\mathcal{I}}$
be an additive subcategory of
${\mathcal{I}}$
be an additive subcategory of
![]() ${\mathcal{E}}$
consisting of injective objects. Let
${\mathcal{E}}$
consisting of injective objects. Let
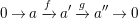 $$\begin{eqnarray}0\rightarrow a\xrightarrow[{}]{f}a^{\prime }\xrightarrow[{}]{g}a^{\prime \prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow a\xrightarrow[{}]{f}a^{\prime }\xrightarrow[{}]{g}a^{\prime \prime }\rightarrow 0\end{eqnarray}$$
be an exact sequence in
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() $m\geqslant 0$
. Then
$m\geqslant 0$
. Then
-
(1) If
 $a\in Push(m,{\mathcal{I}})$
and
$a\in Push(m,{\mathcal{I}})$
and
 $a^{\prime \prime }\in Push(m,{\mathcal{I}})$
, then
$a^{\prime \prime }\in Push(m,{\mathcal{I}})$
, then
 $a^{\prime }\in Push(m,{\mathcal{I}})$
.
$a^{\prime }\in Push(m,{\mathcal{I}})$
. -
(2) If
 $a^{\prime }\in Push(m+1,{\mathcal{I}})$
and
$a^{\prime }\in Push(m+1,{\mathcal{I}})$
and
 $a^{\prime \prime }\in Push(m,{\mathcal{I}})$
, then
$a^{\prime \prime }\in Push(m,{\mathcal{I}})$
, then
 $a\in Push(m+1,{\mathcal{I}})$
.
$a\in Push(m+1,{\mathcal{I}})$
. -
(3) If
 $a\in Push(m+1,{\mathcal{I}})$
,
$a\in Push(m+1,{\mathcal{I}})$
,
 $a^{\prime }\in Push(m,{\mathcal{I}})$
, then
$a^{\prime }\in Push(m,{\mathcal{I}})$
, then
 $a^{\prime \prime }\in Push(m,{\mathcal{I}})$
.
$a^{\prime \prime }\in Push(m,{\mathcal{I}})$
.
Proof. Let
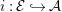 $i:{\mathcal{E}}{\hookrightarrow}{\mathcal{A}}$
be the Gabriel–Quillen embedding [Reference Thomason and TrobaughTT]. We consider that
$i:{\mathcal{E}}{\hookrightarrow}{\mathcal{A}}$
be the Gabriel–Quillen embedding [Reference Thomason and TrobaughTT]. We consider that
![]() ${\mathcal{E}}$
is a full subcategory of
${\mathcal{E}}$
is a full subcategory of
![]() ${\mathcal{A}}$
closed under extensions, and a sequence in
${\mathcal{A}}$
closed under extensions, and a sequence in
![]() ${\mathcal{E}}$
is exact if and only if it is so in
${\mathcal{E}}$
is exact if and only if it is so in
![]() ${\mathcal{A}}$
.
${\mathcal{A}}$
.
We prove (1). We use induction on
![]() $m$
. The case that
$m$
. The case that
![]() $m=0$
is trivial, and so we assume that
$m=0$
is trivial, and so we assume that
![]() $m>0$
. Let
$m>0$
. Let
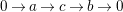 $$\begin{eqnarray}0\rightarrow a\rightarrow c\rightarrow b\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow a\rightarrow c\rightarrow b\rightarrow 0\end{eqnarray}$$
be an exact sequence such that
![]() $c\in {\mathcal{I}}$
and
$c\in {\mathcal{I}}$
and
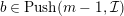 $b\in Push(m-1,{\mathcal{I}})$
. Let
$b\in Push(m-1,{\mathcal{I}})$
. Let
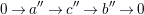 $$\begin{eqnarray}0\rightarrow a^{\prime \prime }\rightarrow c^{\prime \prime }\rightarrow b^{\prime \prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow a^{\prime \prime }\rightarrow c^{\prime \prime }\rightarrow b^{\prime \prime }\rightarrow 0\end{eqnarray}$$
be an exact sequence such that
![]() $c^{\prime \prime }\in {\mathcal{I}}$
and
$c^{\prime \prime }\in {\mathcal{I}}$
and
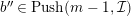 $b^{\prime \prime }\in Push(m-1,{\mathcal{I}})$
. As
$b^{\prime \prime }\in Push(m-1,{\mathcal{I}})$
. As
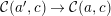 ${\mathcal{C}}(a^{\prime },c)\rightarrow {\mathcal{C}}(a,c)$
is surjective, we can form a commutative diagram with exact rows and columns
${\mathcal{C}}(a^{\prime },c)\rightarrow {\mathcal{C}}(a,c)$
is surjective, we can form a commutative diagram with exact rows and columns
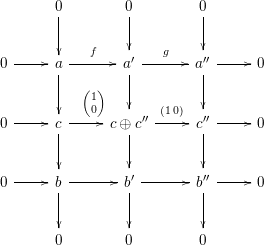
in
![]() ${\mathcal{A}}$
. As
${\mathcal{A}}$
. As
![]() ${\mathcal{E}}$
is closed under extensions in
${\mathcal{E}}$
is closed under extensions in
![]() ${\mathcal{A}}$
, this diagram is a diagram in
${\mathcal{A}}$
, this diagram is a diagram in
![]() ${\mathcal{E}}$
. By induction hypothesis,
${\mathcal{E}}$
. By induction hypothesis,
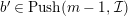 $b^{\prime }\in Push(m-1,{\mathcal{I}})$
. Hence
$b^{\prime }\in Push(m-1,{\mathcal{I}})$
. Hence
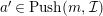 $a^{\prime }\in Push(m,{\mathcal{I}})$
.
$a^{\prime }\in Push(m,{\mathcal{I}})$
.
We prove (2). Let
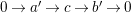 $0\rightarrow a^{\prime }\rightarrow c\rightarrow b^{\prime }\rightarrow 0$
be an exact sequence in
$0\rightarrow a^{\prime }\rightarrow c\rightarrow b^{\prime }\rightarrow 0$
be an exact sequence in
![]() ${\mathcal{E}}$
such that
${\mathcal{E}}$
such that
![]() $c\in {\mathcal{I}}$
and
$c\in {\mathcal{I}}$
and
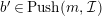 $b^{\prime }\in Push(m,{\mathcal{I}})$
. Then we have a commutative diagram in
$b^{\prime }\in Push(m,{\mathcal{I}})$
. Then we have a commutative diagram in
![]() ${\mathcal{E}}$
with exact rows and columns
${\mathcal{E}}$
with exact rows and columns
Applying (1), which we have already proved,
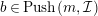 $b\in Push(m,{\mathcal{I}})$
, since
$b\in Push(m,{\mathcal{I}})$
, since
![]() $a^{\prime \prime }$
and
$a^{\prime \prime }$
and
![]() $b^{\prime }$
lie in
$b^{\prime }$
lie in
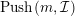 $Push(m,{\mathcal{I}})$
. So
$Push(m,{\mathcal{I}})$
. So
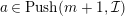 $a\in Push(m+1,{\mathcal{I}})$
, as desired.
$a\in Push(m+1,{\mathcal{I}})$
, as desired.
We prove (3). Let
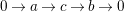 $0\rightarrow a\rightarrow c\rightarrow b\rightarrow 0$
be an exact sequence in
$0\rightarrow a\rightarrow c\rightarrow b\rightarrow 0$
be an exact sequence in
![]() ${\mathcal{E}}$
such that
${\mathcal{E}}$
such that
![]() $c\in {\mathcal{I}}$
and
$c\in {\mathcal{I}}$
and
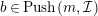 $b\in Push(m,{\mathcal{I}})$
. Take the push-out diagram
$b\in Push(m,{\mathcal{I}})$
. Take the push-out diagram
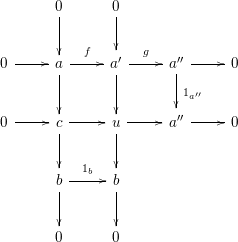
Then
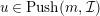 $u\in Push(m,{\mathcal{I}})$
by (1), which we have already proved. Since
$u\in Push(m,{\mathcal{I}})$
by (1), which we have already proved. Since
![]() $c\in {\mathcal{I}}$
, the middle row splits. Then by the exact sequence
$c\in {\mathcal{I}}$
, the middle row splits. Then by the exact sequence
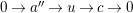 $0\rightarrow a^{\prime \prime }\rightarrow u\rightarrow c\rightarrow 0$
and (2), we have that
$0\rightarrow a^{\prime \prime }\rightarrow u\rightarrow c\rightarrow 0$
and (2), we have that
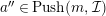 $a^{\prime \prime }\in Push(m,{\mathcal{I}})$
, as desired.◻
$a^{\prime \prime }\in Push(m,{\mathcal{I}})$
, as desired.◻
Corollary 3.7. Let
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() ${\mathcal{I}}$
be as in Lemma 3.6. Let
${\mathcal{I}}$
be as in Lemma 3.6. Let
![]() $m\geqslant 0$
, and
$m\geqslant 0$
, and
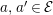 $a,a^{\prime }\in {\mathcal{E}}$
. Then
$a,a^{\prime }\in {\mathcal{E}}$
. Then
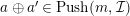 $a\oplus a^{\prime }\in Push(m,{\mathcal{I}})$
if and only if
$a\oplus a^{\prime }\in Push(m,{\mathcal{I}})$
if and only if
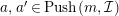 $a,a^{\prime }\in Push(m,{\mathcal{I}})$
.
$a,a^{\prime }\in Push(m,{\mathcal{I}})$
.
Proof. The ‘if’ part is obvious by Lemma 3.6(1), considering the exact sequence
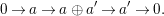 $$\begin{eqnarray}0\rightarrow a\rightarrow a\oplus a^{\prime }\rightarrow a^{\prime }\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow a\rightarrow a\oplus a^{\prime }\rightarrow a^{\prime }\rightarrow 0.\end{eqnarray}$$
We prove the ‘only if’ part by induction on
![]() $m$
. If
$m$
. If
![]() $m=0$
, then there is nothing to prove. Let
$m=0$
, then there is nothing to prove. Let
![]() $m>0$
. Then by induction hypothesis,
$m>0$
. Then by induction hypothesis,
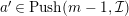 $a^{\prime }\in Push(m-1,{\mathcal{I}})$
. Then applying Lemma 3.6(2) to the exact sequence (2), we have that
$a^{\prime }\in Push(m-1,{\mathcal{I}})$
. Then applying Lemma 3.6(2) to the exact sequence (2), we have that
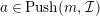 $a\in Push(m,{\mathcal{I}})$
.
$a\in Push(m,{\mathcal{I}})$
.
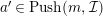 $a^{\prime }\in Push(m,{\mathcal{I}})$
is proved similarly.◻
$a^{\prime }\in Push(m,{\mathcal{I}})$
is proved similarly.◻
Corollary 3.8. Let
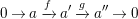 $$\begin{eqnarray}0\rightarrow a\xrightarrow[{}]{f}a^{\prime }\xrightarrow[{}]{g}a^{\prime \prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow a\xrightarrow[{}]{f}a^{\prime }\xrightarrow[{}]{g}a^{\prime \prime }\rightarrow 0\end{eqnarray}$$
be a
![]() ${\mathcal{C}}$
-exact sequence in
${\mathcal{C}}$
-exact sequence in
![]() ${\mathcal{A}}$
and
${\mathcal{A}}$
and
![]() $m\geqslant 0$
. Then
$m\geqslant 0$
. Then
-
(1) If
 $a\in UP(m,{\mathcal{C}})$
and
$a\in UP(m,{\mathcal{C}})$
and
 $a^{\prime \prime }\in UP(m,{\mathcal{C}})$
, then
$a^{\prime \prime }\in UP(m,{\mathcal{C}})$
, then
 $a^{\prime }\in UP(m,{\mathcal{C}})$
.
$a^{\prime }\in UP(m,{\mathcal{C}})$
. -
(2) If
 $a^{\prime }\in UP(m+1,{\mathcal{C}})$
and
$a^{\prime }\in UP(m+1,{\mathcal{C}})$
and
 $a^{\prime \prime }\in UP(m,{\mathcal{C}})$
, then
$a^{\prime \prime }\in UP(m,{\mathcal{C}})$
, then
 $a\in UP(m+1,{\mathcal{C}})$
.
$a\in UP(m+1,{\mathcal{C}})$
. -
(3) If
 $a\in UP(m+1,{\mathcal{C}})$
,
$a\in UP(m+1,{\mathcal{C}})$
,
 $a^{\prime }\in UP(m,{\mathcal{C}})$
, then
$a^{\prime }\in UP(m,{\mathcal{C}})$
, then
 $a^{\prime \prime }\in UP(m,{\mathcal{C}})$
.
$a^{\prime \prime }\in UP(m,{\mathcal{C}})$
.
3.9
We define
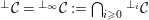 $\text{}^{\bot _{}}{\mathcal{C}}=\text{}^{\bot _{\infty }}{\mathcal{C}}:=\bigcap _{i\geqslant 0}\text{}^{\bot _{i}}{\mathcal{C}}$
and
$\text{}^{\bot _{}}{\mathcal{C}}=\text{}^{\bot _{\infty }}{\mathcal{C}}:=\bigcap _{i\geqslant 0}\text{}^{\bot _{i}}{\mathcal{C}}$
and
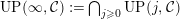 $UP(\infty ,{\mathcal{C}}):=\bigcap _{j\geqslant 0} UP(j,{\mathcal{C}})$
. Obviously,
$UP(\infty ,{\mathcal{C}}):=\bigcap _{j\geqslant 0} UP(j,{\mathcal{C}})$
. Obviously,
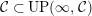 ${\mathcal{C}}\subset UP(\infty ,{\mathcal{C}})$
.
${\mathcal{C}}\subset UP(\infty ,{\mathcal{C}})$
.
Lemma 3.10. We have
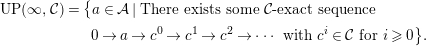 $$\begin{eqnarray}\displaystyle & & \displaystyle UP(\infty ,{\mathcal{C}})=\big\{a\in {\mathcal{A}}\mid \text{There exists some }{\mathcal{C}}\text{-exact sequence }\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \qquad 0\rightarrow a\rightarrow c^{0}\rightarrow c^{1}\rightarrow c^{2}\rightarrow \cdots \text{ with }c^{i}\in {\mathcal{C}}\text{for }i\geqslant 0\big\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle UP(\infty ,{\mathcal{C}})=\big\{a\in {\mathcal{A}}\mid \text{There exists some }{\mathcal{C}}\text{-exact sequence }\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \qquad 0\rightarrow a\rightarrow c^{0}\rightarrow c^{1}\rightarrow c^{2}\rightarrow \cdots \text{ with }c^{i}\in {\mathcal{C}}\text{for }i\geqslant 0\big\}.\nonumber\end{eqnarray}$$
Proof. Let
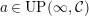 $a\in UP(\infty ,{\mathcal{C}})$
, and take any
$a\in UP(\infty ,{\mathcal{C}})$
, and take any
![]() ${\mathcal{C}}$
-exact sequence
${\mathcal{C}}$
-exact sequence
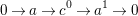 $$\begin{eqnarray}0\rightarrow a\rightarrow c^{0}\rightarrow a^{1}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow a\rightarrow c^{0}\rightarrow a^{1}\rightarrow 0\end{eqnarray}$$
with
![]() $c^{0}\in {\mathcal{C}}$
. Then
$c^{0}\in {\mathcal{C}}$
. Then
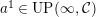 $a^{1}\in UP(\infty ,{\mathcal{C}})$
by Corollary 3.8, and we can continue infinitely.◻
$a^{1}\in UP(\infty ,{\mathcal{C}})$
by Corollary 3.8, and we can continue infinitely.◻
3.11
We define
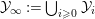 ${\mathcal{Y}}_{\infty }:=\bigcup _{i\geqslant 0}{\mathcal{Y}}_{i}$
. So
${\mathcal{Y}}_{\infty }:=\bigcup _{i\geqslant 0}{\mathcal{Y}}_{i}$
. So
![]() $a\in {\mathcal{Y}}_{\infty }$
if and only if
$a\in {\mathcal{Y}}_{\infty }$
if and only if
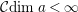 ${\mathcal{C}}dim\,a<\infty$
. We also define
${\mathcal{C}}dim\,a<\infty$
. We also define
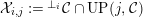 ${\mathcal{X}}_{i,j}:=\text{}^{\bot _{i}}{\mathcal{C}}\cap UP(j,{\mathcal{C}})$
for
${\mathcal{X}}_{i,j}:=\text{}^{\bot _{i}}{\mathcal{C}}\cap UP(j,{\mathcal{C}})$
for
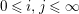 $0\leqslant i,j\leqslant \infty$
.
$0\leqslant i,j\leqslant \infty$
.
3.12
Let
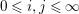 $0\leqslant i,j\leqslant \infty$
. We say that
$0\leqslant i,j\leqslant \infty$
. We say that
![]() $a\in {\mathcal{A}}$
lies in
$a\in {\mathcal{A}}$
lies in
![]() ${\mathcal{Z}}_{i,j}$
if there is a short exact sequence
${\mathcal{Z}}_{i,j}$
if there is a short exact sequence
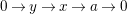 $$\begin{eqnarray}0\rightarrow y\rightarrow x\rightarrow a\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow y\rightarrow x\rightarrow a\rightarrow 0\end{eqnarray}$$
in
![]() ${\mathcal{A}}$
such that
${\mathcal{A}}$
such that
![]() $x\in {\mathcal{X}}_{i,j}$
and
$x\in {\mathcal{X}}_{i,j}$
and
![]() $y\in {\mathcal{Y}}_{i}$
.
$y\in {\mathcal{Y}}_{i}$
.
3.13
We define
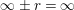 $\infty \pm r=\infty$
for
$\infty \pm r=\infty$
for
![]() $r\in \mathbb{R}$
.
$r\in \mathbb{R}$
.
Lemma 3.14. Let
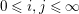 $0\leqslant i,j\leqslant \infty$
with
$0\leqslant i,j\leqslant \infty$
with
![]() $j\geqslant 1$
. Assume that
$j\geqslant 1$
. Assume that
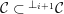 ${\mathcal{C}}\subset \text{}^{\bot _{i+1}}{\mathcal{C}}$
(that is,
${\mathcal{C}}\subset \text{}^{\bot _{i+1}}{\mathcal{C}}$
(that is,
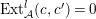 $Ext_{{\mathcal{A}}}^{l}(c,c^{\prime })=0$
for
$Ext_{{\mathcal{A}}}^{l}(c,c^{\prime })=0$
for
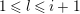 $1\leqslant l\leqslant i+1$
and
$1\leqslant l\leqslant i+1$
and
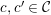 $c,c^{\prime }\in {\mathcal{C}}$
). Let
$c,c^{\prime }\in {\mathcal{C}}$
). Let
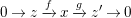 $0\rightarrow z\xrightarrow[{}]{f}x\xrightarrow[{}]{g}z^{\prime }\rightarrow 0$
be a short exact sequence in
$0\rightarrow z\xrightarrow[{}]{f}x\xrightarrow[{}]{g}z^{\prime }\rightarrow 0$
be a short exact sequence in
![]() ${\mathcal{A}}$
with
${\mathcal{A}}$
with
![]() $z\in {\mathcal{Z}}_{i,j}$
and
$z\in {\mathcal{Z}}_{i,j}$
and
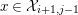 $x\in {\mathcal{X}}_{i+1,j-1}$
. Then
$x\in {\mathcal{X}}_{i+1,j-1}$
. Then
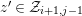 $z^{\prime }\in {\mathcal{Z}}_{i+1,j-1}$
.
$z^{\prime }\in {\mathcal{Z}}_{i+1,j-1}$
.
Proof. By assumption, there is an exact sequence
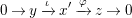 $$\begin{eqnarray}0\rightarrow y\xrightarrow[{}]{\unicode[STIX]{x1D704}}x^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D711}}z\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow y\xrightarrow[{}]{\unicode[STIX]{x1D704}}x^{\prime }\xrightarrow[{}]{\unicode[STIX]{x1D711}}z\rightarrow 0\end{eqnarray}$$
such that
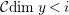 ${\mathcal{C}}dim\,y<i$
and
${\mathcal{C}}dim\,y<i$
and
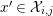 $x^{\prime }\in {\mathcal{X}}_{i,j}$
. As
$x^{\prime }\in {\mathcal{X}}_{i,j}$
. As
![]() $j\geqslant 1$
, there is an
$j\geqslant 1$
, there is an
![]() ${\mathcal{C}}$
-exact sequence
${\mathcal{C}}$
-exact sequence
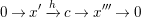 $$\begin{eqnarray}0\rightarrow x^{\prime }\xrightarrow[{}]{h}c\rightarrow x^{\prime \prime \prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow x^{\prime }\xrightarrow[{}]{h}c\rightarrow x^{\prime \prime \prime }\rightarrow 0\end{eqnarray}$$
such that
![]() $c\in {\mathcal{C}}$
. Then we have a commutative diagram with exact rows and columns
$c\in {\mathcal{C}}$
. Then we have a commutative diagram with exact rows and columns
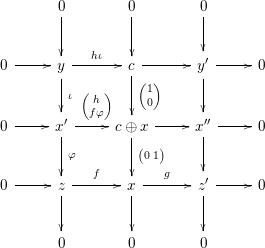
As the top row is exact,
![]() $y\in {\mathcal{Y}}_{i}$
, and
$y\in {\mathcal{Y}}_{i}$
, and
![]() $c\in {\mathcal{C}}$
,
$c\in {\mathcal{C}}$
,
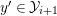 $y^{\prime }\in {\mathcal{Y}}_{i+1}$
. By assumption,
$y^{\prime }\in {\mathcal{Y}}_{i+1}$
. By assumption,
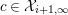 $c\in {\mathcal{X}}_{i+1,\infty }$
and
$c\in {\mathcal{X}}_{i+1,\infty }$
and
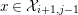 $x\in {\mathcal{X}}_{i+1,j-1}$
. So
$x\in {\mathcal{X}}_{i+1,j-1}$
. So
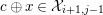 $c\oplus x\in {\mathcal{X}}_{i+1,j-1}$
. As the middle row is
$c\oplus x\in {\mathcal{X}}_{i+1,j-1}$
. As the middle row is
![]() ${\mathcal{C}}$
-exact and
${\mathcal{C}}$
-exact and
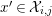 $x^{\prime }\in {\mathcal{X}}_{i,j}$
, we have that
$x^{\prime }\in {\mathcal{X}}_{i,j}$
, we have that
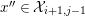 $x^{\prime \prime }\in {\mathcal{X}}_{i+1,j-1}$
by Corollary 3.8. The right column shows that
$x^{\prime \prime }\in {\mathcal{X}}_{i+1,j-1}$
by Corollary 3.8. The right column shows that
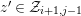 $z^{\prime }\in {\mathcal{Z}}_{i+1,j-1}$
, as desired.◻
$z^{\prime }\in {\mathcal{Z}}_{i+1,j-1}$
, as desired.◻
Lemma 3.15. Let
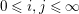 $0\leqslant i,j\leqslant \infty$
, and assume that
$0\leqslant i,j\leqslant \infty$
, and assume that
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
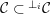 ${\mathcal{C}}\subset \text{}^{\bot _{i}}{\mathcal{C}}$
. Let
${\mathcal{C}}\subset \text{}^{\bot _{i}}{\mathcal{C}}$
. Let
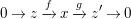 $$\begin{eqnarray}0\rightarrow z\xrightarrow[{}]{f}x\xrightarrow[{}]{g}z^{\prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow z\xrightarrow[{}]{f}x\xrightarrow[{}]{g}z^{\prime }\rightarrow 0\end{eqnarray}$$
be a short exact sequence in
![]() ${\mathcal{A}}$
with
${\mathcal{A}}$
with
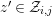 $z^{\prime }\in {\mathcal{Z}}_{i,j}$
and
$z^{\prime }\in {\mathcal{Z}}_{i,j}$
and
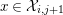 $x\in {\mathcal{X}}_{i,j+1}$
. Then
$x\in {\mathcal{X}}_{i,j+1}$
. Then
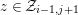 $z\in {\mathcal{Z}}_{i-1,j+1}$
.
$z\in {\mathcal{Z}}_{i-1,j+1}$
.
Proof. Take an exact sequence
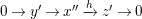 $0\rightarrow y^{\prime }\rightarrow x^{\prime \prime }\xrightarrow[{}]{h}z^{\prime }\rightarrow 0$
such that
$0\rightarrow y^{\prime }\rightarrow x^{\prime \prime }\xrightarrow[{}]{h}z^{\prime }\rightarrow 0$
such that
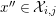 $x^{\prime \prime }\in {\mathcal{X}}_{i,j}$
and
$x^{\prime \prime }\in {\mathcal{X}}_{i,j}$
and
![]() $y^{\prime }\in {\mathcal{Y}}_{i}$
. Taking the pull-back of (3) by
$y^{\prime }\in {\mathcal{Y}}_{i}$
. Taking the pull-back of (3) by
![]() $h$
, we get a commutative diagram with exact rows and columns
$h$
, we get a commutative diagram with exact rows and columns
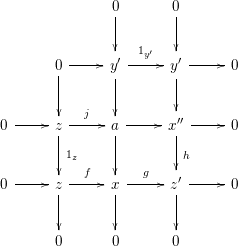
By induction, we can prove easily that
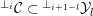 $\text{}^{\bot _{i}}{\mathcal{C}}\subset \text{}^{\bot _{i+1-l}}{\mathcal{Y}}_{l}$
. In particular,
$\text{}^{\bot _{i}}{\mathcal{C}}\subset \text{}^{\bot _{i+1-l}}{\mathcal{Y}}_{l}$
. In particular,
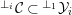 $\text{}^{\bot _{i}}{\mathcal{C}}\subset \text{}^{\bot _{1}}{\mathcal{Y}}_{i}$
, and
$\text{}^{\bot _{i}}{\mathcal{C}}\subset \text{}^{\bot _{1}}{\mathcal{Y}}_{i}$
, and
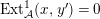 $Ext_{{\mathcal{A}}}^{1}(x,y^{\prime })=0$
. Hence the middle column splits, and we can replace
$Ext_{{\mathcal{A}}}^{1}(x,y^{\prime })=0$
. Hence the middle column splits, and we can replace
![]() $a$
by
$a$
by
![]() $x\oplus y^{\prime }$
. By the definition of
$x\oplus y^{\prime }$
. By the definition of
![]() ${\mathcal{Y}}_{i}$
, there is an exact sequence
${\mathcal{Y}}_{i}$
, there is an exact sequence
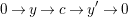 $$\begin{eqnarray}0\rightarrow y\rightarrow c\rightarrow y^{\prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow y\rightarrow c\rightarrow y^{\prime }\rightarrow 0\end{eqnarray}$$
of
![]() ${\mathcal{A}}$
such that
${\mathcal{A}}$
such that
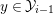 $y\in {\mathcal{Y}}_{i-1}$
and
$y\in {\mathcal{Y}}_{i-1}$
and
![]() $c\in {\mathcal{C}}$
. Then adding
$c\in {\mathcal{C}}$
. Then adding
![]() $1_{x}$
to this sequence, we get
$1_{x}$
to this sequence, we get
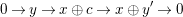 $$\begin{eqnarray}0\rightarrow y\rightarrow x\oplus c\rightarrow x\oplus y^{\prime }\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow y\rightarrow x\oplus c\rightarrow x\oplus y^{\prime }\rightarrow 0\end{eqnarray}$$
is exact. Pulling back this exact sequence with
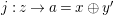 $j:z\rightarrow a=x\oplus y^{\prime }$
, we get a commutative diagram with exact rows and columns
$j:z\rightarrow a=x\oplus y^{\prime }$
, we get a commutative diagram with exact rows and columns

As
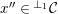 $x^{\prime \prime }\in \text{}^{\bot _{1}}{\mathcal{C}}$
, the middle column is
$x^{\prime \prime }\in \text{}^{\bot _{1}}{\mathcal{C}}$
, the middle column is
![]() ${\mathcal{C}}$
-exact. As
${\mathcal{C}}$
-exact. As
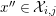 $x^{\prime \prime }\in {\mathcal{X}}_{i,j}$
and
$x^{\prime \prime }\in {\mathcal{X}}_{i,j}$
and
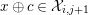 $x\oplus c\in {\mathcal{X}}_{i,j+1}$
, we have that
$x\oplus c\in {\mathcal{X}}_{i,j+1}$
, we have that
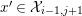 $x^{\prime }\in {\mathcal{X}}_{i-1,j+1}$
. As the top row shows,
$x^{\prime }\in {\mathcal{X}}_{i-1,j+1}$
. As the top row shows,
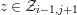 $z\in {\mathcal{Z}}_{i-1,j+1}$
, as desired. ◻
$z\in {\mathcal{Z}}_{i-1,j+1}$
, as desired. ◻
Theorem 3.16. Let
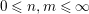 $0\leqslant n,m\leqslant \infty$
, and assume that
$0\leqslant n,m\leqslant \infty$
, and assume that
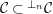 ${\mathcal{C}}\subset \text{}^{\bot _{n}}{\mathcal{C}}$
(that is,
${\mathcal{C}}\subset \text{}^{\bot _{n}}{\mathcal{C}}$
(that is,
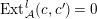 $Ext_{{\mathcal{A}}}^{l}(c,c^{\prime })=0$
for
$Ext_{{\mathcal{A}}}^{l}(c,c^{\prime })=0$
for
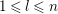 $1\leqslant l\leqslant n$
and
$1\leqslant l\leqslant n$
and
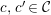 $c,c^{\prime }\in {\mathcal{C}}$
). For
$c,c^{\prime }\in {\mathcal{C}}$
). For
![]() $z\in {\mathcal{A}}$
, the following are equivalent.
$z\in {\mathcal{A}}$
, the following are equivalent.
-
(1)
 $z\in {\mathcal{Z}}_{n,m}$
.
$z\in {\mathcal{Z}}_{n,m}$
. -
(2) There is an exact sequence
(4)such that $$\begin{eqnarray}0\rightarrow x_{n}\xrightarrow[{}]{d_{n}}x_{n-1}\xrightarrow[{}]{d_{n-1}}x_{0}\xrightarrow[{}]{\unicode[STIX]{x1D700}}z\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow x_{n}\xrightarrow[{}]{d_{n}}x_{n-1}\xrightarrow[{}]{d_{n-1}}x_{0}\xrightarrow[{}]{\unicode[STIX]{x1D700}}z\rightarrow 0\end{eqnarray}$$
 $x_{i}\in {\mathcal{X}}_{n-i,m+i}$
.
$x_{i}\in {\mathcal{X}}_{n-i,m+i}$
.
If, moreover, for each
![]() $a\in {\mathcal{A}}$
, there is a surjection
$a\in {\mathcal{A}}$
, there is a surjection
![]() $x\rightarrow a$
with
$x\rightarrow a$
with
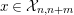 $x\in {\mathcal{X}}_{n,n+m}$
, then these conditions are equivalent to the following.
$x\in {\mathcal{X}}_{n,n+m}$
, then these conditions are equivalent to the following.
-
(3) For each exact sequence (4) with
 $x_{i}\in {\mathcal{X}}_{n-i,m+i+1}$
for
$x_{i}\in {\mathcal{X}}_{n-i,m+i+1}$
for
 $0\leqslant i\leqslant n-1$
, we have that
$0\leqslant i\leqslant n-1$
, we have that
 $x_{n}\in {\mathcal{X}}_{0,n+m}$
.
$x_{n}\in {\mathcal{X}}_{0,n+m}$
.
Proof. (1)
![]() $\Rightarrow$
(2). There is an exact sequence
$\Rightarrow$
(2). There is an exact sequence
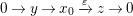 $0\rightarrow y\rightarrow x_{0}\xrightarrow[{}]{\unicode[STIX]{x1D700}}z\rightarrow 0$
with
$0\rightarrow y\rightarrow x_{0}\xrightarrow[{}]{\unicode[STIX]{x1D700}}z\rightarrow 0$
with
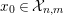 $x_{0}\in {\mathcal{X}}_{n,m}$
and
$x_{0}\in {\mathcal{X}}_{n,m}$
and
![]() $y\in {\mathcal{Y}}_{n}$
. So there is an exact sequence
$y\in {\mathcal{Y}}_{n}$
. So there is an exact sequence
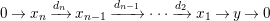 $$\begin{eqnarray}0\rightarrow x_{n}\xrightarrow[{}]{d_{n}}x_{n-1}\xrightarrow[{}]{d_{n-1}}\cdots \xrightarrow[{}]{d_{2}}x_{1}\rightarrow y\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow x_{n}\xrightarrow[{}]{d_{n}}x_{n-1}\xrightarrow[{}]{d_{n-1}}\cdots \xrightarrow[{}]{d_{2}}x_{1}\rightarrow y\rightarrow 0\end{eqnarray}$$
with
![]() $x_{i}\in {\mathcal{C}}$
for
$x_{i}\in {\mathcal{C}}$
for
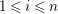 $1\leqslant i\leqslant n$
. As
$1\leqslant i\leqslant n$
. As
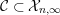 ${\mathcal{C}}\subset {\mathcal{X}}_{n,\infty }$
, we are done.
${\mathcal{C}}\subset {\mathcal{X}}_{n,\infty }$
, we are done.
(2)
![]() $\Rightarrow$
(1). Let
$\Rightarrow$
(1). Let
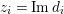 $z_{i}= Imd_{i}$
for
$z_{i}= Imd_{i}$
for
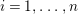 $i=1,\ldots ,n$
, and
$i=1,\ldots ,n$
, and
![]() $z_{0}:=z$
. Then by descending induction on
$z_{0}:=z$
. Then by descending induction on
![]() $i$
, we can prove
$i$
, we can prove
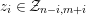 $z_{i}\in {\mathcal{Z}}_{n-i,m+i}$
for
$z_{i}\in {\mathcal{Z}}_{n-i,m+i}$
for
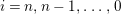 $i=n,n-1,\ldots ,0$
, using Lemma 3.14 easily.
$i=n,n-1,\ldots ,0$
, using Lemma 3.14 easily.
(1)
![]() $\Rightarrow$
(3) is also proved easily, using Lemma 3.15.
$\Rightarrow$
(3) is also proved easily, using Lemma 3.15.
(3)
![]() $\Rightarrow$
(2) is trivial.◻
$\Rightarrow$
(2) is trivial.◻
4
 $(n,C)$
-TF property
$(n,C)$
-TF property
4.1
In the rest of this paper, let
![]() $\unicode[STIX]{x1D6EC}$
be a module-finite
$\unicode[STIX]{x1D6EC}$
be a module-finite
![]() $R$
-algebra, which need not be commutative. A
$R$
-algebra, which need not be commutative. A
![]() $\unicode[STIX]{x1D6EC}$
-bimodule means a
$\unicode[STIX]{x1D6EC}$
-bimodule means a
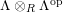 $\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}$
-module. Let
$\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}$
-module. Let
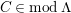 $C\in mod\unicode[STIX]{x1D6EC}$
be fixed. Set
$C\in mod\unicode[STIX]{x1D6EC}$
be fixed. Set
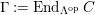 $\unicode[STIX]{x1D6E4}:= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Note that
$\unicode[STIX]{x1D6E4}:= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Note that
![]() $\unicode[STIX]{x1D6E4}$
is also a module-finite
$\unicode[STIX]{x1D6E4}$
is also a module-finite
![]() $R$
-algebra. We denote
$R$
-algebra. We denote
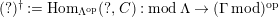 $(?)^{\dagger }:= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C): mod\unicode[STIX]{x1D6EC}\rightarrow (\unicode[STIX]{x1D6E4}{\rm mod})^{op}$
, and
$(?)^{\dagger }:= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C): mod\unicode[STIX]{x1D6EC}\rightarrow (\unicode[STIX]{x1D6E4}{\rm mod})^{op}$
, and
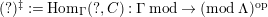 $(?)^{\ddagger }:= Hom_{\unicode[STIX]{x1D6E4}}(?,C):\unicode[STIX]{x1D6E4}{\rm mod}\rightarrow ({\rm mod}\unicode[STIX]{x1D6EC})^{op}$
.
$(?)^{\ddagger }:= Hom_{\unicode[STIX]{x1D6E4}}(?,C):\unicode[STIX]{x1D6E4}{\rm mod}\rightarrow ({\rm mod}\unicode[STIX]{x1D6EC})^{op}$
.
4.2
We denote
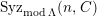 $Syz_{{\rm mod}\unicode[STIX]{x1D6EC}}(n,C)$
,
$Syz_{{\rm mod}\unicode[STIX]{x1D6EC}}(n,C)$
,
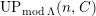 $UP_{{\rm mod}\unicode[STIX]{x1D6EC}}(n,C)$
, and
$UP_{{\rm mod}\unicode[STIX]{x1D6EC}}(n,C)$
, and
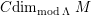 $Cdim_{{\rm mod}\unicode[STIX]{x1D6EC}}M$
respectively by
$Cdim_{{\rm mod}\unicode[STIX]{x1D6EC}}M$
respectively by
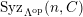 $Syz_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
,
$Syz_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
,
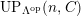 $UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
, and
$UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
, and
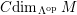 $Cdim_{\unicode[STIX]{x1D6EC}^{op}}M$
.
$Cdim_{\unicode[STIX]{x1D6EC}^{op}}M$
.
4.3
Note that for
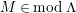 $M\in mod\unicode[STIX]{x1D6EC}$
and
$M\in mod\unicode[STIX]{x1D6EC}$
and
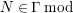 $N\in \unicode[STIX]{x1D6E4}{\rm mod}$
, we have standard isomorphisms
$N\in \unicode[STIX]{x1D6E4}{\rm mod}$
, we have standard isomorphisms
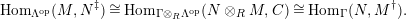 $$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,N^{\ddagger })\cong Hom_{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}(N\otimes _{R}M,C)\cong Hom_{\unicode[STIX]{x1D6E4}}(N,M^{\dagger }).\end{eqnarray}$$
$$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,N^{\ddagger })\cong Hom_{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}(N\otimes _{R}M,C)\cong Hom_{\unicode[STIX]{x1D6E4}}(N,M^{\dagger }).\end{eqnarray}$$
The first isomorphism sends
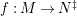 $f:M\rightarrow N^{\ddagger }$
to the map
$f:M\rightarrow N^{\ddagger }$
to the map
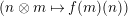 $(n\otimes m\mapsto f(m)(n))$
. Its inverse is given by
$(n\otimes m\mapsto f(m)(n))$
. Its inverse is given by
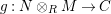 $g:N\otimes _{R}M\rightarrow C$
to
$g:N\otimes _{R}M\rightarrow C$
to
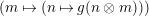 $(m\mapsto (n\mapsto g(n\otimes m)))$
. This shows that
$(m\mapsto (n\mapsto g(n\otimes m)))$
. This shows that
![]() $(?)^{\dagger }$
has
$(?)^{\dagger }$
has
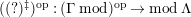 $((?)^{\ddagger })^{op}:(\unicode[STIX]{x1D6E4}{\rm mod})^{op}\rightarrow mod\unicode[STIX]{x1D6EC}$
as a right adjoint. Hence
$((?)^{\ddagger })^{op}:(\unicode[STIX]{x1D6E4}{\rm mod})^{op}\rightarrow mod\unicode[STIX]{x1D6EC}$
as a right adjoint. Hence
![]() $((?)^{\dagger })^{op}$
is right adjoint to
$((?)^{\dagger })^{op}$
is right adjoint to
![]() $(?)^{\ddagger }$
. We denote the unit of adjunction
$(?)^{\ddagger }$
. We denote the unit of adjunction
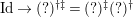 $\operatorname{Id}\rightarrow (?)^{\dagger \ddagger }=(?)^{\ddagger }(?)^{\dagger }$
by
$\operatorname{Id}\rightarrow (?)^{\dagger \ddagger }=(?)^{\ddagger }(?)^{\dagger }$
by
![]() $\unicode[STIX]{x1D706}$
. Note that for
$\unicode[STIX]{x1D706}$
. Note that for
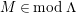 $M\in mod\unicode[STIX]{x1D6EC}$
, the map
$M\in mod\unicode[STIX]{x1D6EC}$
, the map
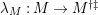 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is given by
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is given by
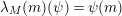 $\unicode[STIX]{x1D706}_{M}(m)(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D713}(m)$
for
$\unicode[STIX]{x1D706}_{M}(m)(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D713}(m)$
for
![]() $m\in M$
and
$m\in M$
and
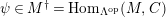 $\unicode[STIX]{x1D713}\in M^{\dagger }= Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,C)$
. We denote the unit of adjunction
$\unicode[STIX]{x1D713}\in M^{\dagger }= Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,C)$
. We denote the unit of adjunction
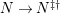 $N\rightarrow N^{\ddagger \dagger }$
by
$N\rightarrow N^{\ddagger \dagger }$
by
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{N}$
for
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{N}$
for
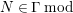 $N\in \unicode[STIX]{x1D6E4}{\rm mod}$
. When we view
$N\in \unicode[STIX]{x1D6E4}{\rm mod}$
. When we view
![]() $\unicode[STIX]{x1D707}$
as a morphism
$\unicode[STIX]{x1D707}$
as a morphism
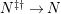 $N^{\ddagger \dagger }\rightarrow N$
(in the opposite category
$N^{\ddagger \dagger }\rightarrow N$
(in the opposite category
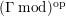 $(\unicode[STIX]{x1D6E4}{\rm mod})^{op}$
), then it is the counit of adjunction.
$(\unicode[STIX]{x1D6E4}{\rm mod})^{op}$
), then it is the counit of adjunction.
Lemma 4.4.
![]() $(?)^{\dagger }$
and
$(?)^{\dagger }$
and
![]() $(?)^{\ddagger }$
give a contravariant equivalence between
$(?)^{\ddagger }$
give a contravariant equivalence between
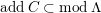 $addC\subset mod\unicode[STIX]{x1D6EC}$
and
$addC\subset mod\unicode[STIX]{x1D6EC}$
and
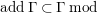 $add\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}{\rm mod}$
.
$add\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}{\rm mod}$
.
Proof. It suffices to show that
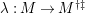 $\unicode[STIX]{x1D706}:M\rightarrow M^{\dagger \ddagger }$
is an isomorphism for
$\unicode[STIX]{x1D706}:M\rightarrow M^{\dagger \ddagger }$
is an isomorphism for
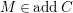 $M\in addC$
, and
$M\in addC$
, and
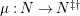 $\unicode[STIX]{x1D707}:N\rightarrow N^{\ddagger \dagger }$
is an isomorphism for
$\unicode[STIX]{x1D707}:N\rightarrow N^{\ddagger \dagger }$
is an isomorphism for
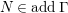 $N\in add\unicode[STIX]{x1D6E4}$
. To verify this, we may assume that
$N\in add\unicode[STIX]{x1D6E4}$
. To verify this, we may assume that
![]() $M=C$
and
$M=C$
and
![]() $N=\unicode[STIX]{x1D6E4}$
. This case is trivial.◻
$N=\unicode[STIX]{x1D6E4}$
. This case is trivial.◻
Definition 4.5. (cf. [Reference TakahashiTak, (2.2)])
Let
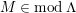 $M\in mod\unicode[STIX]{x1D6EC}$
. We say that
$M\in mod\unicode[STIX]{x1D6EC}$
. We say that
![]() $M$
is
$M$
is
![]() $(1,C)$
-TF or
$(1,C)$
-TF or
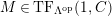 $M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
if
$M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
if
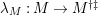 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is injective. We say that
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is injective. We say that
![]() $M$
is
$M$
is
![]() $(2,C)$
-TF or
$(2,C)$
-TF or
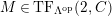 $M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(2,C)$
if
$M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(2,C)$
if
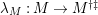 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is bijective. Let
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is bijective. Let
![]() $n\geqslant 3$
. We say that
$n\geqslant 3$
. We say that
![]() $M$
is
$M$
is
![]() $(n,C)$
-TF or
$(n,C)$
-TF or
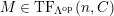 $M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
if
$M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
if
![]() $M$
is
$M$
is
![]() $(2,C)$
-TF and
$(2,C)$
-TF and
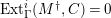 $Ext_{\unicode[STIX]{x1D6E4}}^{i}(M^{\dagger },C)=0$
for
$Ext_{\unicode[STIX]{x1D6E4}}^{i}(M^{\dagger },C)=0$
for
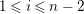 $1\leqslant i\leqslant n-2$
. As a convention, we define that any
$1\leqslant i\leqslant n-2$
. As a convention, we define that any
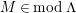 $M\in mod\unicode[STIX]{x1D6EC}$
is
$M\in mod\unicode[STIX]{x1D6EC}$
is
![]() $(0,C)$
-TF.
$(0,C)$
-TF.
Lemma 4.6. Let
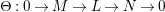 $\unicode[STIX]{x1D6E9}:0\rightarrow M\rightarrow L\rightarrow N\rightarrow 0$
be a
$\unicode[STIX]{x1D6E9}:0\rightarrow M\rightarrow L\rightarrow N\rightarrow 0$
be a
![]() $C$
-exact sequence in
$C$
-exact sequence in
![]() ${\rm mod}\unicode[STIX]{x1D6EC}$
. Then for
${\rm mod}\unicode[STIX]{x1D6EC}$
. Then for
![]() $n\geqslant 0$
, we have the following.
$n\geqslant 0$
, we have the following.
-
(1) If
 $M\in TF(n,C)$
and
$M\in TF(n,C)$
and
 $N\in TF(n,C)$
, then
$N\in TF(n,C)$
, then
 $L\in TF(n,C)$
.
$L\in TF(n,C)$
. -
(2) If
 $L\in TF(n+1,C)$
and
$L\in TF(n+1,C)$
and
 $N\in TF(n,C)$
, then
$N\in TF(n,C)$
, then
 $M\in TF(n+1,C)$
.
$M\in TF(n+1,C)$
. -
(3) If
 $M\in TF(n+1,C)$
and
$M\in TF(n+1,C)$
and
 $L\in TF(n,C)$
, then
$L\in TF(n,C)$
, then
 $N\in TF(n,C)$
.
$N\in TF(n,C)$
.
Proof. We have a commutative diagram
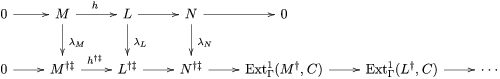
with exact rows.
We only prove (3). We may assume that
![]() $n\geqslant 1$
. So
$n\geqslant 1$
. So
![]() $\unicode[STIX]{x1D706}_{M}$
is an isomorphism and
$\unicode[STIX]{x1D706}_{M}$
is an isomorphism and
![]() $\unicode[STIX]{x1D706}_{L}$
is injective. By the five lemma,
$\unicode[STIX]{x1D706}_{L}$
is injective. By the five lemma,
![]() $\unicode[STIX]{x1D706}_{N}$
is injective, and the case that
$\unicode[STIX]{x1D706}_{N}$
is injective, and the case that
![]() $n=1$
has been done. If
$n=1$
has been done. If
![]() $n\geqslant 2$
, then
$n\geqslant 2$
, then
![]() $\unicode[STIX]{x1D706}_{L}$
is also an isomorphism and
$\unicode[STIX]{x1D706}_{L}$
is also an isomorphism and
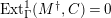 $Ext_{\unicode[STIX]{x1D6E4}}^{1}(M^{\dagger },C)=0$
, and so
$Ext_{\unicode[STIX]{x1D6E4}}^{1}(M^{\dagger },C)=0$
, and so
![]() $\unicode[STIX]{x1D706}_{N}$
is an isomorphism. Moreover, for
$\unicode[STIX]{x1D706}_{N}$
is an isomorphism. Moreover, for
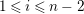 $1\leqslant i\leqslant n-2$
,
$1\leqslant i\leqslant n-2$
,
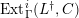 $Ext_{\unicode[STIX]{x1D6E4}}^{i}(L^{\dagger },C)$
and
$Ext_{\unicode[STIX]{x1D6E4}}^{i}(L^{\dagger },C)$
and
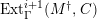 $Ext_{\unicode[STIX]{x1D6E4}}^{i+1}(M^{\dagger },C)$
vanish. so
$Ext_{\unicode[STIX]{x1D6E4}}^{i+1}(M^{\dagger },C)$
vanish. so
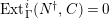 $Ext_{\unicode[STIX]{x1D6E4}}^{i}(N^{\dagger },C)=0$
for
$Ext_{\unicode[STIX]{x1D6E4}}^{i}(N^{\dagger },C)=0$
for
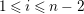 $1\leqslant i\leqslant n-2$
, and hence
$1\leqslant i\leqslant n-2$
, and hence
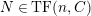 $N\in TF(n,C)$
.
$N\in TF(n,C)$
.
(1) and (2) are also proved similarly. ◻
Lemma 4.7. (cf. [Reference TakahashiTak, Proposition 3.2])
-
(1) For
 $n=0,1$
,
$n=0,1$
,
 $Syz_{\unicode[STIX]{x1D6EC}^{op}}(n,C)= UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
.
$Syz_{\unicode[STIX]{x1D6EC}^{op}}(n,C)= UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
. -
(2) For
 $n\geqslant 0$
,
$n\geqslant 0$
,
 $TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)= UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
.
$TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)= UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
.
Proof. If
![]() $n=0$
, then
$n=0$
, then
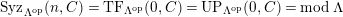 $Syz_{\unicode[STIX]{x1D6EC}^{op}}(n,C)= TF_{\unicode[STIX]{x1D6EC}^{op}}(0,C)= UP_{\unicode[STIX]{x1D6EC}^{op}}(0,C)= mod\unicode[STIX]{x1D6EC}$
. So we may assume that
$Syz_{\unicode[STIX]{x1D6EC}^{op}}(n,C)= TF_{\unicode[STIX]{x1D6EC}^{op}}(0,C)= UP_{\unicode[STIX]{x1D6EC}^{op}}(0,C)= mod\unicode[STIX]{x1D6EC}$
. So we may assume that
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Let
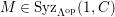 $M\in Syz_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
. Then there is an injection
$M\in Syz_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
. Then there is an injection
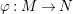 $\unicode[STIX]{x1D711}:M\rightarrow N$
with
$\unicode[STIX]{x1D711}:M\rightarrow N$
with
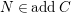 $N\in addC$
. Then
$N\in addC$
. Then
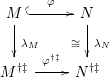
is a commutative diagram. So
![]() $\unicode[STIX]{x1D706}_{M}$
is injective, and
$\unicode[STIX]{x1D706}_{M}$
is injective, and
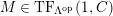 $M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
. This shows
$M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
. This shows
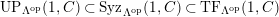 $UP_{\unicode[STIX]{x1D6EC}^{op}}(1,C)\subset Syz_{\unicode[STIX]{x1D6EC}^{op}}(1,C)\subset TF_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
. So (2)
$UP_{\unicode[STIX]{x1D6EC}^{op}}(1,C)\subset Syz_{\unicode[STIX]{x1D6EC}^{op}}(1,C)\subset TF_{\unicode[STIX]{x1D6EC}^{op}}(1,C)$
. So (2)
![]() $\Rightarrow$
(1).
$\Rightarrow$
(1).
We prove (2). First, we prove
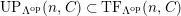 $UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)\subset TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
for
$UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)\subset TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
for
![]() $n\geqslant 1$
. We use induction on
$n\geqslant 1$
. We use induction on
![]() $n$
. The case
$n$
. The case
![]() $n=1$
is already done above.
$n=1$
is already done above.
Let
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
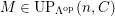 $M\in UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
. Then by the definition of
$M\in UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
. Then by the definition of
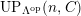 $UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
, there is a
$UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
, there is a
![]() $C$
-exact sequence
$C$
-exact sequence
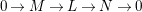 $$\begin{eqnarray}0\rightarrow M\rightarrow L\rightarrow N\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\rightarrow L\rightarrow N\rightarrow 0\end{eqnarray}$$
such that
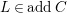 $L\in addC$
and
$L\in addC$
and
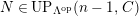 $N\in UP_{\unicode[STIX]{x1D6EC}^{op}}(n-1,C)$
. By induction hypothesis,
$N\in UP_{\unicode[STIX]{x1D6EC}^{op}}(n-1,C)$
. By induction hypothesis,
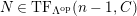 $N\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n-1,C)$
. Hence
$N\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n-1,C)$
. Hence
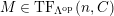 $M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
by Lemma 4.6. We have proved that
$M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
by Lemma 4.6. We have proved that
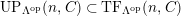 $UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)\subset TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
.
$UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)\subset TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
.
Next we show that
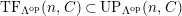 $TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)\subset UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
for
$TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)\subset UP_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
for
![]() $n\geqslant 1$
. We use induction on
$n\geqslant 1$
. We use induction on
![]() $n$
.
$n$
.
Let
![]() $n=1$
. Let
$n=1$
. Let
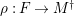 $\unicode[STIX]{x1D70C}:F\rightarrow M^{\dagger }$
be any surjective
$\unicode[STIX]{x1D70C}:F\rightarrow M^{\dagger }$
be any surjective
![]() $\unicode[STIX]{x1D6E4}$
-linear map with
$\unicode[STIX]{x1D6E4}$
-linear map with
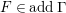 $F\in add\unicode[STIX]{x1D6E4}$
. Then the map
$F\in add\unicode[STIX]{x1D6E4}$
. Then the map
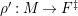 $\unicode[STIX]{x1D70C}^{\prime }:M\rightarrow F^{\ddagger }$
which corresponds to
$\unicode[STIX]{x1D70C}^{\prime }:M\rightarrow F^{\ddagger }$
which corresponds to
![]() $\unicode[STIX]{x1D70C}$
by the adjunction (5) is
$\unicode[STIX]{x1D70C}$
by the adjunction (5) is
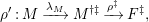 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\prime }:M\xrightarrow[{}]{\unicode[STIX]{x1D706}_{M}}M^{\dagger \ddagger }\xrightarrow[{}]{\unicode[STIX]{x1D70C}^{\ddagger }}F^{\ddagger },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\prime }:M\xrightarrow[{}]{\unicode[STIX]{x1D706}_{M}}M^{\dagger \ddagger }\xrightarrow[{}]{\unicode[STIX]{x1D70C}^{\ddagger }}F^{\ddagger },\end{eqnarray}$$
which is injective by assumption. Then
![]() $\unicode[STIX]{x1D70C}$
is the composite
$\unicode[STIX]{x1D70C}$
is the composite
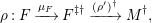 $$\begin{eqnarray}\unicode[STIX]{x1D70C}:F\xrightarrow[{}]{\unicode[STIX]{x1D707}_{F}}F^{\ddagger \dagger }\xrightarrow[{}]{(\unicode[STIX]{x1D70C}^{\prime })^{\dagger }}M^{\dagger },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:F\xrightarrow[{}]{\unicode[STIX]{x1D707}_{F}}F^{\ddagger \dagger }\xrightarrow[{}]{(\unicode[STIX]{x1D70C}^{\prime })^{\dagger }}M^{\dagger },\end{eqnarray}$$
which is a surjective map by assumption. So
![]() $(\unicode[STIX]{x1D70C}^{\prime })^{\dagger }$
is also surjective, and hence
$(\unicode[STIX]{x1D70C}^{\prime })^{\dagger }$
is also surjective, and hence
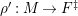 $\unicode[STIX]{x1D70C}^{\prime }:M\rightarrow F^{\ddagger }$
gives a
$\unicode[STIX]{x1D70C}^{\prime }:M\rightarrow F^{\ddagger }$
gives a
![]() $(1,C)$
-universal pushforward.
$(1,C)$
-universal pushforward.
Now let
![]() $n\geqslant 2$
. By what we have proved,
$n\geqslant 2$
. By what we have proved,
![]() $M$
has a
$M$
has a
![]() $(1,C)$
-universal pushforward
$(1,C)$
-universal pushforward
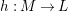 $h:M\rightarrow L$
. Let
$h:M\rightarrow L$
. Let
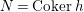 $N= Cokerh$
. Then we have a
$N= Cokerh$
. Then we have a
![]() $C$
-exact sequence
$C$
-exact sequence
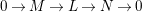 $$\begin{eqnarray}0\rightarrow M\rightarrow L\rightarrow N\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow M\rightarrow L\rightarrow N\rightarrow 0\end{eqnarray}$$
with
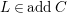 $L\in addC$
. As
$L\in addC$
. As
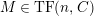 $M\in TF(n,C)$
,
$M\in TF(n,C)$
,
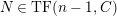 $N\in TF(n-1,C)$
by Lemma 4.6. By induction hypothesis,
$N\in TF(n-1,C)$
by Lemma 4.6. By induction hypothesis,
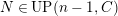 $N\in UP(n-1,C)$
. So by the definition of
$N\in UP(n-1,C)$
. So by the definition of
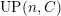 $UP(n,C)$
, we have that
$UP(n,C)$
, we have that
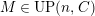 $M\in UP(n,C)$
, as desired.◻
$M\in UP(n,C)$
, as desired.◻
Lemma 4.8. For any
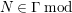 $N\in \unicode[STIX]{x1D6E4}{\rm mod}$
, we have that
$N\in \unicode[STIX]{x1D6E4}{\rm mod}$
, we have that
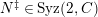 $N^{\ddagger }\in Syz(2,C)$
.
$N^{\ddagger }\in Syz(2,C)$
.
Proof. Let
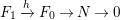 $$\begin{eqnarray}F_{1}\xrightarrow[{}]{h}F_{0}\rightarrow N\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}F_{1}\xrightarrow[{}]{h}F_{0}\rightarrow N\rightarrow 0\end{eqnarray}$$
be an exact sequence in
![]() $\unicode[STIX]{x1D6E4}{\rm mod}$
such that
$\unicode[STIX]{x1D6E4}{\rm mod}$
such that
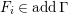 $F_{i}\in add\unicode[STIX]{x1D6E4}$
. Then
$F_{i}\in add\unicode[STIX]{x1D6E4}$
. Then
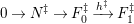 $$\begin{eqnarray}0\rightarrow N^{\ddagger }\rightarrow F_{0}^{\ddagger }\xrightarrow[{}]{h^{\ddagger }}F_{1}^{\ddagger }\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow N^{\ddagger }\rightarrow F_{0}^{\ddagger }\xrightarrow[{}]{h^{\ddagger }}F_{1}^{\ddagger }\end{eqnarray}$$
is exact, and
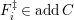 $F_{i}^{\ddagger }\in addC$
. This shows that
$F_{i}^{\ddagger }\in addC$
. This shows that
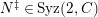 $N^{\ddagger }\in Syz(2,C)$
.◻
$N^{\ddagger }\in Syz(2,C)$
.◻
4.9
We denote by
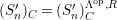 $(S_{n}^{\prime })_{C}=(S_{n}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
the class of
$(S_{n}^{\prime })_{C}=(S_{n}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
the class of
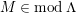 $M\in mod\unicode[STIX]{x1D6EC}$
such that
$M\in mod\unicode[STIX]{x1D6EC}$
such that
![]() $M$
viewed as an
$M$
viewed as an
![]() $R$
-module lies in
$R$
-module lies in
![]() $(S_{n}^{\prime })_{C}^{R}$
; see (2.15).
$(S_{n}^{\prime })_{C}^{R}$
; see (2.15).
Lemma 4.10. Assume that
![]() $C$
satisfies
$C$
satisfies
![]() $(S_{n}^{\prime })$
as an
$(S_{n}^{\prime })$
as an
![]() $R$
-module. Then
$R$
-module. Then
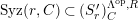 $Syz(r,C)\subset (S_{r}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
for
$Syz(r,C)\subset (S_{r}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
for
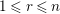 $1\leqslant r\leqslant n$
.
$1\leqslant r\leqslant n$
.
Proof. This follows easily from Corollary 2.9. ◻
4.11
For an additive category
![]() ${\mathcal{C}}$
and its additive subcategory
${\mathcal{C}}$
and its additive subcategory
![]() ${\mathcal{X}}$
, we denote by
${\mathcal{X}}$
, we denote by
![]() ${\mathcal{C}}/{\mathcal{X}}$
the quotient of
${\mathcal{C}}/{\mathcal{X}}$
the quotient of
![]() ${\mathcal{C}}$
divided by the ideal consisting of morphisms which factor through objects of
${\mathcal{C}}$
divided by the ideal consisting of morphisms which factor through objects of
![]() ${\mathcal{X}}$
.
${\mathcal{X}}$
.
4.12
For each
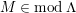 $M\in mod\unicode[STIX]{x1D6EC}$
, take a presentation
$M\in mod\unicode[STIX]{x1D6EC}$
, take a presentation
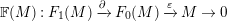 $$\begin{eqnarray}\mathbb{F}(M):F_{1}(M)\xrightarrow[{}]{\unicode[STIX]{x2202}}F_{0}(M)\xrightarrow[{}]{\unicode[STIX]{x1D700}}M\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{F}(M):F_{1}(M)\xrightarrow[{}]{\unicode[STIX]{x2202}}F_{0}(M)\xrightarrow[{}]{\unicode[STIX]{x1D700}}M\rightarrow 0\end{eqnarray}$$
with
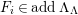 $F_{i}\in add\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
. We denote
$F_{i}\in add\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
. We denote
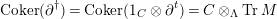 $$\begin{eqnarray}Coker(\unicode[STIX]{x2202}^{\dagger })= Coker(1_{C}\otimes \unicode[STIX]{x2202}^{t})=C\otimes _{\unicode[STIX]{x1D6EC}}TrM\end{eqnarray}$$
$$\begin{eqnarray}Coker(\unicode[STIX]{x2202}^{\dagger })= Coker(1_{C}\otimes \unicode[STIX]{x2202}^{t})=C\otimes _{\unicode[STIX]{x1D6EC}}TrM\end{eqnarray}$$
by
![]() $Tr_{C}M$
, where
$Tr_{C}M$
, where
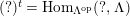 $(?)^{t}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,\unicode[STIX]{x1D6EC})$
and
$(?)^{t}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,\unicode[STIX]{x1D6EC})$
and
![]() $Tr$
is the transpose (see [Reference Assem, Simson and SkowrońskiASS, (V.2)]), and we call it the
$Tr$
is the transpose (see [Reference Assem, Simson and SkowrońskiASS, (V.2)]), and we call it the
![]() $C$
-transpose of
$C$
-transpose of
![]() $M$
.
$M$
.
![]() $Tr_{C}$
is an additive functor from
$Tr_{C}$
is an additive functor from
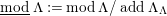 $\operatorname{mod̲}\unicode[STIX]{x1D6EC}:= mod\unicode[STIX]{x1D6EC}/add\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
to
$\operatorname{mod̲}\unicode[STIX]{x1D6EC}:= mod\unicode[STIX]{x1D6EC}/add\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
to
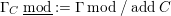 $\unicode[STIX]{x1D6E4}_{C}\operatorname{mod̲}:=\unicode[STIX]{x1D6E4}{\rm mod}/addC$
.
$\unicode[STIX]{x1D6E4}_{C}\operatorname{mod̲}:=\unicode[STIX]{x1D6E4}{\rm mod}/addC$
.
Proposition 4.13. Let
![]() $n\geqslant 0$
, and assume that
$n\geqslant 0$
, and assume that
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
is
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
is
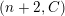 $(n+2,C)$
-TF. Then for
$(n+2,C)$
-TF. Then for
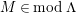 $M\in mod\unicode[STIX]{x1D6EC}$
, we have the following.
$M\in mod\unicode[STIX]{x1D6EC}$
, we have the following.
- (0)
-
For
 $1\leqslant i\leqslant n$
,
$1\leqslant i\leqslant n$
,
 $Ext_{\unicode[STIX]{x1D6E4}}^{i}(Tr_{C}?,C)$
is a well-defined additive functor
$Ext_{\unicode[STIX]{x1D6E4}}^{i}(Tr_{C}?,C)$
is a well-defined additive functor
 $\operatorname{mod̲}\unicode[STIX]{x1D6EC}\rightarrow {\rm mod}\unicode[STIX]{x1D6EC}$
.
$\operatorname{mod̲}\unicode[STIX]{x1D6EC}\rightarrow {\rm mod}\unicode[STIX]{x1D6EC}$
. - (1)
-
If
 $n=1$
, there is an exact sequence
$n=1$
, there is an exact sequence  $$\begin{eqnarray}0\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{1}(Tr_{C}M,C)\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x1D706}_{M}}M^{\dagger \ddagger }\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{2}(Tr_{C}M,C).\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{1}(Tr_{C}M,C)\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x1D706}_{M}}M^{\dagger \ddagger }\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{2}(Tr_{C}M,C).\end{eqnarray}$$
If
 $n=0$
, then there is an injective homomorphism
$n=0$
, then there is an injective homomorphism
 $Ker\unicode[STIX]{x1D706}_{M}{\hookrightarrow}Ext_{\unicode[STIX]{x1D6E4}}^{1}(Tr_{C}M,C)$
.
$Ker\unicode[STIX]{x1D706}_{M}{\hookrightarrow}Ext_{\unicode[STIX]{x1D6E4}}^{1}(Tr_{C}M,C)$
. - (2)
-
If
 $n\geqslant 2$
, then
$n\geqslant 2$
, then-
(i) There is an exact sequence
 $$\begin{eqnarray}0\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{1}(Tr_{C}M,C)\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x1D706}_{M}}M^{\dagger \ddagger }\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{2}(Tr_{C}M,C)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{1}(Tr_{C}M,C)\rightarrow M\xrightarrow[{}]{\unicode[STIX]{x1D706}_{M}}M^{\dagger \ddagger }\rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{2}(Tr_{C}M,C)\rightarrow 0.\end{eqnarray}$$
-
(ii) There are isomorphisms
 $Ext^{i+2}\unicode[STIX]{x1D6E4}(Tr_{C}M,C)\cong Ext_{\unicode[STIX]{x1D6E4}}^{i}(M^{\dagger },C)$
for
$Ext^{i+2}\unicode[STIX]{x1D6E4}(Tr_{C}M,C)\cong Ext_{\unicode[STIX]{x1D6E4}}^{i}(M^{\dagger },C)$
for
 $1\leqslant i\leqslant n-2$
.
$1\leqslant i\leqslant n-2$
. -
(iii) There is an injective map
 $Ext_{\unicode[STIX]{x1D6E4}}^{n-1}(M^{\dagger },C){\hookrightarrow}Ext_{\unicode[STIX]{x1D6E4}}^{n+1}(Tr_{C}M,C)$
.
$Ext_{\unicode[STIX]{x1D6E4}}^{n-1}(M^{\dagger },C){\hookrightarrow}Ext_{\unicode[STIX]{x1D6E4}}^{n+1}(Tr_{C}M,C)$
.
-
Proof. (0) is obvious by assumption.
We consider that
![]() $\mathbb{F}(M)$
is a complex with
$\mathbb{F}(M)$
is a complex with
![]() $M$
at degree zero. Then consider
$M$
at degree zero. Then consider
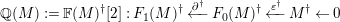 $$\begin{eqnarray}\mathbb{Q}(M):=\mathbb{F}(M)^{\dagger }[2]:F_{1}(M)^{\dagger }\xleftarrow[{}]{\unicode[STIX]{x2202}^{\dagger }}F_{0}(M)^{\dagger }\xleftarrow[{}]{\unicode[STIX]{x1D700}^{\dagger }}M^{\dagger }\leftarrow 0\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Q}(M):=\mathbb{F}(M)^{\dagger }[2]:F_{1}(M)^{\dagger }\xleftarrow[{}]{\unicode[STIX]{x2202}^{\dagger }}F_{0}(M)^{\dagger }\xleftarrow[{}]{\unicode[STIX]{x1D700}^{\dagger }}M^{\dagger }\leftarrow 0\end{eqnarray}$$
where
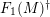 $F_{1}(M)^{\dagger }$
is at degree zero. As this complex is quasi-isomorphic to
$F_{1}(M)^{\dagger }$
is at degree zero. As this complex is quasi-isomorphic to
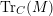 $Tr_{C}(M)$
, there is a spectral sequence
$Tr_{C}(M)$
, there is a spectral sequence
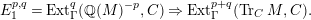 $$\begin{eqnarray}E_{1}^{p,q}= Ext_{\unicode[STIX]{x1D6E4}}^{q}(\mathbb{Q}(M)^{-p},C)\Rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{p+q}(Tr_{C}M,C).\end{eqnarray}$$
$$\begin{eqnarray}E_{1}^{p,q}= Ext_{\unicode[STIX]{x1D6E4}}^{q}(\mathbb{Q}(M)^{-p},C)\Rightarrow Ext_{\unicode[STIX]{x1D6E4}}^{p+q}(Tr_{C}M,C).\end{eqnarray}$$
In general,
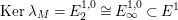 $Ker\unicode[STIX]{x1D706}_{M}=E_{2}^{1,0}\cong E_{\infty }^{1,0}\subset E^{1}$
. If
$Ker\unicode[STIX]{x1D706}_{M}=E_{2}^{1,0}\cong E_{\infty }^{1,0}\subset E^{1}$
. If
![]() $n\geqslant 1$
, then
$n\geqslant 1$
, then
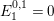 $E_{1}^{0,1}=0$
, and
$E_{1}^{0,1}=0$
, and
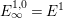 $E_{\infty }^{1,0}=E^{1}$
. Moreover, as
$E_{\infty }^{1,0}=E^{1}$
. Moreover, as
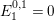 $E_{1}^{0,1}=0$
,
$E_{1}^{0,1}=0$
,
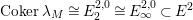 $Coker\unicode[STIX]{x1D706}_{M}\cong E_{2}^{2,0}\cong E_{\infty }^{2,0}\subset E^{2}$
. So (1) follows.
$Coker\unicode[STIX]{x1D706}_{M}\cong E_{2}^{2,0}\cong E_{\infty }^{2,0}\subset E^{2}$
. So (1) follows.
If
![]() $n\geqslant 2$
, then
$n\geqslant 2$
, then
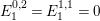 $E_{1}^{0,2}=E_{1}^{1,1}=0$
by assumption, so
$E_{1}^{0,2}=E_{1}^{1,1}=0$
by assumption, so
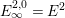 $E_{\infty }^{2,0}=E^{2}$
, and (i) of (2) follows. Note that
$E_{\infty }^{2,0}=E^{2}$
, and (i) of (2) follows. Note that
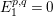 $E_{1}^{p,q}=0$
for
$E_{1}^{p,q}=0$
for
![]() $p\geqslant 3$
. Moreover,
$p\geqslant 3$
. Moreover,
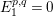 $E_{1}^{p,q}=0$
for
$E_{1}^{p,q}=0$
for
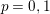 $p=0,1$
and
$p=0,1$
and
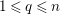 $1\leqslant q\leqslant n$
. So for
$1\leqslant q\leqslant n$
. So for
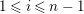 $1\leqslant i\leqslant n-1$
, we have
$1\leqslant i\leqslant n-1$
, we have
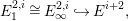 $$\begin{eqnarray}E_{1}^{2,i}\cong E_{\infty }^{2,i}{\hookrightarrow}E^{i+2},\end{eqnarray}$$
$$\begin{eqnarray}E_{1}^{2,i}\cong E_{\infty }^{2,i}{\hookrightarrow}E^{i+2},\end{eqnarray}$$
and the inclusion is an isomorphism if
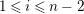 $1\leqslant i\leqslant n-2$
. So (ii) and (iii) of (2) follow.◻
$1\leqslant i\leqslant n-2$
. So (ii) and (iii) of (2) follow.◻
Corollary 4.14. Let
![]() $n\geqslant 1$
. If
$n\geqslant 1$
. If
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
is
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
is
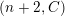 $(n+2,C)$
-TF, then
$(n+2,C)$
-TF, then
![]() $M$
is
$M$
is
![]() $(n,C)$
-TF if and only if
$(n,C)$
-TF if and only if
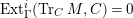 $Ext_{\unicode[STIX]{x1D6E4}}^{i}(Tr_{C}M,C)=0$
for
$Ext_{\unicode[STIX]{x1D6E4}}^{i}(Tr_{C}M,C)=0$
for
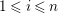 $1\leqslant i\leqslant n$
. If
$1\leqslant i\leqslant n$
. If
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
is
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6EC}}$
is
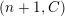 $(n+1,C)$
-TF and
$(n+1,C)$
-TF and
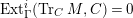 $Ext_{\unicode[STIX]{x1D6E4}}^{i}(Tr_{C}M,C)=0$
for
$Ext_{\unicode[STIX]{x1D6E4}}^{i}(Tr_{C}M,C)=0$
for
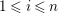 $1\leqslant i\leqslant n$
, then
$1\leqslant i\leqslant n$
, then
![]() $M$
is
$M$
is
![]() $(n,C)$
-TF.
$(n,C)$
-TF.
5 Canonical module
5.1
Let
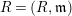 $R=(R,\mathfrak{m})$
be semilocal, where
$R=(R,\mathfrak{m})$
be semilocal, where
![]() $\mathfrak{m}$
is the Jacobson radical of
$\mathfrak{m}$
is the Jacobson radical of
![]() $R$
.
$R$
.
5.2
We say that a dualizing complex
![]() $\mathbb{I}$
over
$\mathbb{I}$
over
![]() $R$
is normalized if for any maximal ideal
$R$
is normalized if for any maximal ideal
![]() $\mathfrak{n}$
of
$\mathfrak{n}$
of
![]() $R$
,
$R$
,
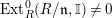 $Ext_{R}^{0}(R/\mathfrak{n},\mathbb{I})\neq 0$
. We follow the definition of [Reference HartshorneHart].
$Ext_{R}^{0}(R/\mathfrak{n},\mathbb{I})\neq 0$
. We follow the definition of [Reference HartshorneHart].
5.3
For a left or right
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() $M$
,
$M$
,
![]() $\dim M$
or
$\dim M$
or
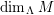 $\dim _{\unicode[STIX]{x1D6EC}}M$
denotes the dimension
$\dim _{\unicode[STIX]{x1D6EC}}M$
denotes the dimension
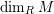 $\dim _{R}M$
of
$\dim _{R}M$
of
![]() $M$
, which is independent of the choice of
$M$
, which is independent of the choice of
![]() $R$
. We call
$R$
. We call
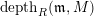 $depth_{R}(\mathfrak{m},M)$
, which is also independent of
$depth_{R}(\mathfrak{m},M)$
, which is also independent of
![]() $R$
, the global depth,
$R$
, the global depth,
![]() $\unicode[STIX]{x1D6EC}$
-depth, or depth of
$\unicode[STIX]{x1D6EC}$
-depth, or depth of
![]() $M$
, and denote it by
$M$
, and denote it by
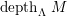 $depth_{\unicode[STIX]{x1D6EC}}M$
or
$depth_{\unicode[STIX]{x1D6EC}}M$
or
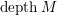 $depthM$
.
$depthM$
.
![]() $M$
is called globally Cohen–Macaulay or GCM for short, if
$M$
is called globally Cohen–Macaulay or GCM for short, if
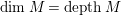 $\dim M= depthM$
.
$\dim M= depthM$
.
![]() $M$
is GCM if and only if it is Cohen–Macaulay as an
$M$
is GCM if and only if it is Cohen–Macaulay as an
![]() $R$
-module, and all the maximal ideals of
$R$
-module, and all the maximal ideals of
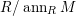 $R/ann_{R}M$
have the same height. This notion is independent of
$R/ann_{R}M$
have the same height. This notion is independent of
![]() $R$
, and depends only on
$R$
, and depends only on
![]() $\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}$
and
![]() $M$
.
$M$
.
![]() $M$
is called a globally maximal Cohen–Macaulay (GMCM for short) if
$M$
is called a globally maximal Cohen–Macaulay (GMCM for short) if
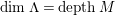 $\dim \unicode[STIX]{x1D6EC}= depthM$
. We say that the algebra
$\dim \unicode[STIX]{x1D6EC}= depthM$
. We say that the algebra
![]() $\unicode[STIX]{x1D6EC}$
is GCM if the
$\unicode[STIX]{x1D6EC}$
is GCM if the
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() $\unicode[STIX]{x1D6EC}$
is GCM. However, in what follows, if
$\unicode[STIX]{x1D6EC}$
is GCM. However, in what follows, if
![]() $R$
happens to be local, then GCM and Cohen–Macaulay (resp. GMSM and maximal Cohen–Macaulay) (over
$R$
happens to be local, then GCM and Cohen–Macaulay (resp. GMSM and maximal Cohen–Macaulay) (over
![]() $R$
) are the same thing, and used interchangeably.
$R$
) are the same thing, and used interchangeably.
5.4
Assume that
![]() $(R,\mathfrak{m})$
is complete semilocal, and
$(R,\mathfrak{m})$
is complete semilocal, and
![]() $\unicode[STIX]{x1D6EC}\neq 0$
. Let
$\unicode[STIX]{x1D6EC}\neq 0$
. Let
![]() $\mathbb{I}$
be a normalized dualizing complex of
$\mathbb{I}$
be a normalized dualizing complex of
![]() $R$
. The lowest nonvanishing cohomology group
$R$
. The lowest nonvanishing cohomology group
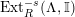 $Ext_{R}^{-s}(\unicode[STIX]{x1D6EC},\mathbb{I})$
(
$Ext_{R}^{-s}(\unicode[STIX]{x1D6EC},\mathbb{I})$
(
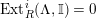 $Ext_{R}^{i}(\unicode[STIX]{x1D6EC},\mathbb{I})=0$
for
$Ext_{R}^{i}(\unicode[STIX]{x1D6EC},\mathbb{I})=0$
for
![]() $i<-s$
) is denoted by
$i<-s$
) is denoted by
![]() $K_{\unicode[STIX]{x1D6EC}}$
, and is called the canonical module of
$K_{\unicode[STIX]{x1D6EC}}$
, and is called the canonical module of
![]() $\unicode[STIX]{x1D6EC}$
. Note that
$\unicode[STIX]{x1D6EC}$
. Note that
![]() $K_{\unicode[STIX]{x1D6EC}}$
is a
$K_{\unicode[STIX]{x1D6EC}}$
is a
![]() $\unicode[STIX]{x1D6EC}$
-bimodule. Hence it is also a
$\unicode[STIX]{x1D6EC}$
-bimodule. Hence it is also a
![]() $\unicode[STIX]{x1D6EC}^{op}$
-bimodule. In this sense,
$\unicode[STIX]{x1D6EC}^{op}$
-bimodule. In this sense,
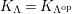 $K_{\unicode[STIX]{x1D6EC}}=K_{\unicode[STIX]{x1D6EC}^{op}}$
. If
$K_{\unicode[STIX]{x1D6EC}}=K_{\unicode[STIX]{x1D6EC}^{op}}$
. If
![]() $\unicode[STIX]{x1D6EC}=0$
, then we define
$\unicode[STIX]{x1D6EC}=0$
, then we define
![]() $K_{\unicode[STIX]{x1D6EC}}=0$
.
$K_{\unicode[STIX]{x1D6EC}}=0$
.
5.5
Let
![]() $S$
be the center of
$S$
be the center of
![]() $\unicode[STIX]{x1D6EC}$
. Then
$\unicode[STIX]{x1D6EC}$
. Then
![]() $S$
is module-finite over
$S$
is module-finite over
![]() $R$
, and
$R$
, and
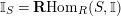 $\mathbb{I}_{S}=\mathbf{R}\text{Hom}_{R}(S,\mathbb{I})$
is a normalized dualizing complex of
$\mathbb{I}_{S}=\mathbf{R}\text{Hom}_{R}(S,\mathbb{I})$
is a normalized dualizing complex of
![]() $S$
. This shows that
$S$
. This shows that
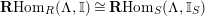 $\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})\cong \mathbf{R}\text{Hom}_{S}(\unicode[STIX]{x1D6EC},\mathbb{I}_{S})$
, and hence the definition of
$\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})\cong \mathbf{R}\text{Hom}_{S}(\unicode[STIX]{x1D6EC},\mathbb{I}_{S})$
, and hence the definition of
![]() $K_{\unicode[STIX]{x1D6EC}}$
is also independent of
$K_{\unicode[STIX]{x1D6EC}}$
is also independent of
![]() $R$
.
$R$
.
Lemma 5.6. The number
![]() $s$
in (5.4) is nothing but
$s$
in (5.4) is nothing but
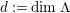 $d:=\dim \unicode[STIX]{x1D6EC}$
. Moreover,
$d:=\dim \unicode[STIX]{x1D6EC}$
. Moreover,
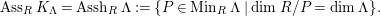 $$\begin{eqnarray}Ass_{R}K_{\unicode[STIX]{x1D6EC}}= Assh_{R}\unicode[STIX]{x1D6EC}:=\{P\in Min_{R}\unicode[STIX]{x1D6EC}\mid \dim R/P=\dim \unicode[STIX]{x1D6EC}\}.\end{eqnarray}$$
$$\begin{eqnarray}Ass_{R}K_{\unicode[STIX]{x1D6EC}}= Assh_{R}\unicode[STIX]{x1D6EC}:=\{P\in Min_{R}\unicode[STIX]{x1D6EC}\mid \dim R/P=\dim \unicode[STIX]{x1D6EC}\}.\end{eqnarray}$$
Proof. We may replace
![]() $R$
by
$R$
by
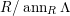 $R/ann_{R}\unicode[STIX]{x1D6EC}$
, and may assume that
$R/ann_{R}\unicode[STIX]{x1D6EC}$
, and may assume that
![]() $\unicode[STIX]{x1D6EC}$
is a faithful module. We may assume that
$\unicode[STIX]{x1D6EC}$
is a faithful module. We may assume that
![]() $\mathbb{I}$
is a fundamental dualizing complex of
$\mathbb{I}$
is a fundamental dualizing complex of
![]() $R$
. That is, for each
$R$
. That is, for each
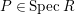 $P\in SpecR$
,
$P\in SpecR$
,
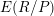 $E(R/P)$
, the injective hull of
$E(R/P)$
, the injective hull of
![]() $R/P$
, appears exactly once (at dimension
$R/P$
, appears exactly once (at dimension
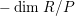 $-\dim R/P$
). If
$-\dim R/P$
). If
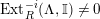 $Ext_{R}^{-i}(\unicode[STIX]{x1D6EC},\mathbb{I})\neq 0$
, then there exists some
$Ext_{R}^{-i}(\unicode[STIX]{x1D6EC},\mathbb{I})\neq 0$
, then there exists some
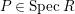 $P\in SpecR$
such that
$P\in SpecR$
such that
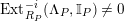 $Ext_{R_{P}}^{-i}(\unicode[STIX]{x1D6EC}_{P},\mathbb{I}_{P})\neq 0$
. Then
$Ext_{R_{P}}^{-i}(\unicode[STIX]{x1D6EC}_{P},\mathbb{I}_{P})\neq 0$
. Then
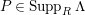 $P\in Supp_{R}\unicode[STIX]{x1D6EC}$
and
$P\in Supp_{R}\unicode[STIX]{x1D6EC}$
and
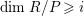 $\dim R/P\geqslant i$
. On the other hand,
$\dim R/P\geqslant i$
. On the other hand,
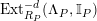 $Ext_{R_{P}}^{-d}(\unicode[STIX]{x1D6EC}_{P},\mathbb{I}_{P})$
has length
$Ext_{R_{P}}^{-d}(\unicode[STIX]{x1D6EC}_{P},\mathbb{I}_{P})$
has length
![]() $l(\unicode[STIX]{x1D6EC}_{P})$
and is nonzero for
$l(\unicode[STIX]{x1D6EC}_{P})$
and is nonzero for
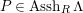 $P\in Assh_{R}\unicode[STIX]{x1D6EC}$
. So
$P\in Assh_{R}\unicode[STIX]{x1D6EC}$
. So
![]() $s=d$
.
$s=d$
.
The argument above shows that each
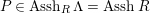 $P\in Assh_{R}\unicode[STIX]{x1D6EC}= AsshR$
supports
$P\in Assh_{R}\unicode[STIX]{x1D6EC}= AsshR$
supports
![]() $K_{\unicode[STIX]{x1D6EC}}$
. So
$K_{\unicode[STIX]{x1D6EC}}$
. So
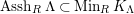 $Assh_{R}\unicode[STIX]{x1D6EC}\subset Min_{R}K_{\unicode[STIX]{x1D6EC}}$
. On the other hand, as the complex
$Assh_{R}\unicode[STIX]{x1D6EC}\subset Min_{R}K_{\unicode[STIX]{x1D6EC}}$
. On the other hand, as the complex
![]() $\mathbb{I}$
starts at degree
$\mathbb{I}$
starts at degree
![]() $-d$
,
$-d$
,
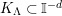 $K_{\unicode[STIX]{x1D6EC}}\subset \mathbb{I}^{-d}$
, and
$K_{\unicode[STIX]{x1D6EC}}\subset \mathbb{I}^{-d}$
, and
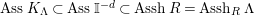 $AssK_{\unicode[STIX]{x1D6EC}}\subset Ass\mathbb{I}^{-d}\subset AsshR= Assh_{R}\unicode[STIX]{x1D6EC}$
.◻
$AssK_{\unicode[STIX]{x1D6EC}}\subset Ass\mathbb{I}^{-d}\subset AsshR= Assh_{R}\unicode[STIX]{x1D6EC}$
.◻
Lemma 5.7. Let
![]() $(R,\mathfrak{m})$
be complete semilocal. Then
$(R,\mathfrak{m})$
be complete semilocal. Then
![]() $K_{\unicode[STIX]{x1D6EC}}$
satisfies the
$K_{\unicode[STIX]{x1D6EC}}$
satisfies the
![]() $(S_{2}^{\unicode[STIX]{x1D6EC}})^{R}$
-condition.
$(S_{2}^{\unicode[STIX]{x1D6EC}})^{R}$
-condition.
Proof. It is easy to see that
![]() $(K_{\unicode[STIX]{x1D6EC}})_{\mathfrak{n}}$
is either zero or
$(K_{\unicode[STIX]{x1D6EC}})_{\mathfrak{n}}$
is either zero or
![]() $K_{\unicode[STIX]{x1D6EC}_{\mathfrak{n}}}$
for each maximal ideal
$K_{\unicode[STIX]{x1D6EC}_{\mathfrak{n}}}$
for each maximal ideal
![]() $\mathfrak{n}$
of
$\mathfrak{n}$
of
![]() $R$
. Hence we may assume that
$R$
. Hence we may assume that
![]() $R$
is local. Replacing
$R$
is local. Replacing
![]() $R$
by
$R$
by
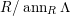 $R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
$R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
![]() $\unicode[STIX]{x1D6EC}$
is a faithful
$\unicode[STIX]{x1D6EC}$
is a faithful
![]() $R$
-module, and we are to prove that
$R$
-module, and we are to prove that
![]() $K_{\unicode[STIX]{x1D6EC}}$
satisfies
$K_{\unicode[STIX]{x1D6EC}}$
satisfies
![]() $(S_{2}^{\prime })^{R}$
by Lemma 2.18. Replacing
$(S_{2}^{\prime })^{R}$
by Lemma 2.18. Replacing
![]() $R$
by a Noether normalization, we may further assume that
$R$
by a Noether normalization, we may further assume that
![]() $R$
is regular by Lemma 2.20(1). Then
$R$
is regular by Lemma 2.20(1). Then
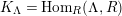 $K_{\unicode[STIX]{x1D6EC}}= Hom_{R}(\unicode[STIX]{x1D6EC},R)$
. So
$K_{\unicode[STIX]{x1D6EC}}= Hom_{R}(\unicode[STIX]{x1D6EC},R)$
. So
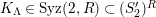 $K_{\unicode[STIX]{x1D6EC}}\in Syz(2,R)\subset (S_{2}^{\prime })^{R}$
by Lemma 4.8 (consider that
$K_{\unicode[STIX]{x1D6EC}}\in Syz(2,R)\subset (S_{2}^{\prime })^{R}$
by Lemma 4.8 (consider that
![]() $\unicode[STIX]{x1D6EC}$
there is
$\unicode[STIX]{x1D6EC}$
there is
![]() $R$
here, and
$R$
here, and
![]() $C$
there is also
$C$
there is also
![]() $R$
here).◻
$R$
here).◻
5.8
Assume that
![]() $(R,\mathfrak{m})$
is semilocal which need not be complete. We say that a finitely generated
$(R,\mathfrak{m})$
is semilocal which need not be complete. We say that a finitely generated
![]() $\unicode[STIX]{x1D6EC}$
-bimodule
$\unicode[STIX]{x1D6EC}$
-bimodule
![]() $K$
is a canonical module of
$K$
is a canonical module of
![]() $\unicode[STIX]{x1D6EC}$
if
$\unicode[STIX]{x1D6EC}$
if
![]() $\hat{K}$
is isomorphic to the canonical module
$\hat{K}$
is isomorphic to the canonical module
![]() $K_{\hat{\unicode[STIX]{x1D6EC}}}$
as a
$K_{\hat{\unicode[STIX]{x1D6EC}}}$
as a
![]() $\hat{\unicode[STIX]{x1D6EC}}$
-bimodule, where
$\hat{\unicode[STIX]{x1D6EC}}$
-bimodule, where
![]() $\hat{?}$
denotes the
$\hat{?}$
denotes the
![]() $\mathfrak{m}$
-adic completion. It is unique up to isomorphisms, and denoted by
$\mathfrak{m}$
-adic completion. It is unique up to isomorphisms, and denoted by
![]() $K_{\unicode[STIX]{x1D6EC}}$
. We say that
$K_{\unicode[STIX]{x1D6EC}}$
. We say that
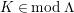 $K\in mod\unicode[STIX]{x1D6EC}$
is a right canonical module of
$K\in mod\unicode[STIX]{x1D6EC}$
is a right canonical module of
![]() $\unicode[STIX]{x1D6EC}$
if
$\unicode[STIX]{x1D6EC}$
if
![]() $\hat{K}$
is isomorphic to
$\hat{K}$
is isomorphic to
![]() $K_{\hat{\unicode[STIX]{x1D6EC}}}$
in
$K_{\hat{\unicode[STIX]{x1D6EC}}}$
in
![]() ${\rm mod}\hat{\unicode[STIX]{x1D6EC}}$
. If
${\rm mod}\hat{\unicode[STIX]{x1D6EC}}$
. If
![]() $K_{\unicode[STIX]{x1D6EC}}$
exists, then
$K_{\unicode[STIX]{x1D6EC}}$
exists, then
![]() $K$
is a right canonical module if and only if
$K$
is a right canonical module if and only if
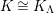 $K\cong K_{\unicode[STIX]{x1D6EC}}$
in
$K\cong K_{\unicode[STIX]{x1D6EC}}$
in
![]() ${\rm mod}\unicode[STIX]{x1D6EC}$
.
${\rm mod}\unicode[STIX]{x1D6EC}$
.
These definitions are independent of
![]() $R$
, in the sense that the (right) canonical module over
$R$
, in the sense that the (right) canonical module over
![]() $R$
and that over the center of
$R$
and that over the center of
![]() $\unicode[STIX]{x1D6EC}$
are the same thing. The right canonical module of
$\unicode[STIX]{x1D6EC}$
are the same thing. The right canonical module of
![]() $\unicode[STIX]{x1D6EC}^{op}$
is called the left canonical module. A
$\unicode[STIX]{x1D6EC}^{op}$
is called the left canonical module. A
![]() $\unicode[STIX]{x1D6EC}$
-bimodule
$\unicode[STIX]{x1D6EC}$
-bimodule
![]() $\unicode[STIX]{x1D714}$
is said to be a weakly canonical bimodule if
$\unicode[STIX]{x1D714}$
is said to be a weakly canonical bimodule if
![]() $_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D714}$
is left canonical, and
$_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D714}$
is left canonical, and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}$
is right canonical. The canonical module
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6EC}}$
is right canonical. The canonical module
![]() $K_{\unicode[STIX]{x1D6EC}^{op}}$
of
$K_{\unicode[STIX]{x1D6EC}^{op}}$
of
![]() $\unicode[STIX]{x1D6EC}^{op}$
is canonically identified with
$\unicode[STIX]{x1D6EC}^{op}$
is canonically identified with
![]() $K_{\unicode[STIX]{x1D6EC}}$
.
$K_{\unicode[STIX]{x1D6EC}}$
.
5.9
If
![]() $R$
has a normalized dualizing complex
$R$
has a normalized dualizing complex
![]() $\mathbb{I}$
, then
$\mathbb{I}$
, then
![]() $\hat{\mathbb{I}}$
is a normalized dualizing complex of
$\hat{\mathbb{I}}$
is a normalized dualizing complex of
![]() $\hat{R}$
, and so it is easy to see that
$\hat{R}$
, and so it is easy to see that
![]() $K_{\unicode[STIX]{x1D6EC}}$
exists and agrees with
$K_{\unicode[STIX]{x1D6EC}}$
exists and agrees with
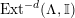 $Ext^{-d}(\unicode[STIX]{x1D6EC},\mathbb{I})$
, where
$Ext^{-d}(\unicode[STIX]{x1D6EC},\mathbb{I})$
, where
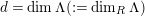 $d=\dim \unicode[STIX]{x1D6EC}(:=\dim _{R}\unicode[STIX]{x1D6EC})$
. In this case, for any
$d=\dim \unicode[STIX]{x1D6EC}(:=\dim _{R}\unicode[STIX]{x1D6EC})$
. In this case, for any
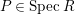 $P\in SpecR$
,
$P\in SpecR$
,
![]() $\mathbb{I}_{P}$
is a dualizing complex of
$\mathbb{I}_{P}$
is a dualizing complex of
![]() $R_{P}$
. So if
$R_{P}$
. So if
![]() $R$
has a dualizing complex and
$R$
has a dualizing complex and
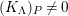 $(K_{\unicode[STIX]{x1D6EC}})_{P}\neq 0$
, then
$(K_{\unicode[STIX]{x1D6EC}})_{P}\neq 0$
, then
![]() $(K_{\unicode[STIX]{x1D6EC}})_{P}$
, which is the lowest nonzero cohomology group of
$(K_{\unicode[STIX]{x1D6EC}})_{P}$
, which is the lowest nonzero cohomology group of
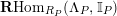 $\mathbf{R}\text{Hom}_{R_{P}}(\unicode[STIX]{x1D6EC}_{P},\mathbb{I}_{P})$
, is the
$\mathbf{R}\text{Hom}_{R_{P}}(\unicode[STIX]{x1D6EC}_{P},\mathbb{I}_{P})$
, is the
![]() $R_{P}$
-canonical module of
$R_{P}$
-canonical module of
![]() $\unicode[STIX]{x1D6EC}_{P}$
. See also Theorem 7.5 below.
$\unicode[STIX]{x1D6EC}_{P}$
. See also Theorem 7.5 below.
Lemma 5.10. Let
![]() $(R,\mathfrak{m})$
be local, and assume that
$(R,\mathfrak{m})$
be local, and assume that
![]() $K_{\unicode[STIX]{x1D6EC}}$
exists. Then we have the following.
$K_{\unicode[STIX]{x1D6EC}}$
exists. Then we have the following.
-
(1)
 $Ass_{R}K_{\unicode[STIX]{x1D6EC}}= Assh_{R}\unicode[STIX]{x1D6EC}$
.
$Ass_{R}K_{\unicode[STIX]{x1D6EC}}= Assh_{R}\unicode[STIX]{x1D6EC}$
. -
(2)
 $K_{\unicode[STIX]{x1D6EC}}\in (S_{2}^{\unicode[STIX]{x1D6EC}})^{R}$
.
$K_{\unicode[STIX]{x1D6EC}}\in (S_{2}^{\unicode[STIX]{x1D6EC}})^{R}$
. -
(3)
 $R/annK_{\unicode[STIX]{x1D6EC}}$
is quasi-unmixed, and hence is universally catenary.
$R/annK_{\unicode[STIX]{x1D6EC}}$
is quasi-unmixed, and hence is universally catenary.
Proof. All the assertions are proved easily using the case that
![]() $R$
is complete.◻
$R$
is complete.◻
5.11
A
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() $M$
is said to be
$M$
is said to be
![]() $\unicode[STIX]{x1D6EC}$
-full over
$\unicode[STIX]{x1D6EC}$
-full over
![]() $R$
if
$R$
if
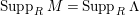 $Supp_{R}M= Supp_{R}\unicode[STIX]{x1D6EC}$
.
$Supp_{R}M= Supp_{R}\unicode[STIX]{x1D6EC}$
.
Lemma 5.12. Let
![]() $(R,\mathfrak{m})$
be local. If
$(R,\mathfrak{m})$
be local. If
![]() $K_{\unicode[STIX]{x1D6EC}}$
exists and
$K_{\unicode[STIX]{x1D6EC}}$
exists and
![]() $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
![]() $(S_{2})^{R}$
-condition, then
$(S_{2})^{R}$
-condition, then
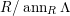 $R/ann_{R}\unicode[STIX]{x1D6EC}$
is equidimensional, and
$R/ann_{R}\unicode[STIX]{x1D6EC}$
is equidimensional, and
![]() $K_{\unicode[STIX]{x1D6EC}}$
is
$K_{\unicode[STIX]{x1D6EC}}$
is
![]() $\unicode[STIX]{x1D6EC}$
-full over
$\unicode[STIX]{x1D6EC}$
-full over
![]() $R$
.
$R$
.
Proof. The same as the proof of [Reference OgomaOgo, Lemma 4.1] (use Lemma 5.10(3)). ◻
5.13
Let
![]() $(R,\mathfrak{m})$
be local, and
$(R,\mathfrak{m})$
be local, and
![]() $\mathbb{I}$
be a normalized dualizing complex. By the local duality,
$\mathbb{I}$
be a normalized dualizing complex. By the local duality,
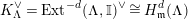 $$\begin{eqnarray}K_{\unicode[STIX]{x1D6EC}}^{\vee }= Ext^{-d}(\unicode[STIX]{x1D6EC},\mathbb{I})^{\vee }\cong H_{\mathfrak{ m}}^{d}(\unicode[STIX]{x1D6EC})\end{eqnarray}$$
$$\begin{eqnarray}K_{\unicode[STIX]{x1D6EC}}^{\vee }= Ext^{-d}(\unicode[STIX]{x1D6EC},\mathbb{I})^{\vee }\cong H_{\mathfrak{ m}}^{d}(\unicode[STIX]{x1D6EC})\end{eqnarray}$$
(as
![]() $\unicode[STIX]{x1D6EC}$
-bimodules), where
$\unicode[STIX]{x1D6EC}$
-bimodules), where
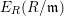 $E_{R}(R/\mathfrak{m})$
is the injective hull of the
$E_{R}(R/\mathfrak{m})$
is the injective hull of the
![]() $R$
-module
$R$
-module
![]() $R/\mathfrak{m}$
, and
$R/\mathfrak{m}$
, and
![]() $(?)^{\vee }$
is the Matlis dual
$(?)^{\vee }$
is the Matlis dual
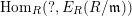 $Hom_{R}(?,E_{R}(R/\mathfrak{m}))$
.
$Hom_{R}(?,E_{R}(R/\mathfrak{m}))$
.
5.14
Let
![]() $(R,\mathfrak{m})$
be semilocal, and
$(R,\mathfrak{m})$
be semilocal, and
![]() $\mathbb{I}$
be a normalized dualizing complex. Note that
$\mathbb{I}$
be a normalized dualizing complex. Note that
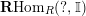 $\mathbf{R}\text{Hom}_{R}(?,\mathbb{I})$
induces a contravariant equivalence between
$\mathbf{R}\text{Hom}_{R}(?,\mathbb{I})$
induces a contravariant equivalence between
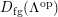 $D_{fg}(\unicode[STIX]{x1D6EC}^{op})$
and
$D_{fg}(\unicode[STIX]{x1D6EC}^{op})$
and
![]() $D_{fg}(\unicode[STIX]{x1D6EC})$
. Let
$D_{fg}(\unicode[STIX]{x1D6EC})$
. Let
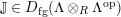 $\mathbb{J}\in D_{fg}(\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op})$
be
$\mathbb{J}\in D_{fg}(\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op})$
be
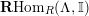 $\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
.
$\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
.
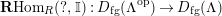 $$\begin{eqnarray}\mathbf{R}\text{Hom}_{R}(?,\mathbb{I}):D_{fg}(\unicode[STIX]{x1D6EC}^{op})\rightarrow D_{ fg}(\unicode[STIX]{x1D6EC})\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{R}\text{Hom}_{R}(?,\mathbb{I}):D_{fg}(\unicode[STIX]{x1D6EC}^{op})\rightarrow D_{ fg}(\unicode[STIX]{x1D6EC})\end{eqnarray}$$
is identified with
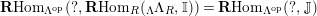 $$\begin{eqnarray}\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(?,\mathbf{R}\text{Hom}_{R}(\text{}_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}_{R},\mathbb{I}))=\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(?,\mathbb{J})\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(?,\mathbf{R}\text{Hom}_{R}(\text{}_{\unicode[STIX]{x1D6EC}}\unicode[STIX]{x1D6EC}_{R},\mathbb{I}))=\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(?,\mathbb{J})\end{eqnarray}$$
and similarly,
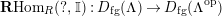 $$\begin{eqnarray}\mathbf{R}\text{Hom}_{R}(?,\mathbb{I}):D_{fg}(\unicode[STIX]{x1D6EC})\rightarrow D_{fg}(\unicode[STIX]{x1D6EC}^{op})\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{R}\text{Hom}_{R}(?,\mathbb{I}):D_{fg}(\unicode[STIX]{x1D6EC})\rightarrow D_{fg}(\unicode[STIX]{x1D6EC}^{op})\end{eqnarray}$$
is identified with
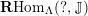 $\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}}(?,\mathbb{J})$
. Note that a left or right
$\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}}(?,\mathbb{J})$
. Note that a left or right
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
![]() $M$
is GMCM if and only if
$M$
is GMCM if and only if
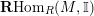 $\mathbf{R}\text{Hom}_{R}(M,\mathbb{I})$
is concentrated in degree
$\mathbf{R}\text{Hom}_{R}(M,\mathbb{I})$
is concentrated in degree
![]() $-d$
, where
$-d$
, where
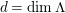 $d=\dim \unicode[STIX]{x1D6EC}$
.
$d=\dim \unicode[STIX]{x1D6EC}$
.
5.15
![]() $\mathbb{J}$
above is a dualizing complex of
$\mathbb{J}$
above is a dualizing complex of
![]() $\unicode[STIX]{x1D6EC}$
in the sense of Yekutieli [Reference YekutieliYek, (3.3)].
$\unicode[STIX]{x1D6EC}$
in the sense of Yekutieli [Reference YekutieliYek, (3.3)].
5.16
![]() $\unicode[STIX]{x1D6EC}$
is GCM if and only if
$\unicode[STIX]{x1D6EC}$
is GCM if and only if
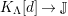 $K_{\unicode[STIX]{x1D6EC}}[d]\rightarrow \mathbb{J}$
is an isomorphism. If so,
$K_{\unicode[STIX]{x1D6EC}}[d]\rightarrow \mathbb{J}$
is an isomorphism. If so,
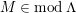 $M\in mod\unicode[STIX]{x1D6EC}$
is GMCM if and only if
$M\in mod\unicode[STIX]{x1D6EC}$
is GMCM if and only if
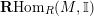 $\mathbf{R}\text{Hom}_{R}(M,\mathbb{I})$
is concentrated in degree
$\mathbf{R}\text{Hom}_{R}(M,\mathbb{I})$
is concentrated in degree
![]() $-d$
if and only if
$-d$
if and only if
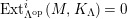 $Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(M,K_{\unicode[STIX]{x1D6EC}})=0$
for
$Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(M,K_{\unicode[STIX]{x1D6EC}})=0$
for
![]() $i>0$
. Also, in this case, as
$i>0$
. Also, in this case, as
![]() $K_{\unicode[STIX]{x1D6EC}}[d]$
is a dualizing complex, it is of finite injective dimension both as a left and a right
$K_{\unicode[STIX]{x1D6EC}}[d]$
is a dualizing complex, it is of finite injective dimension both as a left and a right
![]() $\unicode[STIX]{x1D6EC}$
-module. To prove these, we may take the completion, and may assume that
$\unicode[STIX]{x1D6EC}$
-module. To prove these, we may take the completion, and may assume that
![]() $R$
is complete. All the assertions are independent of
$R$
is complete. All the assertions are independent of
![]() $R$
, so taking the Noether normalization, we may assume that
$R$
, so taking the Noether normalization, we may assume that
![]() $R$
is local. By (5.14), the assertions follow.
$R$
is local. By (5.14), the assertions follow.
5.17
For any
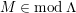 $M\in mod\unicode[STIX]{x1D6EC}$
which is GMCM,
$M\in mod\unicode[STIX]{x1D6EC}$
which is GMCM,
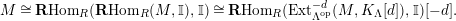 $$\begin{eqnarray}M\cong \mathbf{R}\text{Hom}_{R}(\mathbf{R}\text{Hom}_{R}(M,\mathbb{I}),\mathbb{I})\cong \mathbf{R}\text{Hom}_{R}(Ext_{\unicode[STIX]{x1D6EC}^{op}}^{-d}(M,K_{\unicode[STIX]{x1D6EC}}[d]),\mathbb{I})[-d].\end{eqnarray}$$
$$\begin{eqnarray}M\cong \mathbf{R}\text{Hom}_{R}(\mathbf{R}\text{Hom}_{R}(M,\mathbb{I}),\mathbb{I})\cong \mathbf{R}\text{Hom}_{R}(Ext_{\unicode[STIX]{x1D6EC}^{op}}^{-d}(M,K_{\unicode[STIX]{x1D6EC}}[d]),\mathbb{I})[-d].\end{eqnarray}$$
Hence
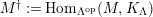 $M^{\dagger }:= Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,K_{\unicode[STIX]{x1D6EC}})$
is also a GMCM
$M^{\dagger }:= Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,K_{\unicode[STIX]{x1D6EC}})$
is also a GMCM
![]() $\unicode[STIX]{x1D6EC}$
-module, and hence
$\unicode[STIX]{x1D6EC}$
-module, and hence
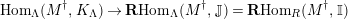 $$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6EC}}(M^{\dagger },K_{\unicode[STIX]{x1D6EC}})\rightarrow \mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}}(M^{\dagger },\mathbb{J})=\mathbf{R}\text{Hom}_{R}(M^{\dagger },\mathbb{I})\end{eqnarray}$$
$$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6EC}}(M^{\dagger },K_{\unicode[STIX]{x1D6EC}})\rightarrow \mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}}(M^{\dagger },\mathbb{J})=\mathbf{R}\text{Hom}_{R}(M^{\dagger },\mathbb{I})\end{eqnarray}$$
is an isomorphism (in other words,
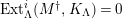 $Ext_{\unicode[STIX]{x1D6EC}}^{i}(M^{\dagger },K_{\unicode[STIX]{x1D6EC}})=0$
for
$Ext_{\unicode[STIX]{x1D6EC}}^{i}(M^{\dagger },K_{\unicode[STIX]{x1D6EC}})=0$
for
![]() $i>0$
). So the canonical map
$i>0$
). So the canonical map
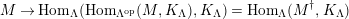 $$\begin{eqnarray}M\rightarrow Hom_{\unicode[STIX]{x1D6EC}}(Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,K_{\unicode[STIX]{x1D6EC}}),K_{\unicode[STIX]{x1D6EC}})= Hom_{\unicode[STIX]{x1D6EC}}(M^{\dagger },K_{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$
$$\begin{eqnarray}M\rightarrow Hom_{\unicode[STIX]{x1D6EC}}(Hom_{\unicode[STIX]{x1D6EC}^{op}}(M,K_{\unicode[STIX]{x1D6EC}}),K_{\unicode[STIX]{x1D6EC}})= Hom_{\unicode[STIX]{x1D6EC}}(M^{\dagger },K_{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$
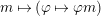 $m\mapsto (\unicode[STIX]{x1D711}\mapsto \unicode[STIX]{x1D711}m)$
is an isomorphism. This isomorphism is true without assuming that
$m\mapsto (\unicode[STIX]{x1D711}\mapsto \unicode[STIX]{x1D711}m)$
is an isomorphism. This isomorphism is true without assuming that
![]() $R$
has a dualizing complex (but assuming the existence of a canonical module), passing to the completion. Note that if
$R$
has a dualizing complex (but assuming the existence of a canonical module), passing to the completion. Note that if
![]() $\unicode[STIX]{x1D6EC}=R$
,
$\unicode[STIX]{x1D6EC}=R$
,
![]() $K_{R}$
exists, and
$K_{R}$
exists, and
![]() $R$
is Cohen–Macaulay, then
$R$
is Cohen–Macaulay, then
![]() $K_{R}$
is a dualizing complex of
$K_{R}$
is a dualizing complex of
![]() $R$
.
$R$
.
Similarly, for
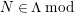 $N\in \unicode[STIX]{x1D6EC}{\rm mod}$
which is GMCM,
$N\in \unicode[STIX]{x1D6EC}{\rm mod}$
which is GMCM,
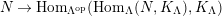 $$\begin{eqnarray}N\rightarrow Hom_{\unicode[STIX]{x1D6EC}^{op}}(Hom_{\unicode[STIX]{x1D6EC}}(N,K_{\unicode[STIX]{x1D6EC}}),K_{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$
$$\begin{eqnarray}N\rightarrow Hom_{\unicode[STIX]{x1D6EC}^{op}}(Hom_{\unicode[STIX]{x1D6EC}}(N,K_{\unicode[STIX]{x1D6EC}}),K_{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$
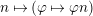 $n\mapsto (\unicode[STIX]{x1D711}\mapsto \unicode[STIX]{x1D711}n)$
is an isomorphism.
$n\mapsto (\unicode[STIX]{x1D711}\mapsto \unicode[STIX]{x1D711}n)$
is an isomorphism.
5.18
In particular, letting
![]() $M=\unicode[STIX]{x1D6EC}$
, if
$M=\unicode[STIX]{x1D6EC}$
, if
![]() $\unicode[STIX]{x1D6EC}$
is GCM, we have that
$\unicode[STIX]{x1D6EC}$
is GCM, we have that
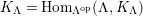 $K_{\unicode[STIX]{x1D6EC}}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},K_{\unicode[STIX]{x1D6EC}})$
is GMCM. Moreover,
$K_{\unicode[STIX]{x1D6EC}}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},K_{\unicode[STIX]{x1D6EC}})$
is GMCM. Moreover,
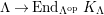 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
is an
![]() $R$
-algebra isomorphism, where
$R$
-algebra isomorphism, where
![]() $a\in \unicode[STIX]{x1D6EC}$
goes to the left multiplication by
$a\in \unicode[STIX]{x1D6EC}$
goes to the left multiplication by
![]() $a$
. Similarly,
$a$
. Similarly,
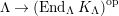 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\rightarrow (End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\rightarrow (End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}\end{eqnarray}$$
is an isomorphism of
![]() $R$
-algebras.
$R$
-algebras.
5.19
Let
![]() $(R,\mathfrak{m})$
be a
$(R,\mathfrak{m})$
be a
![]() $d$
-dimensional complete local ring, and
$d$
-dimensional complete local ring, and
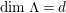 $\dim \unicode[STIX]{x1D6EC}=d$
. Then by the local duality,
$\dim \unicode[STIX]{x1D6EC}=d$
. Then by the local duality,
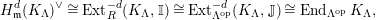 $$\begin{eqnarray}H_{\mathfrak{m}}^{d}(K_{\unicode[STIX]{x1D6EC}})^{\vee }\cong Ext_{R}^{-d}(K_{\unicode[STIX]{x1D6EC}},\mathbb{I})\cong Ext_{\unicode[STIX]{x1D6EC}^{op}}^{-d}(K_{\unicode[STIX]{x1D6EC}},\mathbb{J})\cong End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathfrak{m}}^{d}(K_{\unicode[STIX]{x1D6EC}})^{\vee }\cong Ext_{R}^{-d}(K_{\unicode[STIX]{x1D6EC}},\mathbb{I})\cong Ext_{\unicode[STIX]{x1D6EC}^{op}}^{-d}(K_{\unicode[STIX]{x1D6EC}},\mathbb{J})\cong End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
where
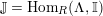 $\mathbb{J}= Hom_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
and
$\mathbb{J}= Hom_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
and
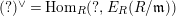 $(?)^{\vee }= Hom_{R}(?,E_{R}(R/\mathfrak{m}))$
.
$(?)^{\vee }= Hom_{R}(?,E_{R}(R/\mathfrak{m}))$
.
6
 $n$
-canonical module
$n$
-canonical module
6.1
We say that
![]() $\unicode[STIX]{x1D714}$
is an
$\unicode[STIX]{x1D714}$
is an
![]() $R$
-semicanonical right
$R$
-semicanonical right
![]() $\unicode[STIX]{x1D6EC}$
-module (resp.
$\unicode[STIX]{x1D6EC}$
-module (resp.
![]() $R$
-semicanonical left
$R$
-semicanonical left
![]() $\unicode[STIX]{x1D6EC}$
-module, weakly
$\unicode[STIX]{x1D6EC}$
-module, weakly
![]() $R$
-semicanonical
$R$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule,
$\unicode[STIX]{x1D6EC}$
-bimodule,
![]() $R$
-semicanonical
$R$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule) if for any
$\unicode[STIX]{x1D6EC}$
-bimodule) if for any
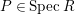 $P\in SpecR$
,
$P\in SpecR$
,
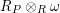 $R_{P}\otimes _{R}\unicode[STIX]{x1D714}$
is the right canonical module (resp. left canonical module, weakly canonical module, canonical module) of
$R_{P}\otimes _{R}\unicode[STIX]{x1D714}$
is the right canonical module (resp. left canonical module, weakly canonical module, canonical module) of
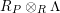 $R_{P}\otimes _{R}\unicode[STIX]{x1D6EC}$
for any
$R_{P}\otimes _{R}\unicode[STIX]{x1D6EC}$
for any
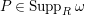 $P\in Supp_{R}\unicode[STIX]{x1D714}$
. If we do not mention what
$P\in Supp_{R}\unicode[STIX]{x1D714}$
. If we do not mention what
![]() $R$
is, then one may take
$R$
is, then one may take
![]() $R$
to be the center of
$R$
to be the center of
![]() $\unicode[STIX]{x1D6EC}$
. An
$\unicode[STIX]{x1D6EC}$
. An
![]() $R$
-semicanonical right
$R$
-semicanonical right
![]() $\unicode[STIX]{x1D6EC}^{op}$
-module (resp.
$\unicode[STIX]{x1D6EC}^{op}$
-module (resp.
![]() $R$
-semicanonical left
$R$
-semicanonical left
![]() $\unicode[STIX]{x1D6EC}^{op}$
-module, weakly
$\unicode[STIX]{x1D6EC}^{op}$
-module, weakly
![]() $R$
-semicanonical
$R$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}^{op}$
-bimodule,
$\unicode[STIX]{x1D6EC}^{op}$
-bimodule,
![]() $R$
-semicanonical
$R$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}^{op}$
-bimodule) is nothing but an
$\unicode[STIX]{x1D6EC}^{op}$
-bimodule) is nothing but an
![]() $R$
-semicanonical left
$R$
-semicanonical left
![]() $\unicode[STIX]{x1D6EC}$
-module (resp.
$\unicode[STIX]{x1D6EC}$
-module (resp.
![]() $R$
-semicanonical right
$R$
-semicanonical right
![]() $\unicode[STIX]{x1D6EC}$
-module, weakly
$\unicode[STIX]{x1D6EC}$
-module, weakly
![]() $R$
-semicanonical
$R$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule,
$\unicode[STIX]{x1D6EC}$
-bimodule,
![]() $R$
-semicanonical
$R$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule).
$\unicode[STIX]{x1D6EC}$
-bimodule).
6.2
Let
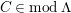 $C\in mod\unicode[STIX]{x1D6EC}$
(resp.
$C\in mod\unicode[STIX]{x1D6EC}$
(resp.
![]() $\unicode[STIX]{x1D6EC}{\rm mod}$
,
$\unicode[STIX]{x1D6EC}{\rm mod}$
,
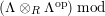 $(\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}){\rm mod}$
,
$(\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}){\rm mod}$
,
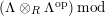 $(\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}){\rm mod}$
). We say that
$(\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}){\rm mod}$
). We say that
![]() $C$
is an
$C$
is an
![]() $n$
-canonical right
$n$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module (resp.
$\unicode[STIX]{x1D6EC}$
-module (resp.
![]() $n$
-canonical left
$n$
-canonical left
![]() $\unicode[STIX]{x1D6EC}$
-module, weakly
$\unicode[STIX]{x1D6EC}$
-module, weakly
![]() $n$
-canonical
$n$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule,
$\unicode[STIX]{x1D6EC}$
-bimodule,
![]() $n$
-canonical
$n$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule) over
$\unicode[STIX]{x1D6EC}$
-bimodule) over
![]() $R$
if
$R$
if
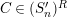 $C\in (S_{n}^{\prime })^{R}$
, and for each
$C\in (S_{n}^{\prime })^{R}$
, and for each
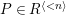 $P\in R^{\langle {<}n\rangle }$
, we have that
$P\in R^{\langle {<}n\rangle }$
, we have that
![]() $C_{P}$
is an
$C_{P}$
is an
![]() $R_{P}$
-semicanonical right
$R_{P}$
-semicanonical right
![]() $\unicode[STIX]{x1D6EC}_{P}$
-module (resp.
$\unicode[STIX]{x1D6EC}_{P}$
-module (resp.
![]() $R_{P}$
-semicanonical left
$R_{P}$
-semicanonical left
![]() $\unicode[STIX]{x1D6EC}_{P}$
-module, weakly
$\unicode[STIX]{x1D6EC}_{P}$
-module, weakly
![]() $R_{P}$
-semicanonical
$R_{P}$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}_{P}$
-bimodule,
$\unicode[STIX]{x1D6EC}_{P}$
-bimodule,
![]() $R_{P}$
-semicanonical
$R_{P}$
-semicanonical
![]() $\unicode[STIX]{x1D6EC}_{P}$
-bimodule). If we do not mention what
$\unicode[STIX]{x1D6EC}_{P}$
-bimodule). If we do not mention what
![]() $R$
is, it may mean
$R$
is, it may mean
![]() $R$
is the center of
$R$
is the center of
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Example 6.3.
- (0)
-
The zero module
 $0$
is an
$0$
is an
 $R$
-semicanonical
$R$
-semicanonical
 $\unicode[STIX]{x1D6EC}$
-bimodule.
$\unicode[STIX]{x1D6EC}$
-bimodule. - (1)
-
If
 $R$
has a dualizing complex
$R$
has a dualizing complex
 $\mathbb{I}$
, then the lowest nonvanishing cohomology group
$\mathbb{I}$
, then the lowest nonvanishing cohomology group
 $K:= Ext_{R}^{-s}(\unicode[STIX]{x1D6EC},\mathbb{I})$
is an
$K:= Ext_{R}^{-s}(\unicode[STIX]{x1D6EC},\mathbb{I})$
is an
 $R$
-semicanonical
$R$
-semicanonical
 $\unicode[STIX]{x1D6EC}$
-bimodule.
$\unicode[STIX]{x1D6EC}$
-bimodule. - (2)
-
By Lemma 5.10, any left or right
 $R$
-semicanonical module
$R$
-semicanonical module
 $K$
of
$K$
of
 $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
 $(S_{2}^{\unicode[STIX]{x1D6EC}})^{R}$
-condition. Thus a (right) semicanonical module is
$(S_{2}^{\unicode[STIX]{x1D6EC}})^{R}$
-condition. Thus a (right) semicanonical module is
 $2$
-canonical over
$2$
-canonical over
 $R/ann_{R}\unicode[STIX]{x1D6EC}$
.
$R/ann_{R}\unicode[STIX]{x1D6EC}$
. - (3)
-
If
 $K$
is (right) semicanonical (resp.
$K$
is (right) semicanonical (resp.
 $n$
-canonical) and
$n$
-canonical) and
 $L$
is a projective
$L$
is a projective
 $R$
-module such that
$R$
-module such that
 $L_{P}$
is rank at most one, then
$L_{P}$
is rank at most one, then
 $K\otimes _{R}L$
is again (right) semicanonical (resp.
$K\otimes _{R}L$
is again (right) semicanonical (resp.
 $n$
-canonical).
$n$
-canonical). - (4)
-
If
 $R$
is a normal domain and
$R$
is a normal domain and
 $C$
its rank-one reflexive module of
$C$
its rank-one reflexive module of
 $R$
, then
$R$
, then
 $C$
is a
$C$
is a
 $2$
-canonical
$2$
-canonical
 $R$
-module (here
$R$
-module (here
 $\unicode[STIX]{x1D6EC}=R$
).
$\unicode[STIX]{x1D6EC}=R$
). - (5)
-
The
 $R$
-module
$R$
-module
 $R$
is
$R$
is
 $n$
-canonical if and only if for any prime ideal
$n$
-canonical if and only if for any prime ideal
 $P$
of
$P$
of
 $R$
with
$R$
with
 $depthR_{P}<n$
,
$depthR_{P}<n$
,
 $R_{P}$
is Gorenstein. This is equivalent to say that
$R_{P}$
is Gorenstein. This is equivalent to say that
 $R$
satisfies
$R$
satisfies
 $(T_{n-1})+(S_{n})$
.
$(T_{n-1})+(S_{n})$
.
6.4
As in section 4, let
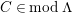 $C\in mod\unicode[STIX]{x1D6EC}$
, and set
$C\in mod\unicode[STIX]{x1D6EC}$
, and set
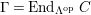 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
,
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
,
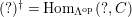 $(?)^{\dagger }= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C)$
, and
$(?)^{\dagger }= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C)$
, and
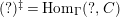 $(?)^{\ddagger }= Hom_{\unicode[STIX]{x1D6E4}}(?,C)$
. Moreover, we set
$(?)^{\ddagger }= Hom_{\unicode[STIX]{x1D6E4}}(?,C)$
. Moreover, we set
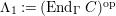 $\unicode[STIX]{x1D6EC}_{1}:=(End_{\unicode[STIX]{x1D6E4}}C)^{op}$
. The
$\unicode[STIX]{x1D6EC}_{1}:=(End_{\unicode[STIX]{x1D6E4}}C)^{op}$
. The
![]() $R$
-algebra map
$R$
-algebra map
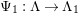 $\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is induced by the right action of
$\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is induced by the right action of
![]() $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
![]() $C$
.
$C$
.
Lemma 6.5. Let
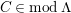 $C\in mod\unicode[STIX]{x1D6EC}$
be a
$C\in mod\unicode[STIX]{x1D6EC}$
be a
![]() $1$
-canonical
$1$
-canonical
![]() $\unicode[STIX]{x1D6EC}^{op}$
-module over
$\unicode[STIX]{x1D6EC}^{op}$
-module over
![]() $R$
. Let
$R$
. Let
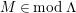 $M\in mod\unicode[STIX]{x1D6EC}$
. Then the following are equivalent.
$M\in mod\unicode[STIX]{x1D6EC}$
. Then the following are equivalent.
-
(1)
 $M\in TF(1,C)$
.
$M\in TF(1,C)$
. -
(2)
 $M\in UP(1,C)$
.
$M\in UP(1,C)$
. -
(3)
 $M\in Syz(1,C)$
.
$M\in Syz(1,C)$
. -
(4)
 $M\in (S_{1}^{\prime })_{C}^{R}$
.
$M\in (S_{1}^{\prime })_{C}^{R}$
.
Proof. (1)
![]() $\Leftrightarrow$
(2) is Lemma 4.7. (2)
$\Leftrightarrow$
(2) is Lemma 4.7. (2)
![]() $\Rightarrow$
(3) is trivial. (3)
$\Rightarrow$
(3) is trivial. (3)
![]() $\Rightarrow$
(4) follows from Lemma 4.10 immediately.
$\Rightarrow$
(4) follows from Lemma 4.10 immediately.
We prove (4)
![]() $\Rightarrow$
(1). We want to prove that
$\Rightarrow$
(1). We want to prove that
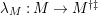 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is injective. By Example 2.11, localizing at each
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is injective. By Example 2.11, localizing at each
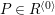 $P\in R^{\langle 0\rangle }$
, we may assume that
$P\in R^{\langle 0\rangle }$
, we may assume that
![]() $(R,\mathfrak{m})$
is zero-dimensional local. We may assume that
$(R,\mathfrak{m})$
is zero-dimensional local. We may assume that
![]() $M$
is nonzero. By assumption,
$M$
is nonzero. By assumption,
![]() $C$
is nonzero, and hence
$C$
is nonzero, and hence
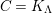 $C=K_{\unicode[STIX]{x1D6EC}}$
by assumption. As
$C=K_{\unicode[STIX]{x1D6EC}}$
by assumption. As
![]() $R$
is zero-dimensional,
$R$
is zero-dimensional,
![]() $\unicode[STIX]{x1D6EC}$
is GCM, and hence
$\unicode[STIX]{x1D6EC}$
is GCM, and hence
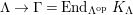 $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is an isomorphism by (5.18). As
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is an isomorphism by (5.18). As
![]() $\unicode[STIX]{x1D6EC}$
is GCM and
$\unicode[STIX]{x1D6EC}$
is GCM and
![]() $M$
is GMCM, (7) is an isomorphism. As
$M$
is GMCM, (7) is an isomorphism. As
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6E4}$
, the result follows.◻
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6E4}$
, the result follows.◻
Lemma 6.6. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical right
$1$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
, and
$R$
, and
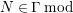 $N\in \unicode[STIX]{x1D6E4}{\rm mod}$
. Then
$N\in \unicode[STIX]{x1D6E4}{\rm mod}$
. Then
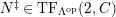 $N^{\ddagger }\in TF_{\unicode[STIX]{x1D6EC}^{op}}(2,C)$
. Similarly, for
$N^{\ddagger }\in TF_{\unicode[STIX]{x1D6EC}^{op}}(2,C)$
. Similarly, for
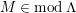 $M\in mod\unicode[STIX]{x1D6EC}$
, we have that
$M\in mod\unicode[STIX]{x1D6EC}$
, we have that
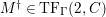 $M^{\dagger }\in TF_{\unicode[STIX]{x1D6E4}}(2,C)$
.
$M^{\dagger }\in TF_{\unicode[STIX]{x1D6E4}}(2,C)$
.
Proof. Note that
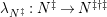 $\unicode[STIX]{x1D706}_{N^{\ddagger }}:N^{\ddagger }\rightarrow N^{\ddagger \dagger \ddagger }$
is a split monomorphism. Indeed,
$\unicode[STIX]{x1D706}_{N^{\ddagger }}:N^{\ddagger }\rightarrow N^{\ddagger \dagger \ddagger }$
is a split monomorphism. Indeed,
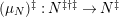 $(\unicode[STIX]{x1D707}_{N})^{\ddagger }:N^{\ddagger \dagger \ddagger }\rightarrow N^{\ddagger }$
is the left inverse. Assume that
$(\unicode[STIX]{x1D707}_{N})^{\ddagger }:N^{\ddagger \dagger \ddagger }\rightarrow N^{\ddagger }$
is the left inverse. Assume that
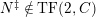 $N^{\ddagger }\notin TF(2,C)$
, then
$N^{\ddagger }\notin TF(2,C)$
, then
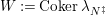 $W:= Coker\unicode[STIX]{x1D706}_{N^{\ddagger }}$
is nonzero. Let
$W:= Coker\unicode[STIX]{x1D706}_{N^{\ddagger }}$
is nonzero. Let
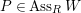 $P\in Ass_{R}W$
. As
$P\in Ass_{R}W$
. As
![]() $W$
is a submodule of
$W$
is a submodule of
![]() $N^{\ddagger \dagger \ddagger }$
,
$N^{\ddagger \dagger \ddagger }$
,
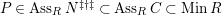 $P\in Ass_{R}N^{\ddagger \dagger \ddagger }\subset Ass_{R}C\subset MinR$
. So
$P\in Ass_{R}N^{\ddagger \dagger \ddagger }\subset Ass_{R}C\subset MinR$
. So
![]() $C_{P}$
is the right canonical module
$C_{P}$
is the right canonical module
![]() $K_{\unicode[STIX]{x1D6EC}_{P}}$
. So
$K_{\unicode[STIX]{x1D6EC}_{P}}$
. So
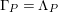 $\unicode[STIX]{x1D6E4}_{P}=\unicode[STIX]{x1D6EC}_{P}$
, and
$\unicode[STIX]{x1D6E4}_{P}=\unicode[STIX]{x1D6EC}_{P}$
, and
![]() $(\unicode[STIX]{x1D706}_{N^{\ddagger }})_{P}$
is an isomorphism. This shows that
$(\unicode[STIX]{x1D706}_{N^{\ddagger }})_{P}$
is an isomorphism. This shows that
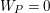 $W_{P}=0$
, and this is a contradiction. The second assertion is proved similarly.◻
$W_{P}=0$
, and this is a contradiction. The second assertion is proved similarly.◻
Lemma 6.7. Let
![]() $(R,\mathfrak{m})$
be local, and assume that
$(R,\mathfrak{m})$
be local, and assume that
![]() $K_{\unicode[STIX]{x1D6EC}}$
exists. Let
$K_{\unicode[STIX]{x1D6EC}}$
exists. Let
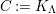 $C:=K_{\unicode[STIX]{x1D6EC}}$
. If
$C:=K_{\unicode[STIX]{x1D6EC}}$
. If
![]() $\unicode[STIX]{x1D6EC}$
is GCM,
$\unicode[STIX]{x1D6EC}$
is GCM,
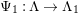 $\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is an isomorphism.
$\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is an isomorphism.
Proof. As
![]() $C$
possesses a bimodule structure, we have a canonical map
$C$
possesses a bimodule structure, we have a canonical map
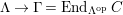 $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
, which is an isomorphism as
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
, which is an isomorphism as
![]() $\unicode[STIX]{x1D6EC}$
is GCM by (5.18). So
$\unicode[STIX]{x1D6EC}$
is GCM by (5.18). So
![]() $\unicode[STIX]{x1D6EC}_{1}$
is identified with
$\unicode[STIX]{x1D6EC}_{1}$
is identified with
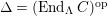 $\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then
$\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then
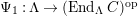 $\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow (End_{\unicode[STIX]{x1D6EC}}C)^{op}$
is an isomorphism again by (5.18).◻
$\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow (End_{\unicode[STIX]{x1D6EC}}C)^{op}$
is an isomorphism again by (5.18).◻
Lemma 6.8. If
![]() $C$
satisfies the
$C$
satisfies the
![]() $(S_{1}^{\prime })^{R}$
condition, then
$(S_{1}^{\prime })^{R}$
condition, then
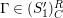 $\unicode[STIX]{x1D6E4}\in (S_{1}^{\prime })_{C}^{R}$
and
$\unicode[STIX]{x1D6E4}\in (S_{1}^{\prime })_{C}^{R}$
and
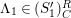 $\unicode[STIX]{x1D6EC}_{1}\in (S_{1}^{\prime })_{C}^{R}$
. Moreover,
$\unicode[STIX]{x1D6EC}_{1}\in (S_{1}^{\prime })_{C}^{R}$
. Moreover,
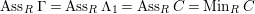 $Ass_{R}\unicode[STIX]{x1D6E4}= Ass_{R}\unicode[STIX]{x1D6EC}_{1}= Ass_{R}C= Min_{R}C$
.
$Ass_{R}\unicode[STIX]{x1D6E4}= Ass_{R}\unicode[STIX]{x1D6EC}_{1}= Ass_{R}C= Min_{R}C$
.
Proof. The first assertion is by
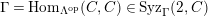 $\unicode[STIX]{x1D6E4}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(C,C)\in Syz_{\unicode[STIX]{x1D6E4}}(2,C)$
, and
$\unicode[STIX]{x1D6E4}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(C,C)\in Syz_{\unicode[STIX]{x1D6E4}}(2,C)$
, and
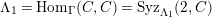 $\unicode[STIX]{x1D6EC}_{1}= Hom_{\unicode[STIX]{x1D6E4}}(C,C)= Syz_{\unicode[STIX]{x1D6EC}_{1}}(2,C)$
. We prove the second assertion.
$\unicode[STIX]{x1D6EC}_{1}= Hom_{\unicode[STIX]{x1D6E4}}(C,C)= Syz_{\unicode[STIX]{x1D6EC}_{1}}(2,C)$
. We prove the second assertion.
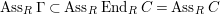 $Ass_{R}\unicode[STIX]{x1D6E4}\subset Ass_{R} End_{R}C= Ass_{R}C$
.
$Ass_{R}\unicode[STIX]{x1D6E4}\subset Ass_{R} End_{R}C= Ass_{R}C$
.
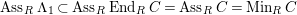 $Ass_{R}\unicode[STIX]{x1D6EC}_{1}\subset Ass_{R} End_{R}C= Ass_{R}C= Min_{R}C$
. It remains to show that
$Ass_{R}\unicode[STIX]{x1D6EC}_{1}\subset Ass_{R} End_{R}C= Ass_{R}C= Min_{R}C$
. It remains to show that
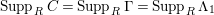 $Supp_{R}C= Supp_{R}\unicode[STIX]{x1D6E4}= Supp_{R}\unicode[STIX]{x1D6EC}_{1}$
. Let
$Supp_{R}C= Supp_{R}\unicode[STIX]{x1D6E4}= Supp_{R}\unicode[STIX]{x1D6EC}_{1}$
. Let
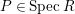 $P\in SpecR$
. If
$P\in SpecR$
. If
![]() $C_{P}=0$
, then
$C_{P}=0$
, then
![]() $\unicode[STIX]{x1D6E4}_{P}=0$
and
$\unicode[STIX]{x1D6E4}_{P}=0$
and
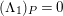 $(\unicode[STIX]{x1D6EC}_{1})_{P}=0$
. On the other hand, if
$(\unicode[STIX]{x1D6EC}_{1})_{P}=0$
. On the other hand, if
![]() $C_{P}\neq 0$
, then the identity map
$C_{P}\neq 0$
, then the identity map
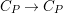 $C_{P}\rightarrow C_{P}$
is not zero, and hence
$C_{P}\rightarrow C_{P}$
is not zero, and hence
![]() $\unicode[STIX]{x1D6E4}_{P}\neq 0$
and
$\unicode[STIX]{x1D6E4}_{P}\neq 0$
and
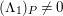 $(\unicode[STIX]{x1D6EC}_{1})_{P}\neq 0$
.◻
$(\unicode[STIX]{x1D6EC}_{1})_{P}\neq 0$
.◻
6.9
Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical right
$1$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. Define
$R$
. Define
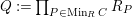 $Q:=\prod _{P\in Min_{R}C}R_{P}$
. If
$Q:=\prod _{P\in Min_{R}C}R_{P}$
. If
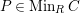 $P\in Min_{R}C$
, then
$P\in Min_{R}C$
, then
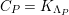 $C_{P}=K_{\unicode[STIX]{x1D6EC}_{P}}$
. Hence
$C_{P}=K_{\unicode[STIX]{x1D6EC}_{P}}$
. Hence
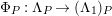 $\unicode[STIX]{x1D6F7}_{P}:\unicode[STIX]{x1D6EC}_{P}\rightarrow (\unicode[STIX]{x1D6EC}_{1})_{P}$
is an isomorphism by Lemma 6.7. So
$\unicode[STIX]{x1D6F7}_{P}:\unicode[STIX]{x1D6EC}_{P}\rightarrow (\unicode[STIX]{x1D6EC}_{1})_{P}$
is an isomorphism by Lemma 6.7. So
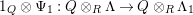 $1_{Q}\otimes \unicode[STIX]{x1D6F9}_{1}:Q\otimes _{R}\unicode[STIX]{x1D6EC}\rightarrow Q\otimes _{R}\unicode[STIX]{x1D6EC}_{1}$
is also an isomorphism. As
$1_{Q}\otimes \unicode[STIX]{x1D6F9}_{1}:Q\otimes _{R}\unicode[STIX]{x1D6EC}\rightarrow Q\otimes _{R}\unicode[STIX]{x1D6EC}_{1}$
is also an isomorphism. As
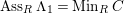 $Ass_{R}\unicode[STIX]{x1D6EC}_{1}= Min_{R}C$
, we have that
$Ass_{R}\unicode[STIX]{x1D6EC}_{1}= Min_{R}C$
, we have that
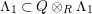 $\unicode[STIX]{x1D6EC}_{1}\subset Q\otimes _{R}\unicode[STIX]{x1D6EC}_{1}$
.
$\unicode[STIX]{x1D6EC}_{1}\subset Q\otimes _{R}\unicode[STIX]{x1D6EC}_{1}$
.
Lemma 6.10. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical right
$1$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. If
$R$
. If
![]() $\unicode[STIX]{x1D6EC}$
is commutative, then so are
$\unicode[STIX]{x1D6EC}$
is commutative, then so are
![]() $\unicode[STIX]{x1D6EC}_{1}$
and
$\unicode[STIX]{x1D6EC}_{1}$
and
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Proof. As
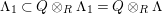 $\unicode[STIX]{x1D6EC}_{1}\subset Q\otimes _{R}\unicode[STIX]{x1D6EC}_{1}=Q\otimes _{R}\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D6EC}_{1}\subset Q\otimes _{R}\unicode[STIX]{x1D6EC}_{1}=Q\otimes _{R}\unicode[STIX]{x1D6EC}$
and
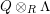 $Q\otimes _{R}\unicode[STIX]{x1D6EC}$
is commutative,
$Q\otimes _{R}\unicode[STIX]{x1D6EC}$
is commutative,
![]() $\unicode[STIX]{x1D6EC}_{1}$
is a commutative ring. We prove that
$\unicode[STIX]{x1D6EC}_{1}$
is a commutative ring. We prove that
![]() $\unicode[STIX]{x1D6E4}$
is commutative. As
$\unicode[STIX]{x1D6E4}$
is commutative. As
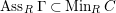 $Ass_{R}\unicode[STIX]{x1D6E4}\subset Min_{R}C$
,
$Ass_{R}\unicode[STIX]{x1D6E4}\subset Min_{R}C$
,
![]() $\unicode[STIX]{x1D6E4}$
is a subring of
$\unicode[STIX]{x1D6E4}$
is a subring of
![]() $Q\otimes \unicode[STIX]{x1D6E4}$
. As
$Q\otimes \unicode[STIX]{x1D6E4}$
. As
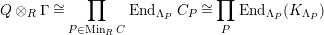 $$\begin{eqnarray}Q\otimes _{R}\unicode[STIX]{x1D6E4}\cong \mathop{\prod }_{P\in Min_{R}C} End_{\unicode[STIX]{x1D6EC}_{P}}C_{P}\cong \mathop{\prod }_{P} End_{\unicode[STIX]{x1D6EC}_{P}}(K_{\unicode[STIX]{x1D6EC}_{P}})\end{eqnarray}$$
$$\begin{eqnarray}Q\otimes _{R}\unicode[STIX]{x1D6E4}\cong \mathop{\prod }_{P\in Min_{R}C} End_{\unicode[STIX]{x1D6EC}_{P}}C_{P}\cong \mathop{\prod }_{P} End_{\unicode[STIX]{x1D6EC}_{P}}(K_{\unicode[STIX]{x1D6EC}_{P}})\end{eqnarray}$$
and
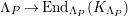 $\unicode[STIX]{x1D6EC}_{P}\rightarrow End_{\unicode[STIX]{x1D6EC}_{P}}(K_{\unicode[STIX]{x1D6EC}_{P}})$
is an isomorphism (as
$\unicode[STIX]{x1D6EC}_{P}\rightarrow End_{\unicode[STIX]{x1D6EC}_{P}}(K_{\unicode[STIX]{x1D6EC}_{P}})$
is an isomorphism (as
![]() $\unicode[STIX]{x1D6EC}_{P}$
is zero-dimensional),
$\unicode[STIX]{x1D6EC}_{P}$
is zero-dimensional),
![]() $Q\otimes _{R}\unicode[STIX]{x1D6E4}$
is, and hence
$Q\otimes _{R}\unicode[STIX]{x1D6E4}$
is, and hence
![]() $\unicode[STIX]{x1D6E4}$
is also, commutative.◻
$\unicode[STIX]{x1D6E4}$
is also, commutative.◻
Lemma 6.11. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical right
$1$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. Let
$R$
. Let
![]() $M$
and
$M$
and
![]() $N$
be left (resp. right, bi-) modules of
$N$
be left (resp. right, bi-) modules of
![]() $\unicode[STIX]{x1D6EC}_{1}$
, and assume that
$\unicode[STIX]{x1D6EC}_{1}$
, and assume that
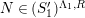 $N\in (S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1},R}$
. Let
$N\in (S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1},R}$
. Let
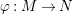 $\unicode[STIX]{x1D711}:M\rightarrow N$
be a
$\unicode[STIX]{x1D711}:M\rightarrow N$
be a
![]() $\unicode[STIX]{x1D6EC}$
-homomorphism of left (resp. right, bi-) modules. Then
$\unicode[STIX]{x1D6EC}$
-homomorphism of left (resp. right, bi-) modules. Then
![]() $\unicode[STIX]{x1D711}$
is a
$\unicode[STIX]{x1D711}$
is a
![]() $\unicode[STIX]{x1D6EC}_{1}$
-homomorphism of left (resp. right, bi-) modules.
$\unicode[STIX]{x1D6EC}_{1}$
-homomorphism of left (resp. right, bi-) modules.
Proof. Let
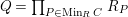 $Q=\prod _{P\in Min_{R}C}R_{P}$
. Then we have a commutative diagram
$Q=\prod _{P\in Min_{R}C}R_{P}$
. Then we have a commutative diagram
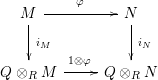
where
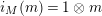 $i_{M}(m)=1\otimes m$
and
$i_{M}(m)=1\otimes m$
and
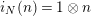 $i_{N}(n)=1\otimes n$
. Clearly,
$i_{N}(n)=1\otimes n$
. Clearly,
![]() $i_{M}$
and
$i_{M}$
and
![]() $i_{N}$
are
$i_{N}$
are
![]() $\unicode[STIX]{x1D6EC}_{1}$
-linear. As
$\unicode[STIX]{x1D6EC}_{1}$
-linear. As
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() $\unicode[STIX]{x1D6EC}$
-linear,
$\unicode[STIX]{x1D6EC}$
-linear,
![]() $1\otimes \unicode[STIX]{x1D711}$
is
$1\otimes \unicode[STIX]{x1D711}$
is
![]() $Q\otimes \unicode[STIX]{x1D6EC}$
-linear. Since
$Q\otimes \unicode[STIX]{x1D6EC}$
-linear. Since
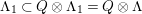 $\unicode[STIX]{x1D6EC}_{1}\subset Q\otimes \unicode[STIX]{x1D6EC}_{1}=Q\otimes \unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D6EC}_{1}\subset Q\otimes \unicode[STIX]{x1D6EC}_{1}=Q\otimes \unicode[STIX]{x1D6EC}$
,
![]() $1\otimes \unicode[STIX]{x1D711}$
is
$1\otimes \unicode[STIX]{x1D711}$
is
![]() $\unicode[STIX]{x1D6EC}_{1}$
-linear. As
$\unicode[STIX]{x1D6EC}_{1}$
-linear. As
![]() $i_{N}$
is injective, it is easy to see that
$i_{N}$
is injective, it is easy to see that
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() $\unicode[STIX]{x1D6EC}_{1}$
-linear.◻
$\unicode[STIX]{x1D6EC}_{1}$
-linear.◻
Lemma 6.12. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical right
$1$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. Then the restriction
$R$
. Then the restriction
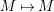 $M\mapsto M$
is a full and faithful functor from
$M\mapsto M$
is a full and faithful functor from
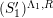 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1},R}$
to
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1},R}$
to
![]() $(S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC},R}$
. Similarly, it gives a full and faithful functors
$(S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC},R}$
. Similarly, it gives a full and faithful functors
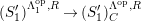 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
and
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
and
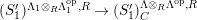 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}\otimes _{R}\unicode[STIX]{x1D6EC}_{1}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
.
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}\otimes _{R}\unicode[STIX]{x1D6EC}_{1}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
.
Proof. We only consider the case of left modules. If
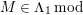 $M\in \unicode[STIX]{x1D6EC}_{1} mod$
, then it is a homomorphic image of
$M\in \unicode[STIX]{x1D6EC}_{1} mod$
, then it is a homomorphic image of
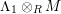 $\unicode[STIX]{x1D6EC}_{1}\otimes _{R}M$
. Hence
$\unicode[STIX]{x1D6EC}_{1}\otimes _{R}M$
. Hence
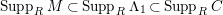 $Supp_{R}M\subset Supp_{R}\unicode[STIX]{x1D6EC}_{1}\subset Supp_{R}C$
. So the functor is well defined and obviously faithful. By Lemma 6.11, it is also full, and we are done.◻
$Supp_{R}M\subset Supp_{R}\unicode[STIX]{x1D6EC}_{1}\subset Supp_{R}C$
. So the functor is well defined and obviously faithful. By Lemma 6.11, it is also full, and we are done.◻
6.13
Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical
$1$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
. Then the left action of
$R$
. Then the left action of
![]() $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
![]() $C$
induces an
$C$
induces an
![]() $R$
-algebra map
$R$
-algebra map
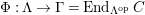 $\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Let
$\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Let
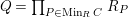 $Q=\prod _{P\in Min_{R}C}R_{P}$
. Then
$Q=\prod _{P\in Min_{R}C}R_{P}$
. Then
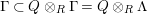 $\unicode[STIX]{x1D6E4}\subset Q\otimes _{R}\unicode[STIX]{x1D6E4}=Q\otimes _{R}\unicode[STIX]{x1D6EC}$
. From this we get
$\unicode[STIX]{x1D6E4}\subset Q\otimes _{R}\unicode[STIX]{x1D6E4}=Q\otimes _{R}\unicode[STIX]{x1D6EC}$
. From this we get
Lemma 6.14. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical
$1$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
. Let
$R$
. Let
![]() $M$
and
$M$
and
![]() $N$
be left (resp. right, bi-) modules of
$N$
be left (resp. right, bi-) modules of
![]() $\unicode[STIX]{x1D6E4}$
, and assume that
$\unicode[STIX]{x1D6E4}$
, and assume that
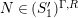 $N\in (S_{1}^{\prime })^{\unicode[STIX]{x1D6E4},R}$
. Let
$N\in (S_{1}^{\prime })^{\unicode[STIX]{x1D6E4},R}$
. Let
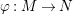 $\unicode[STIX]{x1D711}:M\rightarrow N$
be a
$\unicode[STIX]{x1D711}:M\rightarrow N$
be a
![]() $\unicode[STIX]{x1D6EC}$
-homomorphism of left (resp. right, bi-) modules. Then
$\unicode[STIX]{x1D6EC}$
-homomorphism of left (resp. right, bi-) modules. Then
![]() $\unicode[STIX]{x1D711}$
is a
$\unicode[STIX]{x1D711}$
is a
![]() $\unicode[STIX]{x1D6E4}$
-homomorphism of left (resp. right, bi-) modules.
$\unicode[STIX]{x1D6E4}$
-homomorphism of left (resp. right, bi-) modules.
Proof. Similar to Lemma 6.11, and left to the reader. ◻
Corollary 6.15. Let
![]() $C$
be as above.
$C$
be as above.
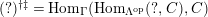 $(?)^{\dagger \ddagger }= Hom_{\unicode[STIX]{x1D6E4}}(Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C),C)$
is canonically isomorphic to
$(?)^{\dagger \ddagger }= Hom_{\unicode[STIX]{x1D6E4}}(Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C),C)$
is canonically isomorphic to
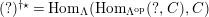 $(?)^{\dagger \star }= Hom_{\unicode[STIX]{x1D6EC}}(Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C),C)$
, where
$(?)^{\dagger \star }= Hom_{\unicode[STIX]{x1D6EC}}(Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C),C)$
, where
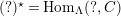 $(?)^{\star }= Hom_{\unicode[STIX]{x1D6EC}}(?,C)$
.
$(?)^{\star }= Hom_{\unicode[STIX]{x1D6EC}}(?,C)$
.
Proof. This is immediate by Lemma 6.14. ◻
Lemma 6.16. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical
$1$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
. Then
$R$
. Then
![]() $\unicode[STIX]{x1D6F7}$
induces a full and faithful functor
$\unicode[STIX]{x1D6F7}$
induces a full and faithful functor
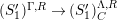 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6E4},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC},R}$
. Similarly,
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6E4},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC},R}$
. Similarly,
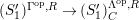 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6E4}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
and
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6E4}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
and
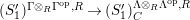 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E4}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
are also induced.
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E4}^{op},R}\rightarrow (S_{1}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
are also induced.
Proof. Similar to Lemma 6.12, and left to the reader. ◻
Corollary 6.17. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical
$1$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule. Set
$\unicode[STIX]{x1D6EC}$
-bimodule. Set
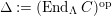 $\unicode[STIX]{x1D6E5}:=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then the canonical map
$\unicode[STIX]{x1D6E5}:=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then the canonical map
![]() $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}$
induces an equality
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}$
induces an equality
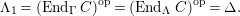 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{1}=(End_{\unicode[STIX]{x1D6E4}}C)^{op}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}=\unicode[STIX]{x1D6E5}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{1}=(End_{\unicode[STIX]{x1D6E4}}C)^{op}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}=\unicode[STIX]{x1D6E5}.\end{eqnarray}$$
Similarly, we have
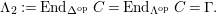 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{2}:= End_{\unicode[STIX]{x1D6E5}^{op}}C= End_{\unicode[STIX]{x1D6EC}^{op}}C=\unicode[STIX]{x1D6E4}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{2}:= End_{\unicode[STIX]{x1D6E5}^{op}}C= End_{\unicode[STIX]{x1D6EC}^{op}}C=\unicode[STIX]{x1D6E4}.\end{eqnarray}$$
Proof. As
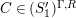 $C\in (S_{1}^{\prime })^{\unicode[STIX]{x1D6E4},R}$
, the first assertion follows from Lemma 6.16. The second assertion is proved by left–right symmetry.◻
$C\in (S_{1}^{\prime })^{\unicode[STIX]{x1D6E4},R}$
, the first assertion follows from Lemma 6.16. The second assertion is proved by left–right symmetry.◻
Lemma 6.18. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical right
$1$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. Set
$R$
. Set
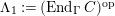 $\unicode[STIX]{x1D6EC}_{1}:=(End_{\unicode[STIX]{x1D6E4}}C)^{op}$
. Let
$\unicode[STIX]{x1D6EC}_{1}:=(End_{\unicode[STIX]{x1D6E4}}C)^{op}$
. Let
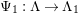 $\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
be the canonical map induced by the right action of
$\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
be the canonical map induced by the right action of
![]() $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
![]() $C$
. Then
$C$
. Then
![]() $\unicode[STIX]{x1D6F9}_{1}$
is injective if and only if
$\unicode[STIX]{x1D6F9}_{1}$
is injective if and only if
![]() $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
![]() $(S_{1}^{\prime })^{R}$
condition and
$(S_{1}^{\prime })^{R}$
condition and
![]() $C$
is
$C$
is
![]() $\unicode[STIX]{x1D6EC}$
-full over
$\unicode[STIX]{x1D6EC}$
-full over
![]() $R$
.
$R$
.
Proof.
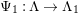 $\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is nothing but
$\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is nothing but
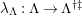 $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6EC}}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}^{\dagger \ddagger }$
, and the result follows from Lemma 6.5 immediately.◻
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6EC}}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}^{\dagger \ddagger }$
, and the result follows from Lemma 6.5 immediately.◻
Lemma 6.19. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical
$1$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
. Then the following are equivalent.
$R$
. Then the following are equivalent.
-
(1) The canonical map
 $\unicode[STIX]{x1D6F9}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E5}$
is injective, where
$\unicode[STIX]{x1D6F9}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E5}$
is injective, where
 $\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
, and the map is induced by the right action of
$\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
, and the map is induced by the right action of
 $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
 $C$
.
$C$
. -
(2)
 $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
 $(S_{1}^{\prime })^{R}$
condition, and
$(S_{1}^{\prime })^{R}$
condition, and
 $C$
is
$C$
is
 $\unicode[STIX]{x1D6EC}$
-full over
$\unicode[STIX]{x1D6EC}$
-full over
 $R$
.
$R$
. -
(3) The canonical map
 $\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}$
is injective, where the map is induced by the left action of
$\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}$
is injective, where the map is induced by the left action of
 $\unicode[STIX]{x1D6EC}$
on
$\unicode[STIX]{x1D6EC}$
on
 $C$
.
$C$
.
Proof. By Corollary 6.17, we have that
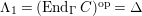 $\unicode[STIX]{x1D6EC}_{1}=(End_{\unicode[STIX]{x1D6E4}}C)^{op}=\unicode[STIX]{x1D6E5}$
. So (1)
$\unicode[STIX]{x1D6EC}_{1}=(End_{\unicode[STIX]{x1D6E4}}C)^{op}=\unicode[STIX]{x1D6E5}$
. So (1)
![]() $\Leftrightarrow$
(2) is a consequence of Lemma 6.18.
$\Leftrightarrow$
(2) is a consequence of Lemma 6.18.
Reversing the roles of the left and the right, we get (2)
![]() $\Leftrightarrow$
(3) immediately.◻
$\Leftrightarrow$
(3) immediately.◻
Lemma 6.20. Let
![]() $C$
be a
$C$
be a
![]() $1$
-canonical right
$1$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. Then the canonical map
$R$
. Then the canonical map
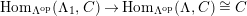 $$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC}_{1},C)\rightarrow Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},C)\cong C\end{eqnarray}$$
$$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC}_{1},C)\rightarrow Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},C)\cong C\end{eqnarray}$$
induced by the canonical map
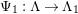 $\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is an isomorphism of
$\unicode[STIX]{x1D6F9}_{1}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is an isomorphism of
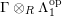 $\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6EC}_{1}^{op}$
-modules.
$\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6EC}_{1}^{op}$
-modules.
Proof. The composite map
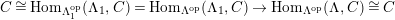 $$\begin{eqnarray}C\cong Hom_{\unicode[STIX]{x1D6EC}_{1}^{op}}(\unicode[STIX]{x1D6EC}_{1},C)= Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC}_{1},C)\rightarrow Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},C)\cong C\end{eqnarray}$$
$$\begin{eqnarray}C\cong Hom_{\unicode[STIX]{x1D6EC}_{1}^{op}}(\unicode[STIX]{x1D6EC}_{1},C)= Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC}_{1},C)\rightarrow Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},C)\cong C\end{eqnarray}$$
is the identity. The map is a
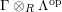 $\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}$
-homomorphism. It is also
$\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}$
-homomorphism. It is also
![]() $\unicode[STIX]{x1D6EC}_{1}^{op}$
-linear by Lemma 6.12.◻
$\unicode[STIX]{x1D6EC}_{1}^{op}$
-linear by Lemma 6.12.◻
6.21
When
![]() $(R,\mathfrak{m})$
is local and
$(R,\mathfrak{m})$
is local and
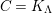 $C=K_{\unicode[STIX]{x1D6EC}}$
, then
$C=K_{\unicode[STIX]{x1D6EC}}$
, then
![]() $\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6E5}$
, and the map (8) is an isomorphism of
$\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6E5}$
, and the map (8) is an isomorphism of
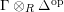 $\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E5}^{op}$
-modules from
$\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E5}^{op}$
-modules from
![]() $K_{\unicode[STIX]{x1D6E5}}$
and
$K_{\unicode[STIX]{x1D6E5}}$
and
![]() $K_{\unicode[STIX]{x1D6EC}}$
, where
$K_{\unicode[STIX]{x1D6EC}}$
, where
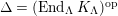 $\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}$
. Indeed, to verify this, we may assume that
$\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}$
. Indeed, to verify this, we may assume that
![]() $R$
is complete regular local with
$R$
is complete regular local with
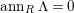 $ann_{R}\unicode[STIX]{x1D6EC}=0$
, and hence
$ann_{R}\unicode[STIX]{x1D6EC}=0$
, and hence
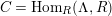 $C= Hom_{R}(\unicode[STIX]{x1D6EC},R)$
, and
$C= Hom_{R}(\unicode[STIX]{x1D6EC},R)$
, and
![]() $C$
is a
$C$
is a
![]() $2$
-canonical
$2$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
; see (6.3). So (6.17) and Lemma 6.20 apply. Hence we have
$R$
; see (6.3). So (6.17) and Lemma 6.20 apply. Hence we have
Corollary 6.22. Let
![]() $(R,\mathfrak{m})$
be a local ring with a canonical module
$(R,\mathfrak{m})$
be a local ring with a canonical module
![]() $K_{\unicode[STIX]{x1D6EC}}$
of
$K_{\unicode[STIX]{x1D6EC}}$
of
![]() $\unicode[STIX]{x1D6EC}$
. Then
$\unicode[STIX]{x1D6EC}$
. Then
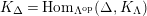 $K_{\unicode[STIX]{x1D6E5}}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6E5},K_{\unicode[STIX]{x1D6EC}})$
is isomorphic to
$K_{\unicode[STIX]{x1D6E5}}= Hom_{\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6E5},K_{\unicode[STIX]{x1D6EC}})$
is isomorphic to
![]() $K_{\unicode[STIX]{x1D6EC}}$
as a
$K_{\unicode[STIX]{x1D6EC}}$
as a
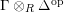 $\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E5}^{op}$
-module, where
$\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E5}^{op}$
-module, where
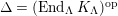 $\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}$
.◻
$\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}$
.◻
Lemma 6.23. Let
![]() $n\geqslant 1$
. If
$n\geqslant 1$
. If
![]() $C$
is an
$C$
is an
![]() $n$
-canonical right
$n$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
, then
$R$
, then
-
(1)
 $C$
is an
$C$
is an
 $n$
-canonical right
$n$
-canonical right
 $\unicode[STIX]{x1D6EC}_{1}$
-module over
$\unicode[STIX]{x1D6EC}_{1}$
-module over
 $R$
.
$R$
. -
(2)
 $C$
is an
$C$
is an
 $n$
-canonical left
$n$
-canonical left
 $\unicode[STIX]{x1D6E4}$
-module over
$\unicode[STIX]{x1D6E4}$
-module over
 $R$
.
$R$
.
Proof. (1) As the
![]() $(S_{n}^{\prime })$
-condition holds, it suffices to prove that for
$(S_{n}^{\prime })$
-condition holds, it suffices to prove that for
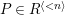 $P\in R^{\langle {<}n\rangle }$
with
$P\in R^{\langle {<}n\rangle }$
with
![]() $C_{P}\neq 0$
, we have
$C_{P}\neq 0$
, we have
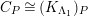 $C_{P}\cong (K_{\unicode[STIX]{x1D6EC}_{1}})_{P}$
as a right
$C_{P}\cong (K_{\unicode[STIX]{x1D6EC}_{1}})_{P}$
as a right
![]() $(\unicode[STIX]{x1D6EC}_{1})_{P}$
-module. After localization, replacing
$(\unicode[STIX]{x1D6EC}_{1})_{P}$
-module. After localization, replacing
![]() $R$
by
$R$
by
![]() $R_{P}$
, we may assume that
$R_{P}$
, we may assume that
![]() $R$
is local and
$R$
is local and
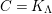 $C=K_{\unicode[STIX]{x1D6EC}}$
. Then
$C=K_{\unicode[STIX]{x1D6EC}}$
. Then
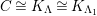 $C\cong K_{\unicode[STIX]{x1D6EC}}\cong K_{\unicode[STIX]{x1D6EC}_{1}}$
as right
$C\cong K_{\unicode[STIX]{x1D6EC}}\cong K_{\unicode[STIX]{x1D6EC}_{1}}$
as right
![]() $\unicode[STIX]{x1D6EC}$
-modules. Both
$\unicode[STIX]{x1D6EC}$
-modules. Both
![]() $C$
and
$C$
and
![]() $K_{\unicode[STIX]{x1D6EC}_{1}}$
are in
$K_{\unicode[STIX]{x1D6EC}_{1}}$
are in
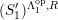 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}^{op},R}$
, and isomorphic in
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}^{op},R}$
, and isomorphic in
![]() ${\rm mod}\unicode[STIX]{x1D6EC}$
. So they are isomorphic in
${\rm mod}\unicode[STIX]{x1D6EC}$
. So they are isomorphic in
![]() ${\rm mod}\unicode[STIX]{x1D6EC}_{1}$
by Lemma 6.12.
${\rm mod}\unicode[STIX]{x1D6EC}_{1}$
by Lemma 6.12.
(2) Similarly, assuming that
![]() $R$
is local and
$R$
is local and
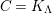 $C=K_{\unicode[STIX]{x1D6EC}}$
, it suffices to show that
$C=K_{\unicode[STIX]{x1D6EC}}$
, it suffices to show that
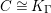 $C\cong K_{\unicode[STIX]{x1D6E4}}$
as left
$C\cong K_{\unicode[STIX]{x1D6E4}}$
as left
![]() $\unicode[STIX]{x1D6E4}$
-modules. Identifying
$\unicode[STIX]{x1D6E4}$
-modules. Identifying
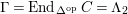 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6E5}^{op}}C=\unicode[STIX]{x1D6EC}_{2}$
and using the left–right symmetry, this is the same as the proof of (1).◻
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6E5}^{op}}C=\unicode[STIX]{x1D6EC}_{2}$
and using the left–right symmetry, this is the same as the proof of (1).◻
Lemma 6.24. Let
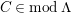 $C\in mod\unicode[STIX]{x1D6EC}$
be a
$C\in mod\unicode[STIX]{x1D6EC}$
be a
![]() $2$
-canonical right
$2$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. Let
$R$
. Let
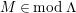 $M\in mod\unicode[STIX]{x1D6EC}$
. Then the following are equivalent.
$M\in mod\unicode[STIX]{x1D6EC}$
. Then the following are equivalent.
-
(1)
 $M\in TF(2,C)$
.
$M\in TF(2,C)$
. -
(2)
 $M\in UP(2,C)$
.
$M\in UP(2,C)$
. -
(3)
 $M\in Syz(2,C)$
.
$M\in Syz(2,C)$
. -
(4)
 $M\in (S_{2}^{\prime })_{C}^{R}$
.
$M\in (S_{2}^{\prime })_{C}^{R}$
.
Proof. We may assume that
![]() $\unicode[STIX]{x1D6EC}$
is a faithful
$\unicode[STIX]{x1D6EC}$
is a faithful
![]() $R$
-module. (1)
$R$
-module. (1)
![]() $\Leftrightarrow$
(2)
$\Leftrightarrow$
(2)
![]() $\Rightarrow$
(3)
$\Rightarrow$
(3)
![]() $\Rightarrow$
(4) is easy. We show (4)
$\Rightarrow$
(4) is easy. We show (4)
![]() $\Rightarrow$
(1). By Example 2.11, localizing at each
$\Rightarrow$
(1). By Example 2.11, localizing at each
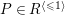 $P\in R^{\langle {\leqslant}1\rangle }$
, we may assume that
$P\in R^{\langle {\leqslant}1\rangle }$
, we may assume that
![]() $R$
is a Noetherian local ring of dimension at most one. So the formal fibers of
$R$
is a Noetherian local ring of dimension at most one. So the formal fibers of
![]() $R$
are zero-dimensional, and hence
$R$
are zero-dimensional, and hence
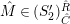 $\hat{M}\in (S_{2}^{\prime })_{{\hat{C}}}^{\hat{R}}$
, where
$\hat{M}\in (S_{2}^{\prime })_{{\hat{C}}}^{\hat{R}}$
, where
![]() $\hat{?}$
denotes the completion. So we may further assume that
$\hat{?}$
denotes the completion. So we may further assume that
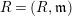 $R=(R,\mathfrak{m})$
is complete local. We may assume that
$R=(R,\mathfrak{m})$
is complete local. We may assume that
![]() $M\neq 0$
so that
$M\neq 0$
so that
![]() $C\neq 0$
and hence
$C\neq 0$
and hence
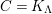 $C=K_{\unicode[STIX]{x1D6EC}}$
. The case
$C=K_{\unicode[STIX]{x1D6EC}}$
. The case
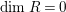 $\dim R=0$
is similar to the proof of Lemma 6.5, so we prove the case that
$\dim R=0$
is similar to the proof of Lemma 6.5, so we prove the case that
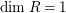 $\dim R=1$
. Note that
$\dim R=1$
. Note that
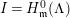 $I=H_{\mathfrak{m}}^{0}(\unicode[STIX]{x1D6EC})$
is a two-sided ideal of
$I=H_{\mathfrak{m}}^{0}(\unicode[STIX]{x1D6EC})$
is a two-sided ideal of
![]() $\unicode[STIX]{x1D6EC}$
, and any module in
$\unicode[STIX]{x1D6EC}$
, and any module in
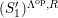 $(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}^{op},R}$
is annihilated by
$(S_{1}^{\prime })^{\unicode[STIX]{x1D6EC}^{op},R}$
is annihilated by
![]() $I$
. Replacing
$I$
. Replacing
![]() $\unicode[STIX]{x1D6EC}$
by
$\unicode[STIX]{x1D6EC}$
by
![]() $\unicode[STIX]{x1D6EC}/I$
, we may assume that
$\unicode[STIX]{x1D6EC}/I$
, we may assume that
![]() $\unicode[STIX]{x1D6EC}$
is a maximal Cohen–Macaulay
$\unicode[STIX]{x1D6EC}$
is a maximal Cohen–Macaulay
![]() $R$
-module. Then (7) is an isomorphism. As
$R$
-module. Then (7) is an isomorphism. As
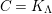 $C=K_{\unicode[STIX]{x1D6EC}}$
and
$C=K_{\unicode[STIX]{x1D6EC}}$
and
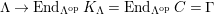 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}= End_{\unicode[STIX]{x1D6EC}^{op}}C=\unicode[STIX]{x1D6E4}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}= End_{\unicode[STIX]{x1D6EC}^{op}}C=\unicode[STIX]{x1D6E4}\end{eqnarray}$$
is an
![]() $R$
-algebra isomorphism, we have that
$R$
-algebra isomorphism, we have that
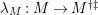 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is identified with the isomorphism (7), as desired.◻
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is identified with the isomorphism (7), as desired.◻
Corollary 6.25. Let
![]() $C$
be a
$C$
be a
![]() $2$
-canonical right
$2$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
. Then the canonical map
$R$
. Then the canonical map
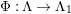 $\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is an isomorphism if and only if
$\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}_{1}$
is an isomorphism if and only if
![]() $\unicode[STIX]{x1D6EC}$
satisfies
$\unicode[STIX]{x1D6EC}$
satisfies
![]() $(S_{2}^{\prime })^{R}$
and
$(S_{2}^{\prime })^{R}$
and
![]() $C$
is full.
$C$
is full.
Proof. Follows immediately by Lemma 6.24 applied to
![]() $M=\unicode[STIX]{x1D6EC}$
.◻
$M=\unicode[STIX]{x1D6EC}$
.◻
6.26
Let
![]() $C$
be a
$C$
be a
![]() $2$
-canonical
$2$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule. Let
$\unicode[STIX]{x1D6EC}$
-bimodule. Let
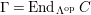 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
and
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
and
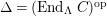 $\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then by the left multiplication, an
$\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then by the left multiplication, an
![]() $R$
-algebra map
$R$
-algebra map
![]() $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}$
is induced, while by the right multiplication, an
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E4}$
is induced, while by the right multiplication, an
![]() $R$
-algebra map
$R$
-algebra map
![]() $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E5}$
is induced. Let
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E5}$
is induced. Let
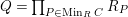 $Q=\prod _{P\in Min_{R}C}R_{P}$
. Then as
$Q=\prod _{P\in Min_{R}C}R_{P}$
. Then as
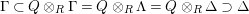 $\unicode[STIX]{x1D6E4}\subset Q\otimes _{R}\unicode[STIX]{x1D6E4}=Q\otimes _{R}\unicode[STIX]{x1D6EC}=Q\otimes _{R}\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}$
, both
$\unicode[STIX]{x1D6E4}\subset Q\otimes _{R}\unicode[STIX]{x1D6E4}=Q\otimes _{R}\unicode[STIX]{x1D6EC}=Q\otimes _{R}\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}$
, both
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6E5}$
are identified with
$\unicode[STIX]{x1D6E5}$
are identified with
![]() $Q$
-subalgebras of
$Q$
-subalgebras of
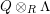 $Q\otimes _{R}\unicode[STIX]{x1D6EC}$
. As
$Q\otimes _{R}\unicode[STIX]{x1D6EC}$
. As
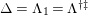 $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6EC}^{\dagger \ddagger }$
, we have a commutative diagram
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6EC}^{\dagger \ddagger }$
, we have a commutative diagram
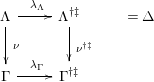
As
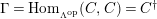 $\unicode[STIX]{x1D6E4}= Hom_{_{\unicode[STIX]{x1D6EC}^{op}}}(C,C)=C^{\dagger }$
,
$\unicode[STIX]{x1D6E4}= Hom_{_{\unicode[STIX]{x1D6EC}^{op}}}(C,C)=C^{\dagger }$
,
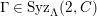 $\unicode[STIX]{x1D6E4}\in Syz_{\unicode[STIX]{x1D6EC}}(2,C)$
by Lemma 4.8. By Lemma 6.24, we have that
$\unicode[STIX]{x1D6E4}\in Syz_{\unicode[STIX]{x1D6EC}}(2,C)$
by Lemma 4.8. By Lemma 6.24, we have that
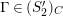 $\unicode[STIX]{x1D6E4}\in (S_{2}^{\prime })_{C}$
. Hence by Lemma 6.24 again,
$\unicode[STIX]{x1D6E4}\in (S_{2}^{\prime })_{C}$
. Hence by Lemma 6.24 again,
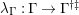 $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E4}}:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\dagger \ddagger }$
is an isomorphism. Hence
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E4}}:\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\dagger \ddagger }$
is an isomorphism. Hence
![]() $\unicode[STIX]{x1D6E5}\subset \unicode[STIX]{x1D6E4}$
. By symmetry
$\unicode[STIX]{x1D6E5}\subset \unicode[STIX]{x1D6E4}$
. By symmetry
![]() $\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E4}$
. So
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E4}$
. So
![]() $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E4}$
. With this identification,
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E4}$
. With this identification,
![]() $\unicode[STIX]{x1D6E4}$
acts on
$\unicode[STIX]{x1D6E4}$
acts on
![]() $C$
not only from left, but also from right. As the actions of
$C$
not only from left, but also from right. As the actions of
![]() $\unicode[STIX]{x1D6E4}$
extend those of
$\unicode[STIX]{x1D6E4}$
extend those of
![]() $\unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D6EC}$
,
![]() $C$
is a
$C$
is a
![]() $\unicode[STIX]{x1D6E4}$
-bimodule. Indeed, for
$\unicode[STIX]{x1D6E4}$
-bimodule. Indeed, for
![]() $a\in \unicode[STIX]{x1D6EC}$
, the left multiplication
$a\in \unicode[STIX]{x1D6EC}$
, the left multiplication
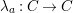 $\unicode[STIX]{x1D706}_{a}:C\rightarrow C$
(
$\unicode[STIX]{x1D706}_{a}:C\rightarrow C$
(
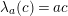 $\unicode[STIX]{x1D706}_{a}(c)=ac$
) is right
$\unicode[STIX]{x1D706}_{a}(c)=ac$
) is right
![]() $\unicode[STIX]{x1D6E4}$
-linear. So for
$\unicode[STIX]{x1D6E4}$
-linear. So for
![]() $b\in \unicode[STIX]{x1D6E4}$
,
$b\in \unicode[STIX]{x1D6E4}$
,
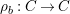 $\unicode[STIX]{x1D70C}_{b}:C\rightarrow C$
(
$\unicode[STIX]{x1D70C}_{b}:C\rightarrow C$
(
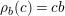 $\unicode[STIX]{x1D70C}_{b}(c)=cb$
) is left
$\unicode[STIX]{x1D70C}_{b}(c)=cb$
) is left
![]() $\unicode[STIX]{x1D6EC}$
-linear, and hence is left
$\unicode[STIX]{x1D6EC}$
-linear, and hence is left
![]() $\unicode[STIX]{x1D6E4}$
-linear.
$\unicode[STIX]{x1D6E4}$
-linear.
Theorem 6.27. Let the notation be as in (4.1), (6.4), and (4.9). Let
![]() $C$
be a
$C$
be a
![]() $2$
-canonical right
$2$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module. Then the restriction
$\unicode[STIX]{x1D6EC}$
-module. Then the restriction
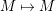 $M\mapsto M$
gives an equivalence
$M\mapsto M$
gives an equivalence
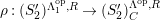 $\unicode[STIX]{x1D70C}:(S_{2}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}^{op},R}\rightarrow (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
.
$\unicode[STIX]{x1D70C}:(S_{2}^{\prime })^{\unicode[STIX]{x1D6EC}_{1}^{op},R}\rightarrow (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
.
Proof. The functor is obviously well defined, and is full and faithful by Lemma 6.12. On the other hand, given
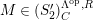 $M\in (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
, we have that
$M\in (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
, we have that
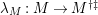 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is an isomorphism. As
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
is an isomorphism. As
![]() $M^{\dagger \ddagger }$
has a
$M^{\dagger \ddagger }$
has a
![]() $\unicode[STIX]{x1D6EC}_{1}^{op}$
-module structure which extends the
$\unicode[STIX]{x1D6EC}_{1}^{op}$
-module structure which extends the
![]() $\unicode[STIX]{x1D6EC}^{op}$
-module structure of
$\unicode[STIX]{x1D6EC}^{op}$
-module structure of
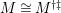 $M\cong M^{\dagger \ddagger }$
, we have that
$M\cong M^{\dagger \ddagger }$
, we have that
![]() $\unicode[STIX]{x1D70C}$
is also dense, and hence is an equivalence.◻
$\unicode[STIX]{x1D70C}$
is also dense, and hence is an equivalence.◻
Corollary 6.28. Let
![]() $C$
be a
$C$
be a
![]() $2$
-canonical
$2$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule. Then the restriction
$\unicode[STIX]{x1D6EC}$
-bimodule. Then the restriction
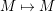 $M\mapsto M$
gives an equivalence
$M\mapsto M$
gives an equivalence
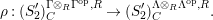 $$\begin{eqnarray}\unicode[STIX]{x1D70C}:(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E4}^{op},R}\rightarrow (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E4}^{op},R}\rightarrow (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}.\end{eqnarray}$$
Proof.
![]() $\unicode[STIX]{x1D70C}$
is well defined, and is obviously faithful. If
$\unicode[STIX]{x1D70C}$
is well defined, and is obviously faithful. If
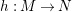 $h:M\rightarrow N$
is a morphism of
$h:M\rightarrow N$
is a morphism of
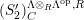 $(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
between objects of
$(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
between objects of
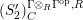 $(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E4}^{op},R}$
, then
$(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6E4}\otimes _{R}\unicode[STIX]{x1D6E4}^{op},R}$
, then
![]() $h$
is
$h$
is
![]() $\unicode[STIX]{x1D6E4}$
-linear
$\unicode[STIX]{x1D6E4}$
-linear
![]() $\unicode[STIX]{x1D6E4}^{op}$
-linear by Theorem 6.27 (note that
$\unicode[STIX]{x1D6E4}^{op}$
-linear by Theorem 6.27 (note that
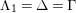 $\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E4}$
here). Hence
$\unicode[STIX]{x1D6EC}_{1}=\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E4}$
here). Hence
![]() $\unicode[STIX]{x1D70C}$
is full.
$\unicode[STIX]{x1D70C}$
is full.
Let
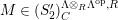 $M\in (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
, the left (resp. right)
$M\in (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op},R}$
, the left (resp. right)
![]() $\unicode[STIX]{x1D6EC}$
-module structure of
$\unicode[STIX]{x1D6EC}$
-module structure of
![]() $M$
is extendable to that of a left (resp. right)
$M$
is extendable to that of a left (resp. right)
![]() $\unicode[STIX]{x1D6E4}$
-module structure by Theorem 6.27. It remains to show that these structures make
$\unicode[STIX]{x1D6E4}$
-module structure by Theorem 6.27. It remains to show that these structures make
![]() $M$
a
$M$
a
![]() $\unicode[STIX]{x1D6E4}$
-bimodule. Let
$\unicode[STIX]{x1D6E4}$
-bimodule. Let
![]() $a\in \unicode[STIX]{x1D6EC}$
. Then
$a\in \unicode[STIX]{x1D6EC}$
. Then
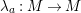 $\unicode[STIX]{x1D706}_{a}:M\rightarrow M$
given by
$\unicode[STIX]{x1D706}_{a}:M\rightarrow M$
given by
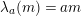 $\unicode[STIX]{x1D706}_{a}(m)=am$
is a right
$\unicode[STIX]{x1D706}_{a}(m)=am$
is a right
![]() $\unicode[STIX]{x1D6EC}$
-linear, and hence is right
$\unicode[STIX]{x1D6EC}$
-linear, and hence is right
![]() $\unicode[STIX]{x1D6E4}$
-linear. So for
$\unicode[STIX]{x1D6E4}$
-linear. So for
![]() $b\in \unicode[STIX]{x1D6E4}$
,
$b\in \unicode[STIX]{x1D6E4}$
,
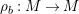 $\unicode[STIX]{x1D70C}_{b}:M\rightarrow M$
given by
$\unicode[STIX]{x1D70C}_{b}:M\rightarrow M$
given by
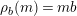 $\unicode[STIX]{x1D70C}_{b}(m)=mb$
is left
$\unicode[STIX]{x1D70C}_{b}(m)=mb$
is left
![]() $\unicode[STIX]{x1D6EC}$
-linear, and hence is left
$\unicode[STIX]{x1D6EC}$
-linear, and hence is left
![]() $\unicode[STIX]{x1D6E4}$
-linear, as desired.◻
$\unicode[STIX]{x1D6E4}$
-linear, as desired.◻
Proposition 6.29. Let
![]() $C$
be a
$C$
be a
![]() $2$
-canonical right
$2$
-canonical right
![]() $\unicode[STIX]{x1D6EC}$
-module. Then
$\unicode[STIX]{x1D6EC}$
-module. Then
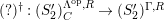 $(?)^{\dagger }:(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}\rightarrow (S_{2}^{\prime })^{\unicode[STIX]{x1D6E4},R}$
and
$(?)^{\dagger }:(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}\rightarrow (S_{2}^{\prime })^{\unicode[STIX]{x1D6E4},R}$
and
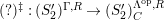 $(?)^{\ddagger }:(S_{2}^{\prime })^{\unicode[STIX]{x1D6E4},R}\rightarrow (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
give a contravariant equivalence.
$(?)^{\ddagger }:(S_{2}^{\prime })^{\unicode[STIX]{x1D6E4},R}\rightarrow (S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
give a contravariant equivalence.
Proof. As we know that
![]() $(?)^{\dagger }$
and
$(?)^{\dagger }$
and
![]() $(?)^{\ddagger }$
are contravariant adjoint each other, it suffices to show that the unit
$(?)^{\ddagger }$
are contravariant adjoint each other, it suffices to show that the unit
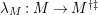 $\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
and the (co-)unit
$\unicode[STIX]{x1D706}_{M}:M\rightarrow M^{\dagger \ddagger }$
and the (co-)unit
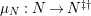 $\unicode[STIX]{x1D707}_{N}:N\rightarrow N^{\ddagger \dagger }$
are isomorphisms.
$\unicode[STIX]{x1D707}_{N}:N\rightarrow N^{\ddagger \dagger }$
are isomorphisms.
![]() $\unicode[STIX]{x1D706}_{M}$
is an isomorphism by Lemma 6.24. Note that
$\unicode[STIX]{x1D706}_{M}$
is an isomorphism by Lemma 6.24. Note that
![]() $C$
is a
$C$
is a
![]() $2$
-canonical left
$2$
-canonical left
![]() $\unicode[STIX]{x1D6E4}$
-module by Lemma 6.23. So
$\unicode[STIX]{x1D6E4}$
-module by Lemma 6.23. So
![]() $\unicode[STIX]{x1D707}_{N}$
is an isomorphism by Lemma 6.24 applied to the right
$\unicode[STIX]{x1D707}_{N}$
is an isomorphism by Lemma 6.24 applied to the right
![]() $\unicode[STIX]{x1D6E4}^{op}$
-module
$\unicode[STIX]{x1D6E4}^{op}$
-module
![]() $C$
.◻
$C$
.◻
Corollary 6.30. Let
![]() $C$
be a
$C$
be a
![]() $2$
-canonical
$2$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule. Then
$\unicode[STIX]{x1D6EC}$
-bimodule. Then
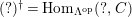 $(?)^{\dagger }= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C)$
and
$(?)^{\dagger }= Hom_{\unicode[STIX]{x1D6EC}^{op}}(?,C)$
and
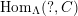 $Hom_{\unicode[STIX]{x1D6EC}}(?,C)$
give a contravariant equivalence between
$Hom_{\unicode[STIX]{x1D6EC}}(?,C)$
give a contravariant equivalence between
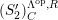 $(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
and
$(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}^{op},R}$
and
![]() $(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC},R}$
. They also give a duality of
$(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC},R}$
. They also give a duality of
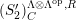 $(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes \unicode[STIX]{x1D6EC}^{op},R}$
.
$(S_{2}^{\prime })_{C}^{\unicode[STIX]{x1D6EC}\otimes \unicode[STIX]{x1D6EC}^{op},R}$
.
7 Noncommutative Aoyama’s theorem
Lemma 7.1. Let
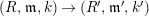 $(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings.
$(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings.
-
(1) Let
 $M$
be a
$M$
be a
 $\unicode[STIX]{x1D6EC}$
-bimodule such that
$\unicode[STIX]{x1D6EC}$
-bimodule such that
 $M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
$M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
 $\unicode[STIX]{x1D6EC}^{\prime }:=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
as a
$\unicode[STIX]{x1D6EC}^{\prime }:=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
as a
 $\unicode[STIX]{x1D6EC}^{\prime }$
-bimodule. Then
$\unicode[STIX]{x1D6EC}^{\prime }$
-bimodule. Then
 $M\cong \unicode[STIX]{x1D6EC}$
as a
$M\cong \unicode[STIX]{x1D6EC}$
as a
 $\unicode[STIX]{x1D6EC}$
-bimodule.
$\unicode[STIX]{x1D6EC}$
-bimodule. -
(2) Let
 $M$
be a right
$M$
be a right
 $\unicode[STIX]{x1D6EC}$
module such that
$\unicode[STIX]{x1D6EC}$
module such that
 $M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
$M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
 $\unicode[STIX]{x1D6EC}^{\prime }:=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
as a right
$\unicode[STIX]{x1D6EC}^{\prime }:=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
as a right
 $\unicode[STIX]{x1D6EC}^{\prime }$
-module. Then
$\unicode[STIX]{x1D6EC}^{\prime }$
-module. Then
 $M\cong \unicode[STIX]{x1D6EC}$
as a right
$M\cong \unicode[STIX]{x1D6EC}$
as a right
 $\unicode[STIX]{x1D6EC}$
-module.
$\unicode[STIX]{x1D6EC}$
-module.
Proof. Taking the completion, we may assume that both
![]() $R$
and
$R$
and
![]() $R^{\prime }$
are complete. Let
$R^{\prime }$
are complete. Let
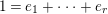 $1=e_{1}+\cdots +e_{r}$
be the decomposition of
$1=e_{1}+\cdots +e_{r}$
be the decomposition of
![]() $1$
into the mutually orthogonal primitive idempotents of the center
$1$
into the mutually orthogonal primitive idempotents of the center
![]() $S$
of
$S$
of
![]() $\unicode[STIX]{x1D6EC}$
. Then replacing
$\unicode[STIX]{x1D6EC}$
. Then replacing
![]() $R$
by
$R$
by
![]() $Se_{i}$
,
$Se_{i}$
,
![]() $\unicode[STIX]{x1D6EC}$
by
$\unicode[STIX]{x1D6EC}$
by
![]() $\unicode[STIX]{x1D6EC}e_{i}$
, and
$\unicode[STIX]{x1D6EC}e_{i}$
, and
![]() $R^{\prime }$
by the local ring of
$R^{\prime }$
by the local ring of
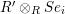 $R^{\prime }\otimes _{R}Se_{i}$
at any maximal ideal, we may further assume that
$R^{\prime }\otimes _{R}Se_{i}$
at any maximal ideal, we may further assume that
![]() $S=R$
. This is equivalent to say that
$S=R$
. This is equivalent to say that
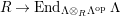 $R\rightarrow End_{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}\unicode[STIX]{x1D6EC}$
is isomorphic. So
$R\rightarrow End_{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}\unicode[STIX]{x1D6EC}$
is isomorphic. So
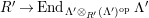 $R^{\prime }\rightarrow End_{\unicode[STIX]{x1D6EC}^{\prime }\otimes _{R^{\prime }}(\unicode[STIX]{x1D6EC}^{\prime })^{op}}\unicode[STIX]{x1D6EC}^{\prime }$
is also isomorphic, and hence the center of
$R^{\prime }\rightarrow End_{\unicode[STIX]{x1D6EC}^{\prime }\otimes _{R^{\prime }}(\unicode[STIX]{x1D6EC}^{\prime })^{op}}\unicode[STIX]{x1D6EC}^{\prime }$
is also isomorphic, and hence the center of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
is
$\unicode[STIX]{x1D6EC}^{\prime }$
is
![]() $R^{\prime }$
.
$R^{\prime }$
.
(1) Let
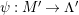 $\unicode[STIX]{x1D713}:M^{\prime }\rightarrow \unicode[STIX]{x1D6EC}^{\prime }$
be an isomorphism. Then we can write
$\unicode[STIX]{x1D713}:M^{\prime }\rightarrow \unicode[STIX]{x1D6EC}^{\prime }$
be an isomorphism. Then we can write
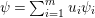 $\unicode[STIX]{x1D713}=\sum _{i=1}^{m}u_{i}\unicode[STIX]{x1D713}_{i}$
with
$\unicode[STIX]{x1D713}=\sum _{i=1}^{m}u_{i}\unicode[STIX]{x1D713}_{i}$
with
![]() $u_{i}\in R^{\prime }$
and
$u_{i}\in R^{\prime }$
and
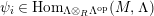 $\unicode[STIX]{x1D713}_{i}\in Hom_{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}(M,\unicode[STIX]{x1D6EC})$
. Also, we can write
$\unicode[STIX]{x1D713}_{i}\in Hom_{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}(M,\unicode[STIX]{x1D6EC})$
. Also, we can write
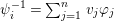 $\unicode[STIX]{x1D713}_{i}^{-1}=\sum _{j=1}^{n}v_{j}\unicode[STIX]{x1D711}_{j}$
with
$\unicode[STIX]{x1D713}_{i}^{-1}=\sum _{j=1}^{n}v_{j}\unicode[STIX]{x1D711}_{j}$
with
![]() $v_{j}\in R^{\prime }$
and
$v_{j}\in R^{\prime }$
and
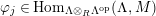 $\unicode[STIX]{x1D711}_{j}\in Hom_{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},M)$
. As
$\unicode[STIX]{x1D711}_{j}\in Hom_{\unicode[STIX]{x1D6EC}\otimes _{R}\unicode[STIX]{x1D6EC}^{op}}(\unicode[STIX]{x1D6EC},M)$
. As
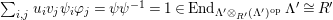 $\sum _{i,j}u_{i}v_{j}\unicode[STIX]{x1D713}_{i}\unicode[STIX]{x1D711}_{j}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D713}^{-1}=1\in End_{\unicode[STIX]{x1D6EC}^{\prime }\otimes _{R^{\prime }}(\unicode[STIX]{x1D6EC}^{\prime })^{op}}\unicode[STIX]{x1D6EC}^{\prime }\cong R^{\prime }$
and
$\sum _{i,j}u_{i}v_{j}\unicode[STIX]{x1D713}_{i}\unicode[STIX]{x1D711}_{j}=\unicode[STIX]{x1D713}\unicode[STIX]{x1D713}^{-1}=1\in End_{\unicode[STIX]{x1D6EC}^{\prime }\otimes _{R^{\prime }}(\unicode[STIX]{x1D6EC}^{\prime })^{op}}\unicode[STIX]{x1D6EC}^{\prime }\cong R^{\prime }$
and
![]() $R^{\prime }$
is local, there exists some
$R^{\prime }$
is local, there exists some
![]() $i,j$
such that
$i,j$
such that
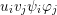 $u_{i}v_{j}\unicode[STIX]{x1D713}_{i}\unicode[STIX]{x1D711}_{j}$
is an automorphism of
$u_{i}v_{j}\unicode[STIX]{x1D713}_{i}\unicode[STIX]{x1D711}_{j}$
is an automorphism of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
. Then
$\unicode[STIX]{x1D6EC}^{\prime }$
. Then
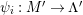 $\unicode[STIX]{x1D713}_{i}:M^{\prime }\rightarrow \unicode[STIX]{x1D6EC}^{\prime }$
is also an isomorphism. By faithful flatness,
$\unicode[STIX]{x1D713}_{i}:M^{\prime }\rightarrow \unicode[STIX]{x1D6EC}^{\prime }$
is also an isomorphism. By faithful flatness,
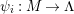 $\unicode[STIX]{x1D713}_{i}:M\rightarrow \unicode[STIX]{x1D6EC}$
is an isomorphism.
$\unicode[STIX]{x1D713}_{i}:M\rightarrow \unicode[STIX]{x1D6EC}$
is an isomorphism.
(2) It is easy to see that
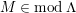 $M\in mod\unicode[STIX]{x1D6EC}$
is projective. So replacing
$M\in mod\unicode[STIX]{x1D6EC}$
is projective. So replacing
![]() $\unicode[STIX]{x1D6EC}$
by
$\unicode[STIX]{x1D6EC}$
by
![]() $\unicode[STIX]{x1D6EC}/J$
, where
$\unicode[STIX]{x1D6EC}/J$
, where
![]() $J$
is the radical of
$J$
is the radical of
![]() $\unicode[STIX]{x1D6EC}$
, and changing
$\unicode[STIX]{x1D6EC}$
, and changing
![]() $R$
and
$R$
and
![]() $R^{\prime }$
as above, we may assume that
$R^{\prime }$
as above, we may assume that
![]() $R$
is a field and
$R$
is a field and
![]() $\unicode[STIX]{x1D6EC}$
is central simple. Then there is only one simple right
$\unicode[STIX]{x1D6EC}$
is central simple. Then there is only one simple right
![]() $\unicode[STIX]{x1D6EC}$
-module, and
$\unicode[STIX]{x1D6EC}$
-module, and
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D6EC}$
are direct sums of copies of it. As
$\unicode[STIX]{x1D6EC}$
are direct sums of copies of it. As
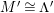 $M^{\prime }\cong \unicode[STIX]{x1D6EC}^{\prime }$
, by dimension counting, the number of copies are equal, and hence
$M^{\prime }\cong \unicode[STIX]{x1D6EC}^{\prime }$
, by dimension counting, the number of copies are equal, and hence
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D6EC}$
are isomorphic.◻
$\unicode[STIX]{x1D6EC}$
are isomorphic.◻
Lemma 7.2. Let
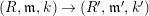 $(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings.
$(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings.
-
(1) Let
 $C$
be a
$C$
be a
 $2$
-canonical bimodule of
$2$
-canonical bimodule of
 $\unicode[STIX]{x1D6EC}$
over
$\unicode[STIX]{x1D6EC}$
over
 $R$
. Let
$R$
. Let
 $M$
be a
$M$
be a
 $\unicode[STIX]{x1D6EC}$
-bimodule such that
$\unicode[STIX]{x1D6EC}$
-bimodule such that
 $M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
$M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
 $C^{\prime }:=R^{\prime }\otimes _{R}C$
as a
$C^{\prime }:=R^{\prime }\otimes _{R}C$
as a
 $\unicode[STIX]{x1D6EC}^{\prime }$
-bimodule. Then
$\unicode[STIX]{x1D6EC}^{\prime }$
-bimodule. Then
 $M\cong C$
as a
$M\cong C$
as a
 $\unicode[STIX]{x1D6EC}$
-bimodule.
$\unicode[STIX]{x1D6EC}$
-bimodule. -
(2) Let
 $C$
be a
$C$
be a
 $2$
-canonical right
$2$
-canonical right
 $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
 $R$
. Let
$R$
. Let
 $M$
be a right
$M$
be a right
 $\unicode[STIX]{x1D6EC}$
-module such that
$\unicode[STIX]{x1D6EC}$
-module such that
 $M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
$M^{\prime }:=R^{\prime }\otimes _{R}M$
is isomorphic to
 $C^{\prime }:=R^{\prime }\otimes _{R}C$
as a right
$C^{\prime }:=R^{\prime }\otimes _{R}C$
as a right
 $\unicode[STIX]{x1D6EC}^{\prime }$
-module. Then
$\unicode[STIX]{x1D6EC}^{\prime }$
-module. Then
 $M\cong C$
as a right
$M\cong C$
as a right
 $\unicode[STIX]{x1D6EC}$
-module.
$\unicode[STIX]{x1D6EC}$
-module.
Proof. (1) As
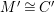 $M^{\prime }\cong C^{\prime }$
and
$M^{\prime }\cong C^{\prime }$
and
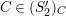 $C\in (S_{2}^{\prime })_{C}$
, it is easy to see that
$C\in (S_{2}^{\prime })_{C}$
, it is easy to see that
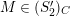 $M\in (S_{2}^{\prime })_{C}$
. Hence
$M\in (S_{2}^{\prime })_{C}$
. Hence
![]() $M$
is a
$M$
is a
![]() $\unicode[STIX]{x1D6E4}$
-bimodule, where
$\unicode[STIX]{x1D6E4}$
-bimodule, where
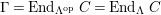 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C= End_{\unicode[STIX]{x1D6EC}}C$
; see (6.26) and Corollary 6.28. Note that
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C= End_{\unicode[STIX]{x1D6EC}}C$
; see (6.26) and Corollary 6.28. Note that
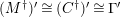 $(M^{\dagger })^{\prime }\cong (C^{\dagger })^{\prime }\cong \unicode[STIX]{x1D6E4}^{\prime }$
as
$(M^{\dagger })^{\prime }\cong (C^{\dagger })^{\prime }\cong \unicode[STIX]{x1D6E4}^{\prime }$
as
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
-bimodules. By Lemma 7.1(1), we have that
$\unicode[STIX]{x1D6E4}^{\prime }$
-bimodules. By Lemma 7.1(1), we have that
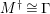 $M^{\dagger }\cong \unicode[STIX]{x1D6E4}$
as a
$M^{\dagger }\cong \unicode[STIX]{x1D6E4}$
as a
![]() $\unicode[STIX]{x1D6E4}$
-bimodule. Hence
$\unicode[STIX]{x1D6E4}$
-bimodule. Hence
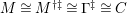 $M\cong M^{\dagger \ddagger }\cong \unicode[STIX]{x1D6E4}^{\ddagger }\cong C$
.
$M\cong M^{\dagger \ddagger }\cong \unicode[STIX]{x1D6E4}^{\ddagger }\cong C$
.
(2) As
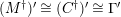 $(M^{\dagger })^{\prime }\cong (C^{\dagger })^{\prime }\cong \unicode[STIX]{x1D6E4}^{\prime }$
as
$(M^{\dagger })^{\prime }\cong (C^{\dagger })^{\prime }\cong \unicode[STIX]{x1D6E4}^{\prime }$
as
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
-modules,
$\unicode[STIX]{x1D6E4}^{\prime }$
-modules,
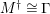 $M^{\dagger }\cong \unicode[STIX]{x1D6E4}$
as
$M^{\dagger }\cong \unicode[STIX]{x1D6E4}$
as
![]() $\unicode[STIX]{x1D6E4}$
-modules by Lemma 7.1(2). Hence
$\unicode[STIX]{x1D6E4}$
-modules by Lemma 7.1(2). Hence
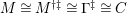 $M\cong M^{\dagger \ddagger }\cong \unicode[STIX]{x1D6E4}^{\ddagger }\cong C$
.◻
$M\cong M^{\dagger \ddagger }\cong \unicode[STIX]{x1D6E4}^{\ddagger }\cong C$
.◻
Proposition 7.3. Let
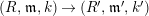 $(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings. Let
$(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings. Let
![]() $M$
be a right
$M$
be a right
![]() $\unicode[STIX]{x1D6EC}$
-module. Assume that
$\unicode[STIX]{x1D6EC}$
-module. Assume that
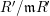 $R^{\prime }/\mathfrak{m}R^{\prime }$
is zero-dimensional, and
$R^{\prime }/\mathfrak{m}R^{\prime }$
is zero-dimensional, and
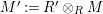 $M^{\prime }:=R^{\prime }\otimes _{R}M$
is the right canonical module of
$M^{\prime }:=R^{\prime }\otimes _{R}M$
is the right canonical module of
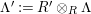 $\unicode[STIX]{x1D6EC}^{\prime }:=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
. If
$\unicode[STIX]{x1D6EC}^{\prime }:=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
. If
![]() $\unicode[STIX]{x1D6EC}\neq 0$
, then
$\unicode[STIX]{x1D6EC}\neq 0$
, then
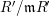 $R^{\prime }/\mathfrak{m}R^{\prime }$
is Gorenstein.
$R^{\prime }/\mathfrak{m}R^{\prime }$
is Gorenstein.
Proof. We may assume that both
![]() $R$
and
$R$
and
![]() $R^{\prime }$
are complete. Replacing
$R^{\prime }$
are complete. Replacing
![]() $R$
by
$R$
by
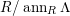 $R/ann_{R}\unicode[STIX]{x1D6EC}$
and
$R/ann_{R}\unicode[STIX]{x1D6EC}$
and
![]() $R^{\prime }$
by
$R^{\prime }$
by
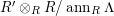 $R^{\prime }\otimes _{R}R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
$R^{\prime }\otimes _{R}R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
![]() $\unicode[STIX]{x1D6EC}$
is a faithful
$\unicode[STIX]{x1D6EC}$
is a faithful
![]() $R$
-module. Let
$R$
-module. Let
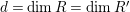 $d=\dim R=\dim R^{\prime }$
. Note that
$d=\dim R=\dim R^{\prime }$
. Note that
![]() $M$
is a finite
$M$
is a finite
![]() $R$
-module.
$R$
-module.
Then
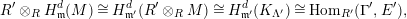 $$\begin{eqnarray}R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)\cong H_{\mathfrak{ m}^{\prime }}^{d}(R^{\prime }\otimes _{R}M)\cong H_{\mathfrak{m}^{\prime }}^{d}(K_{\unicode[STIX]{x1D6EC}^{\prime }})\cong Hom_{R^{\prime }}(\unicode[STIX]{x1D6E4}^{\prime },E^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)\cong H_{\mathfrak{ m}^{\prime }}^{d}(R^{\prime }\otimes _{R}M)\cong H_{\mathfrak{m}^{\prime }}^{d}(K_{\unicode[STIX]{x1D6EC}^{\prime }})\cong Hom_{R^{\prime }}(\unicode[STIX]{x1D6E4}^{\prime },E^{\prime }),\end{eqnarray}$$
where
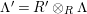 $\unicode[STIX]{x1D6EC}^{\prime }=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D6EC}^{\prime }=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
,
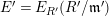 $E^{\prime }=E_{R^{\prime }}(R^{\prime }/\mathfrak{m}^{\prime })$
is the injective hull of the residue field,
$E^{\prime }=E_{R^{\prime }}(R^{\prime }/\mathfrak{m}^{\prime })$
is the injective hull of the residue field,
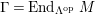 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}M$
,
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}M$
,
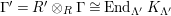 $\unicode[STIX]{x1D6E4}^{\prime }=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6E4}\cong End_{\unicode[STIX]{x1D6EC}^{\prime }}K_{\unicode[STIX]{x1D6EC}^{\prime }}$
, and the isomorphisms are those of
$\unicode[STIX]{x1D6E4}^{\prime }=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6E4}\cong End_{\unicode[STIX]{x1D6EC}^{\prime }}K_{\unicode[STIX]{x1D6EC}^{\prime }}$
, and the isomorphisms are those of
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
-modules. The last isomorphism is by (5.19). So
$\unicode[STIX]{x1D6E4}^{\prime }$
-modules. The last isomorphism is by (5.19). So
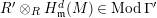 $R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)\in Mod\unicode[STIX]{x1D6E4}^{\prime }$
is injective. Considering the spectral sequence
$R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)\in Mod\unicode[STIX]{x1D6E4}^{\prime }$
is injective. Considering the spectral sequence
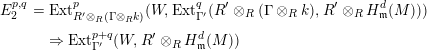 $$\begin{eqnarray}\displaystyle E_{2}^{p,q} & = & \displaystyle Ext_{R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k)}^{p}(W,Ext_{\unicode[STIX]{x1D6E4}^{\prime }}^{q}(R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k),R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)))\nonumber\\ \displaystyle & & \displaystyle \Rightarrow Ext_{\unicode[STIX]{x1D6E4}^{\prime }}^{p+q}(W,R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{2}^{p,q} & = & \displaystyle Ext_{R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k)}^{p}(W,Ext_{\unicode[STIX]{x1D6E4}^{\prime }}^{q}(R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k),R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)))\nonumber\\ \displaystyle & & \displaystyle \Rightarrow Ext_{\unicode[STIX]{x1D6E4}^{\prime }}^{p+q}(W,R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M))\nonumber\end{eqnarray}$$
for
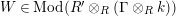 $W\in Mod(R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k))$
,
$W\in Mod(R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k))$
,
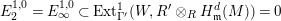 $E_{2}^{1,0}=E_{\infty }^{1,0}\subset Ext_{\unicode[STIX]{x1D6E4}^{\prime }}^{1}(W,R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M))=0$
by the injectivity of
$E_{2}^{1,0}=E_{\infty }^{1,0}\subset Ext_{\unicode[STIX]{x1D6E4}^{\prime }}^{1}(W,R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M))=0$
by the injectivity of
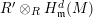 $R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)$
. It follows that
$R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M)$
. It follows that
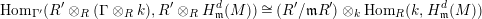 $$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6E4}^{\prime }}(R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k),R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M))\cong (R^{\prime }/\mathfrak{m}R^{\prime })\otimes _{k} Hom_{R}(k,H_{\mathfrak{m}}^{d}(M))\end{eqnarray}$$
$$\begin{eqnarray}Hom_{\unicode[STIX]{x1D6E4}^{\prime }}(R^{\prime }\otimes _{R}(\unicode[STIX]{x1D6E4}\otimes _{R}k),R^{\prime }\otimes _{R}H_{\mathfrak{m}}^{d}(M))\cong (R^{\prime }/\mathfrak{m}R^{\prime })\otimes _{k} Hom_{R}(k,H_{\mathfrak{m}}^{d}(M))\end{eqnarray}$$
is an injective
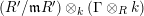 $(R^{\prime }/\mathfrak{m}R^{\prime })\otimes _{k}(\unicode[STIX]{x1D6E4}\otimes _{R}k)$
-module. However, as an
$(R^{\prime }/\mathfrak{m}R^{\prime })\otimes _{k}(\unicode[STIX]{x1D6E4}\otimes _{R}k)$
-module. However, as an
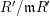 $R^{\prime }/\mathfrak{m}R^{\prime }$
-module, this is a free module. Also, this module must be an injective
$R^{\prime }/\mathfrak{m}R^{\prime }$
-module, this is a free module. Also, this module must be an injective
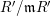 $R^{\prime }/\mathfrak{m}R^{\prime }$
-module, and hence
$R^{\prime }/\mathfrak{m}R^{\prime }$
-module, and hence
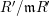 $R^{\prime }/\mathfrak{m}R^{\prime }$
must be Gorenstein.◻
$R^{\prime }/\mathfrak{m}R^{\prime }$
must be Gorenstein.◻
Lemma 7.4. Let
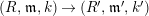 $(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings such that
$(R,\mathfrak{m},k)\rightarrow (R^{\prime },\mathfrak{m}^{\prime },k^{\prime })$
be a flat local homomorphism between Noetherian local rings such that
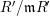 $R^{\prime }/\mathfrak{m}R^{\prime }$
is Gorenstein. Assume that the canonical module
$R^{\prime }/\mathfrak{m}R^{\prime }$
is Gorenstein. Assume that the canonical module
![]() $K_{\unicode[STIX]{x1D6EC}}$
of
$K_{\unicode[STIX]{x1D6EC}}$
of
![]() $\unicode[STIX]{x1D6EC}$
exists. Then
$\unicode[STIX]{x1D6EC}$
exists. Then
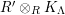 $R^{\prime }\otimes _{R}K_{\unicode[STIX]{x1D6EC}}$
is the canonical module of
$R^{\prime }\otimes _{R}K_{\unicode[STIX]{x1D6EC}}$
is the canonical module of
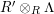 $R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
.
$R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
.
Proof. We may assume that both
![]() $R$
and
$R$
and
![]() $R^{\prime }$
are complete and
$R^{\prime }$
are complete and
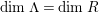 $\dim \unicode[STIX]{x1D6EC}=\dim R$
. Let
$\dim \unicode[STIX]{x1D6EC}=\dim R$
. Let
![]() $\mathbb{I}$
be the normalized dualizing complex of
$\mathbb{I}$
be the normalized dualizing complex of
![]() $R$
. Then
$R$
. Then
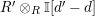 $R^{\prime }\otimes _{R}\mathbb{I}[d^{\prime }-d]$
is a normalized dualizing complex of
$R^{\prime }\otimes _{R}\mathbb{I}[d^{\prime }-d]$
is a normalized dualizing complex of
![]() $R^{\prime }$
, where
$R^{\prime }$
, where
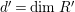 $d^{\prime }=\dim R^{\prime }$
and
$d^{\prime }=\dim R^{\prime }$
and
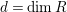 $d=\dim R$
, since
$d=\dim R$
, since
![]() $R\rightarrow R^{\prime }$
is a flat local homomorphism with the
$R\rightarrow R^{\prime }$
is a flat local homomorphism with the
![]() $d^{\prime }-d$
-dimensional Gorenstein closed fiber; see [Reference Avramov and FoxbyAvF, (5.1)] (the definition of a normalized dualizing complex in [Reference Avramov and FoxbyAvF] is different from ours. We follow the one in [Reference HartshorneHart, Chapter V]). So
$d^{\prime }-d$
-dimensional Gorenstein closed fiber; see [Reference Avramov and FoxbyAvF, (5.1)] (the definition of a normalized dualizing complex in [Reference Avramov and FoxbyAvF] is different from ours. We follow the one in [Reference HartshorneHart, Chapter V]). So
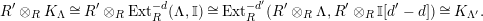 $$\begin{eqnarray}R^{\prime }\otimes _{R}K_{\unicode[STIX]{x1D6EC}}\cong R^{\prime }\otimes _{R} Ext_{R}^{-d}(\unicode[STIX]{x1D6EC},\mathbb{I})\cong Ext_{R}^{-d^{\prime }}(R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC},R^{\prime }\otimes _{R}\mathbb{I}[d^{\prime }-d])\cong K_{\unicode[STIX]{x1D6EC}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}R^{\prime }\otimes _{R}K_{\unicode[STIX]{x1D6EC}}\cong R^{\prime }\otimes _{R} Ext_{R}^{-d}(\unicode[STIX]{x1D6EC},\mathbb{I})\cong Ext_{R}^{-d^{\prime }}(R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC},R^{\prime }\otimes _{R}\mathbb{I}[d^{\prime }-d])\cong K_{\unicode[STIX]{x1D6EC}^{\prime }}.\end{eqnarray}$$
◻
Theorem 7.5. ((Noncommutative Aoyama’s theorem) cf. [Reference AoyamaAoy , Theorem 4.2])
Let
 $(R,\mathfrak{m})\rightarrow (R^{\prime },\mathfrak{m}^{\prime })$
be a flat local homomorphism between Noetherian local rings, and
$(R,\mathfrak{m})\rightarrow (R^{\prime },\mathfrak{m}^{\prime })$
be a flat local homomorphism between Noetherian local rings, and
![]() $\unicode[STIX]{x1D6EC}$
a module-finite
$\unicode[STIX]{x1D6EC}$
a module-finite
![]() $R$
-algebra.
$R$
-algebra.
-
(1) If
 $M$
is a
$M$
is a
 $\unicode[STIX]{x1D6EC}$
-bimodule and
$\unicode[STIX]{x1D6EC}$
-bimodule and
 $M^{\prime }=R^{\prime }\otimes _{R}M$
is the canonical module of
$M^{\prime }=R^{\prime }\otimes _{R}M$
is the canonical module of
 $\unicode[STIX]{x1D6EC}^{\prime }=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
, then
$\unicode[STIX]{x1D6EC}^{\prime }=R^{\prime }\otimes _{R}\unicode[STIX]{x1D6EC}$
, then
 $M$
is the canonical module of
$M$
is the canonical module of
 $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
. -
(2) If
 $M$
is a right
$M$
is a right
 $\unicode[STIX]{x1D6EC}$
-module such that
$\unicode[STIX]{x1D6EC}$
-module such that
 $M^{\prime }$
is the right canonical module of
$M^{\prime }$
is the right canonical module of
 $\unicode[STIX]{x1D6EC}^{\prime }$
, then
$\unicode[STIX]{x1D6EC}^{\prime }$
, then
 $M$
is the right canonical module of
$M$
is the right canonical module of
 $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Proof. We may assume that both
![]() $R$
and
$R$
and
![]() $R^{\prime }$
are complete. Then the canonical module exists, and the localization of a canonical module is a canonical module, and hence we may localize
$R^{\prime }$
are complete. Then the canonical module exists, and the localization of a canonical module is a canonical module, and hence we may localize
![]() $R^{\prime }$
by a minimal element of
$R^{\prime }$
by a minimal element of
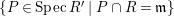 $\{P\in SpecR^{\prime }\mid P\cap R=\mathfrak{m}\}$
, and take the completion again, we may further assume that the fiber ring
$\{P\in SpecR^{\prime }\mid P\cap R=\mathfrak{m}\}$
, and take the completion again, we may further assume that the fiber ring
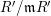 $R^{\prime }/\mathfrak{m}R^{\prime }$
is zero-dimensional. Then
$R^{\prime }/\mathfrak{m}R^{\prime }$
is zero-dimensional. Then
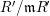 $R^{\prime }/\mathfrak{m}R^{\prime }$
is Gorenstein by Proposition 7.3. Then by Lemma 7.4,
$R^{\prime }/\mathfrak{m}R^{\prime }$
is Gorenstein by Proposition 7.3. Then by Lemma 7.4,
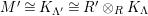 $M^{\prime }\cong K_{\unicode[STIX]{x1D6EC}^{\prime }}\cong R^{\prime }\otimes _{R}K_{\unicode[STIX]{x1D6EC}}$
. By Lemma 7.2,
$M^{\prime }\cong K_{\unicode[STIX]{x1D6EC}^{\prime }}\cong R^{\prime }\otimes _{R}K_{\unicode[STIX]{x1D6EC}}$
. By Lemma 7.2,
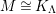 $M\cong K_{\unicode[STIX]{x1D6EC}}$
. In (1), the isomorphisms are those of bimodules, while in (2), they are of right modules. The proofs of (1) and (2) are complete.◻
$M\cong K_{\unicode[STIX]{x1D6EC}}$
. In (1), the isomorphisms are those of bimodules, while in (2), they are of right modules. The proofs of (1) and (2) are complete.◻
Corollary 7.6. Let
![]() $(R,\mathfrak{m})$
be a Noetherian local ring, and assume that
$(R,\mathfrak{m})$
be a Noetherian local ring, and assume that
![]() $K$
is the canonical (resp. right canonical) module of
$K$
is the canonical (resp. right canonical) module of
![]() $\unicode[STIX]{x1D6EC}$
. If
$\unicode[STIX]{x1D6EC}$
. If
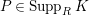 $P\in Supp_{R}K$
, then the localization
$P\in Supp_{R}K$
, then the localization
![]() $K_{P}$
is the canonical (resp. right canonical) module of
$K_{P}$
is the canonical (resp. right canonical) module of
![]() $\unicode[STIX]{x1D6EC}_{P}$
. In particular,
$\unicode[STIX]{x1D6EC}_{P}$
. In particular,
![]() $K$
is a semicanonical bimodule (resp. right module), and hence is
$K$
is a semicanonical bimodule (resp. right module), and hence is
![]() $2$
-canonical over
$2$
-canonical over
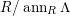 $R/ann_{R}\unicode[STIX]{x1D6EC}$
.
$R/ann_{R}\unicode[STIX]{x1D6EC}$
.
Proof. Let
![]() $Q$
be a prime ideal of
$Q$
be a prime ideal of
![]() $\hat{R}$
lying over
$\hat{R}$
lying over
![]() $P$
. Then
$P$
. Then
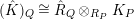 $(\hat{K})_{Q}\cong \hat{R}_{Q}\otimes _{R_{P}}K_{P}$
is nonzero by assumption, and hence is the canonical (resp. right canonical) module of
$(\hat{K})_{Q}\cong \hat{R}_{Q}\otimes _{R_{P}}K_{P}$
is nonzero by assumption, and hence is the canonical (resp. right canonical) module of
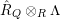 $\hat{R}_{Q}\otimes _{R}\unicode[STIX]{x1D6EC}$
. Using Theorem 7.5,
$\hat{R}_{Q}\otimes _{R}\unicode[STIX]{x1D6EC}$
. Using Theorem 7.5,
![]() $K_{P}$
is the canonical (resp. right canonical) module of
$K_{P}$
is the canonical (resp. right canonical) module of
![]() $\unicode[STIX]{x1D6EC}_{P}$
. The last assertion follows.◻
$\unicode[STIX]{x1D6EC}_{P}$
. The last assertion follows.◻
7.7
Let
![]() $(R,\mathfrak{m})$
be local, and assume that
$(R,\mathfrak{m})$
be local, and assume that
![]() $K_{\unicode[STIX]{x1D6EC}}$
exists. Assume that
$K_{\unicode[STIX]{x1D6EC}}$
exists. Assume that
![]() $\unicode[STIX]{x1D6EC}$
is a faithful
$\unicode[STIX]{x1D6EC}$
is a faithful
![]() $R$
-module. Then it is a
$R$
-module. Then it is a
![]() $2$
-canonical
$2$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
by Corollary 7.6. Letting
$R$
by Corollary 7.6. Letting
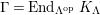 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
,
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
,
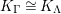 $K_{\unicode[STIX]{x1D6E4}}\cong K_{\unicode[STIX]{x1D6EC}}$
as
$K_{\unicode[STIX]{x1D6E4}}\cong K_{\unicode[STIX]{x1D6EC}}$
as
![]() $\unicode[STIX]{x1D6EC}$
-bimodules by Corollary 6.22. So by Corollary 6.28, there exists some
$\unicode[STIX]{x1D6EC}$
-bimodules by Corollary 6.22. So by Corollary 6.28, there exists some
![]() $\unicode[STIX]{x1D6E4}$
-bimodule structure of
$\unicode[STIX]{x1D6E4}$
-bimodule structure of
![]() $K_{\unicode[STIX]{x1D6EC}}$
such that
$K_{\unicode[STIX]{x1D6EC}}$
such that
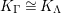 $K_{\unicode[STIX]{x1D6E4}}\cong K_{\unicode[STIX]{x1D6EC}}$
as
$K_{\unicode[STIX]{x1D6E4}}\cong K_{\unicode[STIX]{x1D6EC}}$
as
![]() $\unicode[STIX]{x1D6E4}$
-bimodules. As the left
$\unicode[STIX]{x1D6E4}$
-bimodules. As the left
![]() $\unicode[STIX]{x1D6E4}$
-module structure of
$\unicode[STIX]{x1D6E4}$
-module structure of
![]() $K_{\unicode[STIX]{x1D6EC}}$
which extends the original left
$K_{\unicode[STIX]{x1D6EC}}$
which extends the original left
![]() $\unicode[STIX]{x1D6EC}$
-module structure is unique, and it is the obvious action of
$\unicode[STIX]{x1D6EC}$
-module structure is unique, and it is the obvious action of
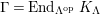 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
. Similarly the right action of
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
. Similarly the right action of
![]() $\unicode[STIX]{x1D6E4}$
is the obvious action of
$\unicode[STIX]{x1D6E4}$
is the obvious action of
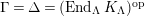 $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}$
; see (6.26).
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}K_{\unicode[STIX]{x1D6EC}})^{op}$
; see (6.26).
8 Evans–Griffith’s theorem for
 $n$
-canonical modules
$n$
-canonical modules
Lemma 8.1. (cf. [Reference AoyamaAoy, Proposition 2], [Reference OgomaOgo, Proposition 4.2], [Reference Aoyama and GotoAoyG, Proposition 1.2])
Let
![]() $(R,\mathfrak{m})$
be local and assume that
$(R,\mathfrak{m})$
be local and assume that
![]() $\unicode[STIX]{x1D6EC}$
has a canonical module
$\unicode[STIX]{x1D6EC}$
has a canonical module
![]() $K_{\unicode[STIX]{x1D6EC}}$
. Then we have
$K_{\unicode[STIX]{x1D6EC}}$
. Then we have
-
(1)
 $\unicode[STIX]{x1D706}_{R}:\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is injective if and only if
$\unicode[STIX]{x1D706}_{R}:\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is injective if and only if
 $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
 $(S_{1}^{\prime })^{R}$
condition and
$(S_{1}^{\prime })^{R}$
condition and
 $Supp_{R}\unicode[STIX]{x1D6EC}$
is equidimensional.
$Supp_{R}\unicode[STIX]{x1D6EC}$
is equidimensional. -
(2)
 $\unicode[STIX]{x1D706}_{R}:\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is bijective if and only if
$\unicode[STIX]{x1D706}_{R}:\unicode[STIX]{x1D6EC}\rightarrow End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is bijective if and only if
 $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
 $(S_{2}^{\prime })^{R}$
condition.
$(S_{2}^{\prime })^{R}$
condition.
Proof. Replacing
![]() $R$
by
$R$
by
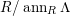 $R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
$R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
![]() $\unicode[STIX]{x1D6EC}$
is a faithful
$\unicode[STIX]{x1D6EC}$
is a faithful
![]() $R$
-module. Then
$R$
-module. Then
![]() $K_{\unicode[STIX]{x1D6EC}}$
is a
$K_{\unicode[STIX]{x1D6EC}}$
is a
![]() $2$
-canonical
$2$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
by Corollary 7.6.
$R$
by Corollary 7.6.
![]() $K_{\unicode[STIX]{x1D6EC}}$
is full if and only if
$K_{\unicode[STIX]{x1D6EC}}$
is full if and only if
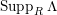 $Supp_{R}\unicode[STIX]{x1D6EC}$
is equidimensional by Lemma 5.10(1).
$Supp_{R}\unicode[STIX]{x1D6EC}$
is equidimensional by Lemma 5.10(1).
Now (1) is a consequence of Lemma 6.19. (2) follows from Corollary 6.25 and Lemma 5.12. ◻
Proposition 8.2. (cf. [Reference Aoyama and GotoAoyG, (2.3)])
Let
![]() $(R,\mathfrak{m})$
be a local ring, and assume that there is an
$(R,\mathfrak{m})$
be a local ring, and assume that there is an
![]() $R$
-canonical module
$R$
-canonical module
![]() $K_{\unicode[STIX]{x1D6EC}}$
of
$K_{\unicode[STIX]{x1D6EC}}$
of
![]() $\unicode[STIX]{x1D6EC}$
. Assume that
$\unicode[STIX]{x1D6EC}$
. Assume that
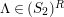 $\unicode[STIX]{x1D6EC}\in (S_{2})^{R}$
, and
$\unicode[STIX]{x1D6EC}\in (S_{2})^{R}$
, and
![]() $K_{\unicode[STIX]{x1D6EC}}$
is a Cohen–Macaulay
$K_{\unicode[STIX]{x1D6EC}}$
is a Cohen–Macaulay
![]() $R$
-module. Then
$R$
-module. Then
![]() $\unicode[STIX]{x1D6EC}$
is Cohen–Macaulay. If, moreover,
$\unicode[STIX]{x1D6EC}$
is Cohen–Macaulay. If, moreover,
![]() $K_{\unicode[STIX]{x1D6EC}}$
is maximal Cohen–Macaulay, then so is
$K_{\unicode[STIX]{x1D6EC}}$
is maximal Cohen–Macaulay, then so is
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Proof. The second assertion follows from the first. We prove the first assertion. Replacing
![]() $R$
by
$R$
by
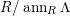 $R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
$R/ann_{R}\unicode[STIX]{x1D6EC}$
, we may assume that
![]() $\unicode[STIX]{x1D6EC}$
is faithful. Let
$\unicode[STIX]{x1D6EC}$
is faithful. Let
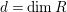 $d=\dim R$
. So
$d=\dim R$
. So
![]() $\unicode[STIX]{x1D6EC}$
satisfies
$\unicode[STIX]{x1D6EC}$
satisfies
![]() $(S_{2}^{\prime })$
, and
$(S_{2}^{\prime })$
, and
![]() $K_{\unicode[STIX]{x1D6EC}}$
is maximal Cohen–Macaulay. As
$K_{\unicode[STIX]{x1D6EC}}$
is maximal Cohen–Macaulay. As
![]() $K_{\unicode[STIX]{x1D6EC}}$
is the lowest nonvanishing cohomology of
$K_{\unicode[STIX]{x1D6EC}}$
is the lowest nonvanishing cohomology of
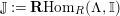 $\mathbb{J}:=\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
, there is a natural map
$\mathbb{J}:=\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I})$
, there is a natural map
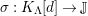 $\unicode[STIX]{x1D70E}:K_{\unicode[STIX]{x1D6EC}}[d]\rightarrow \mathbb{J}$
which induces an isomorphism on the
$\unicode[STIX]{x1D70E}:K_{\unicode[STIX]{x1D6EC}}[d]\rightarrow \mathbb{J}$
which induces an isomorphism on the
![]() $-d$
th cohomology groups. Then the diagram
$-d$
th cohomology groups. Then the diagram

is commutative. The top horizontal arrow
![]() $\unicode[STIX]{x1D706}$
is an isomorphism by Lemma 8.1. Note that
$\unicode[STIX]{x1D706}$
is an isomorphism by Lemma 8.1. Note that
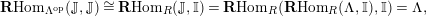 $$\begin{eqnarray}\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(\mathbb{J},\mathbb{J})\cong \mathbf{R}\text{Hom}_{R}(\mathbb{J},\mathbb{I})=\mathbf{R}\text{Hom}_{R}(\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I}),\mathbb{I})=\unicode[STIX]{x1D6EC},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(\mathbb{J},\mathbb{J})\cong \mathbf{R}\text{Hom}_{R}(\mathbb{J},\mathbb{I})=\mathbf{R}\text{Hom}_{R}(\mathbf{R}\text{Hom}_{R}(\unicode[STIX]{x1D6EC},\mathbb{I}),\mathbb{I})=\unicode[STIX]{x1D6EC},\end{eqnarray}$$
and the left vertical arrow is an isomorphism. As
![]() $K_{\unicode[STIX]{x1D6EC}}$
is maximal Cohen–Macaulay,
$K_{\unicode[STIX]{x1D6EC}}$
is maximal Cohen–Macaulay,
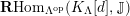 $\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(K_{\unicode[STIX]{x1D6EC}}[d],\mathbb{J})$
is concentrated in degree zero. As
$\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}^{op}}(K_{\unicode[STIX]{x1D6EC}}[d],\mathbb{J})$
is concentrated in degree zero. As
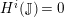 $H^{i}(\mathbb{J})=0$
for
$H^{i}(\mathbb{J})=0$
for
![]() $i<-d$
, we have that the right vertical arrow
$i<-d$
, we have that the right vertical arrow
![]() $\unicode[STIX]{x1D70E}_{\ast }$
is an isomorphism. Thus the bottom horizontal arrow
$\unicode[STIX]{x1D70E}_{\ast }$
is an isomorphism. Thus the bottom horizontal arrow
![]() $\unicode[STIX]{x1D70E}^{\ast }$
is an isomorphism. Applying
$\unicode[STIX]{x1D70E}^{\ast }$
is an isomorphism. Applying
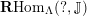 $\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}}(?,\mathbb{J})$
to this map, we have that
$\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6EC}}(?,\mathbb{J})$
to this map, we have that
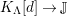 $K_{\unicode[STIX]{x1D6EC}}[d]\rightarrow \mathbb{J}$
is an isomorphism. So
$K_{\unicode[STIX]{x1D6EC}}[d]\rightarrow \mathbb{J}$
is an isomorphism. So
![]() $\unicode[STIX]{x1D6EC}$
is Cohen–Macaulay, as desired.◻
$\unicode[STIX]{x1D6EC}$
is Cohen–Macaulay, as desired.◻
Corollary 8.3. (cf. [Reference Aoyama and GotoAoyG, (2.2)])
Let
![]() $(R,\mathfrak{m})$
be a local ring, and assume that there is an
$(R,\mathfrak{m})$
be a local ring, and assume that there is an
![]() $R$
-canonical module
$R$
-canonical module
![]() $K_{\unicode[STIX]{x1D6EC}}$
of
$K_{\unicode[STIX]{x1D6EC}}$
of
![]() $\unicode[STIX]{x1D6EC}$
. Then
$\unicode[STIX]{x1D6EC}$
. Then
![]() $K_{\unicode[STIX]{x1D6EC}}$
is a Cohen–Macaulay (resp. maximal Cohen–Macaulay)
$K_{\unicode[STIX]{x1D6EC}}$
is a Cohen–Macaulay (resp. maximal Cohen–Macaulay)
![]() $R$
-module if and only if
$R$
-module if and only if
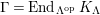 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is so.
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}K_{\unicode[STIX]{x1D6EC}}$
is so.
Proof. As
![]() $K_{\unicode[STIX]{x1D6EC}}$
and
$K_{\unicode[STIX]{x1D6EC}}$
and
![]() $\unicode[STIX]{x1D6E4}$
have the same support, if both of them are Cohen–Macaulay and one of them are maximal Cohen–Macaulay, then the other is also. So it suffices to prove the assertion on the Cohen–Macaulay property. To verify this, we may assume that
$\unicode[STIX]{x1D6E4}$
have the same support, if both of them are Cohen–Macaulay and one of them are maximal Cohen–Macaulay, then the other is also. So it suffices to prove the assertion on the Cohen–Macaulay property. To verify this, we may assume that
![]() $\unicode[STIX]{x1D6EC}$
is a faithful
$\unicode[STIX]{x1D6EC}$
is a faithful
![]() $R$
-module. Note that
$R$
-module. Note that
![]() $\unicode[STIX]{x1D6E4}$
satisfies
$\unicode[STIX]{x1D6E4}$
satisfies
![]() $(S_{2}^{\prime })$
. By Corollary 6.22,
$(S_{2}^{\prime })$
. By Corollary 6.22,
![]() $K_{\unicode[STIX]{x1D6EC}}$
is Cohen–Macaulay if and only if
$K_{\unicode[STIX]{x1D6EC}}$
is Cohen–Macaulay if and only if
![]() $K_{\unicode[STIX]{x1D6E4}}$
is. If
$K_{\unicode[STIX]{x1D6E4}}$
is. If
![]() $\unicode[STIX]{x1D6E4}$
is Cohen–Macaulay, then
$\unicode[STIX]{x1D6E4}$
is Cohen–Macaulay, then
![]() $K_{\unicode[STIX]{x1D6E4}}$
is Cohen–Macaulay by (5.18). Conversely, if
$K_{\unicode[STIX]{x1D6E4}}$
is Cohen–Macaulay by (5.18). Conversely, if
![]() $K_{\unicode[STIX]{x1D6E4}}$
is Cohen–Macaulay, then
$K_{\unicode[STIX]{x1D6E4}}$
is Cohen–Macaulay, then
![]() $\unicode[STIX]{x1D6E4}$
is Cohen–Macaulay by Proposition 8.2.◻
$\unicode[STIX]{x1D6E4}$
is Cohen–Macaulay by Proposition 8.2.◻
Theorem 8.4. (cf. [Reference Evans and GriffithEvG, (3.8)], [Reference Araya and IimaArI, (3.1)])
Let
![]() $R$
be a Noetherian commutative ring, and
$R$
be a Noetherian commutative ring, and
![]() $\unicode[STIX]{x1D6EC}$
a module-finite
$\unicode[STIX]{x1D6EC}$
a module-finite
![]() $R$
-algebra, which need not be commutative. Let
$R$
-algebra, which need not be commutative. Let
![]() $n\geqslant 1$
, and
$n\geqslant 1$
, and
![]() $C$
be a right
$C$
be a right
![]() $n$
-canonical
$n$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-module. Set
$\unicode[STIX]{x1D6EC}$
-module. Set
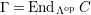 $\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Let
$\unicode[STIX]{x1D6E4}= End_{\unicode[STIX]{x1D6EC}^{op}}C$
. Let
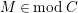 $M\in modC$
. Then the following are equivalent.
$M\in modC$
. Then the following are equivalent.
-
(1)
 $M\in TF(n,C)$
. That is,
$M\in TF(n,C)$
. That is,
 $M$
is
$M$
is
 $(n,C)$
-TF.
$(n,C)$
-TF. -
(2)
 $M\in UP(n,C)$
. That is,
$M\in UP(n,C)$
. That is,
 $M$
has an
$M$
has an
 $(n,C)$
-universal pushforward.
$(n,C)$
-universal pushforward. -
(3)
 $M\in Syz(n,C)$
. That is,
$M\in Syz(n,C)$
. That is,
 $M$
is an
$M$
is an
 $(n,C)$
-syzygy.
$(n,C)$
-syzygy. -
(4)
 $M\in (S_{n}^{\prime })_{C}$
. That is,
$M\in (S_{n}^{\prime })_{C}$
. That is,
 $M$
satisfies the
$M$
satisfies the
 $(S_{n}^{\prime })$
condition as an
$(S_{n}^{\prime })$
condition as an
 $R$
-module, and
$R$
-module, and
 $SuppM\subset SuppC$
.
$SuppM\subset SuppC$
.
Proof. (1)
![]() $\Rightarrow$
(2)
$\Rightarrow$
(2)
![]() $\Rightarrow$
(3)
$\Rightarrow$
(3)
![]() $\Rightarrow$
(4) is easy. We prove (4)
$\Rightarrow$
(4) is easy. We prove (4)
![]() $\Rightarrow$
(1). By Lemma 6.5, we may assume that
$\Rightarrow$
(1). By Lemma 6.5, we may assume that
![]() $n\geqslant 2$
. By Lemma 6.24,
$n\geqslant 2$
. By Lemma 6.24,
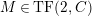 $M\in TF(2,C)$
. Let
$M\in TF(2,C)$
. Let
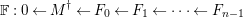 $$\begin{eqnarray}\mathbb{F}:0\leftarrow M^{\dagger }\leftarrow F_{0}\leftarrow F_{1}\leftarrow \cdots \leftarrow F_{n-1}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{F}:0\leftarrow M^{\dagger }\leftarrow F_{0}\leftarrow F_{1}\leftarrow \cdots \leftarrow F_{n-1}\end{eqnarray}$$
be a resolution of
![]() $M^{\dagger }$
in
$M^{\dagger }$
in
![]() $\unicode[STIX]{x1D6E4}{\rm mod}$
with each
$\unicode[STIX]{x1D6E4}{\rm mod}$
with each
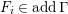 $F_{i}\in add\unicode[STIX]{x1D6E4}$
. It suffices to prove its dual
$F_{i}\in add\unicode[STIX]{x1D6E4}$
. It suffices to prove its dual
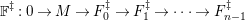 $$\begin{eqnarray}\mathbb{F}^{\ddagger }:0\rightarrow M\rightarrow F_{0}^{\ddagger }\rightarrow F_{1}^{\ddagger }\rightarrow \cdots \rightarrow F_{n-1}^{\ddagger }\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{F}^{\ddagger }:0\rightarrow M\rightarrow F_{0}^{\ddagger }\rightarrow F_{1}^{\ddagger }\rightarrow \cdots \rightarrow F_{n-1}^{\ddagger }\end{eqnarray}$$
is acyclic. By Lemma 2.10, we may localize at
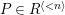 $P\in R^{\langle {<}n\rangle }$
, and may assume that
$P\in R^{\langle {<}n\rangle }$
, and may assume that
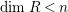 $\dim R<n$
. If
$\dim R<n$
. If
![]() $M=0$
, then
$M=0$
, then
![]() $\mathbb{F}$
is split exact, and so
$\mathbb{F}$
is split exact, and so
![]() $\mathbb{F}^{\ddagger }$
is also exact. So we may assume that
$\mathbb{F}^{\ddagger }$
is also exact. So we may assume that
![]() $M\neq 0$
. Then by assumption,
$M\neq 0$
. Then by assumption,
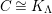 $C\cong K_{\unicode[STIX]{x1D6EC}}$
in
$C\cong K_{\unicode[STIX]{x1D6EC}}$
in
![]() ${\rm mod}\unicode[STIX]{x1D6EC}$
, and
${\rm mod}\unicode[STIX]{x1D6EC}$
, and
![]() $C$
is a maximal Cohen–Macaulay
$C$
is a maximal Cohen–Macaulay
![]() $R$
-module. Hence
$R$
-module. Hence
![]() $\unicode[STIX]{x1D6E4}$
is Cohen–Macaulay by Corollary 8.3. So by (5.16) and Lemma 6.22,
$\unicode[STIX]{x1D6E4}$
is Cohen–Macaulay by Corollary 8.3. So by (5.16) and Lemma 6.22,
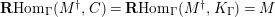 $\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6E4}}(M^{\dagger },C)=\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6E4}}(M^{\dagger },K_{\unicode[STIX]{x1D6E4}})=M$
, and we are done.◻
$\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6E4}}(M^{\dagger },C)=\mathbf{R}\text{Hom}_{\unicode[STIX]{x1D6E4}}(M^{\dagger },K_{\unicode[STIX]{x1D6E4}})=M$
, and we are done.◻
Corollary 8.5. Let the assumptions and notation be as in Theorem 8.4. Let
![]() $n\geqslant 0$
. Assume further that
$n\geqslant 0$
. Assume further that
-
(1)
 $Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(C,C)=0$
for
$Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(C,C)=0$
for
 $1\leqslant i\leqslant n$
;
$1\leqslant i\leqslant n$
; -
(2)
 $C$
is
$C$
is
 $\unicode[STIX]{x1D6EC}$
-full.
$\unicode[STIX]{x1D6EC}$
-full. -
(3)
 $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
 $(S_{n}^{\prime })^{R}$
condition.
$(S_{n}^{\prime })^{R}$
condition.
Then for
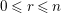 $0\leqslant r\leqslant n$
,
$0\leqslant r\leqslant n$
,
![]() $\text{}^{\bot _{r}}C$
is contravariantly finite in
$\text{}^{\bot _{r}}C$
is contravariantly finite in
![]() ${\rm mod}\unicode[STIX]{x1D6EC}$
.
${\rm mod}\unicode[STIX]{x1D6EC}$
.
Proof. For any
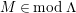 $M\in mod\unicode[STIX]{x1D6EC}$
, the
$M\in mod\unicode[STIX]{x1D6EC}$
, the
![]() $n$
th syzygy module
$n$
th syzygy module
![]() $\unicode[STIX]{x1D6FA}^{n}M$
satisfies the
$\unicode[STIX]{x1D6FA}^{n}M$
satisfies the
![]() $(S_{n}^{\prime })_{C}^{R}$
-condition by (2) and (3). By Theorem 8.4,
$(S_{n}^{\prime })_{C}^{R}$
-condition by (2) and (3). By Theorem 8.4,
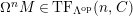 $\unicode[STIX]{x1D6FA}^{n}M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
. By Theorem 3.16,
$\unicode[STIX]{x1D6FA}^{n}M\in TF_{\unicode[STIX]{x1D6EC}^{op}}(n,C)$
. By Theorem 3.16,
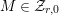 $M\in {\mathcal{Z}}_{r,0}$
, and there is a short exact sequence
$M\in {\mathcal{Z}}_{r,0}$
, and there is a short exact sequence
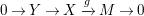 $$\begin{eqnarray}0\rightarrow Y\rightarrow X\xrightarrow[{}]{g}M\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Y\rightarrow X\xrightarrow[{}]{g}M\rightarrow 0\end{eqnarray}$$
with
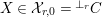 $X\in {\mathcal{X}}_{r,0}=\text{}^{\bot _{r}}C$
and
$X\in {\mathcal{X}}_{r,0}=\text{}^{\bot _{r}}C$
and
![]() $Y\in {\mathcal{Y}}_{r}$
. As
$Y\in {\mathcal{Y}}_{r}$
. As
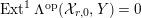 $Ext^{1}\unicode[STIX]{x1D6EC}^{op}({\mathcal{X}}_{r,0},Y)=0$
, we have that
$Ext^{1}\unicode[STIX]{x1D6EC}^{op}({\mathcal{X}}_{r,0},Y)=0$
, we have that
![]() $g$
is a right
$g$
is a right
![]() $\text{}^{\bot _{r}}C$
-approximation, and hence
$\text{}^{\bot _{r}}C$
-approximation, and hence
![]() $\text{}^{\bot _{r}}C$
is contravariantly finite.◻
$\text{}^{\bot _{r}}C$
is contravariantly finite.◻
Corollary 8.6. Let the assumptions and notation be as in Theorem 8.4. Let
![]() $n\geqslant 0$
, and
$n\geqslant 0$
, and
![]() $C$
a
$C$
a
![]() $\unicode[STIX]{x1D6EC}$
-full
$\unicode[STIX]{x1D6EC}$
-full
![]() $(n+2)$
-canonical
$(n+2)$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
. Assume that
$R$
. Assume that
![]() $\unicode[STIX]{x1D6EC}$
satisfies the
$\unicode[STIX]{x1D6EC}$
satisfies the
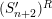 $(S_{n+2}^{\prime })^{R}$
condition. Then
$(S_{n+2}^{\prime })^{R}$
condition. Then
![]() $\text{}^{\bot _{n}}C$
is contravariantly finite in
$\text{}^{\bot _{n}}C$
is contravariantly finite in
![]() ${\rm mod}\unicode[STIX]{x1D6EC}$
.
${\rm mod}\unicode[STIX]{x1D6EC}$
.
Proof. By Corollary 8.5, it suffices to show that
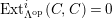 $Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(C,C)=0$
for
$Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(C,C)=0$
for
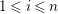 $1\leqslant i\leqslant n$
. Let
$1\leqslant i\leqslant n$
. Let
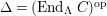 $\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then the canonical map
$\unicode[STIX]{x1D6E5}=(End_{\unicode[STIX]{x1D6EC}}C)^{op}$
. Then the canonical map
![]() $\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E5}$
is an isomorphism by Lemma 6.25, since
$\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6E5}$
is an isomorphism by Lemma 6.25, since
![]() $C$
is a
$C$
is a
![]() $\unicode[STIX]{x1D6EC}$
-full
$\unicode[STIX]{x1D6EC}$
-full
![]() $2$
-canonical
$2$
-canonical
![]() $\unicode[STIX]{x1D6EC}$
-bimodule over
$\unicode[STIX]{x1D6EC}$
-bimodule over
![]() $R$
. As
$R$
. As
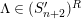 $\unicode[STIX]{x1D6EC}\in (S_{n+2}^{\prime })^{R}$
and
$\unicode[STIX]{x1D6EC}\in (S_{n+2}^{\prime })^{R}$
and
![]() $C$
is a
$C$
is a
![]() $\unicode[STIX]{x1D6EC}$
-full
$\unicode[STIX]{x1D6EC}$
-full
![]() $(n+2)$
-canonical left
$(n+2)$
-canonical left
![]() $\unicode[STIX]{x1D6EC}$
-module over
$\unicode[STIX]{x1D6EC}$
-module over
![]() $R$
, applying Theorem 8.4 to
$R$
, applying Theorem 8.4 to
![]() $\unicode[STIX]{x1D6EC}^{op}$
, we have that
$\unicode[STIX]{x1D6EC}^{op}$
, we have that
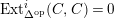 $Ext_{\unicode[STIX]{x1D6E5}^{op}}^{i}(C,C)=0$
for
$Ext_{\unicode[STIX]{x1D6E5}^{op}}^{i}(C,C)=0$
for
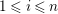 $1\leqslant i\leqslant n$
. As we have
$1\leqslant i\leqslant n$
. As we have
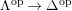 $\unicode[STIX]{x1D6EC}^{op}\rightarrow \unicode[STIX]{x1D6E5}^{op}$
is an isomorphism, we have that
$\unicode[STIX]{x1D6EC}^{op}\rightarrow \unicode[STIX]{x1D6E5}^{op}$
is an isomorphism, we have that
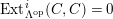 $Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(C,C)=0$
, as desired.◻
$Ext_{\unicode[STIX]{x1D6EC}^{op}}^{i}(C,C)=0$
, as desired.◻
Acknowledgments
Special thanks are due to Professor Osamu Iyama for valuable advice and discussion. Special thanks are also due to Professor Tokuji Araya. This work was motivated by his advice, and Proposition 8.2 is an outcome of discussion with him.
The author is also grateful to Professor Kei-ichiro Iima, Professor Takesi Kawasaki, Professor Shunsuke Takagi, Professor Ryo Takahashi, Professor Kohji Yanagawa, and Professor Yuji Yoshino for valuable advice.