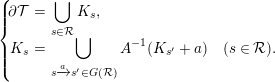1 Introduction
The topology of self-affine tiles has attracted attention from many researchers (see [Reference DekkingDek82a, Reference KenyonKen92, Reference Gröchenig and HaasGH94, Reference Lagarias and WangLW96b, Reference Bandt and GelbrichBG94, Reference Bandt and WangBW01]). This is strongly motivated by the construction of Markov partitions (see [Reference SinaĭSin68, Reference Adler and WeissAW70, Reference BowenBow70, Reference BowenBow78, Reference AdlerAdl98]). After some pioneering works (see [Reference DekkingDek82b, Reference KenyonKen92]), dual tilings of
![]() $\unicode[STIX]{x1D6FD}$
-numeration (see [Reference ThurstonThu89, Reference PraggastisPra92]) and geometric realizations of Pisot substitutions (see [Reference RauzyRau82, Reference Arnoux and ItoAI01]) were systematically studied. The topology of self-affine tiles also shows up in the study of mathematical models of quasicrystals, which initiated a field of research called “mathematics of aperiodic order”, going back to Penrose’s construction (see [Reference KenyonKen96, Reference SolomyakSol97, Reference Baake and MoodyBM04, Reference Kellendonk, Lenz and SavinienKLS15]). It further has connections to theoretical computer science and number theory, and has applications in multiresolution analysis in wavelet expansions (see [Reference Gröchenig and MadychGM92, Reference StrichartzStr93, Reference Gröchenig and HaasGH94, Reference WangWan02, Reference CurryCur06]).
$\unicode[STIX]{x1D6FD}$
-numeration (see [Reference ThurstonThu89, Reference PraggastisPra92]) and geometric realizations of Pisot substitutions (see [Reference RauzyRau82, Reference Arnoux and ItoAI01]) were systematically studied. The topology of self-affine tiles also shows up in the study of mathematical models of quasicrystals, which initiated a field of research called “mathematics of aperiodic order”, going back to Penrose’s construction (see [Reference KenyonKen96, Reference SolomyakSol97, Reference Baake and MoodyBM04, Reference Kellendonk, Lenz and SavinienKLS15]). It further has connections to theoretical computer science and number theory, and has applications in multiresolution analysis in wavelet expansions (see [Reference Gröchenig and MadychGM92, Reference StrichartzStr93, Reference Gröchenig and HaasGH94, Reference WangWan02, Reference CurryCur06]).
We proposed in [Reference Akiyama and LoridantAL11] a standard method to parametrize the boundary of self-affine tiles, aiming at giving broad applications of its fine topological study. So far, several applications to prove or disprove the homeomorphy to the closed disk of several classes of tiles have been performed in [Reference Akiyama and LoridantAL10] and [Reference LoridantLor16]. Boundary parametrization also gives a way to approximate the boundary by a special substitution. Although such studies have already appeared in many articles, we stress that our method is a systematic approach to these questions. In this article, we wish to continue this program. We would like to present a new application of our parametrization in order to obtain information on the interior components of non-disklike tiles.
The topology of non-disklike tiles can be very intricate. We can find several, but not many, papers treating this case. Necessary conditions for the disklikeness of the interior components of self-affine tiles with disconnected interior were given in [Reference Ngai and TangNT04, Reference Ngai and TangNT05]. In [Reference Loridant and ThuswaldnerLT08, Reference Bernat, Loridant and ThuswaldnerBLT10], the interior components of the fundamental domain associated with the complex base
![]() $-2+i$
were described in terms of attractors of graph-directed self-similar sets. In [Reference Ngai and NguyenNN03], the cut points of the Heighway dragon were computed and its interior components were shown to be disklike. Moreover, the finitely many shapes of the interior components of the Levy dragon were studied in [Reference Bailey, Kim and StrichartzBKS02, Reference AlsterAls10].
$-2+i$
were described in terms of attractors of graph-directed self-similar sets. In [Reference Ngai and NguyenNN03], the cut points of the Heighway dragon were computed and its interior components were shown to be disklike. Moreover, the finitely many shapes of the interior components of the Levy dragon were studied in [Reference Bailey, Kim and StrichartzBKS02, Reference AlsterAls10].
Our idea is to have a close look at the set of identifications appearing in our parametrization. In this paper, we introduce a mild class of identifications which satisfies a noncrossing condition. Under this condition and from the computation of the winding number of a given point, we can define an outer identification. This identification is of special importance, because it produces an interior component by taking a pair of such identifications. Then, from the graph of identifications, we can read the distribution of interior components. The boundary of these is a Jordan closed curve given as explicit continuous images of an interval. An important point is that all of the introduced concepts are checkable by algorithm. Finally, we examine our theory by examples. Basically, we may reproduce similar results to those in [Reference Ngai and NguyenNN03] by our method. As it takes many computations for each example, we illustrate our result by giving a concrete computation of a fractal tile due to Bandt and Gelbrich. We can identify the set of cut points and pick an interior component as the interior of a concrete Jordan closed curve (see Theorem 7). We end this paper by giving some examples where the noncrossing condition is violated.
2 Fundamental facts on the boundary parametrization
We recall some fundamental facts on our parametrization method for the boundary of self-affine tiles developed in [Reference Akiyama and LoridantAL11]. Let
![]() $A$
be an expanding real
$A$
be an expanding real
![]() $d\times d$
matrix; that is, the eigenvalues of
$d\times d$
matrix; that is, the eigenvalues of
![]() $A$
are greater than
$A$
are greater than
![]() $1$
in modulus, and
$1$
in modulus, and
![]() ${\mathcal{D}}\subset \mathbb{R}^{d}$
a finite set. Then, there is a unique nonempty compact self-affine set
${\mathcal{D}}\subset \mathbb{R}^{d}$
a finite set. Then, there is a unique nonempty compact self-affine set
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
satisfying
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
satisfying
(see [Reference HutchinsonHut81]).
![]() ${\mathcal{T}}$
is called a self-affine tile if it is equal to the closure of its interior. It satisfies the tiling property if there is a tiling set
${\mathcal{T}}$
is called a self-affine tile if it is equal to the closure of its interior. It satisfies the tiling property if there is a tiling set
![]() ${\mathcal{J}}\subset \mathbb{R}^{d}$
such that
${\mathcal{J}}\subset \mathbb{R}^{d}$
such that
Fundamental properties of self-affine tiles were studied in [Reference Gröchenig and HaasGH94, Reference Lagarias and WangLW96a, Reference Lagarias and WangLW96b]. If
![]() $A$
has integer coefficients and
$A$
has integer coefficients and
![]() ${\mathcal{D}}\subset \mathbb{Z}^{d}$
is a complete residue system of
${\mathcal{D}}\subset \mathbb{Z}^{d}$
is a complete residue system of
![]() $\mathbb{Z}^{d}$
modulo
$\mathbb{Z}^{d}$
modulo
![]() $A\mathbb{Z}^{d}$
, then
$A\mathbb{Z}^{d}$
, then
![]() ${\mathcal{T}}$
satisfies the tiling property for some sublattice
${\mathcal{T}}$
satisfies the tiling property for some sublattice
![]() ${\mathcal{J}}$
of
${\mathcal{J}}$
of
![]() $\mathbb{Z}^{d}$
[Reference Lagarias and WangLW97]. Conditions under which
$\mathbb{Z}^{d}$
[Reference Lagarias and WangLW97]. Conditions under which
![]() ${\mathcal{J}}=\mathbb{Z}^{d}$
are investigated in [Reference Gröchenig and HaasGH94, Reference VinceVin00]. We then say that
${\mathcal{J}}=\mathbb{Z}^{d}$
are investigated in [Reference Gröchenig and HaasGH94, Reference VinceVin00]. We then say that
![]() ${\mathcal{T}}$
is an integral self-affine
${\mathcal{T}}$
is an integral self-affine
![]() $\mathbb{Z}^{d}$
-tile.
$\mathbb{Z}^{d}$
-tile.
A powerful tool in the study of an integral self-affine
![]() $\mathbb{Z}^{d}$
-tile
$\mathbb{Z}^{d}$
-tile
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
is the boundary automaton. For a set
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
is the boundary automaton. For a set
![]() $U\subset \mathbb{Z}^{d}$
, we define the following automaton
$U\subset \mathbb{Z}^{d}$
, we define the following automaton
![]() $G(U)$
.
$G(U)$
.
-
∙ The set of vertices is
 $U$
.
$U$
. -
∙ There is an edge
 $s\xrightarrow[{}]{a|a^{\prime }}s^{\prime }$
(
$s\xrightarrow[{}]{a|a^{\prime }}s^{\prime }$
(
 $s,s^{\prime }\in U,a,a^{\prime }\in {\mathcal{D}}$
) if and only if
$s,s^{\prime }\in U,a,a^{\prime }\in {\mathcal{D}}$
) if and only if
 $As+a^{\prime }=s+a$
. We may simply write
$As+a^{\prime }=s+a$
. We may simply write
 $s\xrightarrow[{}]{a}s^{\prime }\in G(U)$
. (This determines
$s\xrightarrow[{}]{a}s^{\prime }\in G(U)$
. (This determines
 $a^{\prime }$
uniquely.)
$a^{\prime }$
uniquely.)
Taking for
![]() $U$
the set
$U$
the set
we obtain the boundary automaton
![]() $G({\mathcal{S}})$
. By compactness of
$G({\mathcal{S}})$
. By compactness of
![]() ${\mathcal{T}}$
,
${\mathcal{T}}$
,
![]() ${\mathcal{S}}$
is finite. There exist algorithms to compute
${\mathcal{S}}$
is finite. There exist algorithms to compute
![]() $G({\mathcal{S}})$
from the data
$G({\mathcal{S}})$
from the data
![]() $(A,{\mathcal{D}})$
(see, for example, [Reference Scheicher and ThuswaldnerST03]). This automaton gives a way to express the boundary as the attractor of a graph-directed iterated function system (GIFS) (see [Reference Mauldin and WilliamsMW88]).
$(A,{\mathcal{D}})$
(see, for example, [Reference Scheicher and ThuswaldnerST03]). This automaton gives a way to express the boundary as the attractor of a graph-directed iterated function system (GIFS) (see [Reference Mauldin and WilliamsMW88]).
Proposition 2.1. Given an integral self-affine
![]() $\mathbb{Z}^{d}$
-tile
$\mathbb{Z}^{d}$
-tile
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
and its boundary automaton
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
and its boundary automaton
![]() $G({\mathcal{S}})$
, the boundary
$G({\mathcal{S}})$
, the boundary
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
satisfies
$\unicode[STIX]{x2202}{\mathcal{T}}$
satisfies
where for all
![]() $s\in {\mathcal{S}}$
,
$s\in {\mathcal{S}}$
,
Moreover,
![]() $B_{s}={\mathcal{T}}\cap ({\mathcal{T}}+s)$
, and for two sequences of digits
$B_{s}={\mathcal{T}}\cap ({\mathcal{T}}+s)$
, and for two sequences of digits
![]() $(a_{i})_{i\geqslant 1}$
,
$(a_{i})_{i\geqslant 1}$
,
![]() $(a_{i}^{\prime })$
, we have
$(a_{i}^{\prime })$
, we have
if and only if there is an infinite walk
Usually, the boundary automaton contains a great deal of redundant information, due to the existence of multiple points in the tiling. This often makes
![]() $G({\mathcal{S}})$
too large to perform our parametrization method. We make the following assumptions.
$G({\mathcal{S}})$
too large to perform our parametrization method. We make the following assumptions.
Assumption 1. There exists a set
![]() ${\mathcal{R}}\subset {\mathcal{S}}$
such that the following holds.
${\mathcal{R}}\subset {\mathcal{S}}$
such that the following holds.
-
∙
 $G({\mathcal{R}})$
is strongly connected; that is, its incidence matrix is irreducible.
$G({\mathcal{R}})$
is strongly connected; that is, its incidence matrix is irreducible. $$\begin{eqnarray}\mathbf{C}=(c_{s,s^{\prime }})_{s,s^{\prime }\in {\mathcal{R}}}\quad \text{with }c_{s,s^{\prime }}=\#\{s^{\prime }\xrightarrow[{}]{}s\in G({\mathcal{R}})\}\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{C}=(c_{s,s^{\prime }})_{s,s^{\prime }\in {\mathcal{R}}}\quad \text{with }c_{s,s^{\prime }}=\#\{s^{\prime }\xrightarrow[{}]{}s\in G({\mathcal{R}})\}\end{eqnarray}$$
-
∙
 $G({\mathcal{R}})$
is a GIFS for
$G({\mathcal{R}})$
is a GIFS for
 $\unicode[STIX]{x2202}{\mathcal{T}}$
; that is, (2.1)In this case,
$\unicode[STIX]{x2202}{\mathcal{T}}$
; that is, (2.1)In this case, $$\begin{eqnarray}\left\{\!\begin{array}{@{}rcl@{}}\unicode[STIX]{x2202}{\mathcal{T}}\ & =\ & \displaystyle \mathop{\bigcup }_{s\in {\mathcal{R}}}K_{s},\\ K_{s}\ & =\ & \displaystyle \mathop{\bigcup }_{s\xrightarrow[{}]{a}s^{\prime }\in G({\mathcal{R}})}A^{-1}(K_{s^{\prime }}+a)\quad (s\in {\mathcal{R}}).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\!\begin{array}{@{}rcl@{}}\unicode[STIX]{x2202}{\mathcal{T}}\ & =\ & \displaystyle \mathop{\bigcup }_{s\in {\mathcal{R}}}K_{s},\\ K_{s}\ & =\ & \displaystyle \mathop{\bigcup }_{s\xrightarrow[{}]{a}s^{\prime }\in G({\mathcal{R}})}A^{-1}(K_{s^{\prime }}+a)\quad (s\in {\mathcal{R}}).\end{array}\right.\end{eqnarray}$$
 $K_{s}\subset {\mathcal{T}}\cap ({\mathcal{T}}+s)$
.
$K_{s}\subset {\mathcal{T}}\cap ({\mathcal{T}}+s)$
.
Remark 2.2. In many applications, a subset of the contact set constructed in [Reference Gröchenig and HaasGH94]) can be used as a good candidate for such a smaller set
![]() ${\mathcal{R}}\subset {\mathcal{S}}$
and leads to the contact automaton. If
${\mathcal{R}}\subset {\mathcal{S}}$
and leads to the contact automaton. If
![]() $A$
is a similarity matrix of factor
$A$
is a similarity matrix of factor
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D6FD}$
is the largest root of the incidence matrix of the contact automaton, it is well known (see [Reference Duvall, Keesling and VinceDKV00]) that the Hausdorff dimension of
$\unicode[STIX]{x1D6FD}$
is the largest root of the incidence matrix of the contact automaton, it is well known (see [Reference Duvall, Keesling and VinceDKV00]) that the Hausdorff dimension of
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
is given by the formula
$\unicode[STIX]{x2202}{\mathcal{T}}$
is given by the formula
As
![]() $G({\mathcal{R}})$
is strongly connected, there is a strictly positive left eigenvector
$G({\mathcal{R}})$
is strongly connected, there is a strictly positive left eigenvector
![]() $(u_{s})_{s\in {\mathcal{R}}}$
of length
$(u_{s})_{s\in {\mathcal{R}}}$
of length
![]() $1$
associated to the Perron–Frobenius eigenvalue
$1$
associated to the Perron–Frobenius eigenvalue
![]() $\unicode[STIX]{x1D6FD}$
of its incidence matrix. The parametrization
$\unicode[STIX]{x1D6FD}$
of its incidence matrix. The parametrization
![]() $C:[0,1]\rightarrow \unicode[STIX]{x2202}{\mathcal{T}}$
is obtained by subdividing the interval
$C:[0,1]\rightarrow \unicode[STIX]{x2202}{\mathcal{T}}$
is obtained by subdividing the interval
![]() $[0,1]$
proportionally to the automaton
$[0,1]$
proportionally to the automaton
![]() $G({\mathcal{R}})$
. In particular, a subinterval of length
$G({\mathcal{R}})$
. In particular, a subinterval of length
![]() $u_{s}$
is mapped to
$u_{s}$
is mapped to
![]() $K_{s}$
for each
$K_{s}$
for each
![]() $s\in {\mathcal{R}}$
. To this effect, we order the boundary pieces
$s\in {\mathcal{R}}$
. To this effect, we order the boundary pieces
![]() $K_{s}$
around the boundary, as well as the subpieces
$K_{s}$
around the boundary, as well as the subpieces
![]() $A^{-1}(K_{s^{\prime }}+a)$
constituting
$A^{-1}(K_{s^{\prime }}+a)$
constituting
![]() $K_{s}$
.
$K_{s}$
.
Under the above Assumption 1, let
![]() $p=|{\mathcal{R}}|$
, and let
$p=|{\mathcal{R}}|$
, and let
![]() ${\mathcal{R}}=:\{s^{1},\ldots ,s^{p}\}$
. This orders the states of
${\mathcal{R}}=:\{s^{1},\ldots ,s^{p}\}$
. This orders the states of
![]() $G({\mathcal{R}})$
arbitrarily from
$G({\mathcal{R}})$
arbitrarily from
![]() $1$
to
$1$
to
![]() $p$
. Similarly, for each
$p$
. Similarly, for each
![]() $i\in \{1,\ldots ,p\}$
, we order all of the edges starting from
$i\in \{1,\ldots ,p\}$
, we order all of the edges starting from
![]() $s^{i}$
arbitrarily, from
$s^{i}$
arbitrarily, from
![]() $\mathbf{1}$
to
$\mathbf{1}$
to
![]() $\mathbf{o}_{\mathbf{m}}$
. Here,
$\mathbf{o}_{\mathbf{m}}$
. Here,
![]() $\mathbf{o}_{\mathbf{m}}$
is the total number of edges starting from
$\mathbf{o}_{\mathbf{m}}$
is the total number of edges starting from
![]() $s^{i}$
, without reference to
$s^{i}$
, without reference to
![]() $i$
for the sake of simplicity. We call the resulting automaton an ordered extension of
$i$
for the sake of simplicity. We call the resulting automaton an ordered extension of
![]() $G({\mathcal{R}})$
and write it as
$G({\mathcal{R}})$
and write it as
![]() $G({\mathcal{R}})^{o}$
. In other words, the mapping
$G({\mathcal{R}})^{o}$
. In other words, the mapping
is a bijection. We can extend this mapping to the walks of arbitrary length in
![]() $G({\mathcal{R}})$
(possibly infinite walks),
$G({\mathcal{R}})$
(possibly infinite walks),
whenever
![]() $i\xrightarrow[{}]{a_{1}|a_{1}^{\prime }||\mathbf{o}_{\mathbf{1}}}j_{1}\xrightarrow[{}]{a_{2}|a_{2}^{\prime }||\mathbf{o}_{\mathbf{2}}}j_{2}\ldots \in G({\mathcal{R}})^{o}$
. Finally, we define the natural onto mapping,
$i\xrightarrow[{}]{a_{1}|a_{1}^{\prime }||\mathbf{o}_{\mathbf{1}}}j_{1}\xrightarrow[{}]{a_{2}|a_{2}^{\prime }||\mathbf{o}_{\mathbf{2}}}j_{2}\ldots \in G({\mathcal{R}})^{o}$
. Finally, we define the natural onto mapping,
whenever
![]() $v:s\xrightarrow[{}]{a_{1}|a_{1}^{\prime }||\mathbf{o}_{\mathbf{1}}}s_{1}\xrightarrow[{}]{a_{2}|a_{2}^{\prime }||\mathbf{o}_{\mathbf{2}}}s_{2}\ldots$
is an infinite walk in
$v:s\xrightarrow[{}]{a_{1}|a_{1}^{\prime }||\mathbf{o}_{\mathbf{1}}}s_{1}\xrightarrow[{}]{a_{2}|a_{2}^{\prime }||\mathbf{o}_{\mathbf{2}}}s_{2}\ldots$
is an infinite walk in
![]() $G({\mathcal{R}})^{o}$
. The automaton
$G({\mathcal{R}})^{o}$
. The automaton
![]() $G({\mathcal{R}})^{o}$
induces a
$G({\mathcal{R}})^{o}$
induces a
![]() $\unicode[STIX]{x1D6FD}$
-number system
$\unicode[STIX]{x1D6FD}$
-number system
![]() $\unicode[STIX]{x1D719}^{(1)}:[0,1]\rightarrow G({\mathcal{R}})^{o}$
of Dumont–Thomas type [Reference Dumont and ThomasDT89]. The following compatibility conditions ensure the continuity of the parametrization.
$\unicode[STIX]{x1D719}^{(1)}:[0,1]\rightarrow G({\mathcal{R}})^{o}$
of Dumont–Thomas type [Reference Dumont and ThomasDT89]. The following compatibility conditions ensure the continuity of the parametrization.
Definition 2.3. (Compatibility conditions)
We call
![]() $G({\mathcal{R}})^{o}$
a compatible ordered extension of
$G({\mathcal{R}})^{o}$
a compatible ordered extension of
![]() $G({\mathcal{R}})$
if
$G({\mathcal{R}})$
if
We denote by
![]() $\overline{\mathbf{o}}$
the infinite repetition of
$\overline{\mathbf{o}}$
the infinite repetition of
![]() $\mathbf{o},\mathbf{o},\ldots .$
Whether an ordered extension is compatible or not can be checked algorithmically. In [Reference Akiyama and LoridantAL11], we proved the following result by taking
$\mathbf{o},\mathbf{o},\ldots .$
Whether an ordered extension is compatible or not can be checked algorithmically. In [Reference Akiyama and LoridantAL11], we proved the following result by taking
![]() $C:=\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D719}^{(1)}$
.
$C:=\unicode[STIX]{x1D6F9}\circ \unicode[STIX]{x1D719}^{(1)}$
.
Theorem 2.4. [Reference Akiyama and LoridantAL11, Theorem 1]
Let
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
be an integral self-affine
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
be an integral self-affine
![]() $\mathbb{Z}^{d}$
-tile, and let the set
$\mathbb{Z}^{d}$
-tile, and let the set
![]() ${\mathcal{R}}$
satisfy the above assumptions. Let
${\mathcal{R}}$
satisfy the above assumptions. Let
![]() $\unicode[STIX]{x1D6FD}$
be the Perron–Frobenius eigenvalue of the incidence matrix of
$\unicode[STIX]{x1D6FD}$
be the Perron–Frobenius eigenvalue of the incidence matrix of
![]() $G({\mathcal{R}})$
. Moreover, suppose that there exists a compatible ordered extension of
$G({\mathcal{R}})$
. Moreover, suppose that there exists a compatible ordered extension of
![]() $G({\mathcal{R}})$
. Then, there exist a Hölder continuous onto mapping
$G({\mathcal{R}})$
. Then, there exist a Hölder continuous onto mapping
![]() $C:[0,1]\rightarrow \unicode[STIX]{x2202}T$
with
$C:[0,1]\rightarrow \unicode[STIX]{x2202}T$
with
![]() $C(0)=C(1)$
and a sequence
$C(0)=C(1)$
and a sequence
![]() $(\unicode[STIX]{x1D6E5}_{n})_{n\geqslant 0}$
of polygonal curves with the following properties.
$(\unicode[STIX]{x1D6E5}_{n})_{n\geqslant 0}$
of polygonal curves with the following properties.
-
(1)
 $\lim _{n\rightarrow \infty }\unicode[STIX]{x1D6E5}_{n}=\unicode[STIX]{x2202}T$
(Hausdorff metric).
$\lim _{n\rightarrow \infty }\unicode[STIX]{x1D6E5}_{n}=\unicode[STIX]{x2202}T$
(Hausdorff metric). -
(2) Denote by
 $V_{n}$
the set of vertices of
$V_{n}$
the set of vertices of
 $\unicode[STIX]{x1D6E5}_{n}$
. For all
$\unicode[STIX]{x1D6E5}_{n}$
. For all
 $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
 $V_{n}\subset V_{n+1}\subset C(\mathbb{Q}(\unicode[STIX]{x1D6FD})\cap [0,1])$
(i.e., the vertices have
$V_{n}\subset V_{n+1}\subset C(\mathbb{Q}(\unicode[STIX]{x1D6FD})\cap [0,1])$
(i.e., the vertices have
 $\mathbb{Q}(\unicode[STIX]{x1D6FD})$
-addresses in the parametrization).
$\mathbb{Q}(\unicode[STIX]{x1D6FD})$
-addresses in the parametrization).
Remark 2.5. The polygonal approximations
![]() $\unicode[STIX]{x1D6E5}_{n}$
appear in a natural way together with the parametrization.
$\unicode[STIX]{x1D6E5}_{n}$
appear in a natural way together with the parametrization.
![]() $\unicode[STIX]{x1D6E5}_{0}$
is obtained by joining by straight line segments the points
$\unicode[STIX]{x1D6E5}_{0}$
is obtained by joining by straight line segments the points
in this order. In general, let
![]() $w_{1}^{(n)},\ldots ,w_{m_{n}}^{(n)}$
be the walks of length
$w_{1}^{(n)},\ldots ,w_{m_{n}}^{(n)}$
be the walks of length
![]() $n$
in the automaton
$n$
in the automaton
![]() $G({\mathcal{R}})^{o}$
, written in the lexicographical order, from
$G({\mathcal{R}})^{o}$
, written in the lexicographical order, from
![]() $(1;\underbrace{\mathbf{1},\ldots ,\mathbf{1}}_{n\,\text{times}})$
to
$(1;\underbrace{\mathbf{1},\ldots ,\mathbf{1}}_{n\,\text{times}})$
to
![]() $(p;\underbrace{\mathbf{o}_{\mathbf{m}},\ldots ,\mathbf{o}_{\mathbf{m}}}_{n\,\text{times}})$
. Let us denote by
$(p;\underbrace{\mathbf{o}_{\mathbf{m}},\ldots ,\mathbf{o}_{\mathbf{m}}}_{n\,\text{times}})$
. Let us denote by
![]() $(i;\mathbf{o}_{\mathbf{1}},\ldots ,\mathbf{o}_{\mathbf{n}})\& \overline{\mathbf{1}}$
the concatenated walk
$(i;\mathbf{o}_{\mathbf{1}},\ldots ,\mathbf{o}_{\mathbf{n}})\& \overline{\mathbf{1}}$
the concatenated walk
![]() $(i;\mathbf{o}_{\mathbf{1}},\ldots ,\mathbf{o}_{\mathbf{n}},\overline{\mathbf{1}})$
. Then,
$(i;\mathbf{o}_{\mathbf{1}},\ldots ,\mathbf{o}_{\mathbf{n}},\overline{\mathbf{1}})$
. Then,
![]() $\unicode[STIX]{x1D6E5}_{n}$
is obtained by joining by straight line segments the points
$\unicode[STIX]{x1D6E5}_{n}$
is obtained by joining by straight line segments the points
in this order. Each vertex of
![]() $\unicode[STIX]{x1D6E5}_{n}$
corresponds to an infinite walk ending up in a cycle of
$\unicode[STIX]{x1D6E5}_{n}$
corresponds to an infinite walk ending up in a cycle of
![]() $G({\mathcal{R}})$
. Thus, these are images of fixed points of contractions,
$G({\mathcal{R}})$
. Thus, these are images of fixed points of contractions,
where
![]() $f_{a}(x):=A^{-1}(x+a)$
for each
$f_{a}(x):=A^{-1}(x+a)$
for each
![]() $a\in {\mathcal{D}}$
.
$a\in {\mathcal{D}}$
.
3 Winding number
The winding number is defined for a simple closed curve
![]() $J$
and a point
$J$
and a point
![]() $x_{0}\not \in J$
in [Reference AlexandrovAle98, Part 1, Chapter II] to show Jordan’s curve theorem.
$x_{0}\not \in J$
in [Reference AlexandrovAle98, Part 1, Chapter II] to show Jordan’s curve theorem.
Assumption 2. We suppose that in each step of the approximation, our standard parametrization gives a simple closed polygonal curve
![]() $\unicode[STIX]{x1D6E5}_{n}$
.
$\unicode[STIX]{x1D6E5}_{n}$
.
This was shown to be the case for many examples, as in [Reference Akiyama and LoridantAL11] or at the end of this article. Then, we can employ the same definition
for the winding number of
![]() $x_{0}$
around
$x_{0}$
around
![]() $J=\unicode[STIX]{x2202}{\mathcal{T}}$
, where the right-hand side is the limit as the broken lines
$J=\unicode[STIX]{x2202}{\mathcal{T}}$
, where the right-hand side is the limit as the broken lines
![]() $\unicode[STIX]{x1D6E5}_{n}$
converge to the boundary in the Hausdorff metric. Since
$\unicode[STIX]{x1D6E5}_{n}$
converge to the boundary in the Hausdorff metric. Since
![]() $\{x_{0}\}$
and
$\{x_{0}\}$
and
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
are closed sets, they are separated by a positive distance if
$\unicode[STIX]{x2202}{\mathcal{T}}$
are closed sets, they are separated by a positive distance if
![]() $x_{0}\not \in \unicode[STIX]{x2202}{\mathcal{T}}$
. Therefore, if the approximation of
$x_{0}\not \in \unicode[STIX]{x2202}{\mathcal{T}}$
. Therefore, if the approximation of
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
by broken lines is fine enough, then
$\unicode[STIX]{x2202}{\mathcal{T}}$
by broken lines is fine enough, then
![]() $W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
is computed as a finite sum and the above
$W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
is computed as a finite sum and the above
![]() $W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
is well-defined. Clearly,
$W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
is well-defined. Clearly,
![]() $W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})=1$
(resp. 0) if
$W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})=1$
(resp. 0) if
![]() $x_{0}$
is an inner point of
$x_{0}$
is an inner point of
![]() ${\mathcal{T}}$
(resp. outside of
${\mathcal{T}}$
(resp. outside of
![]() ${\mathcal{T}}$
).
${\mathcal{T}}$
).
Using the encircling method introduced by Akiyama and Sadahiro in [Reference Akiyama and SadahiroAS98], we can give a covering of
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
by a finite number of disks whose union does not contain
$\unicode[STIX]{x2202}{\mathcal{T}}$
by a finite number of disks whose union does not contain
![]() $x_{0}$
. By this method, we can deduce how many steps of approximation by broken lines are necessary to compute the winding number
$x_{0}$
. By this method, we can deduce how many steps of approximation by broken lines are necessary to compute the winding number
![]() $W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
when
$W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
when
![]() $x_{0}\not \in \unicode[STIX]{x2202}{\mathcal{T}}$
. This gives an easy application of the boundary parametrization, described by the following theorem. Given a self-affine tile
$x_{0}\not \in \unicode[STIX]{x2202}{\mathcal{T}}$
. This gives an easy application of the boundary parametrization, described by the following theorem. Given a self-affine tile
![]() ${\mathcal{T}}$
satisfying Assumptions 1 and 2, and
${\mathcal{T}}$
satisfying Assumptions 1 and 2, and
![]() $x_{0}\in \unicode[STIX]{x2202}{\mathcal{T}}$
, a computer calculation can decide whether
$x_{0}\in \unicode[STIX]{x2202}{\mathcal{T}}$
, a computer calculation can decide whether
![]() $x_{0}$
is an inner point of
$x_{0}$
is an inner point of
![]() ${\mathcal{T}}$
or of
${\mathcal{T}}$
or of
![]() $\mathbb{R}^{2}\setminus {\mathcal{T}}$
.
$\mathbb{R}^{2}\setminus {\mathcal{T}}$
.
Theorem 1. For a given point
![]() $x_{0}\not \in \unicode[STIX]{x2202}T$
, there is an algorithm to tell whether
$x_{0}\not \in \unicode[STIX]{x2202}T$
, there is an algorithm to tell whether
![]() $x_{0}$
is an inner point of
$x_{0}$
is an inner point of
![]() ${\mathcal{T}}$
or of
${\mathcal{T}}$
or of
![]() $\mathbb{R}^{2}\setminus {\mathcal{T}}$
.
$\mathbb{R}^{2}\setminus {\mathcal{T}}$
.
Proof. Since
![]() $A$
is an expanding matrix, we can find
$A$
is an expanding matrix, we can find
![]() $k>0$
and
$k>0$
and
![]() $0<\unicode[STIX]{x1D706}<1$
such that
$0<\unicode[STIX]{x1D706}<1$
such that
![]() $A^{-k}\mathbb{D}(0;1)\subset \unicode[STIX]{x1D706}\mathbb{D}(0;1)$
. Here,
$A^{-k}\mathbb{D}(0;1)\subset \unicode[STIX]{x1D706}\mathbb{D}(0;1)$
. Here,
![]() $\mathbb{D}(0;1)$
denotes the closed disk of center
$\mathbb{D}(0;1)$
denotes the closed disk of center
![]() $0$
and radius
$0$
and radius
![]() $1$
. For the sake of simplicity, we write the proof under the assumption that
$1$
. For the sake of simplicity, we write the proof under the assumption that
![]() $k=1$
. If
$k=1$
. If
![]() $k>1$
, the argument below remains true by taking
$k>1$
, the argument below remains true by taking
![]() $A^{\prime }:=A^{k}$
and
$A^{\prime }:=A^{k}$
and
![]() ${\mathcal{D}}^{\prime }={\mathcal{D}}+A{\mathcal{D}}+\cdots +A^{k-1}{\mathcal{D}}$
. Note that the associated tile
${\mathcal{D}}^{\prime }={\mathcal{D}}+A{\mathcal{D}}+\cdots +A^{k-1}{\mathcal{D}}$
. Note that the associated tile
![]() ${\mathcal{T}}^{\prime }$
satisfies
${\mathcal{T}}^{\prime }$
satisfies
![]() ${\mathcal{T}}^{\prime }={\mathcal{T}}$
.
${\mathcal{T}}^{\prime }={\mathcal{T}}$
.
Since
![]() ${\mathcal{T}}$
is compact, there is
${\mathcal{T}}$
is compact, there is
![]() $r>0$
such that
$r>0$
such that
![]() ${\mathcal{T}}\subset \mathbb{D}(0;r)=:\mathbb{D}_{r}$
. In particular, for all
${\mathcal{T}}\subset \mathbb{D}(0;r)=:\mathbb{D}_{r}$
. In particular, for all
![]() $m\geqslant 0$
,
$m\geqslant 0$
,
the latter set being a closed disk of diameter
![]() $2r\unicode[STIX]{x1D706}^{m}$
. We show that
$2r\unicode[STIX]{x1D706}^{m}$
. We show that
![]() $W(x_{0},\unicode[STIX]{x1D6E5}_{m})=W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
as soon as
$W(x_{0},\unicode[STIX]{x1D6E5}_{m})=W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
as soon as
![]() $m$
satisfies
$m$
satisfies
Indeed, iterating (2.1), for all
![]() $m\geqslant 1$
, we can write
$m\geqslant 1$
, we can write
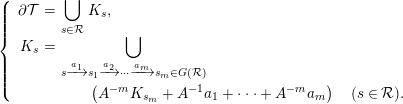 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}rcl@{}}\unicode[STIX]{x2202}{\mathcal{T}}\ & =\ & \displaystyle \mathop{\bigcup }_{s\in {\mathcal{R}}}K_{s},\\ K_{s}\ & =\ & \displaystyle \mathop{\bigcup }_{s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{m}}s_{m}\in G({\mathcal{R}})}\\ \ & \ & \qquad \left(A^{-m}K_{s_{m}}+A^{-1}a_{1}+\cdots +A^{-m}a_{m}\right)\quad (s\in {\mathcal{R}}).\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}rcl@{}}\unicode[STIX]{x2202}{\mathcal{T}}\ & =\ & \displaystyle \mathop{\bigcup }_{s\in {\mathcal{R}}}K_{s},\\ K_{s}\ & =\ & \displaystyle \mathop{\bigcup }_{s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{m}}s_{m}\in G({\mathcal{R}})}\\ \ & \ & \qquad \left(A^{-m}K_{s_{m}}+A^{-1}a_{1}+\cdots +A^{-m}a_{m}\right)\quad (s\in {\mathcal{R}}).\end{array}\right. & & \displaystyle\end{eqnarray}$$
Using that
![]() $K_{s}\subset {\mathcal{T}}\subset \mathbb{D}_{r}$
for all
$K_{s}\subset {\mathcal{T}}\subset \mathbb{D}_{r}$
for all
![]() $s\in {\mathcal{R}}$
, we obtain for all
$s\in {\mathcal{R}}$
, we obtain for all
![]() $m\geqslant 1$
that
$m\geqslant 1$
that
Therefore,
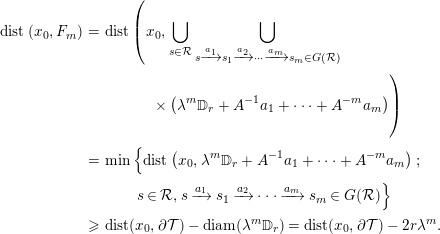 $$\begin{eqnarray}\displaystyle \text{dist}\left(x_{0},F_{m}\right) & = & \displaystyle \text{dist}\left(x_{0},\mathop{\bigcup }_{s\in {\mathcal{R}}}\mathop{\bigcup }_{s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{m}}s_{m}\in G({\mathcal{R}})}\right.\nonumber\\ \displaystyle & & \displaystyle \quad \qquad \left.\times \left(\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r}+A^{-1}a_{1}+\cdots +A^{-m}a_{m}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle \text{min}\left\{\text{dist}\left(x_{0},\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r}+A^{-1}a_{1}+\cdots +A^{-m}a_{m}\right);\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \left.s\in {\mathcal{R}},s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{m}}s_{m}\in G({\mathcal{R}})\right\}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \text{dist}(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})-\text{diam}(\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r})=\text{dist}(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})-2r\unicode[STIX]{x1D706}^{m}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{dist}\left(x_{0},F_{m}\right) & = & \displaystyle \text{dist}\left(x_{0},\mathop{\bigcup }_{s\in {\mathcal{R}}}\mathop{\bigcup }_{s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{m}}s_{m}\in G({\mathcal{R}})}\right.\nonumber\\ \displaystyle & & \displaystyle \quad \qquad \left.\times \left(\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r}+A^{-1}a_{1}+\cdots +A^{-m}a_{m}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle \text{min}\left\{\text{dist}\left(x_{0},\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r}+A^{-1}a_{1}+\cdots +A^{-m}a_{m}\right);\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \left.s\in {\mathcal{R}},s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{m}}s_{m}\in G({\mathcal{R}})\right\}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \text{dist}(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})-\text{diam}(\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r})=\text{dist}(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})-2r\unicode[STIX]{x1D706}^{m}.\nonumber\end{eqnarray}$$
The inequality is justified as follows. Each disk appearing in the lower union of (3.1) intersects
![]() $\unicode[STIX]{x2202}T$
, because
$\unicode[STIX]{x2202}T$
, because
and
![]() $(a_{1},\ldots ,a_{m})$
is a sequence of digits labeling a walk in
$(a_{1},\ldots ,a_{m})$
is a sequence of digits labeling a walk in
![]() $G({\mathcal{R}})$
.
$G({\mathcal{R}})$
.
By this inequality, the assumption that
![]() $x_{0}\notin \unicode[STIX]{x2202}{\mathcal{T}}$
ensures the existence of
$x_{0}\notin \unicode[STIX]{x2202}{\mathcal{T}}$
ensures the existence of
![]() $m\geqslant 1$
such that
$m\geqslant 1$
such that
![]() $\text{dist}(x_{0},F_{m})>0$
. Let
$\text{dist}(x_{0},F_{m})>0$
. Let
![]() $N\geqslant 1$
be the least integer such that
$N\geqslant 1$
be the least integer such that
![]() $x_{0}\notin F_{N}$
.
$x_{0}\notin F_{N}$
.
Now, let
![]() $w:=w_{k}^{(N)}:s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{N}}s_{N}$
be a walk of length
$w:=w_{k}^{(N)}:s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{N}}s_{N}$
be a walk of length
![]() $N$
in
$N$
in
![]() $G({\mathcal{R}})$
for some
$G({\mathcal{R}})$
for some
![]() $1\leqslant k\leqslant m_{N}$
, as defined in Remark 2.5. The associated segment
$1\leqslant k\leqslant m_{N}$
, as defined in Remark 2.5. The associated segment
is a subset of the disk
![]() $F_{w}:=\unicode[STIX]{x1D706}^{N}\mathbb{D}_{r}+A^{-1}a_{1}+\cdots +A^{-N}a_{N}$
, because its endpoints belong to this convex set by (3.2). (We define
$F_{w}:=\unicode[STIX]{x1D706}^{N}\mathbb{D}_{r}+A^{-1}a_{1}+\cdots +A^{-N}a_{N}$
, because its endpoints belong to this convex set by (3.2). (We define
![]() $w_{m_{N}+1}^{(N)}:=w_{1}^{(N)}$
.) Since these segments build up
$w_{m_{N}+1}^{(N)}:=w_{1}^{(N)}$
.) Since these segments build up
![]() $\unicode[STIX]{x1D6E5}_{N}$
, we obtain that
$\unicode[STIX]{x1D6E5}_{N}$
, we obtain that
![]() $\unicode[STIX]{x1D6E5}_{N}\subset F_{N}$
. In particular,
$\unicode[STIX]{x1D6E5}_{N}\subset F_{N}$
. In particular,
Moreover, for any
![]() $w:=s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{N}}s_{N}$
as above and any
$w:=s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{N}}s_{N}$
as above and any
![]() $w^{\prime }:=s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{n}}s_{n}$
with
$w^{\prime }:=s\xrightarrow[{}]{a_{1}}s_{1}\xrightarrow[{}]{a_{2}}\cdots \xrightarrow[{}]{a_{n}}s_{n}$
with
![]() $n\geqslant N$
(that is,
$n\geqslant N$
(that is,
![]() $w^{\prime }$
starts like
$w^{\prime }$
starts like
![]() $w$
), the corresponding segment
$w$
), the corresponding segment
remains in the disk
![]() $F_{w}$
, again by (3.2). It follows that the simple closed curve
$F_{w}$
, again by (3.2). It follows that the simple closed curve
![]() $\unicode[STIX]{x1D6E5}_{n}$
can be obtained by continuous deformation (homotopy) of
$\unicode[STIX]{x1D6E5}_{n}$
can be obtained by continuous deformation (homotopy) of
![]() $\unicode[STIX]{x1D6E5}_{N}$
inside
$\unicode[STIX]{x1D6E5}_{N}$
inside
![]() $F_{N}$
. This homotopy fixes the vertices of
$F_{N}$
. This homotopy fixes the vertices of
![]() $\unicode[STIX]{x1D6E5}_{N}$
.
$\unicode[STIX]{x1D6E5}_{N}$
.
We conclude that for all
![]() $n\geqslant N$
,
$n\geqslant N$
,
This gives an algorithm to compute
![]() $W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
and decide whether
$W(x_{0},\unicode[STIX]{x2202}{\mathcal{T}})$
and decide whether
![]() $x_{0}$
is an inner point of
$x_{0}$
is an inner point of
![]() ${\mathcal{T}}$
or of
${\mathcal{T}}$
or of
![]() $\mathbb{R}\setminus {\mathcal{T}}$
.
$\mathbb{R}\setminus {\mathcal{T}}$
.
Indeed, we can check by computer whether
![]() $x_{0}\in F_{m}$
or
$x_{0}\in F_{m}$
or
![]() $x_{0}\notin F_{m}$
for
$x_{0}\notin F_{m}$
for
![]() $m=1,2,\ldots$
. Note that suitable
$m=1,2,\ldots$
. Note that suitable
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $r$
are computable from the matrix
$r$
are computable from the matrix
![]() $A$
and the digit set
$A$
and the digit set
![]() ${\mathcal{D}}$
. The least
${\mathcal{D}}$
. The least
![]() $m\geqslant 1$
such that
$m\geqslant 1$
such that
![]() $x_{0}\notin F_{m}$
defines
$x_{0}\notin F_{m}$
defines
![]() $N$
. Then, we can compute the winding number
$N$
. Then, we can compute the winding number
![]() $W(x_{0},\unicode[STIX]{x1D6E5}_{N})$
.
$W(x_{0},\unicode[STIX]{x1D6E5}_{N})$
.
![]() $\unicode[STIX]{x1D6E5}_{N}$
is a simple closed polygonal curve, whose vertices are computable because they are images of fixed points of contractions,
$\unicode[STIX]{x1D6E5}_{N}$
is a simple closed polygonal curve, whose vertices are computable because they are images of fixed points of contractions,
where
![]() $f_{a}(x):=A^{-1}(x+a)$
for each
$f_{a}(x):=A^{-1}(x+a)$
for each
![]() $a\in {\mathcal{D}}$
(see Remark 2.5). The value (
$a\in {\mathcal{D}}$
(see Remark 2.5). The value (
![]() $0$
or
$0$
or
![]() $1$
) of this winding number indicates whether
$1$
) of this winding number indicates whether
![]() $x_{0}$
is an inner point of
$x_{0}$
is an inner point of
![]() ${\mathcal{T}}$
or of its complement.◻
${\mathcal{T}}$
or of its complement.◻
Note that without the knowledge of
![]() $x_{0}\not \in \unicode[STIX]{x2202}{\mathcal{T}}$
, there is no algorithm to tell whether a point lies in
$x_{0}\not \in \unicode[STIX]{x2202}{\mathcal{T}}$
, there is no algorithm to tell whether a point lies in
![]() ${\mathcal{T}}$
or not [Reference DubeDub93].
${\mathcal{T}}$
or not [Reference DubeDub93].
4 Outer identifications
Let
![]() $C:[0,1]\rightarrow \unicode[STIX]{x2202}{\mathcal{T}}$
be the parametrization with
$C:[0,1]\rightarrow \unicode[STIX]{x2202}{\mathcal{T}}$
be the parametrization with
![]() $C(0)=C(1)$
.
$C(0)=C(1)$
.
Definition 4.1. A pair
![]() $(a,b)$
with
$(a,b)$
with
![]() $0<a<b<1$
is an identification if
$0<a<b<1$
is an identification if
![]() $C(a)=C(b)$
. Two identifications
$C(a)=C(b)$
. Two identifications
![]() $(a,b)$
and
$(a,b)$
and
![]() $(c,d)$
are crossing if either
$(c,d)$
are crossing if either
![]() $a<c<b<d$
or
$a<c<b<d$
or
![]() $c<a<d<b$
holds.
$c<a<d<b$
holds.
In this paper, we restrict to the case where no pairs of identifications are crossing. This is not the general case, as we mention in Section 7.
In order to classify the identifications, we need to compute the winding number of points with respect to subsets of the boundary
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
. We denote by
$\unicode[STIX]{x2202}{\mathcal{T}}$
. We denote by
![]() $(\unicode[STIX]{x1D6E5}_{n})_{n\geqslant 0}$
the sequence of simple closed polygonal curves approximating
$(\unicode[STIX]{x1D6E5}_{n})_{n\geqslant 0}$
the sequence of simple closed polygonal curves approximating
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
. For each
$\unicode[STIX]{x2202}{\mathcal{T}}$
. For each
![]() $n$
, the vertices of
$n$
, the vertices of
![]() $\unicode[STIX]{x1D6E5}_{n}$
are points
$\unicode[STIX]{x1D6E5}_{n}$
are points
![]() $C(t_{k}^{(n)})\in \unicode[STIX]{x2202}{\mathcal{T}},k\in \{0,\ldots ,m_{n}\},$
where
$C(t_{k}^{(n)})\in \unicode[STIX]{x2202}{\mathcal{T}},k\in \{0,\ldots ,m_{n}\},$
where
![]() $0=t_{0}^{(n)}<t_{1}^{(n)}<\cdots <t_{m_{n}}^{(n)}=1$
. For an identification
$0=t_{0}^{(n)}<t_{1}^{(n)}<\cdots <t_{m_{n}}^{(n)}=1$
. For an identification
![]() $(a,b)$
, we define
$(a,b)$
, we define
Note that
![]() $(a_{n})_{n\geqslant 0}$
is increasing and converges to
$(a_{n})_{n\geqslant 0}$
is increasing and converges to
![]() $a$
, whereas
$a$
, whereas
![]() $(b_{n})_{n\geqslant 0}$
is decreasing and converges to
$(b_{n})_{n\geqslant 0}$
is decreasing and converges to
![]() $b$
. Let us consider
$b$
. Let us consider
-
(i)
 $C_{n}(a_{n},b_{n})$
, the closed polygonal curve obtained by joining the points
$C_{n}(a_{n},b_{n})$
, the closed polygonal curve obtained by joining the points
 $C(t_{k}^{(n)})$
consecutively for
$C(t_{k}^{(n)})$
consecutively for
 $a_{n}\leqslant t_{k}^{(n)}\leqslant b_{n}$
, and adding the segment
$a_{n}\leqslant t_{k}^{(n)}\leqslant b_{n}$
, and adding the segment
 $[C(b_{n}),C(a_{n})]$
;
$[C(b_{n}),C(a_{n})]$
; -
(ii)
 $D_{n}(a_{n},b_{n})$
, the closed polygonal curve
$D_{n}(a_{n},b_{n})$
, the closed polygonal curve  $$\begin{eqnarray}D_{n}(a_{n},b_{n})=\left(\unicode[STIX]{x1D6E5}_{n}\setminus C_{n}(a_{n},b_{n})\right)\,\cup \,[C(b_{n}),C(a_{n})].\end{eqnarray}$$
$$\begin{eqnarray}D_{n}(a_{n},b_{n})=\left(\unicode[STIX]{x1D6E5}_{n}\setminus C_{n}(a_{n},b_{n})\right)\,\cup \,[C(b_{n}),C(a_{n})].\end{eqnarray}$$
The curve
![]() $C_{n}(a_{n},b_{n})\setminus ]\!C(b_{n}),C(a_{n})\![$
is a subset of
$C_{n}(a_{n},b_{n})\setminus ]\!C(b_{n}),C(a_{n})\![$
is a subset of
![]() $\unicode[STIX]{x1D6E5}_{n}$
; thus,
$\unicode[STIX]{x1D6E5}_{n}$
; thus,
![]() $C_{n}(a_{n},b_{n})$
may intersect itself only along the added segment
$C_{n}(a_{n},b_{n})$
may intersect itself only along the added segment
![]() $[C(b_{n}),C(a_{n})]$
. This also holds for
$[C(b_{n}),C(a_{n})]$
. This also holds for
![]() $D_{n}(a_{n},b_{n})$
. Moreover, in the Hausdorff metric,
$D_{n}(a_{n},b_{n})$
. Moreover, in the Hausdorff metric,
![]() $(C_{n}(a_{n},b_{n}))_{n\geqslant 0}$
converges to
$(C_{n}(a_{n},b_{n}))_{n\geqslant 0}$
converges to
![]() $C([a,b])$
, while
$C([a,b])$
, while
![]() $(D_{n}(a_{n},b_{n}))_{n\geqslant 0}$
converges to
$(D_{n}(a_{n},b_{n}))_{n\geqslant 0}$
converges to
![]() $C([0,a])\cup C([b,1])$
.
$C([0,a])\cup C([b,1])$
.
Lemma 4.2. Let
![]() $y\in \mathbb{R}^{2}\setminus C([a,b])$
. Then, the sequence
$y\in \mathbb{R}^{2}\setminus C([a,b])$
. Then, the sequence
![]() $(W(y,C_{n}(a_{n},b_{n})))_{n\geqslant 0}$
is eventually well-defined and constant of value either
$(W(y,C_{n}(a_{n},b_{n})))_{n\geqslant 0}$
is eventually well-defined and constant of value either
![]() $0$
or
$0$
or
![]() $1$
.
$1$
.
Proof. We denote by
![]() $\text{dist}_{H}(A,B)$
the Hausdorff distance between two nonempty compact sets
$\text{dist}_{H}(A,B)$
the Hausdorff distance between two nonempty compact sets
![]() $A,B$
of
$A,B$
of
![]() $\mathbb{R}^{2}$
. Let
$\mathbb{R}^{2}$
. Let
![]() $y\in \mathbb{R}^{2}\setminus C([a,b])$
, and let
$y\in \mathbb{R}^{2}\setminus C([a,b])$
, and let
![]() $\unicode[STIX]{x1D716}>0$
, such that
$\unicode[STIX]{x1D716}>0$
, such that
![]() $\text{dist}_{H}(\{y\},C([a,b]))>\unicode[STIX]{x1D716}$
. Let us choose integers as follows.
$\text{dist}_{H}(\{y\},C([a,b]))>\unicode[STIX]{x1D716}$
. Let us choose integers as follows.
-
∙
 $N_{1}$
such that the Hausdorff distances are at most
$N_{1}$
such that the Hausdorff distances are at most $$\begin{eqnarray}\displaystyle & & \displaystyle \text{dist}_{H}(\unicode[STIX]{x1D6E5}_{n},\unicode[STIX]{x2202}{\mathcal{T}}),\quad \text{dist}_{H}(C_{n}(a_{n},b_{n}),C([a,b])),\quad \nonumber\\ \displaystyle & & \displaystyle \text{dist}_{H}(D_{n}(a_{n},b_{n}),C([0,a])\cup C([b,1]))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{dist}_{H}(\unicode[STIX]{x1D6E5}_{n},\unicode[STIX]{x2202}{\mathcal{T}}),\quad \text{dist}_{H}(C_{n}(a_{n},b_{n}),C([a,b])),\quad \nonumber\\ \displaystyle & & \displaystyle \text{dist}_{H}(D_{n}(a_{n},b_{n}),C([0,a])\cup C([b,1]))\nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D716}/4$
for all
$\unicode[STIX]{x1D716}/4$
for all
 $n\geqslant N_{1}$
.
$n\geqslant N_{1}$
.
-
∙
 $N_{2}$
such that for all
$N_{2}$
such that for all
 $n\geqslant N_{2}$
, the points
$n\geqslant N_{2}$
, the points
 $C(a_{n})$
and
$C(a_{n})$
and
 $C(b_{n})$
belong to the disk
$C(b_{n})$
belong to the disk
 $\mathbb{D}(C(a);\unicode[STIX]{x1D716}/4)$
of center
$\mathbb{D}(C(a);\unicode[STIX]{x1D716}/4)$
of center
 $C(a)=C(b)$
and radius
$C(a)=C(b)$
and radius
 $\unicode[STIX]{x1D716}/4$
.
$\unicode[STIX]{x1D716}/4$
.
Let
![]() $N:=\text{max}\{N_{1},N_{2}\}$
. Note that, by assumption,
$N:=\text{max}\{N_{1},N_{2}\}$
. Note that, by assumption,
![]() $y$
belongs to
$y$
belongs to
![]() $\mathbb{R}^{2}\setminus C_{n}(a_{n},b_{n})$
for all
$\mathbb{R}^{2}\setminus C_{n}(a_{n},b_{n})$
for all
![]() $n\geqslant N$
.
$n\geqslant N$
.
We now fix
![]() $n\geqslant N$
. We show that
$n\geqslant N$
. We show that
![]() $C_{n+1}(a_{n+1},b_{n+1})$
is obtained from
$C_{n+1}(a_{n+1},b_{n+1})$
is obtained from
![]() $C_{n}(a_{n},b_{n})$
by continuous deformation (homotopy) avoiding
$C_{n}(a_{n},b_{n})$
by continuous deformation (homotopy) avoiding
![]() $y$
. Indeed, the simple polygonal arcs
$y$
. Indeed, the simple polygonal arcs
are at most at
![]() $\unicode[STIX]{x1D716}/2$
-Hausdorff distance from each other; thus, there is a homotopy between these arcs that does not intersect the disk
$\unicode[STIX]{x1D716}/2$
-Hausdorff distance from each other; thus, there is a homotopy between these arcs that does not intersect the disk
![]() $\mathbb{D}(y;\unicode[STIX]{x1D716}/4)$
. Moreover, there exists a homotopy between the segments
$\mathbb{D}(y;\unicode[STIX]{x1D716}/4)$
. Moreover, there exists a homotopy between the segments
inside the disk
![]() $\mathbb{D}(C(a);\unicode[STIX]{x1D716}/2)$
, thus avoiding the disk
$\mathbb{D}(C(a);\unicode[STIX]{x1D716}/2)$
, thus avoiding the disk
![]() $\mathbb{D}(y;\unicode[STIX]{x1D716}/4)$
.
$\mathbb{D}(y;\unicode[STIX]{x1D716}/4)$
.
We infer the existence of a homotopy between the polygonal curves
![]() $C_{n}(a_{n},b_{n})$
and
$C_{n}(a_{n},b_{n})$
and
![]() $C_{n+1}(a_{n+1},b_{n+1})$
that avoids the point
$C_{n+1}(a_{n+1},b_{n+1})$
that avoids the point
![]() $y$
. Therefore, the winding number remains constant:
$y$
. Therefore, the winding number remains constant:
for all
![]() $n\geqslant N$
.
$n\geqslant N$
.
We finally show that the winding number for
![]() $n=N$
is either
$n=N$
is either
![]() $0$
or
$0$
or
![]() $1$
. This is due to the fact that
$1$
. This is due to the fact that
![]() $y$
lies outside the disk
$y$
lies outside the disk
![]() $\mathbb{D}(C(a);\unicode[STIX]{x1D716}/4)$
where the polygonal closed curve
$\mathbb{D}(C(a);\unicode[STIX]{x1D716}/4)$
where the polygonal closed curve
![]() $C_{N}(a_{N},b_{N})$
may intersect itself.◻
$C_{N}(a_{N},b_{N})$
may intersect itself.◻
A similar result holds for the winding numbers with respect to
![]() $D_{n}(a_{n},b_{n})$
.
$D_{n}(a_{n},b_{n})$
.
Lemma 4.3. Let
![]() $y\in \mathbb{R}^{2}\setminus \left(C([0,a])\cup C([b,1])\right)$
. Then, the sequence
$y\in \mathbb{R}^{2}\setminus \left(C([0,a])\cup C([b,1])\right)$
. Then, the sequence
![]() $(W(y,D_{n}(a_{n},b_{n})))_{n\geqslant 0}$
is eventually well-defined and constant of value either
$(W(y,D_{n}(a_{n},b_{n})))_{n\geqslant 0}$
is eventually well-defined and constant of value either
![]() $0$
or
$0$
or
![]() $1$
.
$1$
.
By the above lemmata, we can define the winding numbers
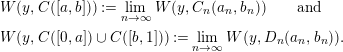 $$\begin{eqnarray}\displaystyle & & \displaystyle W(y,C([a,b])):=\lim _{n\rightarrow \infty }W(y,C_{n}(a_{n},b_{n}))\qquad \text{and}\quad \nonumber\\ \displaystyle & & \displaystyle W(y,C([0,a])\cup C([b,1])):=\lim _{n\rightarrow \infty }W(y,D_{n}(a_{n},b_{n})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle W(y,C([a,b])):=\lim _{n\rightarrow \infty }W(y,C_{n}(a_{n},b_{n}))\qquad \text{and}\quad \nonumber\\ \displaystyle & & \displaystyle W(y,C([0,a])\cup C([b,1])):=\lim _{n\rightarrow \infty }W(y,D_{n}(a_{n},b_{n})).\nonumber\end{eqnarray}$$
The next lemma asserts that the winding numbers defined with respect to the above fractal curves have the same expected properties as winding numbers with respect to polygonal curves.
Lemma 4.4. Let
![]() $L$
be either the curve
$L$
be either the curve
![]() $C([a,b])$
or the curve
$C([a,b])$
or the curve
![]() $C([0,a])\cup C([b,1])$
. Let
$C([0,a])\cup C([b,1])$
. Let
![]() $x,y\in \mathbb{R}^{2}$
belong to the same connected component of
$x,y\in \mathbb{R}^{2}$
belong to the same connected component of
![]() $\mathbb{R}^{2}\setminus L$
. Then,
$\mathbb{R}^{2}\setminus L$
. Then,
Proof. In the following, for
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
![]() $L_{n}$
denotes the polygonal curve
$L_{n}$
denotes the polygonal curve
![]() $C_{n}(a_{n},b_{n})$
in the case
$C_{n}(a_{n},b_{n})$
in the case
![]() $L=C([a,b])$
) and the polygonal curve
$L=C([a,b])$
) and the polygonal curve
![]() $D_{n}(a_{n},b_{n})$
in the case
$D_{n}(a_{n},b_{n})$
in the case
![]() $L=C([0,a])\cup C([b,1])$
.
$L=C([0,a])\cup C([b,1])$
.
By Lemmas 4.2 and 4.3, there exists
![]() $n_{0}$
such that, for all
$n_{0}$
such that, for all
![]() $n\geqslant n_{0}$
, we have
$n\geqslant n_{0}$
, we have
Since
![]() $x$
and
$x$
and
![]() $y$
belong to the same component
$y$
belong to the same component
![]() $U$
of
$U$
of
![]() $\mathbb{R}^{2}\setminus L$
, there exists a simple arc
$\mathbb{R}^{2}\setminus L$
, there exists a simple arc
![]() $l:[0,1]\rightarrow U$
satisfying
$l:[0,1]\rightarrow U$
satisfying
![]() $l(0)=x$
and
$l(0)=x$
and
![]() $l(1)=y$
. Let
$l(1)=y$
. Let
![]() $\unicode[STIX]{x1D716}>0$
, such that
$\unicode[STIX]{x1D716}>0$
, such that
![]() $\text{dist}_{H}(l([0,1]),L)>\unicode[STIX]{x1D716}$
. Remember that
$\text{dist}_{H}(l([0,1]),L)>\unicode[STIX]{x1D716}$
. Remember that
![]() $(L_{n})_{n\geqslant 0}$
converges to
$(L_{n})_{n\geqslant 0}$
converges to
![]() $L$
in Hausdorff distance. Thus, there exists
$L$
in Hausdorff distance. Thus, there exists
![]() $n_{1}\geqslant n_{0}$
satisfying
$n_{1}\geqslant n_{0}$
satisfying
Therefore,
![]() $x$
and
$x$
and
![]() $y$
belong to the same connected component of
$y$
belong to the same connected component of
![]() $\mathbb{R}^{2}\setminus L_{n_{1}}$
. As
$\mathbb{R}^{2}\setminus L_{n_{1}}$
. As
![]() $L_{n_{1}}$
is a polygonal curve, this implies that
$L_{n_{1}}$
is a polygonal curve, this implies that
![]() $W(x,L_{n_{1}})=W(y,L_{n_{1}})$
, and hence that
$W(x,L_{n_{1}})=W(y,L_{n_{1}})$
, and hence that
![]() $W(x,L)=W(y,L)$
.◻
$W(x,L)=W(y,L)$
.◻
Since we assume that no pairs of identifications are crossing, the following proposition holds (see Figure 1).

Figure 1. Proposition 4.5. In the above two cases,
![]() $C([a,b])$
is shown solid and
$C([a,b])$
is shown solid and
![]() $C([0,a])\cup C([b,1])$
is shown dashed. The intersection point is
$C([0,a])\cup C([b,1])$
is shown dashed. The intersection point is
![]() $C(a)=C(b)$
.
$C(a)=C(b)$
.
Proposition 4.5. There exist
![]() $w_{a,b},w_{a,b}^{\prime }\in \{0,1\}$
such that for all
$w_{a,b},w_{a,b}^{\prime }\in \{0,1\}$
such that for all
![]() $t\in [0,a)\cup (b,1]$
and for all
$t\in [0,a)\cup (b,1]$
and for all
![]() $t^{\prime }\in (a,b)$
,
$t^{\prime }\in (a,b)$
,
Proof. We call
![]() $K:=C([a,b])$
and
$K:=C([a,b])$
and
![]() $J:=C([0,a]\cup [b,1])$
the connected subcurves of
$J:=C([0,a]\cup [b,1])$
the connected subcurves of
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
. By the noncrossing assumption, we have
$\unicode[STIX]{x2202}{\mathcal{T}}$
. By the noncrossing assumption, we have
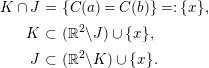 $$\begin{eqnarray}\displaystyle K\cap J & = & \displaystyle \{C(a)=C(b)\}=:\{x\},\nonumber\\ \displaystyle K & \subset & \displaystyle (\mathbb{R}^{2}\setminus J)\cup \{x\},\nonumber\\ \displaystyle J & \subset & \displaystyle (\mathbb{R}^{2}\setminus K)\cup \{x\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K\cap J & = & \displaystyle \{C(a)=C(b)\}=:\{x\},\nonumber\\ \displaystyle K & \subset & \displaystyle (\mathbb{R}^{2}\setminus J)\cup \{x\},\nonumber\\ \displaystyle J & \subset & \displaystyle (\mathbb{R}^{2}\setminus K)\cup \{x\}.\nonumber\end{eqnarray}$$
Note that
![]() $K\setminus \{x\}=C((a,b))$
; hence, this set is connected. Similarly,
$K\setminus \{x\}=C((a,b))$
; hence, this set is connected. Similarly,
![]() $J\setminus \{x\}$
is connected. We call
$J\setminus \{x\}$
is connected. We call
-
∙
 $U$
the connected component of
$U$
the connected component of
 $\mathbb{R}^{2}\setminus J$
such that
$\mathbb{R}^{2}\setminus J$
such that
 $K\setminus \{x\}\subset U$
;
$K\setminus \{x\}\subset U$
; -
∙
 $V$
the connected component of
$V$
the connected component of
 $\mathbb{R}^{2}\setminus K$
such that
$\mathbb{R}^{2}\setminus K$
such that
 $J\setminus \{x\}\subset V$
.
$J\setminus \{x\}\subset V$
.
In particular,
![]() $K\subset U\cup \{x\}$
and
$K\subset U\cup \{x\}$
and
![]() $J\subset V\cup \{x\}$
. The proposition now follows from Lemma 4.4.◻
$J\subset V\cup \{x\}$
. The proposition now follows from Lemma 4.4.◻
Definition 4.6. Let
![]() $(a,b)$
be an identification, and let
$(a,b)$
be an identification, and let
![]() $w_{a,b}$
be as in Proposition 4.5. We say that
$w_{a,b}$
be as in Proposition 4.5. We say that
![]() $(a,b)$
is an outer identification if
$(a,b)$
is an outer identification if
![]() $w_{a,b}=w_{a,b}^{\prime }=0$
.
$w_{a,b}=w_{a,b}^{\prime }=0$
.
This case is illustrated on the left side of Figure 1.
Theorem 2. Given an identification of
![]() $C$
, we can decide whether it is an outer identification by an algorithm.
$C$
, we can decide whether it is an outer identification by an algorithm.
Proof. We show that we can compute
![]() $w_{a,b}$
(and similarly
$w_{a,b}$
(and similarly
![]() $w_{a,b}^{\prime }$
) by an algorithm. This is proved by a slight modification of the proof of Theorem 1. Let
$w_{a,b}^{\prime }$
) by an algorithm. This is proved by a slight modification of the proof of Theorem 1. Let
![]() $y:=C(t)$
for some
$y:=C(t)$
for some
![]() $t\in [0,a)\cup (b,1]$
. Let
$t\in [0,a)\cup (b,1]$
. Let
![]() $u_{n},v_{n}$
be the walks in
$u_{n},v_{n}$
be the walks in
![]() $G({\mathcal{R}}^{o})$
satisfying
$G({\mathcal{R}}^{o})$
satisfying
Here,
![]() $\unicode[STIX]{x1D719}^{(1)}$
is the Dumont–Thomas number system defined on p. 5. Let
$\unicode[STIX]{x1D719}^{(1)}$
is the Dumont–Thomas number system defined on p. 5. Let
![]() $k,\unicode[STIX]{x1D706},r$
be as in the proof of Theorem 1. Again, we assume, without loss of generality, that
$k,\unicode[STIX]{x1D706},r$
be as in the proof of Theorem 1. Again, we assume, without loss of generality, that
![]() $k=1$
. Then, for all
$k=1$
. Then, for all
![]() $m\geqslant 1$
,
$m\geqslant 1$
,
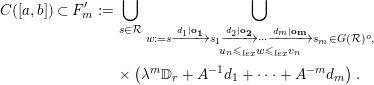 $$\begin{eqnarray}\displaystyle C([a,b])\subset F_{m}^{\prime } & := & \displaystyle \mathop{\bigcup }_{s\in {\mathcal{R}}}\mathop{\bigcup }_{\substack{ w:=s\xrightarrow[{}]{d_{1}|\mathbf{o}_{\mathbf{1}}}s_{1}\xrightarrow[{}]{d_{2}|\mathbf{o}_{\mathbf{2}}}\cdots \xrightarrow[{}]{d_{m}|\mathbf{o}_{\mathbf{m}}}s_{m}\in G({\mathcal{R}})^{o}, \\ {u_{n}\leqslant }_{lex}w\leqslant _{lex}v_{n}}}\nonumber\\ \displaystyle & & \displaystyle \times \left(\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r}+A^{-1}d_{1}+\cdots +A^{-m}d_{m}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C([a,b])\subset F_{m}^{\prime } & := & \displaystyle \mathop{\bigcup }_{s\in {\mathcal{R}}}\mathop{\bigcup }_{\substack{ w:=s\xrightarrow[{}]{d_{1}|\mathbf{o}_{\mathbf{1}}}s_{1}\xrightarrow[{}]{d_{2}|\mathbf{o}_{\mathbf{2}}}\cdots \xrightarrow[{}]{d_{m}|\mathbf{o}_{\mathbf{m}}}s_{m}\in G({\mathcal{R}})^{o}, \\ {u_{n}\leqslant }_{lex}w\leqslant _{lex}v_{n}}}\nonumber\\ \displaystyle & & \displaystyle \times \left(\unicode[STIX]{x1D706}^{m}\mathbb{D}_{r}+A^{-1}d_{1}+\cdots +A^{-m}d_{m}\right).\nonumber\end{eqnarray}$$
The following arguments from the proof of Theorem 1 remain valid:
and we call
![]() $N\geqslant 1$
the least integer satisfying
$N\geqslant 1$
the least integer satisfying
![]() $y\notin F_{N}^{\prime }$
. Then,
$y\notin F_{N}^{\prime }$
. Then,
![]() $\text{dist}(y,C_{N}(a_{N},b_{N}))>0$
, because
$\text{dist}(y,C_{N}(a_{N},b_{N}))>0$
, because
![]() $C_{N}(a_{N},b_{N})\subset F_{N}^{\prime }$
. Moreover, for any
$C_{N}(a_{N},b_{N})\subset F_{N}^{\prime }$
. Moreover, for any
![]() $n\geqslant N$
, the simple polygonal path
$n\geqslant N$
, the simple polygonal path
![]() $C_{n}(a_{n},b_{n})\setminus [C(a_{n}),C(b_{n})]$
(as well as the segment
$C_{n}(a_{n},b_{n})\setminus [C(a_{n}),C(b_{n})]$
(as well as the segment
![]() $[C(a_{n}),C(b_{n})]$
) can be obtained by continuous deformation (homotopy) of
$[C(a_{n}),C(b_{n})]$
) can be obtained by continuous deformation (homotopy) of
![]() $C_{N}(a_{N},b_{N})\setminus [C(a_{N}),C(b_{N})]$
(or of the segment
$C_{N}(a_{N},b_{N})\setminus [C(a_{N}),C(b_{N})]$
(or of the segment
![]() $[C(a_{N}),C(b_{N})]$
, respectively) inside
$[C(a_{N}),C(b_{N})]$
, respectively) inside
![]() $F_{N}^{\prime }$
. These homotopies fix the vertices of
$F_{N}^{\prime }$
. These homotopies fix the vertices of
![]() $C_{N}(a_{N},b_{N})$
.
$C_{N}(a_{N},b_{N})$
.
We conclude that for all
![]() $n\geqslant N$
,
$n\geqslant N$
,
The algorithm for the computation of
![]() $w_{a,b}=W(y,C([a,b]))$
reads as follows. We can check by computer whether
$w_{a,b}=W(y,C([a,b]))$
reads as follows. We can check by computer whether
![]() $y\in F_{m}^{\prime }$
or not for
$y\in F_{m}^{\prime }$
or not for
![]() $m=1,2,\ldots .$
The least
$m=1,2,\ldots .$
The least
![]() $m\geqslant 1$
such that
$m\geqslant 1$
such that
![]() $y\notin F_{m}^{\prime }$
defines
$y\notin F_{m}^{\prime }$
defines
![]() $N$
. Then, we compute the winding number
$N$
. Then, we compute the winding number
![]() $W(y,C_{n}(a_{n},b_{n}))$
of
$W(y,C_{n}(a_{n},b_{n}))$
of
![]() $y$
with respect to the closed polygonal curve
$y$
with respect to the closed polygonal curve
![]() $C_{n}(a_{n},b_{n})$
. Its value is equal to
$C_{n}(a_{n},b_{n})$
. Its value is equal to
![]() $w_{a,b}$
.◻
$w_{a,b}$
.◻
5 Connected components of
 ${\mathcal{T}}^{\circ }$
${\mathcal{T}}^{\circ }$
In this section, we show that the set of outer identifications is in one to one correspondence with the set of connected components of
![]() ${\mathcal{T}}^{\circ }$
.
${\mathcal{T}}^{\circ }$
.
Theorem 3. Suppose that there are no crossing pairs of identifications. Moreover, let
![]() $(a,b)$
and
$(a,b)$
and
![]() $(c,d)$
be two outer identifications with
$(c,d)$
be two outer identifications with
![]() $a<c<d<b$
such that there is no further identification
$a<c<d<b$
such that there is no further identification
![]() $(x,y)$
with
$(x,y)$
with
![]() $a<x<y<c$
,
$a<x<y<c$
,
![]() $d<x<y<b$
or
$d<x<y<b$
or
![]() $a<x<c<d<y<b$
. Then,
$a<x<c<d<y<b$
. Then,
![]() $C([a,c])\cup C([d,b])$
is a simple closed curve, and it is the boundary of a connected component of
$C([a,c])\cup C([d,b])$
is a simple closed curve, and it is the boundary of a connected component of
![]() ${\mathcal{T}}^{\circ }$
. Therefore, the closure of this component is homeomorphic to a closed disk.
${\mathcal{T}}^{\circ }$
. Therefore, the closure of this component is homeomorphic to a closed disk.
This theorem is illustrated in Figure 2.

Figure 2. Theorem 3.
![]() $C([a,c])$
is shown dotted and
$C([a,c])$
is shown dotted and
![]() $C([d,b])$
is shown dashed. The intersection points correspond to
$C([d,b])$
is shown dashed. The intersection points correspond to
![]() $C(a)=C(b)$
and
$C(a)=C(b)$
and
![]() $C(c)=C(d)$
.
$C(c)=C(d)$
.
Proof. By assumption, the parametrization
![]() $C$
is injective on each segment
$C$
is injective on each segment
![]() $[a,c]$
and
$[a,c]$
and
![]() $[d,b]$
, and the simple closed arcs
$[d,b]$
, and the simple closed arcs
![]() $C([a,c])$
and
$C([a,c])$
and
![]() $C([d,b])$
meet only at the points
$C([d,b])$
meet only at the points
![]() $C(a)=C(b)$
and
$C(a)=C(b)$
and
![]() $C(c)=C(d)$
. It follows that
$C(c)=C(d)$
. It follows that
![]() $C([a,c])\cup C([d,b])$
is a simple closed curve.
$C([a,c])\cup C([d,b])$
is a simple closed curve.
We call this curve
![]() $L$
, and call its bounded complementary component
$L$
, and call its bounded complementary component
![]() $B$
. Then,
$B$
. Then,
![]() $L=\unicode[STIX]{x2202}B$
by Jordan’s curve theorem. Let us show in two steps that
$L=\unicode[STIX]{x2202}B$
by Jordan’s curve theorem. Let us show in two steps that
![]() $B\subset \text{int}({\mathcal{T}})$
.
$B\subset \text{int}({\mathcal{T}})$
.
-
(1) We prove that
 $B\cap \unicode[STIX]{x2202}{\mathcal{T}}=\emptyset$
. Otherwise, there is
$B\cap \unicode[STIX]{x2202}{\mathcal{T}}=\emptyset$
. Otherwise, there is
 $t$
such that and, by definition,
$t$
such that and, by definition, $$\begin{eqnarray}x_{0}:=C(t)\in B\cap \unicode[STIX]{x2202}{\mathcal{T}},\end{eqnarray}$$
$$\begin{eqnarray}x_{0}:=C(t)\in B\cap \unicode[STIX]{x2202}{\mathcal{T}},\end{eqnarray}$$
 $t\in [0,a)\cup (c,d)\cup (b,1]$
. First, suppose that
$t\in [0,a)\cup (c,d)\cup (b,1]$
. First, suppose that
 $t\in [0,a)\cup (b,1]$
. By our assumptions, we can apply Proposition 4.5 and obtain that However, since
$t\in [0,a)\cup (b,1]$
. By our assumptions, we can apply Proposition 4.5 and obtain that However, since $$\begin{eqnarray}W(x_{0},C([a,b]))=w_{a,b}=0=w_{c,d}=W(x_{0},C([c,d])).\end{eqnarray}$$
$$\begin{eqnarray}W(x_{0},C([a,b]))=w_{a,b}=0=w_{c,d}=W(x_{0},C([c,d])).\end{eqnarray}$$
 $x_{0}$
is in the bounded component of the simple closed curve
$x_{0}$
is in the bounded component of the simple closed curve
 $L$
, its winding number with respect to
$L$
, its winding number with respect to
 $L$
is
$L$
is
 $W(x_{0},L)=1$
. It follows that a contradiction. Hence,
$W(x_{0},L)=1$
. It follows that a contradiction. Hence, $$\begin{eqnarray}0=W(x_{0},C([a,b]))=W(x_{0},C([c,d]))+W(x_{0},L)=0+1=1,\end{eqnarray}$$
$$\begin{eqnarray}0=W(x_{0},C([a,b]))=W(x_{0},C([c,d]))+W(x_{0},L)=0+1=1,\end{eqnarray}$$
 $t\notin [0,a)\cup (b,1]$
. In the same way, using the fact that
$t\notin [0,a)\cup (b,1]$
. In the same way, using the fact that
 $w_{a,b}^{\prime }=w_{c,d}^{\prime }=0$
, one can prove that
$w_{a,b}^{\prime }=w_{c,d}^{\prime }=0$
, one can prove that
 $t\notin (c,d)$
. Therefore, we conclude that
$t\notin (c,d)$
. Therefore, we conclude that
 $B\cap \unicode[STIX]{x2202}{\mathcal{T}}=\emptyset$
.
$B\cap \unicode[STIX]{x2202}{\mathcal{T}}=\emptyset$
.
-
(2) We prove that
 $B\cap \text{int}({\mathcal{T}})\neq \emptyset$
. Suppose, on the contrary, that
$B\cap \text{int}({\mathcal{T}})\neq \emptyset$
. Suppose, on the contrary, that
 $B\cap \text{int}({\mathcal{T}})=\emptyset$
. Let
$B\cap \text{int}({\mathcal{T}})=\emptyset$
. Let
 $x\in L\setminus \{C(a)=C(b)\}$
, and let
$x\in L\setminus \{C(a)=C(b)\}$
, and let
 $\unicode[STIX]{x1D716}>0$
, such that Since
$\unicode[STIX]{x1D716}>0$
, such that Since $$\begin{eqnarray}\mathbb{D}(x,\unicode[STIX]{x1D716})\cap C([0,a]\cup [b,1])=\mathbb{D}(x,\unicode[STIX]{x1D716})\cap C([c,d])=\emptyset .\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{D}(x,\unicode[STIX]{x1D716})\cap C([0,a]\cup [b,1])=\mathbb{D}(x,\unicode[STIX]{x1D716})\cap C([c,d])=\emptyset .\end{eqnarray}$$
 $L\subset \unicode[STIX]{x2202}{\mathcal{T}}$
, we have that
$L\subset \unicode[STIX]{x2202}{\mathcal{T}}$
, we have that
 $\text{int}({\mathcal{T}})\cap \mathbb{D}(x,\unicode[STIX]{x1D716})\neq \emptyset$
. Let
$\text{int}({\mathcal{T}})\cap \mathbb{D}(x,\unicode[STIX]{x1D716})\neq \emptyset$
. Let
 $z$
be in this intersection. Then, by assumption,
$z$
be in this intersection. Then, by assumption,
 $z$
is in the unbounded complementary component of the simple closed curve
$z$
is in the unbounded complementary component of the simple closed curve
 $L$
; hence,
$L$
; hence,
 $W(z,L)=0$
. Moreover, and
$W(z,L)=0$
. Moreover, and $$\begin{eqnarray}W(z,C([0,a]\cup [b,1]))=W(x,C([0,a]\cup [b,1]))=w_{a,b}^{\prime }=0\end{eqnarray}$$
We use here the fact that
$$\begin{eqnarray}W(z,C([0,a]\cup [b,1]))=W(x,C([0,a]\cup [b,1]))=w_{a,b}^{\prime }=0\end{eqnarray}$$
We use here the fact that $$\begin{eqnarray}W(z,C([c,d]))=W(x,C([c,d]))=w_{c,d}=0.\end{eqnarray}$$
$$\begin{eqnarray}W(z,C([c,d]))=W(x,C([c,d]))=w_{c,d}=0.\end{eqnarray}$$
 $(a,b)$
and
$(a,b)$
and
 $(c,d)$
are outer identifications. Therefore, However, since
$(c,d)$
are outer identifications. Therefore, However, since $$\begin{eqnarray}W(z,\unicode[STIX]{x2202}{\mathcal{T}})=W(z,C([0,a]\cup [b,1]))+W(z,L)+W(z,C([c,d]))=0.\end{eqnarray}$$
$$\begin{eqnarray}W(z,\unicode[STIX]{x2202}{\mathcal{T}})=W(z,C([0,a]\cup [b,1]))+W(z,L)+W(z,C([c,d]))=0.\end{eqnarray}$$
 $z$
is an inner point of
$z$
is an inner point of
 ${\mathcal{T}}$
, we have
${\mathcal{T}}$
, we have
 $W(z,\unicode[STIX]{x2202}{\mathcal{T}})=1$
, a contradiction. We conclude that
$W(z,\unicode[STIX]{x2202}{\mathcal{T}})=1$
, a contradiction. We conclude that
 $B\cap \text{int}({\mathcal{T}})\neq \emptyset$
.
$B\cap \text{int}({\mathcal{T}})\neq \emptyset$
.
This proves that
![]() $B\subset \text{int}({\mathcal{T}})$
. Consequently,
$B\subset \text{int}({\mathcal{T}})$
. Consequently,
![]() $B$
is a connected component of
$B$
is a connected component of
![]() $\text{int}({\mathcal{T}})$
, as it is an open connected set of
$\text{int}({\mathcal{T}})$
, as it is an open connected set of
![]() $\text{int}({\mathcal{T}})$
whose boundary is a subset of
$\text{int}({\mathcal{T}})$
whose boundary is a subset of
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
. The fact that its closure is a topological disk follows from the theorem of Schönflies.◻
$\unicode[STIX]{x2202}{\mathcal{T}}$
. The fact that its closure is a topological disk follows from the theorem of Schönflies.◻
6 An example from Bandt and Gelbrich
This example can be found in [Reference Bandt and GelbrichBG94] and [Reference Bandt and WangBW01, Figure 4]. We depict it with its neighbors in Figure 3.

Figure 3. Example of Bandt and Gelbrich and its lattice tiling.

Figure 4. Boundary graph of the example of Bandt and Gelbrich.
The tile
![]() ${\mathcal{T}}$
satisfies the equation
${\mathcal{T}}$
satisfies the equation
where
The tile
![]() ${\mathcal{T}}$
has the following neighbors:
${\mathcal{T}}$
has the following neighbors:
The contact automaton and the boundary automaton can be computed via well-known algorithms (see, for example, [Reference Scheicher and ThuswaldnerST03]). The boundary automaton
![]() $G({\mathcal{S}})$
is depicted in Figure 4. The contact automaton
$G({\mathcal{S}})$
is depicted in Figure 4. The contact automaton
![]() $G({\mathcal{R}})$
is the restriction of the boundary automaton to the set
$G({\mathcal{R}})$
is the restriction of the boundary automaton to the set
As
![]() $G({\mathcal{R}})$
is the contact automaton of
$G({\mathcal{R}})$
is the contact automaton of
![]() ${\mathcal{T}}(A,{\mathcal{D}})$
,
${\mathcal{T}}(A,{\mathcal{D}})$
,
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
is the solution of the GIFS (2.1). Since
$\unicode[STIX]{x2202}{\mathcal{T}}$
is the solution of the GIFS (2.1). Since
![]() $\text{det}(A)<0$
, the orientation of the boundary pieces changes at each iteration of (2.1). We model this flipping by doubling the number of states of the contact automaton (see also [Reference Akiyama and LoridantAL10, Section 2]) as follows.
$\text{det}(A)<0$
, the orientation of the boundary pieces changes at each iteration of (2.1). We model this flipping by doubling the number of states of the contact automaton (see also [Reference Akiyama and LoridantAL10, Section 2]) as follows.
-
∙ For each state
 $s\in {\mathcal{R}}$
, we create the states
$s\in {\mathcal{R}}$
, we create the states
 $s$
and
$s$
and
 $\overline{s}$
.
$\overline{s}$
. -
∙ For each transition
 $s\xrightarrow[{}]{a|a^{\prime }}s^{\prime }\in G({\mathcal{R}})$
, we create the transitions
$s\xrightarrow[{}]{a|a^{\prime }}s^{\prime }\in G({\mathcal{R}})$
, we create the transitions
 $s\xrightarrow[{}]{a|a^{\prime }}\overline{s^{\prime }}$
and
$s\xrightarrow[{}]{a|a^{\prime }}\overline{s^{\prime }}$
and
 $\overline{s}\xrightarrow[{}]{a|a^{\prime }}s^{\prime }$
.
$\overline{s}\xrightarrow[{}]{a|a^{\prime }}s^{\prime }$
.
The resulting automaton then has 12 states. It is also a GIFS for the boundary, but each boundary part
![]() $K_{s}$
is duplicated (
$K_{s}$
is duplicated (
![]() $K_{s}=K_{\overline{s}}$
). This automaton can be ordered as in Figure 5 to perform the boundary parametrization. We denote by
$K_{s}=K_{\overline{s}}$
). This automaton can be ordered as in Figure 5 to perform the boundary parametrization. We denote by
![]() $R:=\{1,2,\ldots ,\overline{5},\overline{6}\}$
the set of states of this ordered extension
$R:=\{1,2,\ldots ,\overline{5},\overline{6}\}$
the set of states of this ordered extension
![]() $G({\mathcal{R}})^{o}$
. It follows that
$G({\mathcal{R}})^{o}$
. It follows that
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
satisfies
$\unicode[STIX]{x2202}{\mathcal{T}}$
satisfies
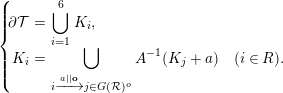 $$\begin{eqnarray}\left\{\!\!\!\begin{array}{@{}rcl@{}}\unicode[STIX]{x2202}{\mathcal{T}}\ & =\ & \displaystyle \mathop{\bigcup }_{i=1}^{6}K_{i},\\ K_{i}\ & =\ & \displaystyle \mathop{\bigcup }_{i\xrightarrow[{}]{a||\mathbf{o}}j\in G({\mathcal{R}})^{o}}A^{-1}(K_{j}+a)\quad (i\in R).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\!\!\!\begin{array}{@{}rcl@{}}\unicode[STIX]{x2202}{\mathcal{T}}\ & =\ & \displaystyle \mathop{\bigcup }_{i=1}^{6}K_{i},\\ K_{i}\ & =\ & \displaystyle \mathop{\bigcup }_{i\xrightarrow[{}]{a||\mathbf{o}}j\in G({\mathcal{R}})^{o}}A^{-1}(K_{j}+a)\quad (i\in R).\end{array}\right.\end{eqnarray}$$
Note that

Figure 5. Ordered extension
![]() $G({\mathcal{R}})^{o}$
for the example of Bandt and Gelbrich.
$G({\mathcal{R}})^{o}$
for the example of Bandt and Gelbrich.
The following theorem justifies Assumptions 1 and 2.
Theorem 4. Let
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
be the self-affine tile associated to the data (6.1). Let
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
be the self-affine tile associated to the data (6.1). Let
![]() $\unicode[STIX]{x1D6FD}:=\frac{1+\sqrt{13}}{2}$
. Then, there exist a
$\unicode[STIX]{x1D6FD}:=\frac{1+\sqrt{13}}{2}$
. Then, there exist a
![]() $C:[0,1]\rightarrow \unicode[STIX]{x2202}{\mathcal{T}}$
Hölder continuous onto mapping with
$C:[0,1]\rightarrow \unicode[STIX]{x2202}{\mathcal{T}}$
Hölder continuous onto mapping with
![]() $C(0)=C(1)$
and a hexagon
$C(0)=C(1)$
and a hexagon
![]() $Q\subset \mathbb{R}^{2}$
with the following properties. Let
$Q\subset \mathbb{R}^{2}$
with the following properties. Let
![]() $({\mathcal{T}}_{n})_{n\geqslant 0}$
be the sequence of approximations of
$({\mathcal{T}}_{n})_{n\geqslant 0}$
be the sequence of approximations of
![]() ${\mathcal{T}}$
associated to
${\mathcal{T}}$
associated to
![]() $Q$
; that is,
$Q$
; that is,
![]() ${\mathcal{T}}_{0}:=Q$
and, for
${\mathcal{T}}_{0}:=Q$
and, for
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
![]() ${\mathcal{T}}_{n}$
is defined by
${\mathcal{T}}_{n}$
is defined by
Then, we have the following.
-
(1)
 $\lim _{n\rightarrow \infty }{\mathcal{T}}_{n}={\mathcal{T}}$
and
$\lim _{n\rightarrow \infty }{\mathcal{T}}_{n}={\mathcal{T}}$
and
 $\lim _{n\rightarrow \infty }\unicode[STIX]{x2202}{\mathcal{T}}_{n}=\unicode[STIX]{x2202}{\mathcal{T}}$
(in Hausdorff metric).
$\lim _{n\rightarrow \infty }\unicode[STIX]{x2202}{\mathcal{T}}_{n}=\unicode[STIX]{x2202}{\mathcal{T}}$
(in Hausdorff metric). -
(2) Denote by
 $V_{n}$
the set of vertices of
$V_{n}$
the set of vertices of
 $\unicode[STIX]{x2202}{\mathcal{T}}_{n}$
. For all
$\unicode[STIX]{x2202}{\mathcal{T}}_{n}$
. For all
 $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
 $V_{n}\subset V_{n+1}\subset C(\mathbb{Q}(\unicode[STIX]{x1D6FD})\cap [0,1])$
(i.e., the vertices have
$V_{n}\subset V_{n+1}\subset C(\mathbb{Q}(\unicode[STIX]{x1D6FD})\cap [0,1])$
(i.e., the vertices have
 $\mathbb{Q}(\unicode[STIX]{x1D6FD})$
-addresses in the parametrization).
$\mathbb{Q}(\unicode[STIX]{x1D6FD})$
-addresses in the parametrization). -
(3) For all
 $n\geqslant 0$
,
$n\geqslant 0$
,
 $\unicode[STIX]{x2202}{\mathcal{T}}_{n}$
is a simple closed curve.
$\unicode[STIX]{x2202}{\mathcal{T}}_{n}$
is a simple closed curve.
Proof.
![]() $G({\mathcal{R}})^{o}$
is the union of two strongly connected components. Each component has the same irreducible incidence matrix
$G({\mathcal{R}})^{o}$
is the union of two strongly connected components. Each component has the same irreducible incidence matrix
![]() $\mathbf{C}$
, whose Perron–Frobenius eigenvalue
$\mathbf{C}$
, whose Perron–Frobenius eigenvalue
![]() $\unicode[STIX]{x1D6FD}=\frac{1+\sqrt{13}}{2}$
is the largest root of the characteristic polynomial
$\unicode[STIX]{x1D6FD}=\frac{1+\sqrt{13}}{2}$
is the largest root of the characteristic polynomial
![]() $x^{6}-8x^{4}+16x^{2}-9$
. Therefore, the incidence matrix
$x^{6}-8x^{4}+16x^{2}-9$
. Therefore, the incidence matrix
![]() $\mathbf{D}$
of
$\mathbf{D}$
of
![]() $G({\mathcal{R}})^{o}$
has a strictly positive left eigenvector
$G({\mathcal{R}})^{o}$
has a strictly positive left eigenvector
![]() $\mathbf{u}=(u_{1},\ldots ,u_{6},u_{\overline{1}},\ldots ,u_{\overline{6}})$
associated to
$\mathbf{u}=(u_{1},\ldots ,u_{6},u_{\overline{1}},\ldots ,u_{\overline{6}})$
associated to
![]() $\unicode[STIX]{x1D6FD}$
, which can be chosen such that
$\unicode[STIX]{x1D6FD}$
, which can be chosen such that
![]() $u_{1}+\cdots +u_{6}=1$
. This is sufficient to perform the parametrization procedure (see [Reference Akiyama and LoridantAL10] for more details). We just need to check the compatibility conditions of Definition 2.3 with
$u_{1}+\cdots +u_{6}=1$
. This is sufficient to perform the parametrization procedure (see [Reference Akiyama and LoridantAL10] for more details). We just need to check the compatibility conditions of Definition 2.3 with
![]() $p=12$
, together with the additional compatibility condition
$p=12$
, together with the additional compatibility condition
Here,
![]() $\unicode[STIX]{x1D713}$
is naturally defined as in Section 2. All of these compatibility conditions consist of showing that pairs of digit sequences
$\unicode[STIX]{x1D713}$
is naturally defined as in Section 2. All of these compatibility conditions consist of showing that pairs of digit sequences
![]() $(a_{n})_{n\geqslant 1}$
and
$(a_{n})_{n\geqslant 1}$
and
![]() $(a_{n}^{\prime })_{n\geqslant 1}$
lead to the same boundary point; that is,
$(a_{n}^{\prime })_{n\geqslant 1}$
lead to the same boundary point; that is,
This can be checked on the automata depicted in Figures 7 and 8. We refer to Proposition 6.3 for the construction of these automata. Applying Theorem 2.4, we obtain the existence of the Hölder parametrization
![]() $C:[0,1]\rightarrow \unicode[STIX]{x2202}T$
with
$C:[0,1]\rightarrow \unicode[STIX]{x2202}T$
with
![]() $C(0)=C(1)$
.
$C(0)=C(1)$
.
The hexagon
![]() $Q$
is defined in Proposition 6.1 and depicted in Figure 10. The first part of Item (1) is then just the consequence that
$Q$
is defined in Proposition 6.1 and depicted in Figure 10. The first part of Item (1) is then just the consequence that
![]() ${\mathcal{T}}$
is the attractor of the iterated function system (IFS)
${\mathcal{T}}$
is the attractor of the iterated function system (IFS)
![]() $\{x\mapsto A^{-1}(x+a)\}_{a\in {\mathcal{D}}}$
.
$\{x\mapsto A^{-1}(x+a)\}_{a\in {\mathcal{D}}}$
.
The second part of Item (1) as well as Item (2) can be proved as in [Reference Akiyama and LoridantAL11, Proposition 5.7]. This consists of showing for all
![]() $n\geqslant 0$
that
$n\geqslant 0$
that
![]() $\unicode[STIX]{x2202}{\mathcal{T}}_{n}$
is equal to
$\unicode[STIX]{x2202}{\mathcal{T}}_{n}$
is equal to
![]() $\unicode[STIX]{x1D6E5}_{n}$
, the sequence of boundary approximations given by Theorem 2.4.
$\unicode[STIX]{x1D6E5}_{n}$
, the sequence of boundary approximations given by Theorem 2.4.
Item (3) can be proved similarly to [Reference Akiyama and LoridantAL11, Proposition 5.6]. The proof relies on the fact that the hexagon
![]() $Q$
induces a tiling by its translations in which the neighboring tiles have a one-dimensional intersection (see Proposition 6.1 and Figure 10). One then uses the property that
$Q$
induces a tiling by its translations in which the neighboring tiles have a one-dimensional intersection (see Proposition 6.1 and Figure 10). One then uses the property that
![]() $A^{n}{\mathcal{T}}_{n}$
is a connected union of translations of the hexagon
$A^{n}{\mathcal{T}}_{n}$
is a connected union of translations of the hexagon
![]() $Q$
and has therefore, as well as
$Q$
and has therefore, as well as
![]() ${\mathcal{T}}_{n}$
, a connected interior.◻
${\mathcal{T}}_{n}$
, a connected interior.◻
Proposition 6.1. For
![]() $i\in \{1,2,3,4,5,6\}$
, let
$i\in \{1,2,3,4,5,6\}$
, let
![]() $C_{i}:=\unicode[STIX]{x1D713}(i;\overline{\mathbf{1}})$
, and let
$C_{i}:=\unicode[STIX]{x1D713}(i;\overline{\mathbf{1}})$
, and let
![]() $[C_{1},\ldots ,C_{6},C_{1}]$
be the polygonal curve obtained by joining the points
$[C_{1},\ldots ,C_{6},C_{1}]$
be the polygonal curve obtained by joining the points
![]() $C_{1},\ldots ,C_{6},C_{1}$
in this order. Then,
$C_{1},\ldots ,C_{6},C_{1}$
in this order. Then,
![]() $[C_{1},\ldots ,C_{6},C_{1}]$
is a simple closed curve. Let
$[C_{1},\ldots ,C_{6},C_{1}]$
is a simple closed curve. Let
![]() $Q$
be the closure of its bounded complementary component. Then,
$Q$
be the closure of its bounded complementary component. Then,
![]() $Q$
tiles
$Q$
tiles
![]() $\mathbb{R}^{2}$
by
$\mathbb{R}^{2}$
by
![]() $\mathbb{Z}^{2}$
. Moreover, the neighbors of
$\mathbb{Z}^{2}$
. Moreover, the neighbors of
![]() $Q$
in this tiling are the tiles
$Q$
in this tiling are the tiles
![]() $Q+s$
with
$Q+s$
with
![]() $s\in {\mathcal{R}}$
, and
$s\in {\mathcal{R}}$
, and
Proof. We compute
Joining the points
![]() $C_{1},C_{2},\ldots ,C_{6},C_{1}$
in this order yields a simple closed curve. The closure of the bounded component of its complement in
$C_{1},C_{2},\ldots ,C_{6},C_{1}$
in this order yields a simple closed curve. The closure of the bounded component of its complement in
![]() $\mathbb{R}^{2}$
is a hexagon
$\mathbb{R}^{2}$
is a hexagon
![]() $Q$
depicted in Figure 10. Consider the quadrilateral
$Q$
depicted in Figure 10. Consider the quadrilateral
![]() $H_{1}$
with vertices
$H_{1}$
with vertices
![]() $C_{6},C_{1},C_{2},C_{3}$
and the quadrilateral
$C_{6},C_{1},C_{2},C_{3}$
and the quadrilateral
![]() $H_{2}$
with vertices
$H_{2}$
with vertices
![]() $C_{3},C_{4},C_{5},C_{6}$
. Then
$C_{3},C_{4},C_{5},C_{6}$
. Then
![]() $H_{1}\cup (H_{2}+(-1,1))$
is a parallelogram which obviously tiles the plane by
$H_{1}\cup (H_{2}+(-1,1))$
is a parallelogram which obviously tiles the plane by
![]() $\mathbb{Z}^{2}$
. It follows that
$\mathbb{Z}^{2}$
. It follows that
![]() $Q$
itself tiles the plane by
$Q$
itself tiles the plane by
![]() $\mathbb{Z}^{2}$
.◻
$\mathbb{Z}^{2}$
.◻
As mentioned in the proof of Theorem 4, checking the compatibility conditions
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
in Definition 2.3 amounts to proving equalities of the form
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
in Definition 2.3 amounts to proving equalities of the form
![]() $\sum _{n\geqslant 1}A^{-n}a_{n}=\sum _{n\geqslant 1}A^{-n}a_{n}^{\prime }$
for sequences of digits
$\sum _{n\geqslant 1}A^{-n}a_{n}=\sum _{n\geqslant 1}A^{-n}a_{n}^{\prime }$
for sequences of digits
![]() $(a_{n}),(a_{n}^{\prime })$
. Moreover, for topological purposes, we look for all pairs of parameters
$(a_{n}),(a_{n}^{\prime })$
. Moreover, for topological purposes, we look for all pairs of parameters
![]() $(t,t^{\prime })$
with
$(t,t^{\prime })$
with
![]() $t\neq t^{\prime }\in [0,1)$
fulfilling
$t\neq t^{\prime }\in [0,1)$
fulfilling
![]() $C(t)=C(t^{\prime })$
(noninjectivity points). This requires us to find all pairs
$C(t)=C(t^{\prime })$
(noninjectivity points). This requires us to find all pairs
![]() $(w,w^{\prime })$
of walks
$(w,w^{\prime })$
of walks
![]() $w,w^{\prime }\in G({\mathcal{R}})^{o}$
satisfying
$w,w^{\prime }\in G({\mathcal{R}})^{o}$
satisfying
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
other than the pairs
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
other than the pairs
![]() $(w,w^{\prime })$
of walks considered in the compatibility conditions. The right context for these computations is the framework of Büchi automata.
$(w,w^{\prime })$
of walks considered in the compatibility conditions. The right context for these computations is the framework of Büchi automata.
Definition 6.2. Let
![]() ${\mathcal{A}}=(S,\unicode[STIX]{x1D6EC},E)$
be an automaton; that is,
${\mathcal{A}}=(S,\unicode[STIX]{x1D6EC},E)$
be an automaton; that is,
![]() $S$
is a finite set of states,
$S$
is a finite set of states,
![]() $\unicode[STIX]{x1D6EC}$
is a finite set of labels and
$\unicode[STIX]{x1D6EC}$
is a finite set of labels and
![]() $E\subset S\times \unicode[STIX]{x1D6EC}\times S$
is the set of transitions. Note that for
$E\subset S\times \unicode[STIX]{x1D6EC}\times S$
is the set of transitions. Note that for
![]() $(t,l,t^{\prime })\in E$
, we usually write
$(t,l,t^{\prime })\in E$
, we usually write
![]() $t\xrightarrow[{}]{l}t^{\prime }$
. Let
$t\xrightarrow[{}]{l}t^{\prime }$
. Let
![]() $I,F\subset S$
. Then,
$I,F\subset S$
. Then,
![]() $(S,\unicode[STIX]{x1D6EC},E,I,F)$
is called a Büchi automaton with the set of initial states
$(S,\unicode[STIX]{x1D6EC},E,I,F)$
is called a Büchi automaton with the set of initial states
![]() $I$
and the set of final states
$I$
and the set of final states
![]() $F$
. An infinite walk
$F$
. An infinite walk
in the automaton
![]() ${\mathcal{A}}$
is called admissible if it starts from a state of
${\mathcal{A}}$
is called admissible if it starts from a state of
![]() $I$
(
$I$
(
![]() $t_{1}\in I$
) and visits
$t_{1}\in I$
) and visits
![]() $F$
infinitely often. (This means that
$F$
infinitely often. (This means that
![]() $\{t_{n};n\geqslant 1\}\cap F$
is infinite.)
$\{t_{n};n\geqslant 1\}\cap F$
is infinite.)
A Büchi automaton
![]() ${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
collects all pairs
${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
collects all pairs
![]() $(w,w^{\prime })$
of distinct walks
$(w,w^{\prime })$
of distinct walks
![]() $w,w^{\prime }$
in
$w,w^{\prime }$
in
![]() $G({\mathcal{S}})$
(Figure 4) whose sequences of labels
$G({\mathcal{S}})$
(Figure 4) whose sequences of labels
![]() $(a_{n}),(a_{n}^{\prime })$
fulfill
$(a_{n}),(a_{n}^{\prime })$
fulfill
![]() $\sum _{n\geqslant 1}A^{-n}a_{n}=\sum _{n\geqslant 1}A^{-n}a_{n}^{\prime }$
(Figure 6). To infer from this automaton the pairs of parameters
$\sum _{n\geqslant 1}A^{-n}a_{n}=\sum _{n\geqslant 1}A^{-n}a_{n}^{\prime }$
(Figure 6). To infer from this automaton the pairs of parameters
![]() $(t,t^{\prime })$
satisfying
$(t,t^{\prime })$
satisfying
![]() $t\neq t^{\prime }$
and
$t\neq t^{\prime }$
and
![]() $C(t)=C(t^{\prime })$
, we transfer it to Büchi automata built up from
$C(t)=C(t^{\prime })$
, we transfer it to Büchi automata built up from
![]() $G({\mathcal{R}})^{o}$
. A Büchi automaton
$G({\mathcal{R}})^{o}$
. A Büchi automaton
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
collects all pairs
${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
collects all pairs
![]() $(w,w^{\prime })$
of distinct walks
$(w,w^{\prime })$
of distinct walks
![]() $w,w^{\prime }\in G({\mathcal{R}})^{o}$
satisfying
$w,w^{\prime }\in G({\mathcal{R}})^{o}$
satisfying
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
and corresponding to different sequences of digits
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
and corresponding to different sequences of digits
![]() $(a_{n}),(a_{n}^{\prime })$
(Figure 7). Another Büchi automaton
$(a_{n}),(a_{n}^{\prime })$
(Figure 7). Another Büchi automaton
![]() ${\mathcal{A}}^{sl}$
collects all pairs
${\mathcal{A}}^{sl}$
collects all pairs
![]() $(w,w^{\prime })$
of distinct walks
$(w,w^{\prime })$
of distinct walks
![]() $w,w^{\prime }\in G({\mathcal{R}})^{o}$
satisfying
$w,w^{\prime }\in G({\mathcal{R}})^{o}$
satisfying
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
and corresponding to the same sequence of digits
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
and corresponding to the same sequence of digits
![]() $(a_{n}),(a_{n}^{\prime })=(a_{n})$
(Figure 8). Erasing from
$(a_{n}),(a_{n}^{\prime })=(a_{n})$
(Figure 8). Erasing from
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D713}}\cup {\mathcal{A}}^{sl}$
the pairs of walks
${\mathcal{A}}^{\unicode[STIX]{x1D713}}\cup {\mathcal{A}}^{sl}$
the pairs of walks
![]() $(w,w^{\prime })$
corresponding to the compatibility conditions (Definition 2.3), we obtain the desired pairs of walks associated with all pairs of parameters
$(w,w^{\prime })$
corresponding to the compatibility conditions (Definition 2.3), we obtain the desired pairs of walks associated with all pairs of parameters
![]() $(t,t^{\prime })$
with
$(t,t^{\prime })$
with
![]() $t\neq t^{\prime }\in [0,1)$
and fulfilling
$t\neq t^{\prime }\in [0,1)$
and fulfilling
![]() $C(t)=C(t^{\prime })$
. This operation of “erasing” is related to the so-called complementation of Büchi automata, which can be a difficult task in general. However, it turns out to be easy in our example (see Definition 6.4, Proposition 6.5 and the paragraph between them).
$C(t)=C(t^{\prime })$
. This operation of “erasing” is related to the so-called complementation of Büchi automata, which can be a difficult task in general. However, it turns out to be easy in our example (see Definition 6.4, Proposition 6.5 and the paragraph between them).

Figure 6. Example of Bandt and Gelbrich: automaton
![]() ${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
.
${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
.

Figure 7. Example of Bandt and Gelbrich: automaton
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
.
${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
.

Figure 8. Example of Bandt and Gelbrich: automaton
![]() ${\mathcal{A}}^{sl}$
.
${\mathcal{A}}^{sl}$
.
Proposition 6.3. Let
![]() $w\neq w^{\prime }$
infinite walks in
$w\neq w^{\prime }$
infinite walks in
![]() $G({\mathcal{R}})^{o}$
with
$G({\mathcal{R}})^{o}$
with
and
where
![]() $i,j\in \{1,2,3,4,5,6\}$
. Then,
$i,j\in \{1,2,3,4,5,6\}$
. Then,
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
if and only if, up to permutation of
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
if and only if, up to permutation of
![]() $w$
and
$w$
and
![]() $w^{\prime }$
, one of the following holds.
$w^{\prime }$
, one of the following holds.
-
∙
 $i=j$
and (6.5)is an admissible walk in
$i=j$
and (6.5)is an admissible walk in $$\begin{eqnarray}i|i\xrightarrow[{}]{\mathbf{o}_{\mathbf{1}}||\mathbf{o}_{\mathbf{1}}^{\prime }}\cdots\end{eqnarray}$$
$$\begin{eqnarray}i|i\xrightarrow[{}]{\mathbf{o}_{\mathbf{1}}||\mathbf{o}_{\mathbf{1}}^{\prime }}\cdots\end{eqnarray}$$
 ${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
depicted in Figure 7.
${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
depicted in Figure 7.
-
∙ The walk
(6.6)is an admissible walk in $$\begin{eqnarray}i|j\xrightarrow[{}]{\mathbf{o}_{\mathbf{1}}||\mathbf{o}_{\mathbf{1}}^{\prime }}\cdots\end{eqnarray}$$
$$\begin{eqnarray}i|j\xrightarrow[{}]{\mathbf{o}_{\mathbf{1}}||\mathbf{o}_{\mathbf{1}}^{\prime }}\cdots\end{eqnarray}$$
 ${\mathcal{A}}^{sl}$
depicted in Figure 8.
${\mathcal{A}}^{sl}$
depicted in Figure 8.
In both automata, the gray states are the initial states and the double lined states are the final states.
Proof. By definition,
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })\;\Longleftrightarrow \;\sum _{n\geqslant 1}A^{-n}a_{n}=\sum _{n\geqslant 1}A^{-n}a_{n}^{\prime }$
. This point must belong to a boundary part
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })\;\Longleftrightarrow \;\sum _{n\geqslant 1}A^{-n}a_{n}=\sum _{n\geqslant 1}A^{-n}a_{n}^{\prime }$
. This point must belong to a boundary part
![]() $K_{s_{0}}$
for some
$K_{s_{0}}$
for some
![]() $s_{0}\in {\mathcal{R}}$
. Suppose that the digit labels
$s_{0}\in {\mathcal{R}}$
. Suppose that the digit labels
![]() $(a_{n})_{n\geqslant 1}$
and
$(a_{n})_{n\geqslant 1}$
and
![]() $(a_{n}^{\prime })_{n\geqslant 1}$
are distinct, and let
$(a_{n}^{\prime })_{n\geqslant 1}$
are distinct, and let
![]() $m\geqslant 0$
be the least integer such that
$m\geqslant 0$
be the least integer such that
![]() $a_{m+1}\neq a_{m+1}^{\prime }$
. By Proposition 2.1, there must be
$a_{m+1}\neq a_{m+1}^{\prime }$
. By Proposition 2.1, there must be
![]() $(a_{n}^{\prime \prime })_{n\geqslant 1}\in {\mathcal{D}}^{\mathbb{N}}$
and walks
$(a_{n}^{\prime \prime })_{n\geqslant 1}\in {\mathcal{D}}^{\mathbb{N}}$
and walks
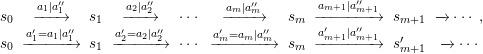 $$\begin{eqnarray}\begin{array}{@{}cccccccccc@{}}s_{0}~\, & \xrightarrow[{}]{a_{1}|a_{1}^{\prime \prime }}~\, & s_{1}~\, & \xrightarrow[{}]{a_{2}|a_{2}^{\prime \prime }}~\, & \cdots \,~\, & \xrightarrow[{}]{a_{m}|a_{m}^{\prime \prime }}~\, & s_{m}~\, & \xrightarrow[{}]{a_{m+1}|a_{m+1}^{\prime \prime }}~\, & s_{m+1}~\, & \xrightarrow[{}]{}\cdots \,,\\ s_{0}~\, & \xrightarrow[{}]{a_{1}^{\prime }=a_{1}|a_{1}^{\prime \prime }}~\, & s_{1}~\, & \xrightarrow[{}]{a_{2}^{\prime }=a_{2}|a_{2}^{\prime \prime }}~\, & \cdots \,~\, & \xrightarrow[{}]{a_{m}^{\prime }=a_{m}|a_{m}^{\prime \prime }}~\, & s_{m}~\, & \xrightarrow[{}]{a_{m+1}^{\prime }|a_{m+1}^{\prime \prime }}~\, & s_{m+1}^{\prime }~\, & \xrightarrow[{}]{}\cdots \end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cccccccccc@{}}s_{0}~\, & \xrightarrow[{}]{a_{1}|a_{1}^{\prime \prime }}~\, & s_{1}~\, & \xrightarrow[{}]{a_{2}|a_{2}^{\prime \prime }}~\, & \cdots \,~\, & \xrightarrow[{}]{a_{m}|a_{m}^{\prime \prime }}~\, & s_{m}~\, & \xrightarrow[{}]{a_{m+1}|a_{m+1}^{\prime \prime }}~\, & s_{m+1}~\, & \xrightarrow[{}]{}\cdots \,,\\ s_{0}~\, & \xrightarrow[{}]{a_{1}^{\prime }=a_{1}|a_{1}^{\prime \prime }}~\, & s_{1}~\, & \xrightarrow[{}]{a_{2}^{\prime }=a_{2}|a_{2}^{\prime \prime }}~\, & \cdots \,~\, & \xrightarrow[{}]{a_{m}^{\prime }=a_{m}|a_{m}^{\prime \prime }}~\, & s_{m}~\, & \xrightarrow[{}]{a_{m+1}^{\prime }|a_{m+1}^{\prime \prime }}~\, & s_{m+1}^{\prime }~\, & \xrightarrow[{}]{}\cdots \end{array}\end{eqnarray}$$
in
![]() $G({\mathcal{S}})$
. As proved in [Reference Akiyama and LoridantAL11, Section 4], these pairs of walks are recognized as the admissible walks of a Büchi automaton
$G({\mathcal{S}})$
. As proved in [Reference Akiyama and LoridantAL11, Section 4], these pairs of walks are recognized as the admissible walks of a Büchi automaton
![]() ${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
, depicted in Figure 6.
${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
, depicted in Figure 6.
Note that some pairs of walks
![]() $(w,w^{\prime })$
recognized by
$(w,w^{\prime })$
recognized by
![]() ${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
satisfy
${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
satisfy
![]() $w^{\prime }\in {\mathcal{G}}({\mathcal{S}})\setminus {\mathcal{G}}({\mathcal{R}})$
. However, it is easy to check that the corresponding digit sequence
$w^{\prime }\in {\mathcal{G}}({\mathcal{S}})\setminus {\mathcal{G}}({\mathcal{R}})$
. However, it is easy to check that the corresponding digit sequence
![]() $(a_{n}^{\prime })_{n\geqslant 1}$
of such a
$(a_{n}^{\prime })_{n\geqslant 1}$
of such a
![]() $w^{\prime }$
does not appear as a digit sequence of any other walk of
$w^{\prime }$
does not appear as a digit sequence of any other walk of
![]() $G({\mathcal{S}})$
. We therefore delete these pairs of walks from
$G({\mathcal{S}})$
. We therefore delete these pairs of walks from
![]() ${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
and obtain the automaton
${\mathcal{I}}^{\unicode[STIX]{x1D713}}$
and obtain the automaton
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
of Figure 7. In this figure, we use for the states and edges the elements of the ordered extension
${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
of Figure 7. In this figure, we use for the states and edges the elements of the ordered extension
![]() $G({\mathcal{R}})^{o}$
. Pairs of infinite walks
$G({\mathcal{R}})^{o}$
. Pairs of infinite walks
![]() $(w,w^{\prime })$
,
$(w,w^{\prime })$
,
![]() $w\neq w^{\prime }$
in
$w\neq w^{\prime }$
in
![]() $G({\mathcal{R}})^{o}$
both starting in
$G({\mathcal{R}})^{o}$
both starting in
![]() $\{1,2,3,4,5,6\}$
, having distinct digit sequences
$\{1,2,3,4,5,6\}$
, having distinct digit sequences
![]() $(a_{n})_{n\geqslant 1}\neq (a_{n}^{\prime })_{n\geqslant 1}$
and satisfying
$(a_{n})_{n\geqslant 1}\neq (a_{n}^{\prime })_{n\geqslant 1}$
and satisfying
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
, are of the form (6.5).
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
, are of the form (6.5).
For
![]() $w\neq w^{\prime }$
infinite walks in
$w\neq w^{\prime }$
infinite walks in
![]() $G({\mathcal{R}})^{o}$
with
$G({\mathcal{R}})^{o}$
with
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
and identical digit sequences
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
and identical digit sequences
![]() $(a_{n})_{n\geqslant 1}=(a_{n}^{\prime })_{n\geqslant 1}$
, we construct the automaton
$(a_{n})_{n\geqslant 1}=(a_{n}^{\prime })_{n\geqslant 1}$
, we construct the automaton
![]() ${\mathcal{A}}^{sl}$
as in [Reference Akiyama and LoridantAL11] and depict it in Figure 8.◻
${\mathcal{A}}^{sl}$
as in [Reference Akiyama and LoridantAL11] and depict it in Figure 8.◻
The pairs
![]() $(w,w^{\prime })$
of walks
$(w,w^{\prime })$
of walks
![]() $w,w^{\prime }\in G({\mathcal{R}})^{o}$
associated to the compatibility conditions (Definition 2.3) are called trivial identifications, according to the following definition.
$w,w^{\prime }\in G({\mathcal{R}})^{o}$
associated to the compatibility conditions (Definition 2.3) are called trivial identifications, according to the following definition.
Definition 6.4. Let
![]() $w\neq w^{\prime }$
be two walks of
$w\neq w^{\prime }$
be two walks of
![]() $G({\mathcal{R}})^{o}$
starting in
$G({\mathcal{R}})^{o}$
starting in
![]() $\{1,2,3,4,5,6\}$
and satisfying the equality
$\{1,2,3,4,5,6\}$
and satisfying the equality
![]() $\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
. We call the pair
$\unicode[STIX]{x1D713}(w)=\unicode[STIX]{x1D713}(w^{\prime })$
. We call the pair
![]() $(w,w^{\prime })$
trivial identification (in the Dumont–Thomas number system) if, up to permutation of
$(w,w^{\prime })$
trivial identification (in the Dumont–Thomas number system) if, up to permutation of
![]() $w$
and
$w$
and
![]() $w^{\prime }$
, there is a walk
$w^{\prime }$
, there is a walk
![]() $w_{0}$
of length
$w_{0}$
of length
![]() $n$
in
$n$
in
![]() $G({\mathcal{R}})^{o}$
such that
$G({\mathcal{R}})^{o}$
such that
Here,
![]() $w_{0}^{+}$
is the next walk of length
$w_{0}^{+}$
is the next walk of length
![]() $n$
in lexicographical order in
$n$
in lexicographical order in
![]() $G({\mathcal{R}})^{o}$
. By convention,
$G({\mathcal{R}})^{o}$
. By convention,
By definition, the walks of a trivial identification are associated to the same parameter
![]() $t\in [0,1]$
in our parametrization. On the contrary, nontrivial identifications make the parametrization noninjective. Finding out the nontrivial identifications can be a difficult task: it is related to the complementation of Büchi automata. In our example, it is easy to see that
$t\in [0,1]$
in our parametrization. On the contrary, nontrivial identifications make the parametrization noninjective. Finding out the nontrivial identifications can be a difficult task: it is related to the complementation of Büchi automata. In our example, it is easy to see that
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
only gives rise to trivial identifications. Moreover, the identifications in
${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
only gives rise to trivial identifications. Moreover, the identifications in
![]() ${\mathcal{A}}^{sl}$
depicted in the top part of Figure 8 only give rise to trivial identifications. However, in the bottom part, we can find the following nontrivial identifications.
${\mathcal{A}}^{sl}$
depicted in the top part of Figure 8 only give rise to trivial identifications. However, in the bottom part, we can find the following nontrivial identifications.
Proposition 6.5. The pair
![]() $(w,w^{\prime })$
is a nontrivial identification in the Dumont–Thomas number system if and only if it is a pair of Figure 9, up to permutation of
$(w,w^{\prime })$
is a nontrivial identification in the Dumont–Thomas number system if and only if it is a pair of Figure 9, up to permutation of
![]() $w$
and
$w$
and
![]() $w^{\prime }$
. The associated points in
$w^{\prime }$
. The associated points in
![]() $[0,1]$
are schematically represented in Figure 9 too. Here, for
$[0,1]$
are schematically represented in Figure 9 too. Here, for
![]() $i\in \{1,\ldots ,6\}$
, the circled number
$i\in \{1,\ldots ,6\}$
, the circled number ![]() stands for the parameter of
stands for the parameter of
![]() $[0,1]$
associated with the walk
$[0,1]$
associated with the walk
![]() $(i;\overline{\mathbf{1}})$
. No two pairs of identifications are crossing.
$(i;\overline{\mathbf{1}})$
. No two pairs of identifications are crossing.

Figure 9. Nontrivial identifications in the example of Bandt and Gelbrich.
Proof. As mentioned above,
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
and the part of
${\mathcal{A}}^{\unicode[STIX]{x1D713}}$
and the part of
![]() ${\mathcal{A}}^{sl}$
at the top of Figure 8 only give rise to trivial identifications. In the bottom part, we find the trivial identifications
${\mathcal{A}}^{sl}$
at the top of Figure 8 only give rise to trivial identifications. In the bottom part, we find the trivial identifications
The other identifications are nontrivial and are listed in Figure 9. ◻
This allows us to determine all of the cut points of
![]() ${\mathcal{T}}$
. These are the points
${\mathcal{T}}$
. These are the points
![]() $z\in {\mathcal{T}}$
such that
$z\in {\mathcal{T}}$
such that
![]() ${\mathcal{T}}\setminus \{z\}$
is no more connected.
${\mathcal{T}}\setminus \{z\}$
is no more connected.
Theorem 5. Let
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
be the tile associated to the data (6.1). For
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
be the tile associated to the data (6.1). For
![]() $i\in \{0,1,-1\}$
, we denote by
$i\in \{0,1,-1\}$
, we denote by
![]() $f_{i}(x)=A^{-1}(x+(i,0)^{T})$
the corresponding contraction. Then, the sequence of cut points of
$f_{i}(x)=A^{-1}(x+(i,0)^{T})$
the corresponding contraction. Then, the sequence of cut points of
![]() ${\mathcal{T}}$
reads as follows (
${\mathcal{T}}$
reads as follows (
![]() $n\geqslant 0$
):
$n\geqslant 0$
):
-
(i)
 $f_{1}^{2n+2}((0,0)^{T})$
;
$f_{1}^{2n+2}((0,0)^{T})$
; -
(ii)
 $f_{1}^{2n+3}((0,0)^{T})$
;
$f_{1}^{2n+3}((0,0)^{T})$
; -
(iii)
 $f_{1}((0,0)^{T})$
;
$f_{1}((0,0)^{T})$
; -
(iv)
 $(0,0)^{T}$
;
$(0,0)^{T}$
; -
(v)
 $f_{-1}^{2n+2}((0,0)^{T})$
;
$f_{-1}^{2n+2}((0,0)^{T})$
; -
(vi)
 $f_{-1}^{2n+3}((0,0)^{T})$
;
$f_{-1}^{2n+3}((0,0)^{T})$
; -
(vii)
 $f_{-1}((0,0)^{T})$
.
$f_{-1}((0,0)^{T})$
.
Proof. We show that each cut point corresponds to a nontrivial identification listed in Figure 9.

Figure 10. Example of Bandt and Gelbrich: hexagon
![]() $Q$
and associated tiling.
$Q$
and associated tiling.
First, note that for every
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
![]() $C([0,1]\setminus \{t\})$
remains connected. (Remember that
$C([0,1]\setminus \{t\})$
remains connected. (Remember that
![]() $C(0)=C(1)$
.)
$C(0)=C(1)$
.)
Then, consider, for example, the identification
![]() $(R,R^{\prime })$
and the associated values
$(R,R^{\prime })$
and the associated values
![]() $0<t_{R}<t_{R^{\prime }}<1$
. Denote
$0<t_{R}<t_{R^{\prime }}<1$
. Denote
![]() $z:=C(t_{R})=C(t_{R^{\prime }})$
. Then,
$z:=C(t_{R})=C(t_{R^{\prime }})$
. Then,
![]() $C([0,1]\setminus \{t_{R},t_{R^{\prime }}\})=\unicode[STIX]{x2202}T\setminus \{z\}$
is no more connected: it consists of exactly two connected components, namely
$C([0,1]\setminus \{t_{R},t_{R^{\prime }}\})=\unicode[STIX]{x2202}T\setminus \{z\}$
is no more connected: it consists of exactly two connected components, namely
![]() $C([0,t_{R})\cup (t_{R^{\prime }},1])$
and
$C([0,t_{R})\cup (t_{R^{\prime }},1])$
and
![]() $C((t_{R},t_{R^{\prime }}))$
.
$C((t_{R},t_{R^{\prime }}))$
.
The corresponding sequence of digits is read off from Figure 5:
![]() $P(1;\mathbf{2},\overline{(\mathbf{1},\mathbf{3})})$
is labeled by the sequence of digits
$P(1;\mathbf{2},\overline{(\mathbf{1},\mathbf{3})})$
is labeled by the sequence of digits
![]() $1\overline{00}$
, which is the point
$1\overline{00}$
, which is the point
![]() $f_{1}(\text{Fix}(f_{0}))=(-1/3,1/3)$
, as
$f_{1}(\text{Fix}(f_{0}))=(-1/3,1/3)$
, as
![]() $\text{Fix}(f_{0})=(0,0)^{T}$
. This corresponds to Item (iii) of the theorem.
$\text{Fix}(f_{0})=(0,0)^{T}$
. This corresponds to Item (iii) of the theorem.
This proof holds for every pair of identified walks of Figure 9. Item (i) corresponds to
![]() $(P_{n},P_{n}^{\prime })$
, Item (ii) corresponds to
$(P_{n},P_{n}^{\prime })$
, Item (ii) corresponds to
![]() $(Q_{n},Q_{n}^{\prime })$
, and so on.◻
$(Q_{n},Q_{n}^{\prime })$
, and so on.◻
Furthermore, we can infer the following topological description of the boundary of
![]() ${\mathcal{T}}$
.
${\mathcal{T}}$
.
Theorem 6. The boundary
![]() $\unicode[STIX]{x2202}{\mathcal{T}}$
of the tile
$\unicode[STIX]{x2202}{\mathcal{T}}$
of the tile
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
associated to the data (6.1) is a countable union of simple closed curves, together with two points. These are
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
associated to the data (6.1) is a countable union of simple closed curves, together with two points. These are
-
∙ the curves
 $C([a,c]\cup [d,b])$
, where
$C([a,c]\cup [d,b])$
, where
 $((a,b),(c,d))$
is any pair of consecutive nontrivial identifications; that is,
$((a,b),(c,d))$
is any pair of consecutive nontrivial identifications; that is,
 $0<a<c<d<b<1$
and there is no identification
$0<a<c<d<b<1$
and there is no identification
 $(e,f)$
satisfying
$(e,f)$
satisfying
 $a<e<c$
and
$a<e<c$
and
 $d<f<b$
(see Figure 9);
$d<f<b$
(see Figure 9); -
∙ the curve
 $C([t_{S},1]\cup [0,t_{R}]\cup [t_{R^{\prime }},t_{S^{\prime }}])$
, where
$C([t_{S},1]\cup [0,t_{R}]\cup [t_{R^{\prime }},t_{S^{\prime }}])$
, where
 $t_{S},t_{R},t_{R^{\prime }},t_{S^{\prime }}$
are associated to the walks
$t_{S},t_{R},t_{R^{\prime }},t_{S^{\prime }}$
are associated to the walks
 $S,R,R^{\prime },S^{\prime }$
of Figure 9;
$S,R,R^{\prime },S^{\prime }$
of Figure 9; -
∙ the points
 $\pm (0,1/3)$
.
$\pm (0,1/3)$
.
Each curve intersects exactly two other curves, each at one point.
Proof. This result can be read off from Figure 9. If
![]() $((a,b),(c,d))$
is any pair of consecutive nontrivial identifications satisfying
$((a,b),(c,d))$
is any pair of consecutive nontrivial identifications satisfying
![]() $0<a<c<d<b<1$
, then
$0<a<c<d<b<1$
, then
![]() $C$
is injective on
$C$
is injective on
![]() $[a,c]$
and on
$[a,c]$
and on
![]() $[d,b]$
. Thus,
$[d,b]$
. Thus,
![]() $C([a,c])$
and
$C([a,c])$
and
![]() $C([d,b])$
are two simple arcs meeting only at their extremities
$C([d,b])$
are two simple arcs meeting only at their extremities
![]() $C(a)=C(b)$
and
$C(a)=C(b)$
and
![]() $C(c)=C(d)$
. Their union is therefore a simple closed curve. It meets exactly two other curves, one at
$C(c)=C(d)$
. Their union is therefore a simple closed curve. It meets exactly two other curves, one at
![]() $C(a)=C(b)$
and the other one at
$C(a)=C(b)$
and the other one at
![]() $C(c)=C(d)$
.
$C(c)=C(d)$
.
Similarly,
![]() $C$
is injective on
$C$
is injective on
![]() $[t_{S},1]\cup [0,t_{R}]$
(apart from the trivial identification
$[t_{S},1]\cup [0,t_{R}]$
(apart from the trivial identification
![]() $C(0)=C(1)$
) and on
$C(0)=C(1)$
) and on
![]() $[t_{R^{\prime }},t_{S^{\prime }}]$
. Thus,
$[t_{R^{\prime }},t_{S^{\prime }}]$
. Thus,
![]() $C([t_{S},1]\cup [0,t_{R}])$
and
$C([t_{S},1]\cup [0,t_{R}])$
and
![]() $C([t_{R^{\prime }},t_{S^{\prime }}])$
are two simple arcs meeting only at their extremities
$C([t_{R^{\prime }},t_{S^{\prime }}])$
are two simple arcs meeting only at their extremities
![]() $C(t_{S})=C(t_{S^{\prime }})$
and
$C(t_{S})=C(t_{S^{\prime }})$
and
![]() $C(t_{R})=C(t_{R^{\prime }})$
. Their union is therefore a simple closed curve. It also meets exactly two other curves.
$C(t_{R})=C(t_{R^{\prime }})$
. Their union is therefore a simple closed curve. It also meets exactly two other curves.

Figure 11. Example of Bandt and Gelbrich: boundary approximations.

Figure 12. Example of Bandt and Gelbrich: approximation
![]() $C_{n}(a_{n},b_{n})$
(
$C_{n}(a_{n},b_{n})$
(
![]() $n=2,3,5,6,7,9$
) for
$n=2,3,5,6,7,9$
) for
![]() $(a,b)=(t_{S^{\prime }},t_{S})$
.
$(a,b)=(t_{S^{\prime }},t_{S})$
.

Figure 13. Example of Bandt and Gelbrich: approximation
![]() $D_{n}(a_{n},b_{n})$
(
$D_{n}(a_{n},b_{n})$
(
![]() $n=2,3,5,6,7,9$
) for
$n=2,3,5,6,7,9$
) for
![]() $(a,b)=(t_{S^{\prime }},t_{S})$
.
$(a,b)=(t_{S^{\prime }},t_{S})$
.

Figure 14. Example of Bandt and Gelbrich: approximation
![]() $C_{n}(a_{n},b_{n})\cup D_{n}(a_{n},b_{n})$
(
$C_{n}(a_{n},b_{n})\cup D_{n}(a_{n},b_{n})$
(
![]() $n=2,3,5,6,7,9$
) for
$n=2,3,5,6,7,9$
) for
![]() $(a,b)=(t_{S^{\prime }},t_{S})$
.
$(a,b)=(t_{S^{\prime }},t_{S})$
.

Figure 15. Example of Bandt and Gelbrich: encircling
![]() $C_{n}(a_{n},b_{n})$
(
$C_{n}(a_{n},b_{n})$
(
![]() $n=2,3,4,5,6,7$
) for
$n=2,3,4,5,6,7$
) for
![]() $(a,b)=(t_{S^{\prime }},t_{S})$
.
$(a,b)=(t_{S^{\prime }},t_{S})$
.

Figure 16. Example of Bandt and Gelbrich: encircling
![]() $D_{n}(a_{n},b_{n})$
(
$D_{n}(a_{n},b_{n})$
(
![]() $n=2,3,4,5,6,7$
) for
$n=2,3,4,5,6,7$
) for
![]() $(a,b)=(t_{S^{\prime }},t_{S})$
.
$(a,b)=(t_{S^{\prime }},t_{S})$
.
The point
![]() $(0,1/3)$
corresponds to the infinite walk
$(0,1/3)$
corresponds to the infinite walk
![]() $(2;\overline{\mathbf{1}})$
and the point
$(2;\overline{\mathbf{1}})$
and the point
![]() $(0,-1/3)$
corresponds to the infinite walk
$(0,-1/3)$
corresponds to the infinite walk
![]() $(5;\overline{\mathbf{1}})$
. These are the two accumulation points of the sequence of simple closed curves.
$(5;\overline{\mathbf{1}})$
. These are the two accumulation points of the sequence of simple closed curves.
The union of all these curves together with the two points is equal to
![]() $C([0,1])=\unicode[STIX]{x2202}{\mathcal{T}}$
; hence, the description is complete.◻
$C([0,1])=\unicode[STIX]{x2202}{\mathcal{T}}$
; hence, the description is complete.◻
We now pick up one of these simple closed curves and show that it is the boundary of an interior component.
Theorem 7. Let
![]() $0<t_{S^{\prime }}<t_{V^{\prime }}<t_{V}<t_{S}<1$
be associated to the infinite walks
$0<t_{S^{\prime }}<t_{V^{\prime }}<t_{V}<t_{S}<1$
be associated to the infinite walks
![]() $S^{\prime },V^{\prime },V,S$
of Figure 9. Then,
$S^{\prime },V^{\prime },V,S$
of Figure 9. Then,
![]() $C([t_{S^{\prime }},t_{V^{\prime }}]\cup [t_{V},t_{S}])$
is the boundary of an interior component of the tile
$C([t_{S^{\prime }},t_{V^{\prime }}]\cup [t_{V},t_{S}])$
is the boundary of an interior component of the tile
![]() ${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
defined by (6.1). The closure of this component is homeomorphic to a closed disk.
${\mathcal{T}}={\mathcal{T}}(A,{\mathcal{D}})$
defined by (6.1). The closure of this component is homeomorphic to a closed disk.
Proof. We apply Theorem 3. We just need to prove that
![]() $(S^{\prime },S)$
and
$(S^{\prime },S)$
and
![]() $(V^{\prime },V)$
are outer identifications. This is done by checking that
$(V^{\prime },V)$
are outer identifications. This is done by checking that
The computations follow the algorithm of Theorem 2. For the identification
![]() $(S^{\prime },S)$
, we illustrate them in Figures 12–16. By Proposition 4.5, we can choose rather arbitrarily the reference points on the boundary in order to compute the winding numbers. Let us choose vertices of the hexagon
$(S^{\prime },S)$
, we illustrate them in Figures 12–16. By Proposition 4.5, we can choose rather arbitrarily the reference points on the boundary in order to compute the winding numbers. Let us choose vertices of the hexagon
![]() $Q$
as follows:
$Q$
as follows:
-
∙
 $t:=t_{C_{2}}$
(
$t:=t_{C_{2}}$
(
 $C_{2}=(0,1/3)$
) to compute
$C_{2}=(0,1/3)$
) to compute
 $w_{t_{S^{\prime }},t_{S}}=W(C(t),C([t_{S^{\prime }},t_{S}]))$
;
$w_{t_{S^{\prime }},t_{S}}=W(C(t),C([t_{S^{\prime }},t_{S}]))$
; -
∙
 $t^{\prime }:=t_{C_{5}}$
(
$t^{\prime }:=t_{C_{5}}$
(
 $C_{5}=(0,-1/3)$
) to compute
$C_{5}=(0,-1/3)$
) to compute
 $w_{t_{S^{\prime }},t_{S}}^{\prime }=W(C(t^{\prime }),C([0,t_{S^{\prime }}]\cup [t_{S},1]))$
.
$w_{t_{S^{\prime }},t_{S}}^{\prime }=W(C(t^{\prime }),C([0,t_{S^{\prime }}]\cup [t_{S},1]))$
.
Figures 12 and 13 show the curves
![]() $C_{n}(a_{n},b_{n})$
and
$C_{n}(a_{n},b_{n})$
and
![]() $D_{n}(a_{n},b_{n})$
that are used to compute these winding numbers. To determine which minimal value of
$D_{n}(a_{n},b_{n})$
that are used to compute these winding numbers. To determine which minimal value of
![]() $n$
gives us the right winding numbers, we apply the encircling method as described in the proof of Theorem 2. Here, if
$n$
gives us the right winding numbers, we apply the encircling method as described in the proof of Theorem 2. Here, if
![]() $||\cdot ||$
denotes the Euclidean norm, we have
$||\cdot ||$
denotes the Euclidean norm, we have
hence,
![]() $k=2$
and
$k=2$
and
![]() $\unicode[STIX]{x1D706}=2/3$
are suitable. We refer to the proof of Theorem 1 for the definition of these quantities. This allows us to determine a value of
$\unicode[STIX]{x1D706}=2/3$
are suitable. We refer to the proof of Theorem 1 for the definition of these quantities. This allows us to determine a value of
![]() $r$
for which
$r$
for which
![]() ${\mathcal{T}}\subset \mathbb{D}(0;r)$
. Indeed, again with the notations of the proof of Theorem 1,
${\mathcal{T}}\subset \mathbb{D}(0;r)$
. Indeed, again with the notations of the proof of Theorem 1,
![]() $A^{\prime }=A^{2},{\mathcal{D}}^{\prime }=A{\mathcal{D}}+{\mathcal{D}}$
, and a point in
$A^{\prime }=A^{2},{\mathcal{D}}^{\prime }=A{\mathcal{D}}+{\mathcal{D}}$
, and a point in
![]() ${\mathcal{T}}$
has the norm
${\mathcal{T}}$
has the norm
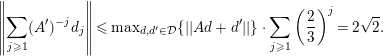 $$\begin{eqnarray}\left\Vert \mathop{\sum }_{j\geqslant 1}(A^{\prime })^{-j}d_{j}\right\Vert \leqslant \text{max}_{d,d^{\prime }\in {\mathcal{D}}}\{||Ad+d^{\prime }||\}\cdot \mathop{\sum }_{j\geqslant 1}\left(\frac{2}{3}\right)^{j}=2\sqrt{2}.\end{eqnarray}$$
$$\begin{eqnarray}\left\Vert \mathop{\sum }_{j\geqslant 1}(A^{\prime })^{-j}d_{j}\right\Vert \leqslant \text{max}_{d,d^{\prime }\in {\mathcal{D}}}\{||Ad+d^{\prime }||\}\cdot \mathop{\sum }_{j\geqslant 1}\left(\frac{2}{3}\right)^{j}=2\sqrt{2}.\end{eqnarray}$$
Performing the encircling method, we see that for
![]() $n=7$
the reference points lie outside of the covering by the disks (Figures 15 and 16). Computing the winding numbers of the reference points with respect to the approximations
$n=7$
the reference points lie outside of the covering by the disks (Figures 15 and 16). Computing the winding numbers of the reference points with respect to the approximations
![]() $C_{7}(a_{7},a_{7})$
and
$C_{7}(a_{7},a_{7})$
and
![]() $D_{7}(a_{7},b_{7})$
, we obtain the value
$D_{7}(a_{7},b_{7})$
, we obtain the value
![]() $1$
in both cases. Therefore,
$1$
in both cases. Therefore,
![]() $(S,S^{\prime })$
is an outer identification.
$(S,S^{\prime })$
is an outer identification.
Similar computations lead to
![]() $w_{t_{V^{\prime }},t_{V}}=w_{t_{V^{\prime }},t_{V}}^{\prime }=1$
; that is,
$w_{t_{V^{\prime }},t_{V}}=w_{t_{V^{\prime }},t_{V}}^{\prime }=1$
; that is,
![]() $(V^{\prime },V)$
is also an outer identification and Theorem 3 applies.◻
$(V^{\prime },V)$
is also an outer identification and Theorem 3 applies.◻
Remark 6.6. In fact, each simple closed curve of Theorem 6 is the boundary of an inner component. In other words, the tile
![]() ${\mathcal{T}}(A,{\mathcal{D}})$
is a countable union of topological closed disks, together with two points, and each disk intersects exactly two other disks, each at one point. Proving that all of the nontrivial identifications are outer makes use of the self-similarity of
${\mathcal{T}}(A,{\mathcal{D}})$
is a countable union of topological closed disks, together with two points, and each disk intersects exactly two other disks, each at one point. Proving that all of the nontrivial identifications are outer makes use of the self-similarity of
![]() ${\mathcal{T}}$
and involves further computations on the parametrization. Therefore, we postpone the proof to a forthcoming paper.
${\mathcal{T}}$
and involves further computations on the parametrization. Therefore, we postpone the proof to a forthcoming paper.
Remark 6.7. Theorems 5–7 obtained by our general method can be compared with the work of Ngai and Nguyen [Reference Ngai and NguyenNN03], where the cut points of the Heighway dragon are computed and its interior components are shown to be disklike. To obtain this topological information, Ngai and Nguyen analyze precisely the behavior of
![]() $n$
-fold iterations
$n$
-fold iterations
![]() ${\mathcal{P}}_{n}$
of the vertical unit segment
${\mathcal{P}}_{n}$
of the vertical unit segment
![]() ${\mathcal{P}}_{0}$
, whose limit in Hausdorff distance results in the Heighway dragon, and they describe the largest interior component of the Heighway dragon as the attractor of a GIFS. Our method also applies to this example (see Section 7.2), but we rather extract all the information directly from boundary approximations of the Heighway dragon, using our parametrization.
${\mathcal{P}}_{0}$
, whose limit in Hausdorff distance results in the Heighway dragon, and they describe the largest interior component of the Heighway dragon as the attractor of a GIFS. Our method also applies to this example (see Section 7.2), but we rather extract all the information directly from boundary approximations of the Heighway dragon, using our parametrization.
7 Further work
We give in this section several comments on the paper and present some ideas that will be worked out in forthcoming papers.
7.1 Description of interior components
We aim at developing methods in order to get very precise information on the wild topology of self-affine tiles, like the description of the boundary of interior components in terms of GIFSs (see [Reference Mauldin and WilliamsMW88]). Descriptions of this kind were obtained for the single examples of Figure 18 in [Reference Loridant and ThuswaldnerLT08, Reference Bernat, Loridant and ThuswaldnerBLT10] (canonical number system tile of
![]() $-2+i$
) or in [Reference Ngai and NguyenNN03] (Heighway dragon). We rather use our general boundary parametrization tool.
$-2+i$
) or in [Reference Ngai and NguyenNN03] (Heighway dragon). We rather use our general boundary parametrization tool.
7.2 Dealing with nontrivial identifications
In this paper, we restrict to the case where no pairs of identifications are crossing. This first step in the study of non-disklike tiles enables us to describe tiles with a reasonable topological complexity. Similar examples are the crystallographic replication tiles (see [Reference GelbrichGel94]) depicted in Figure 17. On the left is the Heighway dragon and on the right is a tile found in [Reference Loridant and LuoLL09, Figure 14]. They tile the plane with respect to the crystallographic groups
![]() $p4$
and
$p4$
and
![]() $p2$
, respectively. A boundary approximation of the Heighway dragon obtained via the parametrization method can also be found in this figure.
$p2$
, respectively. A boundary approximation of the Heighway dragon obtained via the parametrization method can also be found in this figure.

Figure 17. Tiles with no crossing pairs of identifications.

Figure 18. Tiles with crossing pairs of identifications.
However, we find in the literature examples where pairs of identifications are crossing. In Figure 18, we depict two such tiles with a wilder topology. The tile at the top is a canonical number system tile, associated with the basis
![]() $-2+i$
(see [Reference GilbertGil81]). The intersection of the central tile with some of its neighbors is a Cantor set (see [Reference Duan, Liu and TangDLT09]). It has a large set of nontrivial identifications.
$-2+i$
(see [Reference GilbertGil81]). The intersection of the central tile with some of its neighbors is a Cantor set (see [Reference Duan, Liu and TangDLT09]). It has a large set of nontrivial identifications.
At the bottom, we represent an example with an intermediate topological complexity. This self-similar tile Limhex was originally given as a triomino (a polygon composed of regular triangles) tiling generated by a pseudo substitution by Socolar (see [Reference SocolarSoc]). The substitution rule is depicted in the middle of Figure 18. The substitution is not edge to edge, like the substitution rule of Penrose tiling. Taking the
![]() $n\text{th}$
iterate and shrinking by the ratio
$n\text{th}$
iterate and shrinking by the ratio
![]() $1/2^{n}$
to renormalize, we obtain as a Hausdorff limit a fractal tile Limhex, whose IFS is given by
$1/2^{n}$
to renormalize, we obtain as a Hausdorff limit a fractal tile Limhex, whose IFS is given by
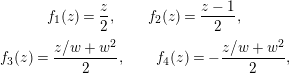 $$\begin{eqnarray}\displaystyle & \displaystyle f_{1}(z)=\frac{z}{2},\qquad f_{2}(z)=\frac{z-1}{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{3}(z)=\frac{z/w+w^{2}}{2},\qquad f_{4}(z)=-\frac{z/w+w^{2}}{2}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{1}(z)=\frac{z}{2},\qquad f_{2}(z)=\frac{z-1}{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{3}(z)=\frac{z/w+w^{2}}{2},\qquad f_{4}(z)=-\frac{z/w+w^{2}}{2}, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $w=e^{i\unicode[STIX]{x1D70B}/3}$
. In Figure 18, we can see the attractor Limhex of this IFS (up to some translation) together with its neighbors in the aperiodic tiling it generates. Here, the intersection of the central tile with a neighbor is either a simple arc or a single point.
$w=e^{i\unicode[STIX]{x1D70B}/3}$
. In Figure 18, we can see the attractor Limhex of this IFS (up to some translation) together with its neighbors in the aperiodic tiling it generates. Here, the intersection of the central tile with a neighbor is either a simple arc or a single point.
The coming step in our study will be to appropriately extend the definition of outer identification to such cases. Note that some identifications on the boundary of the tiles in Figure 18 do not contribute to a new interior component, but rather lead to a hole. We may call them inner identifications, but, for now, we are looking for typical examples in order to axiomatize and propose the next tractable class of such identifications.