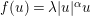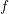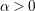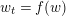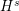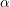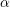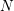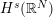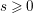1 Introduction
This paper is concerned with regularity of solutions of two well known and well studied semilinear evolution equations, the semilinear heat equation,
and the semilinear Schrödinger equation,
in
![]() $\mathbb{R}^{N}$
, where
$\mathbb{R}^{N}$
, where
![]() $\unicode[STIX]{x1D6FC}>0$
and
$\unicode[STIX]{x1D6FC}>0$
and
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}$
,
$\unicode[STIX]{x1D706}\in \mathbb{C}$
,
![]() $\unicode[STIX]{x1D706}\not =0$
. More precisely, we allow the initial value
$\unicode[STIX]{x1D706}\not =0$
. More precisely, we allow the initial value
![]() $u_{0}$
to be infinitely smooth, and we study the loss of regularity due to the nonlinear term. Therefore, we are particularly interested in small values of
$u_{0}$
to be infinitely smooth, and we study the loss of regularity due to the nonlinear term. Therefore, we are particularly interested in small values of
![]() $\unicode[STIX]{x1D6FC}>0$
. Let
$\unicode[STIX]{x1D6FC}>0$
. Let
![]() $f(u)=|u|^{\unicode[STIX]{x1D6FC}}u$
, with
$f(u)=|u|^{\unicode[STIX]{x1D6FC}}u$
, with
![]() $0<\unicode[STIX]{x1D6FC}<1$
. As a point function
$0<\unicode[STIX]{x1D6FC}<1$
. As a point function
![]() $f$
is
$f$
is
![]() $C^{1}$
but not
$C^{1}$
but not
![]() $C^{2}$
. Formally, this might be considered to be an obstacle to the regularity of solutions of (1.1) and (1.2). Indeed, in order to prove the regularity of the solutions of (1.1) and (1.2) (for instance, by a fixed-point argument), one uses the regularity of the nonlinear term. However, the relationship between the regularity of
$C^{2}$
. Formally, this might be considered to be an obstacle to the regularity of solutions of (1.1) and (1.2). Indeed, in order to prove the regularity of the solutions of (1.1) and (1.2) (for instance, by a fixed-point argument), one uses the regularity of the nonlinear term. However, the relationship between the regularity of
![]() $f$
and the regularity of the solution is not a simple one. To see this, suppose that
$f$
and the regularity of the solution is not a simple one. To see this, suppose that
![]() $u$
is
$u$
is
![]() $C^{2}(\mathbb{R}^{N},\mathbb{C})$
,
$C^{2}(\mathbb{R}^{N},\mathbb{C})$
,
![]() $u(x_{0})=0$
and
$u(x_{0})=0$
and
![]() $\unicode[STIX]{x1D6FB}u(x_{0})\not =0$
for some
$\unicode[STIX]{x1D6FB}u(x_{0})\not =0$
for some
![]() $x_{0}\in \mathbb{R}^{N}$
, then
$x_{0}\in \mathbb{R}^{N}$
, then
![]() $f(u)\not \in C^{2}(\mathbb{R}^{N},\mathbb{C})$
. In particular, if
$f(u)\not \in C^{2}(\mathbb{R}^{N},\mathbb{C})$
. In particular, if
![]() $u$
is a solution of, for example, (1.1), then also
$u$
is a solution of, for example, (1.1), then also
![]() $u_{t}-\unicode[STIX]{x1D6E5}u\not \in C^{2}(\mathbb{R}^{N},\mathbb{C})$
. On the other hand, for any reasonable initial value, for example in
$u_{t}-\unicode[STIX]{x1D6E5}u\not \in C^{2}(\mathbb{R}^{N},\mathbb{C})$
. On the other hand, for any reasonable initial value, for example in
![]() $C_{0}(\mathbb{R}^{N})$
, the corresponding solution of (1.1) will, in fact, be
$C_{0}(\mathbb{R}^{N})$
, the corresponding solution of (1.1) will, in fact, be
![]() $C^{2}$
in space for
$C^{2}$
in space for
![]() $t>0$
by standard parabolic regularity. Thus, the non-regularity of
$t>0$
by standard parabolic regularity. Thus, the non-regularity of
![]() $f(u)$
does not immediately imply the non-regularity of
$f(u)$
does not immediately imply the non-regularity of
![]() $u$
.
$u$
.
The question of regularity is strongly related to the question of well-posedness. Recall that an evolution equation, such as (1.1) or (1.2), is locally well-posed in a Banach space
![]() $X$
if for every
$X$
if for every
![]() $u_{0}\in X$
there exist
$u_{0}\in X$
there exist
![]() $T>0$
and a solution
$T>0$
and a solution
![]() $u\in C([0,T],X)$
such that
$u\in C([0,T],X)$
such that
![]() $u(0)=0$
. In addition, the solution is required to be unique in some sense, not always in
$u(0)=0$
. In addition, the solution is required to be unique in some sense, not always in
![]() $C([0,T],X)$
, and is also required to depend continuously, again in some appropriate sense, on the initial value
$C([0,T],X)$
, and is also required to depend continuously, again in some appropriate sense, on the initial value
![]() $u_{0}$
. The key point for our purposes is that if
$u_{0}$
. The key point for our purposes is that if
![]() $X$
is a positive-order Sobolev space, whose elements have a certain degree of regularity, the resulting solution maintains this regularity.
$X$
is a positive-order Sobolev space, whose elements have a certain degree of regularity, the resulting solution maintains this regularity.
Specifically, if we wish to use a standard perturbation argument to prove that the Cauchy problem for either equation (1.1) or (1.2) is locally well-posed in
![]() $H^{s}(\mathbb{R}^{N})$
for some given
$H^{s}(\mathbb{R}^{N})$
for some given
![]() $s>0$
, we are confronted with two different requirements on
$s>0$
, we are confronted with two different requirements on
![]() $\unicode[STIX]{x1D6FC}$
. On the one hand, we need that the nonlinear term be controlled by the linear flow. This translates (formally) as the condition
$\unicode[STIX]{x1D6FC}$
. On the one hand, we need that the nonlinear term be controlled by the linear flow. This translates (formally) as the condition
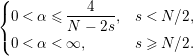 $$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle 0<\unicode[STIX]{x1D6FC}\leqslant \frac{4}{N-2s},\quad & s<N/2,\\ 0<\unicode[STIX]{x1D6FC}<\infty ,\quad & s\geqslant N/2.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}ll@{}}\displaystyle 0<\unicode[STIX]{x1D6FC}\leqslant \frac{4}{N-2s},\quad & s<N/2,\\ 0<\unicode[STIX]{x1D6FC}<\infty ,\quad & s\geqslant N/2.\end{array}\right. & & \displaystyle\end{eqnarray}$$
On the other hand, in order to carry out the perturbation argument in
![]() $H^{s}$
, the nonlinear term must be sufficiently smooth. When
$H^{s}$
, the nonlinear term must be sufficiently smooth. When
![]() $\unicode[STIX]{x1D6FC}$
is not an even integer, then
$\unicode[STIX]{x1D6FC}$
is not an even integer, then
![]() $\unicode[STIX]{x1D6FC}$
must be large enough so that
$\unicode[STIX]{x1D6FC}$
must be large enough so that
![]() $f(u)=|u|^{\unicode[STIX]{x1D6FC}}u$
is sufficiently regular. In the case of the simplest perturbation argument requiring an estimate of
$f(u)=|u|^{\unicode[STIX]{x1D6FC}}u$
is sufficiently regular. In the case of the simplest perturbation argument requiring an estimate of
![]() $|u|^{\unicode[STIX]{x1D6FC}}u$
in
$|u|^{\unicode[STIX]{x1D6FC}}u$
in
![]() $H^{s}(\mathbb{R}^{N})$
, this leads to the condition
$H^{s}(\mathbb{R}^{N})$
, this leads to the condition
(See, e.g., [Reference Ribaud20, Reference Molinet, Ribaud and Youssfi16] for the heat equation and [Reference Kato12, Reference Kato13, Reference Cazenave and Weissler8, Reference Ginibre, Ozawa and Velo11, Reference Kato14, Reference Nakamura and Ozawa17, Reference Pecher19, Reference Uchizono and Wada22, Reference Fang and Han10] for the Schrödinger equation.)
Since the first condition (1.3) is related to scaling properties of the equation (see [Reference Tao21, Section 3.1], and in particular the discussion on p. 118), it can be considered as natural. In fact, in some cases it is known that if this condition is not satisfied, then the problem is not well-posed in
![]() $H^{s}(\mathbb{R}^{N})$
(see, e.g., [Reference Molinet, Ribaud and Youssfi16, Reference Christ, Colliander and Tao9, Reference Burq, Gérard and Tzvetkov5, Reference Carles6, Reference Alazard and Carles2]). On the other hand, (1.4) might appear as a purely technical condition which one should be able to remove by a more appropriate argument. Indeed, one can sometimes improve condition (1.4) by using the fact that one time derivative is like two space derivatives, but we are still left with the condition
$H^{s}(\mathbb{R}^{N})$
(see, e.g., [Reference Molinet, Ribaud and Youssfi16, Reference Christ, Colliander and Tao9, Reference Burq, Gérard and Tzvetkov5, Reference Carles6, Reference Alazard and Carles2]). On the other hand, (1.4) might appear as a purely technical condition which one should be able to remove by a more appropriate argument. Indeed, one can sometimes improve condition (1.4) by using the fact that one time derivative is like two space derivatives, but we are still left with the condition
(See [Reference Kato13, Reference Pecher19, Reference Uchizono and Wada22, Reference Fang and Han10].)
The purpose of this paper, as opposed to the above cited papers, is to show that in certain cases “technical” restrictions such as (1.4) and (1.5) are not purely technical, but impose genuine limitations on the regularity of the solution. More precisely, we show that condition (1.3) is not always sufficient to imply local well-posedness of (1.1) and (1.2) in
![]() $H^{s}$
. (See Remarks 1.3 and 1.6, and Theorem 1.10.) In fact, we prove under various circumstances that there exist initial values
$H^{s}$
. (See Remarks 1.3 and 1.6, and Theorem 1.10.) In fact, we prove under various circumstances that there exist initial values
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
for which (1.1) or (1.2) cannot have a local solution with a certain degree of regularity. To the best of our knowledge, there are no previous results of this type.
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
for which (1.1) or (1.2) cannot have a local solution with a certain degree of regularity. To the best of our knowledge, there are no previous results of this type.
Our first result concerns the nonlinear heat equation (1.1), and is, in fact, optimal. We recall that the Cauchy problem (1.1) is locally well-posed in
![]() $C_{0}(\mathbb{R}^{N})$
; that is, for any
$C_{0}(\mathbb{R}^{N})$
; that is, for any
![]() $u_{0}\in C_{0}(\mathbb{R}^{N})$
, there exist a maximal existence time
$u_{0}\in C_{0}(\mathbb{R}^{N})$
, there exist a maximal existence time
![]() $T_{\max }>0$
and a unique solution
$T_{\max }>0$
and a unique solution
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1). Let
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1). Let
![]() $0<\unicode[STIX]{x1D6FC}<1$
, let
$0<\unicode[STIX]{x1D6FC}<1$
, let
![]() $u_{0}$
be smooth, and let
$u_{0}$
be smooth, and let
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
be the resulting maximal solution of (1.1). It is known that, given any
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
be the resulting maximal solution of (1.1). It is known that, given any
![]() $0<T<T_{\max }$
,
$0<T<T_{\max }$
,
![]() $\unicode[STIX]{x2202}_{t}u$
,
$\unicode[STIX]{x2202}_{t}u$
,
![]() $\unicode[STIX]{x1D6FB}\unicode[STIX]{x2202}_{t}u$
, and all space derivatives of
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x2202}_{t}u$
, and all space derivatives of
![]() $u$
of order up to
$u$
of order up to
![]() $3$
belong to
$3$
belong to
![]() $C([0,T]\times \mathbb{R}^{N})$
. Furthermore, the spatial derivatives of order
$C([0,T]\times \mathbb{R}^{N})$
. Furthermore, the spatial derivatives of order
![]() $3$
are
$3$
are
![]() $\unicode[STIX]{x1D6FC}$
-Hölder continuous; that is,
$\unicode[STIX]{x1D6FC}$
-Hölder continuous; that is,
where
![]() $|w|_{\ell }$
is defined by
$|w|_{\ell }$
is defined by
for
![]() $\ell >0$
and
$\ell >0$
and
![]() $w\in C(\mathbb{R}^{N})$
(see Theorem A.1 in the Appendix for a precise statement). The theorem below shows that the
$w\in C(\mathbb{R}^{N})$
(see Theorem A.1 in the Appendix for a precise statement). The theorem below shows that the
![]() $\unicode[STIX]{x1D6FC}$
-Hölder continuity cannot, in general, be improved, in the sense that one cannot replace
$\unicode[STIX]{x1D6FC}$
-Hölder continuity cannot, in general, be improved, in the sense that one cannot replace
![]() $\unicode[STIX]{x1D6FC}$
by
$\unicode[STIX]{x1D6FC}$
by
![]() $\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6FC}$
.
Theorem 1.1. Let
![]() $0<\unicode[STIX]{x1D6FC}<1$
, and let
$0<\unicode[STIX]{x1D6FC}<1$
, and let
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
. There exists an initial value
$\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
. There exists an initial value
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that the corresponding maximal solution
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that the corresponding maximal solution
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) is three times continuously differentiable with respect to the space variable and
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) is three times continuously differentiable with respect to the space variable and
for all
![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}\leqslant 1$
and all
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}\leqslant 1$
and all
![]() $0\leqslant s<t<T_{\max }$
with
$0\leqslant s<t<T_{\max }$
with
![]() $t$
sufficiently small.
$t$
sufficiently small.
Theorem 1.1 has the immediate following corollary, by using Sobolev’s embedding theorem (see (1.15)).
Corollary 1.2. Let
![]() $0<\unicode[STIX]{x1D6FC}<1$
. There exists an initial value
$0<\unicode[STIX]{x1D6FC}<1$
. There exists an initial value
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that the corresponding maximal solution
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that the corresponding maximal solution
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) does not belong to
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) does not belong to
![]() $L^{1}((0,T),H^{s,p}(\mathbb{R}^{N}))$
if
$L^{1}((0,T),H^{s,p}(\mathbb{R}^{N}))$
if
![]() $s>3+\frac{N}{p}+\unicode[STIX]{x1D6FC}$
,
$s>3+\frac{N}{p}+\unicode[STIX]{x1D6FC}$
,
![]() $1<p<\infty$
, and
$1<p<\infty$
, and
![]() $0<T<T_{\max }$
.
$0<T<T_{\max }$
.
Remark 1.3. The initial value
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
can be chosen arbitrarily small (in any space). See Remark 3.4. Corollary 1.2 therefore implies that
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
can be chosen arbitrarily small (in any space). See Remark 3.4. Corollary 1.2 therefore implies that
![]() $s\leqslant 3+\frac{N}{p}+\unicode[STIX]{x1D6FC}$
,
$s\leqslant 3+\frac{N}{p}+\unicode[STIX]{x1D6FC}$
,
![]() $1<p<\infty$
is a necessary condition for (1.1) to be locally well-posed in
$1<p<\infty$
is a necessary condition for (1.1) to be locally well-posed in
![]() $H^{s,p}(\mathbb{R}^{N})$
, even in an arbitrarily small ball.
$H^{s,p}(\mathbb{R}^{N})$
, even in an arbitrarily small ball.
Remark 1.4. We should observe that formula (1.8) does not imply that
![]() $|\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D6E5}u(t)|_{\unicode[STIX]{x1D6FD}}$
is infinite for any given value of
$|\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D6E5}u(t)|_{\unicode[STIX]{x1D6FD}}$
is infinite for any given value of
![]() $0<t<T_{\max }$
. On the other hand, it is stronger than saying that
$0<t<T_{\max }$
. On the other hand, it is stronger than saying that
![]() $\sup _{0\leqslant t\leqslant T}|\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D6E5}u(t)|_{\unicode[STIX]{x1D6FD}}=\infty$
. Similarly, Corollary 1.2 does not guarantee that
$\sup _{0\leqslant t\leqslant T}|\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D6E5}u(t)|_{\unicode[STIX]{x1D6FD}}=\infty$
. Similarly, Corollary 1.2 does not guarantee that
![]() $u(t)\not \in H^{s}(\mathbb{R}^{N})$
for any given value of
$u(t)\not \in H^{s}(\mathbb{R}^{N})$
for any given value of
![]() $0<t<T_{\max }$
.
$0<t<T_{\max }$
.
Before stating our next result, we make some comments on the proof of Theorem 1.1. The key idea is to consider equation (1.1) as a perturbation of the ordinary differential equation
with the same initial condition
![]() $w(0,\cdot )=u_{0}(\cdot )$
. As we shall see by a straightforward calculation (see Section 2), (1.9) produces a loss of spatial regularity. For example, in dimension
$w(0,\cdot )=u_{0}(\cdot )$
. As we shall see by a straightforward calculation (see Section 2), (1.9) produces a loss of spatial regularity. For example, in dimension
![]() $N=1$
, if
$N=1$
, if
![]() $u_{0}(x)=x$
in a neighborhood of
$u_{0}(x)=x$
in a neighborhood of
![]() $0$
, then the resulting solution
$0$
, then the resulting solution
![]() $w(t,x)$
of (1.9) will not be twice differentiable at
$w(t,x)$
of (1.9) will not be twice differentiable at
![]() $x=0$
for
$x=0$
for
![]() $t>0$
. Moreover, for the perturbed equation
$t>0$
. Moreover, for the perturbed equation
where
![]() $h$
is sufficiently smooth, the same loss of regularity occurs (see Theorem 2.1). Let now
$h$
is sufficiently smooth, the same loss of regularity occurs (see Theorem 2.1). Let now
![]() $u$
be a solution of the nonlinear heat equation (1.1), and set
$u$
be a solution of the nonlinear heat equation (1.1), and set
![]() $h=\unicode[STIX]{x1D6E5}u$
. It follows that
$h=\unicode[STIX]{x1D6E5}u$
. It follows that
![]() $u_{t}=\unicode[STIX]{x1D706}|u|^{\unicode[STIX]{x1D6FC}}u+h$
. Thus, we see that for appropriate
$u_{t}=\unicode[STIX]{x1D706}|u|^{\unicode[STIX]{x1D6FC}}u+h$
. Thus, we see that for appropriate
![]() $u_{0}$
, if
$u_{0}$
, if
![]() $h$
is sufficiently smooth, then
$h$
is sufficiently smooth, then
![]() $u(t)$
is not
$u(t)$
is not
![]() $C^{2}$
in space for small
$C^{2}$
in space for small
![]() $t>0$
. Since we know that
$t>0$
. Since we know that
![]() $u(t)$
is
$u(t)$
is
![]() $C^{2}$
for
$C^{2}$
for
![]() $t>0$
, this implies that
$t>0$
, this implies that
![]() $h=\unicode[STIX]{x1D6E5}u$
is not too regular. Applying the precise regularity statement of Theorem 2.1 gives the conclusion of Theorem 1.1.
$h=\unicode[STIX]{x1D6E5}u$
is not too regular. Applying the precise regularity statement of Theorem 2.1 gives the conclusion of Theorem 1.1.
It turns out that the same arguments can be used to prove ill-posedness for the nonlinear Schrödinger equation (1.2). This yields the following analogue of Corollary 1.2.
Theorem 1.5. Let
![]() $0<\unicode[STIX]{x1D6FC}<1$
, let
$0<\unicode[STIX]{x1D6FC}<1$
, let
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
, and suppose that
$\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
, and suppose that
![]() $s>3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
. There exists
$s>3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
. There exists
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that there is no
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that there is no
![]() $T>0$
for which there exists a solution
$T>0$
for which there exists a solution
![]() $u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (1.2).
$u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (1.2).
Remark 1.6. Theorem 1.5 implies that
![]() $s\leqslant 3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
is a necessary condition for (1.2) to be locally well-posed in
$s\leqslant 3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
is a necessary condition for (1.2) to be locally well-posed in
![]() $H^{s}(\mathbb{R}^{N})$
, even in an arbitrarily small ball (see Remark 3.4).
$H^{s}(\mathbb{R}^{N})$
, even in an arbitrarily small ball (see Remark 3.4).
Theorem 1.5 turns out to be a specific case of an analogous result for the complex Ginzburg–Landau equation (see Theorem 3.2 below).
As pointed out in Remark 1.4, Theorem 1.1 and Corollary 1.2 do not guarantee the lack of spatial regularity of the solution
![]() $u$
of (1.1) at any fixed
$u$
of (1.1) at any fixed
![]() $t>0$
. The following theorem gives an example of loss of spatial regularity for every
$t>0$
. The following theorem gives an example of loss of spatial regularity for every
![]() $t>0$
.
$t>0$
.
Theorem 1.7. Let
![]() $0<\unicode[STIX]{x1D6FC}<2$
, and let
$0<\unicode[STIX]{x1D6FC}<2$
, and let
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
. There exists an initial value
$\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
. There exists an initial value
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that the corresponding maximal solution
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that the corresponding maximal solution
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) satisfies
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) satisfies
![]() $u(t)\not \in H^{s,p}(\mathbb{R}^{N})$
for all sufficiently small
$u(t)\not \in H^{s,p}(\mathbb{R}^{N})$
for all sufficiently small
![]() $0<t<T_{\max }$
if
$0<t<T_{\max }$
if
![]() $1<p<\infty$
and
$1<p<\infty$
and
![]() $s>5+\frac{1}{p}$
.
$s>5+\frac{1}{p}$
.
Remark 1.8. As observed for previous results, the initial value
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
in Theorem 1.7 can be chosen arbitrarily small (in any space). See Remark 4.3.
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
in Theorem 1.7 can be chosen arbitrarily small (in any space). See Remark 4.3.
Unlike the proof of Theorem 1.1, the proof of Theorem 1.7 treats the nonlinear term
![]() $|u|^{\unicode[STIX]{x1D6FC}}u$
as a perturbation of the linear heat equation, via the standard Duhamel formula. More precisely, for appropriate initial values we show that the integral term
$|u|^{\unicode[STIX]{x1D6FC}}u$
as a perturbation of the linear heat equation, via the standard Duhamel formula. More precisely, for appropriate initial values we show that the integral term
can never be in
![]() $H^{s,p}(\mathbb{R}^{N})$
if
$H^{s,p}(\mathbb{R}^{N})$
if
![]() $s>5+\frac{1}{p}$
. One key idea in the proof is to express
$s>5+\frac{1}{p}$
. One key idea in the proof is to express
![]() $|u(t,x^{\prime },y)|^{\unicode[STIX]{x1D6FC}}u(t,x^{\prime },y)=C(x^{\prime })\unicode[STIX]{x1D6FE}(t)|y|^{\unicode[STIX]{x1D6FC}}y+\widetilde{w}(t,x^{\prime },y)$
, where
$|u(t,x^{\prime },y)|^{\unicode[STIX]{x1D6FC}}u(t,x^{\prime },y)=C(x^{\prime })\unicode[STIX]{x1D6FE}(t)|y|^{\unicode[STIX]{x1D6FC}}y+\widetilde{w}(t,x^{\prime },y)$
, where
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
and
$x^{\prime }\in \mathbb{R}^{N-1}$
and
![]() $y\in \mathbb{R}$
, with
$y\in \mathbb{R}$
, with
![]() $|\widetilde{w}(t,x^{\prime },y)|\leqslant C|y|^{\unicode[STIX]{x1D6FC}+2}$
. This decomposition enables us to explicitly compute
$|\widetilde{w}(t,x^{\prime },y)|\leqslant C|y|^{\unicode[STIX]{x1D6FC}+2}$
. This decomposition enables us to explicitly compute
![]() $\unicode[STIX]{x2202}_{y}^{5}e^{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}}{\mathcal{I}}$
at
$\unicode[STIX]{x2202}_{y}^{5}e^{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}}{\mathcal{I}}$
at
![]() $y=0$
, which (if
$y=0$
, which (if
![]() $\unicode[STIX]{x1D6FC}<2$
) goes to
$\unicode[STIX]{x1D6FC}<2$
) goes to
![]() $\infty$
as
$\infty$
as
![]() $\unicode[STIX]{x1D700}\downarrow 0$
, uniformly for
$\unicode[STIX]{x1D700}\downarrow 0$
, uniformly for
![]() $x^{\prime }$
in a neighborhood of
$x^{\prime }$
in a neighborhood of
![]() $0$
. This shows that
$0$
. This shows that
![]() ${\mathcal{I}}$
cannot be
${\mathcal{I}}$
cannot be
![]() $C^{5}$
with respect to
$C^{5}$
with respect to
![]() $y$
, and the result then follows from the one-dimensional Sobolev embedding theorem. We insist on this last point; since the proof is based on a one-dimensional argument, the condition on
$y$
, and the result then follows from the one-dimensional Sobolev embedding theorem. We insist on this last point; since the proof is based on a one-dimensional argument, the condition on
![]() $s,p$
in the statement of Theorem 1.7 is independent of the space dimension
$s,p$
in the statement of Theorem 1.7 is independent of the space dimension
![]() $N$
.
$N$
.
On the other hand, in Corollary 1.2, the condition on
![]() $s,p$
does depend on the space dimension, since we deduce the result from Theorem 1.1 by the
$s,p$
does depend on the space dimension, since we deduce the result from Theorem 1.1 by the
![]() $N$
-dimensional Sobolev embedding theorem. This is perhaps only a technical problem. Indeed, the proof of Theorem 1.1 is also based on a one-dimensional argument. However, the structure of that proof, via an argument by contradiction, does not seem to allow the application of the one-dimensional Sobolev embedding theorem.
$N$
-dimensional Sobolev embedding theorem. This is perhaps only a technical problem. Indeed, the proof of Theorem 1.1 is also based on a one-dimensional argument. However, the structure of that proof, via an argument by contradiction, does not seem to allow the application of the one-dimensional Sobolev embedding theorem.
For our last result, we introduce a very weak notion of local well-posedness for small data, which is weaker than the general notion described earlier in the introduction. Recall that (1.1) is locally well-posed in
![]() $C_{0}(\mathbb{R}^{N})$
, and
$C_{0}(\mathbb{R}^{N})$
, and
![]() $T_{\max }(u_{0})$
is the maximal existence time of the solution corresponding to the initial value
$T_{\max }(u_{0})$
is the maximal existence time of the solution corresponding to the initial value
![]() $u_{0}$
.
$u_{0}$
.
Definition 1.9. Let
![]() $s\geqslant 0$
, let
$s\geqslant 0$
, let
![]() $\unicode[STIX]{x1D6FC}>0$
, and let
$\unicode[STIX]{x1D6FC}>0$
, and let
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}$
. We say that (1.1) is locally well-posed for small data in
$\unicode[STIX]{x1D706}\in \mathbb{C}$
. We say that (1.1) is locally well-posed for small data in
![]() $H^{s}(\mathbb{R}^{N})$
if there exist
$H^{s}(\mathbb{R}^{N})$
if there exist
![]() $\unicode[STIX]{x1D6FF},T>0$
such that if
$\unicode[STIX]{x1D6FF},T>0$
such that if
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
and
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
and
![]() $\Vert u_{0}\Vert _{H^{s}}\leqslant \unicode[STIX]{x1D6FF}$
, then the corresponding solution
$\Vert u_{0}\Vert _{H^{s}}\leqslant \unicode[STIX]{x1D6FF}$
, then the corresponding solution
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) satisfies
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
of (1.1) satisfies
![]() $T_{\max }(u_{0})\geqslant T$
and
$T_{\max }(u_{0})\geqslant T$
and
![]() $u(t)\in H^{s}(\mathbb{R}^{N})$
for all
$u(t)\in H^{s}(\mathbb{R}^{N})$
for all
![]() $0\leqslant t\leqslant T$
.
$0\leqslant t\leqslant T$
.
Theorem 1.10. Let
![]() $0<\unicode[STIX]{x1D6FC}<2$
, and let
$0<\unicode[STIX]{x1D6FC}<2$
, and let
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}$
with
$\unicode[STIX]{x1D706}\in \mathbb{R}$
with
![]() $\unicode[STIX]{x1D706}>0$
. If
$\unicode[STIX]{x1D706}>0$
. If
then for every
![]() $s\geqslant 0$
, the Cauchy problem (1.1) is not locally well-posed for small data in
$s\geqslant 0$
, the Cauchy problem (1.1) is not locally well-posed for small data in
![]() $H^{s}(\mathbb{R}^{N})$
.
$H^{s}(\mathbb{R}^{N})$
.
The rest of the paper is organized as follows. We recall below the definitions of the various function spaces we use, and certain of their properties. In Section 2, we study regularity of solutions to the ordinary differential equation (1.9), and to the perturbed equation (1.10). In particular, we show (Theorem 2.1) that if
![]() $h$
is sufficiently smooth, then (1.9) produces a singularity for a certain class of smooth data. In Section 3, we apply this result to prove Theorems 1.1 and 1.5, as well as a similar result for a complex Ginzburg–Landau equation (Theorem 3.2). In Section 4, we prove Theorems 1.7 and 1.10.
$h$
is sufficiently smooth, then (1.9) produces a singularity for a certain class of smooth data. In Section 3, we apply this result to prove Theorems 1.1 and 1.5, as well as a similar result for a complex Ginzburg–Landau equation (Theorem 3.2). In Section 4, we prove Theorems 1.7 and 1.10.
We make one final remark about our results. Throughout this paper, we consider small values of
![]() $\unicode[STIX]{x1D6FC}$
, either
$\unicode[STIX]{x1D6FC}$
, either
![]() $0<\unicode[STIX]{x1D6FC}<1$
or
$0<\unicode[STIX]{x1D6FC}<1$
or
![]() $0<\unicode[STIX]{x1D6FC}<2$
. It is likely that analogous results can be proved for larger values of
$0<\unicode[STIX]{x1D6FC}<2$
. It is likely that analogous results can be proved for larger values of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Notation and function spaces. Throughout this paper, we consider function spaces of complex-valued functions.
![]() $L^{p}(\mathbb{R}^{N})$
, for
$L^{p}(\mathbb{R}^{N})$
, for
![]() $1\leqslant p\leqslant \infty$
, is the usual Lebesgue space, with norm
$1\leqslant p\leqslant \infty$
, is the usual Lebesgue space, with norm
![]() $\Vert \cdot \Vert _{L^{p}}$
. We denote by
$\Vert \cdot \Vert _{L^{p}}$
. We denote by
![]() $C_{0}(\mathbb{R}^{N})$
the space of continuous functions on
$C_{0}(\mathbb{R}^{N})$
the space of continuous functions on
![]() $\mathbb{R}^{N}$
that vanish at infinity, equipped with the sup norm.
$\mathbb{R}^{N}$
that vanish at infinity, equipped with the sup norm.
![]() $H^{s,p}(\mathbb{R}^{N})$
and
$H^{s,p}(\mathbb{R}^{N})$
and
![]() $H^{s}(\mathbb{R}^{N})=H^{s,2}(\mathbb{R}^{N})$
, for
$H^{s}(\mathbb{R}^{N})=H^{s,2}(\mathbb{R}^{N})$
, for
![]() $s\geqslant 0$
and
$s\geqslant 0$
and
![]() $1<p<\infty$
, are the usual Sobolev spaces, and the corresponding norms are denoted by
$1<p<\infty$
, are the usual Sobolev spaces, and the corresponding norms are denoted by
![]() $\Vert \cdot \Vert _{H^{s}}$
and
$\Vert \cdot \Vert _{H^{s}}$
and
![]() $\Vert \cdot \Vert _{H^{s,p}}$
. In particular,
$\Vert \cdot \Vert _{H^{s,p}}$
. In particular,
and
![]() $\Vert u\Vert _{H^{s,p}}\approx \sum _{|\ell |\leqslant s}\Vert \unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}u\Vert _{L^{p}}$
if
$\Vert u\Vert _{H^{s,p}}\approx \sum _{|\ell |\leqslant s}\Vert \unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}u\Vert _{L^{p}}$
if
![]() $s$
is an integer (see, e.g., [Reference Bergh and Löfström4, Theorem 6.2.3]).
$s$
is an integer (see, e.g., [Reference Bergh and Löfström4, Theorem 6.2.3]).
In the proof of Theorem 1.7, we use the property that if
![]() $u=u(x_{1},x_{2})$
with
$u=u(x_{1},x_{2})$
with
![]() $x_{1}\in \mathbb{R}^{m}$
,
$x_{1}\in \mathbb{R}^{m}$
,
![]() $x_{2}\in \mathbb{R}^{n}$
, and if
$x_{2}\in \mathbb{R}^{n}$
, and if
![]() $1<p<\infty$
and
$1<p<\infty$
and
![]() $s\geqslant 0$
, then
$s\geqslant 0$
, then
Inequality (1.14) with
![]() $C=1$
is immediate when
$C=1$
is immediate when
![]() $s$
is an integer. (The left-hand side has fewer terms than the right-hand side.) The general case follows by complex interpolation. Indeed, suppose that
$s$
is an integer. (The left-hand side has fewer terms than the right-hand side.) The general case follows by complex interpolation. Indeed, suppose that
![]() $s$
is not an integer, fix two integers
$s$
is not an integer, fix two integers
![]() $0\leqslant s_{0}<s<s_{1}$
and let
$0\leqslant s_{0}<s<s_{1}$
and let
![]() $0<\unicode[STIX]{x1D703}<1$
be defined by
$0<\unicode[STIX]{x1D703}<1$
be defined by
![]() $s=(1-\unicode[STIX]{x1D703})s_{0}+\unicode[STIX]{x1D703}s_{1}$
. It follows that
$s=(1-\unicode[STIX]{x1D703})s_{0}+\unicode[STIX]{x1D703}s_{1}$
. It follows that
![]() $H^{s,p}(\mathbb{R}^{m+n})=(H^{s_{0},p}(\mathbb{R}^{m+n}),H^{s_{1},p}(\mathbb{R}^{m+n}))_{[\unicode[STIX]{x1D703}]}$
and
$H^{s,p}(\mathbb{R}^{m+n})=(H^{s_{0},p}(\mathbb{R}^{m+n}),H^{s_{1},p}(\mathbb{R}^{m+n}))_{[\unicode[STIX]{x1D703}]}$
and
![]() $H^{s,p}(\mathbb{R}^{n})=(H^{s_{0},p}(\mathbb{R}^{n}),H^{s_{1},p}(\mathbb{R}^{n}))_{[\unicode[STIX]{x1D703}]}$
(see [Reference Bergh and Löfström4, Theorem 6.4.5]). This last property implies that
$H^{s,p}(\mathbb{R}^{n})=(H^{s_{0},p}(\mathbb{R}^{n}),H^{s_{1},p}(\mathbb{R}^{n}))_{[\unicode[STIX]{x1D703}]}$
(see [Reference Bergh and Löfström4, Theorem 6.4.5]). This last property implies that
(see [Reference Bergh and Löfström4, Theorem 5.1.2]). Estimate (1.14) now follows by complex interpolation between the estimates for
![]() $s=s_{0}$
and
$s=s_{0}$
and
![]() $s=s_{1}$
.
$s=s_{1}$
.
We use Sobolev’s embedding into Hölder spaces. Recall definition (1.7). Given any
![]() $j\in \mathbb{N}$
and
$j\in \mathbb{N}$
and
![]() $0<\ell <1$
, the Hölder space
$0<\ell <1$
, the Hölder space
![]() $C^{j,\ell }(\overline{\mathbb{R}^{N}})$
is the space of functions
$C^{j,\ell }(\overline{\mathbb{R}^{N}})$
is the space of functions
![]() $u$
whose derivatives of order
$u$
whose derivatives of order
![]() ${\leqslant}j$
are all bounded and uniformly continuous, and such that
${\leqslant}j$
are all bounded and uniformly continuous, and such that
![]() $|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u|_{\ell }<\infty$
for all multi-indices
$|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u|_{\ell }<\infty$
for all multi-indices
![]() $\unicode[STIX]{x1D6FE}$
with
$\unicode[STIX]{x1D6FE}$
with
![]() $|\unicode[STIX]{x1D6FE}|=j$
.
$|\unicode[STIX]{x1D6FE}|=j$
.
![]() $C^{j,\ell }(\overline{\mathbb{R}^{N}})$
is a Banach space when equipped with the norm
$C^{j,\ell }(\overline{\mathbb{R}^{N}})$
is a Banach space when equipped with the norm
![]() $\Vert u\Vert _{W^{j,\infty }}+\sum _{|\unicode[STIX]{x1D6FE}|=j}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u|_{\ell }$
(see, e.g., [Reference Adams and Fournier1, Definition 1.29, p. 10]). Given
$\Vert u\Vert _{W^{j,\infty }}+\sum _{|\unicode[STIX]{x1D6FE}|=j}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u|_{\ell }$
(see, e.g., [Reference Adams and Fournier1, Definition 1.29, p. 10]). Given
![]() $j\in \mathbb{N}$
,
$j\in \mathbb{N}$
,
![]() $0<\ell <1$
and
$0<\ell <1$
and
![]() $s\in (\ell +j,\ell +j+N)$
, It follows that
$s\in (\ell +j,\ell +j+N)$
, It follows that
where
![]() $p(s)=\frac{N}{s-j-\ell }\in (1,\infty )$
. Indeed, we may assume
$p(s)=\frac{N}{s-j-\ell }\in (1,\infty )$
. Indeed, we may assume
![]() $j=0$
, as the general case follows by iteration. Suppose first
$j=0$
, as the general case follows by iteration. Suppose first
![]() $s\geqslant 1$
. Since
$s\geqslant 1$
. Since
![]() $s-\frac{N}{p(s)}=\ell =1-\frac{N}{p(1)}$
, it follows from [Reference Bergh and Löfström4, Theorem 6.5.1, p. 153] that
$s-\frac{N}{p(s)}=\ell =1-\frac{N}{p(1)}$
, it follows from [Reference Bergh and Löfström4, Theorem 6.5.1, p. 153] that
![]() $H^{s,p(s)}(\mathbb{R}^{N}){\hookrightarrow}H^{1,p(1)}(\mathbb{R}^{N})$
. The result now follows from the embedding
$H^{s,p(s)}(\mathbb{R}^{N}){\hookrightarrow}H^{1,p(1)}(\mathbb{R}^{N})$
. The result now follows from the embedding
![]() $H^{1,p(1)}(\mathbb{R}^{N}){\hookrightarrow}C^{0,\ell }(\overline{\mathbb{R}^{N}})$
(see [Reference Adams and Fournier1, Theorem 4.12 Part II, p. 85]). Let now
$H^{1,p(1)}(\mathbb{R}^{N}){\hookrightarrow}C^{0,\ell }(\overline{\mathbb{R}^{N}})$
(see [Reference Adams and Fournier1, Theorem 4.12 Part II, p. 85]). Let now
![]() $\ell <s<1$
, and note that
$\ell <s<1$
, and note that
![]() $H^{s,p(s)}(\mathbb{R}^{N}){\hookrightarrow}B_{\infty }^{s,p(s)}(\mathbb{R}^{N})$
(see [Reference Bergh and Löfström4, Theorem 6.2.4, p. 142]). Setting
$H^{s,p(s)}(\mathbb{R}^{N}){\hookrightarrow}B_{\infty }^{s,p(s)}(\mathbb{R}^{N})$
(see [Reference Bergh and Löfström4, Theorem 6.2.4, p. 142]). Setting
![]() $m=1$
, we have
$m=1$
, we have
![]() $m-1<\frac{N}{p(s)}<s<m$
, and the result follows from the embedding
$m-1<\frac{N}{p(s)}<s<m$
, and the result follows from the embedding
![]() $B_{\infty }^{s,p(s)}(\mathbb{R}^{N}){\hookrightarrow}C^{0,\ell }(\overline{\mathbb{R}^{N}})$
(see [Reference Adams and Fournier1, Theorem 7.37, p. 233]).
$B_{\infty }^{s,p(s)}(\mathbb{R}^{N}){\hookrightarrow}C^{0,\ell }(\overline{\mathbb{R}^{N}})$
(see [Reference Adams and Fournier1, Theorem 7.37, p. 233]).
We denote by
![]() $(e^{t\unicode[STIX]{x1D6E5}})_{t\geqslant 0}$
the heat semigroup on
$(e^{t\unicode[STIX]{x1D6E5}})_{t\geqslant 0}$
the heat semigroup on
![]() $\mathbb{R}^{N}$
, and we recall that
$\mathbb{R}^{N}$
, and we recall that
![]() $e^{t\unicode[STIX]{x1D6E5}}$
is a contraction on
$e^{t\unicode[STIX]{x1D6E5}}$
is a contraction on
![]() $L^{p}(\mathbb{R}^{N})$
for all
$L^{p}(\mathbb{R}^{N})$
for all
![]() $1\leqslant p\leqslant \infty$
. Using (1.13), it follows immediately that
$1\leqslant p\leqslant \infty$
. Using (1.13), it follows immediately that
![]() $(e^{t\unicode[STIX]{x1D6E5}})_{t\geqslant 0}$
is also a contraction semigroup on
$(e^{t\unicode[STIX]{x1D6E5}})_{t\geqslant 0}$
is also a contraction semigroup on
![]() $H^{s,p}(\mathbb{R}^{N})$
for all
$H^{s,p}(\mathbb{R}^{N})$
for all
![]() $s\geqslant 0$
and
$s\geqslant 0$
and
![]() $1<p<\infty$
.
$1<p<\infty$
.
2 Spatial singularities and ordinary differential equations
In this section, we study how a certain class of ODEs lead to loss of regularity. More precisely, we consider equations (1.9) and (1.10), which are ODEs with respect to time, as acting on functions depending on a space variable
![]() $|x|\leqslant 1$
. In particular, the initial value
$|x|\leqslant 1$
. In particular, the initial value
![]() $w(0,\cdot )=w_{0}(\cdot )$
is a function
$w(0,\cdot )=w_{0}(\cdot )$
is a function
![]() $w_{0}:[-1,1]\rightarrow \mathbb{C}$
. We wish to study the spatial regularity of
$w_{0}:[-1,1]\rightarrow \mathbb{C}$
. We wish to study the spatial regularity of
![]() $w(t,\cdot )$
as compared with the spatial regularity of
$w(t,\cdot )$
as compared with the spatial regularity of
![]() $w_{0}$
. This is a different phenomenon from finite-time blowup. For example, consider the ODE initial value problem
$w_{0}$
. This is a different phenomenon from finite-time blowup. For example, consider the ODE initial value problem
with
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}$
,
$\unicode[STIX]{x1D706}\in \mathbb{C}$
,
![]() $\unicode[STIX]{x1D706}\not =0$
and
$\unicode[STIX]{x1D706}\not =0$
and
![]() $|x|\leqslant 1$
. If
$|x|\leqslant 1$
. If
![]() $\Re \unicode[STIX]{x1D706}\not =0$
, then the solution of (2.1) is given by
$\Re \unicode[STIX]{x1D706}\not =0$
, then the solution of (2.1) is given by
It follows that
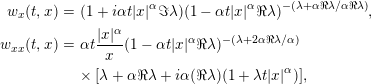 $$\begin{eqnarray}\displaystyle w_{x}(t,x) & = & \displaystyle (1+i\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706})(1-\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Re \unicode[STIX]{x1D706})^{-(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706})},\nonumber\\ \displaystyle w_{xx}(t,x) & = & \displaystyle \unicode[STIX]{x1D6FC}t\frac{|x|^{\unicode[STIX]{x1D6FC}}}{x}(1-\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Re \unicode[STIX]{x1D706})^{-(\unicode[STIX]{x1D706}+2\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FC})}\nonumber\\ \displaystyle & & \displaystyle \times \,[\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706}+i\unicode[STIX]{x1D6FC}(\Re \unicode[STIX]{x1D706})(1+\unicode[STIX]{x1D706}t|x|^{\unicode[STIX]{x1D6FC}})],\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w_{x}(t,x) & = & \displaystyle (1+i\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706})(1-\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Re \unicode[STIX]{x1D706})^{-(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706})},\nonumber\\ \displaystyle w_{xx}(t,x) & = & \displaystyle \unicode[STIX]{x1D6FC}t\frac{|x|^{\unicode[STIX]{x1D6FC}}}{x}(1-\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Re \unicode[STIX]{x1D706})^{-(\unicode[STIX]{x1D706}+2\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FC})}\nonumber\\ \displaystyle & & \displaystyle \times \,[\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FC}\Re \unicode[STIX]{x1D706}+i\unicode[STIX]{x1D6FC}(\Re \unicode[STIX]{x1D706})(1+\unicode[STIX]{x1D706}t|x|^{\unicode[STIX]{x1D6FC}})],\nonumber\end{eqnarray}$$
for
![]() $x\not =0$
, as long as these formulas make sense. If
$x\not =0$
, as long as these formulas make sense. If
![]() $\Re \unicode[STIX]{x1D706}=0$
, then the solution of (2.1) is given by
$\Re \unicode[STIX]{x1D706}=0$
, then the solution of (2.1) is given by
and so
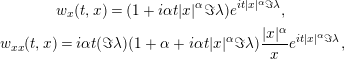 $$\begin{eqnarray}\displaystyle & \displaystyle w_{x}(t,x)=(1+i\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706})e^{it|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle w_{xx}(t,x)=i\unicode[STIX]{x1D6FC}t(\Im \unicode[STIX]{x1D706})(1+\unicode[STIX]{x1D6FC}+i\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706})\frac{|x|^{\unicode[STIX]{x1D6FC}}}{x}e^{it|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706}}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle w_{x}(t,x)=(1+i\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706})e^{it|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle w_{xx}(t,x)=i\unicode[STIX]{x1D6FC}t(\Im \unicode[STIX]{x1D706})(1+\unicode[STIX]{x1D6FC}+i\unicode[STIX]{x1D6FC}t|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706})\frac{|x|^{\unicode[STIX]{x1D6FC}}}{x}e^{it|x|^{\unicode[STIX]{x1D6FC}}\Im \unicode[STIX]{x1D706}}, & \displaystyle \nonumber\end{eqnarray}$$
for
![]() $t\geqslant 0$
and
$t\geqslant 0$
and
![]() $x\not =0$
. In both cases,
$x\not =0$
. In both cases,
![]() $w(t)$
is
$w(t)$
is
![]() $C^{1}$
in
$C^{1}$
in
![]() $[-1,1]$
as long as it exists. However, if
$[-1,1]$
as long as it exists. However, if
![]() $\unicode[STIX]{x1D6FC}<1$
, we see that
$\unicode[STIX]{x1D6FC}<1$
, we see that
![]() $w(t)$
fails to be twice differentiable at
$w(t)$
fails to be twice differentiable at
![]() $x=0$
, for
$x=0$
, for
![]() $t>0$
.
$t>0$
.
Somewhat surprisingly, it turns out that this loss of spatial regularity also occurs for regular perturbations of (2.1), as the following theorem shows.
Theorem 2.1. Let
![]() $0<\unicode[STIX]{x1D6FC}<1$
, let
$0<\unicode[STIX]{x1D6FC}<1$
, let
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
, let
$\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
, let
![]() $T>0$
, let
$T>0$
, let
![]() $w_{0}\in C^{2}([-1,1],\mathbb{C})$
, and let
$w_{0}\in C^{2}([-1,1],\mathbb{C})$
, and let
![]() $h\in C([0,T]\times [-1,1],\mathbb{C})$
, such that
$h\in C([0,T]\times [-1,1],\mathbb{C})$
, such that
![]() $\unicode[STIX]{x2202}_{y}h\in C([0,T]\times [-1,1],\mathbb{C})$
. Suppose further that
$\unicode[STIX]{x2202}_{y}h\in C([0,T]\times [-1,1],\mathbb{C})$
. Suppose further that
![]() $w_{0}(0)=0$
and
$w_{0}(0)=0$
and
![]() $h(t,0)=0$
for
$h(t,0)=0$
for
![]() $0\leqslant t\leqslant T$
. By possibly assuming that
$0\leqslant t\leqslant T$
. By possibly assuming that
![]() $T>0$
is smaller, it follows that there exists a solution
$T>0$
is smaller, it follows that there exists a solution
![]() $w\in C^{1}([0,T]\times [-1,1],\mathbb{C})$
of the equation
$w\in C^{1}([0,T]\times [-1,1],\mathbb{C})$
of the equation
If
![]() $w_{0}^{\prime }(0)\not =0$
and
$w_{0}^{\prime }(0)\not =0$
and
for some
![]() $0<\unicode[STIX]{x1D70F}\leqslant T$
and
$0<\unicode[STIX]{x1D70F}\leqslant T$
and
![]() $\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6FC}$
, then
$\unicode[STIX]{x1D6FD}>\unicode[STIX]{x1D6FC}$
, then
for all sufficiently small
![]() $t>0$
. In particular,
$t>0$
. In particular,
![]() $w(t,\cdot )$
is not twice differentiable at
$w(t,\cdot )$
is not twice differentiable at
![]() $y=0$
for any sufficiently small
$y=0$
for any sufficiently small
![]() $0<t\leqslant T$
.
$0<t\leqslant T$
.
Proof. The existence of the solution
![]() $w$
is straightforward, and
$w$
is straightforward, and
for all
![]() $0\leqslant t\leqslant T$
. For the rest of the proof, we consider for simplicity
$0\leqslant t\leqslant T$
. For the rest of the proof, we consider for simplicity
![]() $0\leqslant y\leqslant 1$
; the extension to
$0\leqslant y\leqslant 1$
; the extension to
![]() $-1\leqslant y\leqslant 0$
will be clear. Set
$-1\leqslant y\leqslant 0$
will be clear. Set
![]() $f(t,y)=\unicode[STIX]{x2202}_{y}h(t,y)$
and
$f(t,y)=\unicode[STIX]{x2202}_{y}h(t,y)$
and
![]() $v(t,y)=\unicode[STIX]{x2202}_{y}w(t,y)$
, so that
$v(t,y)=\unicode[STIX]{x2202}_{y}w(t,y)$
, so that
![]() $v,v_{t},f\in C([0,T]\times [0,1])$
. Differentiating equation (2.2) with respect to
$v,v_{t},f\in C([0,T]\times [0,1])$
. Differentiating equation (2.2) with respect to
![]() $y$
yields
$y$
yields
pointwise in
![]() $[0,T]\times [0,1]$
. Integrating (2.6) and setting
$[0,T]\times [0,1]$
. Integrating (2.6) and setting
we obtain
pointwise on
![]() $[0,T]\times [0,1]$
, where
$[0,T]\times [0,1]$
, where
We note that
![]() $A(t,0)=0$
by (2.5), so that
$A(t,0)=0$
by (2.5), so that
for all
![]() $0\leqslant t\leqslant T$
. Given
$0\leqslant t\leqslant T$
. Given
![]() $y>0$
, it follows from (2.8) and (2.10) that
$y>0$
, it follows from (2.8) and (2.10) that
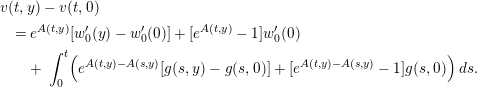 $$\begin{eqnarray}\displaystyle & & \displaystyle v(t,y)-v(t,0)\nonumber\\ \displaystyle & & \displaystyle \quad =e^{A(t,y)}[w_{0}^{\prime }(y)-w_{0}^{\prime }(0)]+[e^{A(t,y)}-1]w_{0}^{\prime }(0)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{t}\Bigl(e^{A(t,y)-A(s,y)}[g(s,y)-g(s,0)]+[e^{A(t,y)-A(s,y)}-1]g(s,0)\Bigr)\,ds.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle v(t,y)-v(t,0)\nonumber\\ \displaystyle & & \displaystyle \quad =e^{A(t,y)}[w_{0}^{\prime }(y)-w_{0}^{\prime }(0)]+[e^{A(t,y)}-1]w_{0}^{\prime }(0)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{0}^{t}\Bigl(e^{A(t,y)-A(s,y)}[g(s,y)-g(s,0)]+[e^{A(t,y)-A(s,y)}-1]g(s,0)\Bigr)\,ds.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Observe that, by assumption,
![]() $w_{0}(0)=0$
and
$w_{0}(0)=0$
and
Thus, for every
![]() $\unicode[STIX]{x1D700}\in (0,1)$
there exists
$\unicode[STIX]{x1D700}\in (0,1)$
there exists
![]() $0<\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})\leqslant \min \{T,\unicode[STIX]{x1D700}\}$
such that
$0<\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})\leqslant \min \{T,\unicode[STIX]{x1D700}\}$
such that
in the region
Estimates (2.5) and (2.13) yield
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Next, we observe that by (2.9), the inequality
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Next, we observe that by (2.9), the inequality
![]() $|\,|z_{1}|^{\unicode[STIX]{x1D6FC}}-|z_{2}|^{\unicode[STIX]{x1D6FC}}|\leqslant |z_{1}-z_{2}|^{\unicode[STIX]{x1D6FC}}$
and (2.15),
$|\,|z_{1}|^{\unicode[STIX]{x1D6FC}}-|z_{2}|^{\unicode[STIX]{x1D6FC}}|\leqslant |z_{1}-z_{2}|^{\unicode[STIX]{x1D6FC}}$
and (2.15),
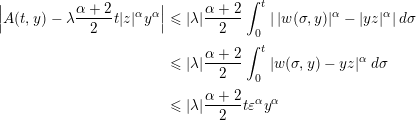 $$\begin{eqnarray}\displaystyle \Bigl|A(t,y)-\unicode[STIX]{x1D706}\frac{\unicode[STIX]{x1D6FC}+2}{2}t|z|^{\unicode[STIX]{x1D6FC}}y^{\unicode[STIX]{x1D6FC}}\Bigr| & {\leqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}\int _{0}^{t}|\,|w(\unicode[STIX]{x1D70E},y)|^{\unicode[STIX]{x1D6FC}}-|yz|^{\unicode[STIX]{x1D6FC}}|\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}\int _{0}^{t}|w(\unicode[STIX]{x1D70E},y)-yz|^{\unicode[STIX]{x1D6FC}}\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}t\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}}y^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Bigl|A(t,y)-\unicode[STIX]{x1D706}\frac{\unicode[STIX]{x1D6FC}+2}{2}t|z|^{\unicode[STIX]{x1D6FC}}y^{\unicode[STIX]{x1D6FC}}\Bigr| & {\leqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}\int _{0}^{t}|\,|w(\unicode[STIX]{x1D70E},y)|^{\unicode[STIX]{x1D6FC}}-|yz|^{\unicode[STIX]{x1D6FC}}|\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}\int _{0}^{t}|w(\unicode[STIX]{x1D70E},y)-yz|^{\unicode[STIX]{x1D6FC}}\,d\unicode[STIX]{x1D70E}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}t\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}}y^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. In particular,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. In particular,
![]() $A$
is bounded. Since
$A$
is bounded. Since
![]() $w_{0}$
is
$w_{0}$
is
![]() $C^{2}$
, it follows that
$C^{2}$
, it follows that
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Moreover,
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Moreover,
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
, where we use (2.16) in the last inequality. It follows from (2.18) and (2.16) that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
, where we use (2.16) in the last inequality. It follows from (2.18) and (2.16) that
Next, using again the boundedness of
![]() $A$
in
$A$
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
, we deduce from (2.3) that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
, we deduce from (2.3) that
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Using (2.16), we see that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Using (2.16), we see that
for
![]() $0<s<t$
and
$0<s<t$
and
![]() $(t,y)\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Moreover, it follows from (2.13) and (2.15) that
$(t,y)\in \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. Moreover, it follows from (2.13) and (2.15) that
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. We deduce from (2.7), (2.20), (2.21) and (2.22) that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. We deduce from (2.7), (2.20), (2.21) and (2.22) that
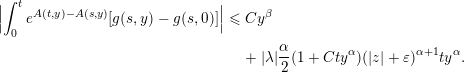 $$\begin{eqnarray}\displaystyle \Bigl|\int _{0}^{t}e^{A(t,y)-A(s,y)}[g(s,y)-g(s,0)]\Bigr| & {\leqslant} & \displaystyle Cy^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,|\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}}{2}(1+Cty^{\unicode[STIX]{x1D6FC}})(|z|+\unicode[STIX]{x1D700})^{\unicode[STIX]{x1D6FC}+1}ty^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Bigl|\int _{0}^{t}e^{A(t,y)-A(s,y)}[g(s,y)-g(s,0)]\Bigr| & {\leqslant} & \displaystyle Cy^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,|\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}}{2}(1+Cty^{\unicode[STIX]{x1D6FC}})(|z|+\unicode[STIX]{x1D700})^{\unicode[STIX]{x1D6FC}+1}ty^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
Next,
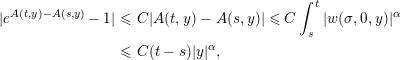 $$\begin{eqnarray}\displaystyle |e^{A(t,y)-A(s,y)}-1| & {\leqslant} & \displaystyle C|A(t,y)-A(s,y)|\leqslant C\int _{s}^{t}|w(\unicode[STIX]{x1D70E},0,y)|^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(t-s)|y|^{\unicode[STIX]{x1D6FC}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |e^{A(t,y)-A(s,y)}-1| & {\leqslant} & \displaystyle C|A(t,y)-A(s,y)|\leqslant C\int _{s}^{t}|w(\unicode[STIX]{x1D70E},0,y)|^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(t-s)|y|^{\unicode[STIX]{x1D6FC}},\nonumber\end{eqnarray}$$
where we use (2.15) in the last inequality. Since
![]() $g$
is bounded, it follows that
$g$
is bounded, it follows that
Finally, we observe that the various terms on the right-hand side of (2.11) are estimated by (2.17), (2.19), (2.23) and (2.24), and we deduce that
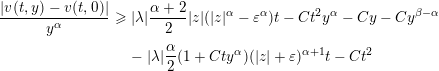 $$\begin{eqnarray}\displaystyle \frac{|v(t,y)-v(t,0)|}{y^{\unicode[STIX]{x1D6FC}}} & {\geqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}|z|(|z|^{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}})t-Ct^{2}y^{\unicode[STIX]{x1D6FC}}-Cy-Cy^{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle -\,|\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}}{2}(1+Cty^{\unicode[STIX]{x1D6FC}})(|z|+\unicode[STIX]{x1D700})^{\unicode[STIX]{x1D6FC}+1}t-Ct^{2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{|v(t,y)-v(t,0)|}{y^{\unicode[STIX]{x1D6FC}}} & {\geqslant} & \displaystyle |\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}+2}{2}|z|(|z|^{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}})t-Ct^{2}y^{\unicode[STIX]{x1D6FC}}-Cy-Cy^{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle -\,|\unicode[STIX]{x1D706}|\frac{\unicode[STIX]{x1D6FC}}{2}(1+Cty^{\unicode[STIX]{x1D6FC}})(|z|+\unicode[STIX]{x1D700})^{\unicode[STIX]{x1D6FC}+1}t-Ct^{2}\nonumber\end{eqnarray}$$
in
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. It follows that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D700}}$
. It follows that
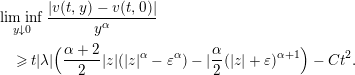 $$\begin{eqnarray}\displaystyle & & \displaystyle \liminf _{y\downarrow 0}\frac{|v(t,y)-v(t,0)|}{y^{\unicode[STIX]{x1D6FC}}}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant t|\unicode[STIX]{x1D706}|\Bigl(\frac{\unicode[STIX]{x1D6FC}+2}{2}|z|(|z|^{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}})-|\frac{\unicode[STIX]{x1D6FC}}{2}(|z|+\unicode[STIX]{x1D700})^{\unicode[STIX]{x1D6FC}+1}\Bigr)-Ct^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \liminf _{y\downarrow 0}\frac{|v(t,y)-v(t,0)|}{y^{\unicode[STIX]{x1D6FC}}}\nonumber\\ \displaystyle & & \displaystyle \quad \geqslant t|\unicode[STIX]{x1D706}|\Bigl(\frac{\unicode[STIX]{x1D6FC}+2}{2}|z|(|z|^{\unicode[STIX]{x1D6FC}}-\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}})-|\frac{\unicode[STIX]{x1D6FC}}{2}(|z|+\unicode[STIX]{x1D700})^{\unicode[STIX]{x1D6FC}+1}\Bigr)-Ct^{2}.\nonumber\end{eqnarray}$$
Choosing
![]() $\unicode[STIX]{x1D700}>0$
and
$\unicode[STIX]{x1D700}>0$
and
![]() $t>0$
sufficiently small, we see that
$t>0$
sufficiently small, we see that
from which estimate (2.4) follows.◻
Remark 2.2. The assumption that
![]() $w_{0}\in C^{2}([0,1],\mathbb{C})$
is used only once in the proof (see (2.17)). It could be replaced by the weaker condition
$w_{0}\in C^{2}([0,1],\mathbb{C})$
is used only once in the proof (see (2.17)). It could be replaced by the weaker condition
![]() $w_{0}\in C^{1,\unicode[STIX]{x1D707}}([0,1],\mathbb{C})$
with
$w_{0}\in C^{1,\unicode[STIX]{x1D707}}([0,1],\mathbb{C})$
with
![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D707}<1$
.
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D707}<1$
.
3 Semilinear equations as perturbations of an ordinary differential equation
In this section, we show that Theorem 2.1 easily implies Theorems 1.1 and 1.5.
Proof of Theorem 1.1.
We recall that if
![]() $\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
,
$\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
,
![]() $u_{0}\in C^{3}(\mathbb{R}^{N})\cap W^{3,\infty }(\mathbb{R}^{N})$
, and
$u_{0}\in C^{3}(\mathbb{R}^{N})\cap W^{3,\infty }(\mathbb{R}^{N})$
, and
![]() $|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u|_{\unicode[STIX]{x1D6FC}}<\infty$
for all multi-indices
$|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u|_{\unicode[STIX]{x1D6FC}}<\infty$
for all multi-indices
![]() $\unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}$
such that
![]() $|\unicode[STIX]{x1D6FE}|=3$
, then
$|\unicode[STIX]{x1D6FE}|=3$
, then
![]() $u$
is once continuously differentiable with respect to
$u$
is once continuously differentiable with respect to
![]() $t$
, three times continuously differentiable with respect to
$t$
, three times continuously differentiable with respect to
![]() $x$
,
$x$
,
![]() $u_{t}$
is
$u_{t}$
is
![]() $\frac{\unicode[STIX]{x1D6FC}}{2}$
-Hölder continuous in
$\frac{\unicode[STIX]{x1D6FC}}{2}$
-Hölder continuous in
![]() $t$
and
$t$
and
![]() $\sup _{0\leqslant t\leqslant T}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u(t)|_{\unicode[STIX]{x1D6FC}}<\infty$
for
$\sup _{0\leqslant t\leqslant T}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FE}}u(t)|_{\unicode[STIX]{x1D6FC}}<\infty$
for
![]() $|\unicode[STIX]{x1D6FE}|=3$
and
$|\unicode[STIX]{x1D6FE}|=3$
and
![]() $0<T<T_{\max }$
. See Theorem A.1 below for a precise statement. We write the variable in
$0<T<T_{\max }$
. See Theorem A.1 below for a precise statement. We write the variable in
![]() $\mathbb{R}^{N}$
in the form
$\mathbb{R}^{N}$
in the form
![]() $x=(x^{\prime },y)$
,
$x=(x^{\prime },y)$
,
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
,
$x^{\prime }\in \mathbb{R}^{N-1}$
,
![]() $y\in \mathbb{R}$
. Accordingly, we write
$y\in \mathbb{R}$
. Accordingly, we write
![]() $u_{0}(x)=u_{0}(x^{\prime },y)$
and
$u_{0}(x)=u_{0}(x^{\prime },y)$
and
![]() $u(t,x)=u(t,x^{\prime },y)$
.
$u(t,x)=u(t,x^{\prime },y)$
.
Let
![]() $u_{0}\in C_{0}(\mathbb{R}^{N})$
with
$u_{0}\in C_{0}(\mathbb{R}^{N})$
with
![]() $\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
. Suppose further that
$\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
. Suppose further that
![]() $u_{0}(x^{\prime },-y)=-u_{0}(x^{\prime },y)$
for all
$u_{0}(x^{\prime },-y)=-u_{0}(x^{\prime },y)$
for all
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
and
$x^{\prime }\in \mathbb{R}^{N-1}$
and
![]() $y\in \mathbb{R}$
, and
$y\in \mathbb{R}$
, and
![]() $\unicode[STIX]{x2202}_{y}u_{0}(0,0)\not =0$
. Note that
$\unicode[STIX]{x2202}_{y}u_{0}(0,0)\not =0$
. Note that
![]() $u$
inherits the anti-symmetry of the initial condition; that is,
$u$
inherits the anti-symmetry of the initial condition; that is,
![]() $u(t,x^{\prime },-y)\equiv -u(t,x^{\prime },y)$
for all
$u(t,x^{\prime },-y)\equiv -u(t,x^{\prime },y)$
for all
![]() $0<t<T_{\max }$
. Moreover, there exists
$0<t<T_{\max }$
. Moreover, there exists
![]() $0<t_{0}<T_{\max }$
such that
$0<t_{0}<T_{\max }$
such that
![]() $\unicode[STIX]{x2202}_{y}u(t,0,0)\not =0$
for all
$\unicode[STIX]{x2202}_{y}u(t,0,0)\not =0$
for all
![]() $0\leqslant t\leqslant t_{0}$
. Thus, we see that for all
$0\leqslant t\leqslant t_{0}$
. Thus, we see that for all
![]() $0\leqslant t\leqslant t_{0}$
,
$0\leqslant t\leqslant t_{0}$
,
![]() $u(t)$
satisfies the same assumptions as
$u(t)$
satisfies the same assumptions as
![]() $u_{0}$
. Therefore, it suffices to prove (1.8) for
$u_{0}$
. Therefore, it suffices to prove (1.8) for
![]() $s=0$
. Assume by contradiction that
$s=0$
. Assume by contradiction that
for some
![]() $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}\leqslant 1$
and
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FD}\leqslant 1$
and
![]() $0<T<t_{0}$
. We apply Theorem 2.1 with
$0<T<t_{0}$
. We apply Theorem 2.1 with
![]() $w(t,y)=u(t,0,y)$
and
$w(t,y)=u(t,0,y)$
and
![]() $h(t,y)=\unicode[STIX]{x1D6E5}u(t,0,y)$
. The anti-symmetry property of
$h(t,y)=\unicode[STIX]{x1D6E5}u(t,0,y)$
. The anti-symmetry property of
![]() $u$
implies that
$u$
implies that
![]() $w(t,0)=h(t,0)=0$
for all
$w(t,0)=h(t,0)=0$
for all
![]() $0\leqslant t<T_{\max }$
. Moreover, it follows from (3.1) that the assumption (2.3) is satisfied. Therefore, we deduce from (2.4) that if
$0\leqslant t<T_{\max }$
. Moreover, it follows from (3.1) that the assumption (2.3) is satisfied. Therefore, we deduce from (2.4) that if
![]() $t_{0}>0$
is sufficiently small, then
$t_{0}>0$
is sufficiently small, then
for
![]() $0<t<t_{0}$
. Since
$0<t<t_{0}$
. Since
![]() $\unicode[STIX]{x2202}_{y}w(t,y)=\unicode[STIX]{x2202}_{y}u(t,0,y)$
is
$\unicode[STIX]{x2202}_{y}w(t,y)=\unicode[STIX]{x2202}_{y}u(t,0,y)$
is
![]() $C^{1}$
in
$C^{1}$
in
![]() $y$
, this yields a contradiction. The result follows, since we can choose
$y$
, this yields a contradiction. The result follows, since we can choose
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
as above.◻
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
as above.◻
Remark 3.1. If
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}\setminus \{0\}$
, then the statement of Theorem 1.1 can be improved, in the sense that there exists an initial value
$\unicode[STIX]{x1D706}\in \mathbb{R}\setminus \{0\}$
, then the statement of Theorem 1.1 can be improved, in the sense that there exists an initial value
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
for which (1.8) holds for all
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
for which (1.8) holds for all
![]() $0\leqslant s<t<T_{\max }$
. (We do not require that
$0\leqslant s<t<T_{\max }$
. (We do not require that
![]() $t$
is small.) Indeed, let
$t$
is small.) Indeed, let
![]() $u_{0}\in C_{0}(\mathbb{R}^{N})$
with
$u_{0}\in C_{0}(\mathbb{R}^{N})$
with
![]() $\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
. Suppose further that
$\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
. Suppose further that
![]() $u_{0}(x^{\prime },-y)=-u_{0}(x^{\prime },y)$
for all
$u_{0}(x^{\prime },-y)=-u_{0}(x^{\prime },y)$
for all
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
and
$x^{\prime }\in \mathbb{R}^{N-1}$
and
![]() $y\in \mathbb{R}$
,
$y\in \mathbb{R}$
,
![]() $u_{0}(x^{\prime },y)\geqslant 0$
for all
$u_{0}(x^{\prime },y)\geqslant 0$
for all
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
and
$x^{\prime }\in \mathbb{R}^{N-1}$
and
![]() $y>0$
, and
$y>0$
, and
![]() $\unicode[STIX]{x2202}_{y}u_{0}(0,0)>0$
. Since
$\unicode[STIX]{x2202}_{y}u_{0}(0,0)>0$
. Since
![]() $u$
inherits the anti-symmetry of the initial condition, that is
$u$
inherits the anti-symmetry of the initial condition, that is
![]() $u(t,x^{\prime },-y)\equiv -u(t,x^{\prime },y)$
, it follows that, restricted to the open half space
$u(t,x^{\prime },-y)\equiv -u(t,x^{\prime },y)$
, it follows that, restricted to the open half space
![]() $\mathbb{R}_{+}^{N}=\mathbb{R}^{N-1}\times (0,\infty )$
,
$\mathbb{R}_{+}^{N}=\mathbb{R}^{N-1}\times (0,\infty )$
,
![]() $u$
is a solution of the Dirichlet initial value problem on
$u$
is a solution of the Dirichlet initial value problem on
![]() $\mathbb{R}_{+}^{N}$
. In particular,
$\mathbb{R}_{+}^{N}$
. In particular,
![]() $u(t,x^{\prime },y)>0$
for
$u(t,x^{\prime },y)>0$
for
![]() $y>0$
, and
$y>0$
, and
![]() $\unicode[STIX]{x2202}_{y}u(t,x^{\prime },0)>0$
. Thus, we see that for all
$\unicode[STIX]{x2202}_{y}u(t,x^{\prime },0)>0$
. Thus, we see that for all
![]() $0\leqslant t<T_{\max }$
,
$0\leqslant t<T_{\max }$
,
![]() $u(t)$
satisfies the same assumptions as
$u(t)$
satisfies the same assumptions as
![]() $u_{0}$
, and we can conclude as above.
$u_{0}$
, and we can conclude as above.
We turn next to Theorem 1.5. Equation (1.2) is a particular case of the following nonlinear complex Ginzburg–Landau equation:
in
![]() $\mathbb{R}^{N}$
, where
$\mathbb{R}^{N}$
, where
![]() $-\frac{\unicode[STIX]{x1D70B}}{2}\leqslant \unicode[STIX]{x1D703}\leqslant \frac{\unicode[STIX]{x1D70B}}{2}$
, and
$-\frac{\unicode[STIX]{x1D70B}}{2}\leqslant \unicode[STIX]{x1D703}\leqslant \frac{\unicode[STIX]{x1D70B}}{2}$
, and
![]() $0<\unicode[STIX]{x1D6FC}<1$
. Theorem 1.5 is therefore a consequence of the following result.
$0<\unicode[STIX]{x1D6FC}<1$
. Theorem 1.5 is therefore a consequence of the following result.
Theorem 3.2. Let
![]() $0<\unicode[STIX]{x1D706}<1$
, let
$0<\unicode[STIX]{x1D706}<1$
, let
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
, and let
$\unicode[STIX]{x1D706}\in \mathbb{C}\setminus \{0\}$
, and let
![]() $-\frac{\unicode[STIX]{x1D70B}}{2}\leqslant \unicode[STIX]{x1D703}\leqslant \frac{\unicode[STIX]{x1D70B}}{2}$
. Suppose that
$-\frac{\unicode[STIX]{x1D70B}}{2}\leqslant \unicode[STIX]{x1D703}\leqslant \frac{\unicode[STIX]{x1D70B}}{2}$
. Suppose that
![]() $s>3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
. There exists
$s>3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
. There exists
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that there is no
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
such that there is no
![]() $T>0$
for which there exists a solution
$T>0$
for which there exists a solution
![]() $u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (3.2).
$u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (3.2).
Remark 3.3.
-
(i) Suppose that
 $s>3+\frac{N}{2}$
(so that
$s>3+\frac{N}{2}$
(so that
 $H^{s}(\mathbb{R}^{N})\subset C^{3}(\mathbb{R}^{N})\cap W^{3,\infty }(\mathbb{R}^{N})$
). If
$H^{s}(\mathbb{R}^{N})\subset C^{3}(\mathbb{R}^{N})\cap W^{3,\infty }(\mathbb{R}^{N})$
). If
 $u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
, then and
$u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
, then and $$\begin{eqnarray}\unicode[STIX]{x1D6E5}u,|u|^{\unicode[STIX]{x1D6FC}}u\in C([0,T]\times \mathbb{R}^{N})\cap C([0,T],L^{2}(\mathbb{R}^{N}))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}u,|u|^{\unicode[STIX]{x1D6FC}}u\in C([0,T]\times \mathbb{R}^{N})\cap C([0,T],L^{2}(\mathbb{R}^{N}))\end{eqnarray}$$
 $\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D6E5}u,\unicode[STIX]{x1D6FB}(|u|^{\unicode[STIX]{x1D6FC}}u)\in C([0,T]\times \mathbb{R}^{N})$
. Therefore, equation (3.2) makes sense for such a
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D6E5}u,\unicode[STIX]{x1D6FB}(|u|^{\unicode[STIX]{x1D6FC}}u)\in C([0,T]\times \mathbb{R}^{N})$
. Therefore, equation (3.2) makes sense for such a
 $u$
. Furthermore, and
$u$
. Furthermore, and $$\begin{eqnarray}u_{t}\in C([0,T]\times \mathbb{R}^{N})\cap C([0,T],L^{2}(\mathbb{R}^{N}))\end{eqnarray}$$
$$\begin{eqnarray}u_{t}\in C([0,T]\times \mathbb{R}^{N})\cap C([0,T],L^{2}(\mathbb{R}^{N}))\end{eqnarray}$$
 $\unicode[STIX]{x1D6FB}u_{t}\in C([0,T]\times \mathbb{R}^{N})$
.
$\unicode[STIX]{x1D6FB}u_{t}\in C([0,T]\times \mathbb{R}^{N})$
.
-
(ii) It follows from the preceding observation that it makes sense to talk of a solution of (3.2) in
 $C([0,T],H^{s}(\mathbb{R}^{N}))$
if
$C([0,T],H^{s}(\mathbb{R}^{N}))$
if
 $s>3+\frac{N}{2}$
. Such a solution satisfies the integral equation Using the embedding
$s>3+\frac{N}{2}$
. Such a solution satisfies the integral equation Using the embedding $$\begin{eqnarray}u(t)=e^{it\unicode[STIX]{x1D6E5}}u_{0}+i\unicode[STIX]{x1D706}\int _{0}^{t}e^{i(t-s)\unicode[STIX]{x1D6E5}}(|u|^{\unicode[STIX]{x1D6FC}}u)(s)\,ds.\end{eqnarray}$$
$$\begin{eqnarray}u(t)=e^{it\unicode[STIX]{x1D6E5}}u_{0}+i\unicode[STIX]{x1D706}\int _{0}^{t}e^{i(t-s)\unicode[STIX]{x1D6E5}}(|u|^{\unicode[STIX]{x1D6FC}}u)(s)\,ds.\end{eqnarray}$$
 $H^{s}(\mathbb{R}^{N}){\hookrightarrow}L^{\infty }(\mathbb{R}^{N})$
, it follows easily that such a solution is unique. In particular, if
$H^{s}(\mathbb{R}^{N}){\hookrightarrow}L^{\infty }(\mathbb{R}^{N})$
, it follows easily that such a solution is unique. In particular, if
 $u_{0}$
is anti-symmetric in the last variable, then so is any solution
$u_{0}$
is anti-symmetric in the last variable, then so is any solution
 $u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (3.2).
$u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (3.2).
Proof of Theorem 3.2.
We write the variable in
![]() $\mathbb{R}^{N}$
in the form
$\mathbb{R}^{N}$
in the form
![]() $x=(x^{\prime },y)$
,
$x=(x^{\prime },y)$
,
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
,
$x^{\prime }\in \mathbb{R}^{N-1}$
,
![]() $y\in \mathbb{R}$
. Accordingly, we write
$y\in \mathbb{R}$
. Accordingly, we write
![]() $u_{0}(x)=u_{0}(x^{\prime },y)$
and
$u_{0}(x)=u_{0}(x^{\prime },y)$
and
![]() $u(t,x)=u(t,x^{\prime },y)$
.
$u(t,x)=u(t,x^{\prime },y)$
.
Let
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
, and suppose that
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
, and suppose that
![]() $u_{0}(x^{\prime },-y)=-u_{0}(x^{\prime },y)$
for all
$u_{0}(x^{\prime },-y)=-u_{0}(x^{\prime },y)$
for all
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
and
$x^{\prime }\in \mathbb{R}^{N-1}$
and
![]() $y\in \mathbb{R}$
, and
$y\in \mathbb{R}$
, and
![]() $\unicode[STIX]{x2202}_{y}u_{0}(0,0)>0$
. Assume by contradiction that there exist
$\unicode[STIX]{x2202}_{y}u_{0}(0,0)>0$
. Assume by contradiction that there exist
![]() $T>0$
,
$T>0$
,
![]() $s>3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
, and a solution
$s>3+\frac{N}{2}+\unicode[STIX]{x1D6FC}$
, and a solution
![]() $u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (3.2). As observed in Remark 3.3
(ii), it follows, in particular, that
$u\in C([0,T],H^{s}(\mathbb{R}^{N}))$
of (3.2). As observed in Remark 3.3
(ii), it follows, in particular, that
![]() $u(t,x^{\prime },-y)\equiv -u(t,x^{\prime },y)$
for all
$u(t,x^{\prime },-y)\equiv -u(t,x^{\prime },y)$
for all
![]() $0\leqslant t\leqslant T$
. We apply Theorem 2.1 with
$0\leqslant t\leqslant T$
. We apply Theorem 2.1 with
![]() $w(t,y)=u(t,0,y)$
and
$w(t,y)=u(t,0,y)$
and
![]() $h(t,y)=e^{i\unicode[STIX]{x1D703}}\unicode[STIX]{x1D6E5}u(t,0,y)$
. The regularity assumptions on
$h(t,y)=e^{i\unicode[STIX]{x1D703}}\unicode[STIX]{x1D6E5}u(t,0,y)$
. The regularity assumptions on
![]() $w$
and
$w$
and
![]() $h$
are satisfied by Remark 3.3
(i). The anti-symmetry property of
$h$
are satisfied by Remark 3.3
(i). The anti-symmetry property of
![]() $u$
implies that
$u$
implies that
![]() $w(t,0)=h(t,0)=0$
for all
$w(t,0)=h(t,0)=0$
for all
![]() $0\leqslant t<T_{\max }$
. Moreover, it follows from Sobolev’s embedding theorem (see (1.15)) that
$0\leqslant t<T_{\max }$
. Moreover, it follows from Sobolev’s embedding theorem (see (1.15)) that
for all
![]() $t\in [0,T]$
and
$t\in [0,T]$
and
![]() $y\in \mathbb{R}$
, so that the assumption (2.3) is satisfied. Therefore, we deduce from (2.4) that if
$y\in \mathbb{R}$
, so that the assumption (2.3) is satisfied. Therefore, we deduce from (2.4) that if
![]() $t_{0}>0$
is sufficiently small, then
$t_{0}>0$
is sufficiently small, then
for
![]() $0<t<t_{0}$
. Since
$0<t<t_{0}$
. Since
![]() $v(t,y)=\unicode[STIX]{x2202}_{y}u(t,0,y)$
is
$v(t,y)=\unicode[STIX]{x2202}_{y}u(t,0,y)$
is
![]() $C^{1}$
in
$C^{1}$
in
![]() $y$
by Remark 3.3
(i), this yields a contradiction.◻
$y$
by Remark 3.3
(i), this yields a contradiction.◻
4 Time-pointwise lack of regularity: the heat equation
In this section, we prove Theorems 1.7 and 1.10. As motivation for the proof of Theorem 1.7, consider an initial value
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
that is odd with respect to the
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
that is odd with respect to the
![]() $N$
th variable
$N$
th variable
![]() $y$
and such that
$y$
and such that
![]() $u_{0}(x^{\prime },y)=C(x^{\prime })y$
for small
$u_{0}(x^{\prime },y)=C(x^{\prime })y$
for small
![]() $|y|$
, and write
$|y|$
, and write
![]() $|u(t,x^{\prime },y)|^{\unicode[STIX]{x1D6FC}}u(t,x^{\prime },y)=C(x^{\prime })\unicode[STIX]{x1D6FE}(t)|y|^{\unicode[STIX]{x1D6FC}}y+\widetilde{w}(t,x^{\prime },y)$
, where
$|u(t,x^{\prime },y)|^{\unicode[STIX]{x1D6FC}}u(t,x^{\prime },y)=C(x^{\prime })\unicode[STIX]{x1D6FE}(t)|y|^{\unicode[STIX]{x1D6FC}}y+\widetilde{w}(t,x^{\prime },y)$
, where
![]() $|\widetilde{w}(t,x^{\prime },y)|\leqslant C|y|^{\unicode[STIX]{x1D6FC}+2}$
. This decomposition makes it possible to explicitly calculate
$|\widetilde{w}(t,x^{\prime },y)|\leqslant C|y|^{\unicode[STIX]{x1D6FC}+2}$
. This decomposition makes it possible to explicitly calculate
![]() $\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x1D6E5}}|u|^{\unicode[STIX]{x1D6FC}}u]_{y=0}$
. Incorporating this result into the integral (1.11) yields the desired property.
$\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x1D6E5}}|u|^{\unicode[STIX]{x1D6FC}}u]_{y=0}$
. Incorporating this result into the integral (1.11) yields the desired property.
The following two lemmas show explicitly how these ideas are implemented.
Lemma 4.1. Let
![]() $\unicode[STIX]{x1D713}\in C(\mathbb{R})$
, such that
$\unicode[STIX]{x1D713}\in C(\mathbb{R})$
, such that
![]() $|\unicode[STIX]{x1D713}(x)|\leqslant C(1+|x|^{m})$
for some
$|\unicode[STIX]{x1D713}(x)|\leqslant C(1+|x|^{m})$
for some
![]() $m\geqslant 0$
. Let
$m\geqslant 0$
. Let
![]() $\unicode[STIX]{x1D70E}>0$
, and set
$\unicode[STIX]{x1D70E}>0$
, and set
It follows that
Proof. We have
so that
We next calculate
so that
Thus, we deduce from (4.3) that
from which (4.2) follows.◻
Lemma 4.2. If
![]() $\unicode[STIX]{x1D713}(x)=|x|^{\unicode[STIX]{x1D6FC}}x$
with
$\unicode[STIX]{x1D713}(x)=|x|^{\unicode[STIX]{x1D6FC}}x$
with
![]() $\unicode[STIX]{x1D6FC}>0$
, then
$\unicode[STIX]{x1D6FC}>0$
, then
for all
![]() $\unicode[STIX]{x1D70E}>0$
, where
$\unicode[STIX]{x1D70E}>0$
, where
Proof. Considering (4.2), we must calculate
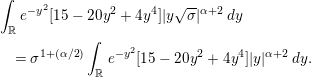 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}}e^{-y^{2}}[15-20y^{2}+4y^{4}]|y\sqrt{\unicode[STIX]{x1D70E}}|^{\unicode[STIX]{x1D6FC}+2}\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70E}^{1+(\unicode[STIX]{x1D6FC}/2)}\int _{\mathbb{R}}e^{-y^{2}}[15-20y^{2}+4y^{4}]|y|^{\unicode[STIX]{x1D6FC}+2}\,dy.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}}e^{-y^{2}}[15-20y^{2}+4y^{4}]|y\sqrt{\unicode[STIX]{x1D70E}}|^{\unicode[STIX]{x1D6FC}+2}\,dy\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70E}^{1+(\unicode[STIX]{x1D6FC}/2)}\int _{\mathbb{R}}e^{-y^{2}}[15-20y^{2}+4y^{4}]|y|^{\unicode[STIX]{x1D6FC}+2}\,dy.\end{eqnarray}$$
Note that, given any
![]() $\unicode[STIX]{x1D6FD}\geqslant 0$
,
$\unicode[STIX]{x1D6FD}\geqslant 0$
,
It follows that
and
Therefore,
Proof of Theorem 1.7.
We write the variable in
![]() $\mathbb{R}^{N}$
in the form
$\mathbb{R}^{N}$
in the form
![]() $x=(x^{\prime },y)$
,
$x=(x^{\prime },y)$
,
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
,
$x^{\prime }\in \mathbb{R}^{N-1}$
,
![]() $y\in \mathbb{R}$
. Accordingly, we write
$y\in \mathbb{R}$
. Accordingly, we write
![]() $u_{0}(x)=u_{0}(x^{\prime },y)$
and
$u_{0}(x)=u_{0}(x^{\prime },y)$
and
![]() $u(t,x)=u(t,x^{\prime },y)$
. We note that
$u(t,x)=u(t,x^{\prime },y)$
. We note that
where
![]() $e^{t\unicode[STIX]{x1D6E5}_{x^{\prime }}}$
is the convolution in
$e^{t\unicode[STIX]{x1D6E5}_{x^{\prime }}}$
is the convolution in
![]() $\mathbb{R}^{N-1}$
with the kernel
$\mathbb{R}^{N-1}$
with the kernel
![]() $(4\unicode[STIX]{x1D70B}t)^{-\frac{N-1}{2}}e^{-\frac{|x^{\prime }|^{2}}{4t}}$
, and
$(4\unicode[STIX]{x1D70B}t)^{-\frac{N-1}{2}}e^{-\frac{|x^{\prime }|^{2}}{4t}}$
, and
![]() $e^{t\unicode[STIX]{x2202}_{y}^{2}}$
is the convolution in
$e^{t\unicode[STIX]{x2202}_{y}^{2}}$
is the convolution in
![]() $\mathbb{R}$
with the kernel
$\mathbb{R}$
with the kernel
![]() $(4\unicode[STIX]{x1D70B}t)^{-\frac{1}{2}}e^{-\frac{y^{2}}{4t}}$
.
$(4\unicode[STIX]{x1D70B}t)^{-\frac{1}{2}}e^{-\frac{y^{2}}{4t}}$
.
Let
![]() $u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
, and let
$u_{0}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
, and let
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R})\cap L^{1}(\mathbb{R}^{N}))$
be the corresponding maximal solution of (1.1). Assume that
$u\in C([0,T_{\max }),C_{0}(\mathbb{R})\cap L^{1}(\mathbb{R}^{N}))$
be the corresponding maximal solution of (1.1). Assume that
Recall that
![]() $u$
is
$u$
is
![]() $C^{1}$
in time and
$C^{1}$
in time and
![]() $C^{3}$
in space, and that
$C^{3}$
in space, and that
for all
![]() $0<T<T_{\max }$
(see, e.g., Theorem A.1). Under the assumption (4.11), it follows that for all
$0<T<T_{\max }$
(see, e.g., Theorem A.1). Under the assumption (4.11), it follows that for all
![]() $0\leqslant t\leqslant T$
and
$0\leqslant t\leqslant T$
and
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
,
$x^{\prime }\in \mathbb{R}^{N-1}$
,
![]() $u(t,x^{\prime },\cdot )$
is odd and
$u(t,x^{\prime },\cdot )$
is odd and
![]() $u(t,x^{\prime },y)>0$
for
$u(t,x^{\prime },y)>0$
for
![]() $y>0$
. Moreover, if we set
$y>0$
. Moreover, if we set
then
![]() $\unicode[STIX]{x1D702}\in C([0,T_{\max })\times \mathbb{R}^{N-1})$
. Therefore, it follows from (4.11) that for every
$\unicode[STIX]{x1D702}\in C([0,T_{\max })\times \mathbb{R}^{N-1})$
. Therefore, it follows from (4.11) that for every
![]() $0<\unicode[STIX]{x1D700}<1$
there exists
$0<\unicode[STIX]{x1D700}<1$
there exists
![]() $0<\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}<T_{\max }$
such that
$0<\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}<T_{\max }$
such that
Let
![]() $w$
be defined by
$w$
be defined by
We claim that
for all
![]() $s\in [0,T]$
,
$s\in [0,T]$
,
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
and
$x^{\prime }\in \mathbb{R}^{N-1}$
and
![]() $y\in \mathbb{R}$
, where
$y\in \mathbb{R}$
, where
![]() $C=\frac{1}{2}\sup _{0\leqslant t\leqslant T}\Vert u(t)\Vert _{W^{2,\infty }}$
. Indeed, fix
$C=\frac{1}{2}\sup _{0\leqslant t\leqslant T}\Vert u(t)\Vert _{W^{2,\infty }}$
. Indeed, fix
![]() $0\leqslant s\leqslant T$
and
$0\leqslant s\leqslant T$
and
![]() $x^{\prime }\in \mathbb{R}^{N-1}$
, and set
$x^{\prime }\in \mathbb{R}^{N-1}$
, and set
We have
![]() $h^{\prime }(y)=\unicode[STIX]{x2202}_{y}u(s,x^{\prime },y)-\unicode[STIX]{x1D702}(s,x^{\prime })$
and
$h^{\prime }(y)=\unicode[STIX]{x2202}_{y}u(s,x^{\prime },y)-\unicode[STIX]{x1D702}(s,x^{\prime })$
and
![]() $h^{\prime \prime }(y)=\unicode[STIX]{x2202}_{y}^{2}u(s,x^{\prime },y)$
. In particular,
$h^{\prime \prime }(y)=\unicode[STIX]{x2202}_{y}^{2}u(s,x^{\prime },y)$
. In particular,
![]() $h(0)=h^{\prime }(0)=0$
, so that
$h(0)=h^{\prime }(0)=0$
, so that
and so
which proves (4.16). Since
![]() $u$
is bounded, we deduce easily from (4.15)–(4.16) that
$u$
is bounded, we deduce easily from (4.15)–(4.16) that
with
for all
![]() $s\in [0,T]$
and
$s\in [0,T]$
and
![]() $(x^{\prime },y)\in \mathbb{R}^{N}$
. It follows from Lemma 4.2 that if
$(x^{\prime },y)\in \mathbb{R}^{N}$
. It follows from Lemma 4.2 that if
![]() $\unicode[STIX]{x1D713}(y)=|y|^{\unicode[STIX]{x1D6FC}}y$
, then
$\unicode[STIX]{x1D713}(y)=|y|^{\unicode[STIX]{x1D6FC}}y$
, then
for all
![]() $\unicode[STIX]{x1D70E}>0$
, where
$\unicode[STIX]{x1D70E}>0$
, where
![]() $C_{\unicode[STIX]{x1D6FC}}>0$
is given by (4.7). We deduce from (4.10) and (4.19) that
$C_{\unicode[STIX]{x1D6FC}}>0$
is given by (4.7). We deduce from (4.10) and (4.19) that
On the other hand, it follows from (4.14) that there exists
![]() $C$
independent of
$C$
independent of
![]() $0<\unicode[STIX]{x1D700}<1$
such that
$0<\unicode[STIX]{x1D700}<1$
such that
By possibly choosing
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}>0$
smaller, we deduce that
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}>0$
smaller, we deduce that
It follows from (4.20) and (4.21) that
for all
![]() $0\leqslant s<t\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
$0\leqslant s<t\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
![]() $|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. On the other hand, it follows from (4.2) that
$|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. On the other hand, it follows from (4.2) that
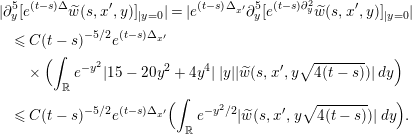 $$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x1D6E5}}\widetilde{w}(s,x^{\prime },y)]_{|y=0}|=|e^{(t-s)\unicode[STIX]{x1D6E5}_{x^{\prime }}}\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x2202}_{y}^{2}}\widetilde{w}(s,x^{\prime },y)]_{|y=0}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(t-s)^{-5/2}e^{(t-s)\unicode[STIX]{x1D6E5}_{x^{\prime }}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Bigl(\int _{\mathbb{R}}e^{-y^{2}}|15-20y^{2}+4y^{4}|\,|y||\widetilde{w}(s,x^{\prime },y\sqrt{4(t-s)})|\,dy\Bigr)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(t-s)^{-5/2}e^{(t-s)\unicode[STIX]{x1D6E5}_{x^{\prime }}}\Bigl(\int _{\mathbb{R}}e^{-y^{2}/2}|\widetilde{w}(s,x^{\prime },y\sqrt{4(t-s)})|\,dy\Bigr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x1D6E5}}\widetilde{w}(s,x^{\prime },y)]_{|y=0}|=|e^{(t-s)\unicode[STIX]{x1D6E5}_{x^{\prime }}}\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x2202}_{y}^{2}}\widetilde{w}(s,x^{\prime },y)]_{|y=0}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(t-s)^{-5/2}e^{(t-s)\unicode[STIX]{x1D6E5}_{x^{\prime }}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Bigl(\int _{\mathbb{R}}e^{-y^{2}}|15-20y^{2}+4y^{4}|\,|y||\widetilde{w}(s,x^{\prime },y\sqrt{4(t-s)})|\,dy\Bigr)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(t-s)^{-5/2}e^{(t-s)\unicode[STIX]{x1D6E5}_{x^{\prime }}}\Bigl(\int _{\mathbb{R}}e^{-y^{2}/2}|\widetilde{w}(s,x^{\prime },y\sqrt{4(t-s)})|\,dy\Bigr).\nonumber\end{eqnarray}$$
Applying (4.18), we deduce that
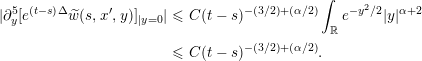 $$\begin{eqnarray}\displaystyle |\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x1D6E5}}\widetilde{w}(s,x^{\prime },y)]_{|y=0}| & {\leqslant} & \displaystyle C(t-s)^{-(3/2)+(\unicode[STIX]{x1D6FC}/2)}\int _{\mathbb{R}}e^{-y^{2}/2}|y|^{\unicode[STIX]{x1D6FC}+2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(t-s)^{-(3/2)+(\unicode[STIX]{x1D6FC}/2)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x2202}_{y}^{5}[e^{(t-s)\unicode[STIX]{x1D6E5}}\widetilde{w}(s,x^{\prime },y)]_{|y=0}| & {\leqslant} & \displaystyle C(t-s)^{-(3/2)+(\unicode[STIX]{x1D6FC}/2)}\int _{\mathbb{R}}e^{-y^{2}/2}|y|^{\unicode[STIX]{x1D6FC}+2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(t-s)^{-(3/2)+(\unicode[STIX]{x1D6FC}/2)}.\end{eqnarray}$$
It now follows from (4.17), (4.22) and (4.23) that
for all
![]() $0\leqslant s<t\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
$0\leqslant s<t\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
![]() $|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
.
$|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
.
The point is that
![]() $(t-s)^{-2+\frac{\unicode[STIX]{x1D6FC}}{2}}$
is not integrable in
$(t-s)^{-2+\frac{\unicode[STIX]{x1D6FC}}{2}}$
is not integrable in
![]() $s$
at
$s$
at
![]() $s=t$
under the assumption
$s=t$
under the assumption
![]() $0<\unicode[STIX]{x1D6FC}<2$
. We now conclude the proof as follows. Fix
$0<\unicode[STIX]{x1D6FC}<2$
. We now conclude the proof as follows. Fix
![]() $0<\unicode[STIX]{x1D70F}<T_{\max }$
and, given any
$0<\unicode[STIX]{x1D70F}<T_{\max }$
and, given any
![]() $0\leqslant t<\unicode[STIX]{x1D70F}$
, set
$0\leqslant t<\unicode[STIX]{x1D70F}$
, set
Since
![]() $\unicode[STIX]{x1D70F}-s\geqslant \unicode[STIX]{x1D70F}-t>0$
for
$\unicode[STIX]{x1D70F}-s\geqslant \unicode[STIX]{x1D70F}-t>0$
for
![]() $s\in [0,t]$
, the smoothing effect of the heat semigroup implies that the integrand in (4.25) is integrable as a function with values in
$s\in [0,t]$
, the smoothing effect of the heat semigroup implies that the integrand in (4.25) is integrable as a function with values in
![]() $H^{m}(\mathbb{R}^{N})$
for all
$H^{m}(\mathbb{R}^{N})$
for all
![]() $m\geqslant 0$
. Choosing
$m\geqslant 0$
. Choosing
![]() $m$
large enough so that
$m$
large enough so that
![]() $H^{m}(\mathbb{R}^{N})\subset C^{5}(\mathbb{R}^{N})$
, we see that the formula
$H^{m}(\mathbb{R}^{N})\subset C^{5}(\mathbb{R}^{N})$
, we see that the formula
makes sense. Applying (4.24) with
![]() $t$
replaced by
$t$
replaced by
![]() $\unicode[STIX]{x1D70F}$
, we deduce that
$\unicode[STIX]{x1D70F}$
, we deduce that
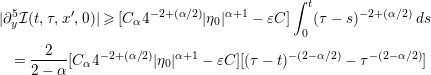 $$\begin{eqnarray}\displaystyle & & \displaystyle \quad |\unicode[STIX]{x2202}_{y}^{5}{\mathcal{I}}(t,\unicode[STIX]{x1D70F},x^{\prime },0)|\geqslant [C_{\unicode[STIX]{x1D6FC}}4^{-2+(\unicode[STIX]{x1D6FC}/2)}|\unicode[STIX]{x1D702}_{0}|^{\unicode[STIX]{x1D6FC}+1}-\unicode[STIX]{x1D700}C]\int _{0}^{t}(\unicode[STIX]{x1D70F}-s)^{-2+(\unicode[STIX]{x1D6FC}/2)}\,ds\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{2}{2-\unicode[STIX]{x1D6FC}}[C_{\unicode[STIX]{x1D6FC}}4^{-2+(\unicode[STIX]{x1D6FC}/2)}|\unicode[STIX]{x1D702}_{0}|^{\unicode[STIX]{x1D6FC}+1}-\unicode[STIX]{x1D700}C][(\unicode[STIX]{x1D70F}-t)^{-(2-\unicode[STIX]{x1D6FC}/2)}-\unicode[STIX]{x1D70F}^{-(2-\unicode[STIX]{x1D6FC}/2)}]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \quad |\unicode[STIX]{x2202}_{y}^{5}{\mathcal{I}}(t,\unicode[STIX]{x1D70F},x^{\prime },0)|\geqslant [C_{\unicode[STIX]{x1D6FC}}4^{-2+(\unicode[STIX]{x1D6FC}/2)}|\unicode[STIX]{x1D702}_{0}|^{\unicode[STIX]{x1D6FC}+1}-\unicode[STIX]{x1D700}C]\int _{0}^{t}(\unicode[STIX]{x1D70F}-s)^{-2+(\unicode[STIX]{x1D6FC}/2)}\,ds\nonumber\\ \displaystyle & & \displaystyle \qquad =\frac{2}{2-\unicode[STIX]{x1D6FC}}[C_{\unicode[STIX]{x1D6FC}}4^{-2+(\unicode[STIX]{x1D6FC}/2)}|\unicode[STIX]{x1D702}_{0}|^{\unicode[STIX]{x1D6FC}+1}-\unicode[STIX]{x1D700}C][(\unicode[STIX]{x1D70F}-t)^{-(2-\unicode[STIX]{x1D6FC}/2)}-\unicode[STIX]{x1D70F}^{-(2-\unicode[STIX]{x1D6FC}/2)}]\end{eqnarray}$$
for
![]() $0<t<\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
$0<t<\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
![]() $|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. We now fix
$|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. We now fix
![]() $s,p$
such that
$s,p$
such that
![]() $s\geqslant 5+\frac{1}{p}$
and
$s\geqslant 5+\frac{1}{p}$
and
![]() $\unicode[STIX]{x1D700}$
sufficiently small so that
$\unicode[STIX]{x1D700}$
sufficiently small so that
![]() $C_{\unicode[STIX]{x1D6FC}}4^{-2+\frac{\unicode[STIX]{x1D6FC}}{2}}|\unicode[STIX]{x1D702}_{0}|^{\unicode[STIX]{x1D6FC}+1}>\unicode[STIX]{x1D700}C$
, and we deduce from (4.27) and the embedding
$C_{\unicode[STIX]{x1D6FC}}4^{-2+\frac{\unicode[STIX]{x1D6FC}}{2}}|\unicode[STIX]{x1D702}_{0}|^{\unicode[STIX]{x1D6FC}+1}>\unicode[STIX]{x1D700}C$
, and we deduce from (4.27) and the embedding
![]() $H^{s,p}(\mathbb{R}){\hookrightarrow}W^{5,\infty }(\mathbb{R})$
that
$H^{s,p}(\mathbb{R}){\hookrightarrow}W^{5,\infty }(\mathbb{R})$
that
for some constants
![]() $a,A>0$
independent of
$a,A>0$
independent of
![]() $0<t<\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
$0<t<\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and
![]() $|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. We now use the property
$|x^{\prime }|\leqslant \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. We now use the property
(see (1.14)), and we deduce from (4.28) that for some constant
![]() $\unicode[STIX]{x1D708}>0$
$\unicode[STIX]{x1D708}>0$
so that
Observe that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}{\mathcal{I}}(t,\unicode[STIX]{x1D70F},x^{\prime },y) & = & \displaystyle \unicode[STIX]{x1D706}e^{(\unicode[STIX]{x1D70F}-t)\unicode[STIX]{x1D6E5}}\int _{0}^{t}e^{(t-s)\unicode[STIX]{x1D6E5}}|u(s)|^{\unicode[STIX]{x1D6FC}}u(s)\,ds\nonumber\\ \displaystyle & = & \displaystyle e^{(\unicode[STIX]{x1D70F}-t)\unicode[STIX]{x1D6E5}}[u(t)-e^{t\unicode[STIX]{x1D6E5}}u_{0}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}{\mathcal{I}}(t,\unicode[STIX]{x1D70F},x^{\prime },y) & = & \displaystyle \unicode[STIX]{x1D706}e^{(\unicode[STIX]{x1D70F}-t)\unicode[STIX]{x1D6E5}}\int _{0}^{t}e^{(t-s)\unicode[STIX]{x1D6E5}}|u(s)|^{\unicode[STIX]{x1D6FC}}u(s)\,ds\nonumber\\ \displaystyle & = & \displaystyle e^{(\unicode[STIX]{x1D70F}-t)\unicode[STIX]{x1D6E5}}[u(t)-e^{t\unicode[STIX]{x1D6E5}}u_{0}].\nonumber\end{eqnarray}$$
Hence,
Note that
![]() $\Vert u_{0}\Vert _{H^{s,p}}<\infty$
. Therefore, letting
$\Vert u_{0}\Vert _{H^{s,p}}<\infty$
. Therefore, letting
![]() $\unicode[STIX]{x1D70F}\downarrow t$
and applying (4.30), we conclude that
$\unicode[STIX]{x1D70F}\downarrow t$
and applying (4.30), we conclude that
![]() $\Vert u(t)\Vert _{H^{s,p}}=\infty$
.◻
$\Vert u(t)\Vert _{H^{s,p}}=\infty$
.◻
Remark 4.3. Observe that if
![]() $u_{0}$
is as in the proof of Theorem 1.7, then so is
$u_{0}$
is as in the proof of Theorem 1.7, then so is
![]() $\unicode[STIX]{x1D700}u_{0}$
for all
$\unicode[STIX]{x1D700}u_{0}$
for all
![]() $\unicode[STIX]{x1D700}\not =0$
.
$\unicode[STIX]{x1D700}\not =0$
.
Remark 4.4. A careful analysis of the proof of Theorem 1.7 shows that the property
![]() $C_{\unicode[STIX]{x1D6FC}}>0$
(i.e.,
$C_{\unicode[STIX]{x1D6FC}}>0$
(i.e.,
![]() $\unicode[STIX]{x1D6FC}<2$
), where
$\unicode[STIX]{x1D6FC}<2$
), where
![]() $C_{\unicode[STIX]{x1D6FC}}$
is given by (4.7), could, in principle, be replaced by the condition
$C_{\unicode[STIX]{x1D6FC}}$
is given by (4.7), could, in principle, be replaced by the condition
![]() $C_{\unicode[STIX]{x1D6FC}}\not =0$
(i.e.,
$C_{\unicode[STIX]{x1D6FC}}\not =0$
(i.e.,
![]() $\unicode[STIX]{x1D6FC}\not =2$
). On the other hand, the condition
$\unicode[STIX]{x1D6FC}\not =2$
). On the other hand, the condition
![]() $\unicode[STIX]{x1D6FC}<2$
is crucial in proving (4.30) by letting
$\unicode[STIX]{x1D6FC}<2$
is crucial in proving (4.30) by letting
![]() $\unicode[STIX]{x1D70F}\downarrow t$
in (4.29).
$\unicode[STIX]{x1D70F}\downarrow t$
in (4.29).
Proof of Theorem 1.10.
We argue by contradiction. Suppose that for some
![]() $s\geqslant 0$
the Cauchy problem (1.1) is locally well-posed for small data in
$s\geqslant 0$
the Cauchy problem (1.1) is locally well-posed for small data in
![]() $H^{s}(\mathbb{R}^{N})$
. Using Theorem 1.7 and Remark 4.3 with
$H^{s}(\mathbb{R}^{N})$
. Using Theorem 1.7 and Remark 4.3 with
![]() $p=2$
, we see that
$p=2$
, we see that
![]() $2s\leqslant 11$
. It follows then from (1.12) that
$2s\leqslant 11$
. It follows then from (1.12) that
A scaling argument allows us now to conclude. Indeed, let
![]() $\unicode[STIX]{x1D711}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
,
$\unicode[STIX]{x1D711}\in C_{\text{c}}^{\infty }(\mathbb{R}^{N})$
,
![]() $\unicode[STIX]{x1D711}\not =0$
. Since
$\unicode[STIX]{x1D711}\not =0$
. Since
![]() $\unicode[STIX]{x1D706}>0$
, for
$\unicode[STIX]{x1D706}>0$
, for
![]() $k>0$
sufficiently large, the (classical) solution
$k>0$
sufficiently large, the (classical) solution
![]() $u$
of (1.1) with initial value
$u$
of (1.1) with initial value
![]() $u_{0}=k\unicode[STIX]{x1D711}$
blows up in finite time, say at
$u_{0}=k\unicode[STIX]{x1D711}$
blows up in finite time, say at
![]() $T_{\max }$
. Given
$T_{\max }$
. Given
![]() $\unicode[STIX]{x1D707}>0$
, let
$\unicode[STIX]{x1D707}>0$
, let
It follows that
![]() $u_{\unicode[STIX]{x1D707}}$
is a solution of (1.1) with the initial value
$u_{\unicode[STIX]{x1D707}}$
is a solution of (1.1) with the initial value
which blows up at
On the other hand,
for
![]() $\unicode[STIX]{x1D707}\geqslant 1$
. Using (4.31), we see that
$\unicode[STIX]{x1D707}\geqslant 1$
. Using (4.31), we see that
Comparing (4.36) and (4.34), we conclude that (1.1) cannot be locally well-posed for small data in
![]() $H^{s}(\mathbb{R}^{N})$
.◻
$H^{s}(\mathbb{R}^{N})$
.◻
Appendix A. Hölder regularity for the heat equation
In this section, we state a classical regularity result for the heat equation (1.1). For completeness, we give the proof, which is based on classical arguments.
Theorem A.1. Let
![]() $\unicode[STIX]{x1D6FC}>0$
, let
$\unicode[STIX]{x1D6FC}>0$
, let
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}$
, let
$\unicode[STIX]{x1D706}\in \mathbb{C}$
, let
![]() $u_{0}\in C_{0}(\mathbb{R}^{N})$
, and let
$u_{0}\in C_{0}(\mathbb{R}^{N})$
, and let
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
be the corresponding maximal solution of (1.1). Fix
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
be the corresponding maximal solution of (1.1). Fix
![]() $0<\widetilde{\unicode[STIX]{x1D6FC}}<1$
with
$0<\widetilde{\unicode[STIX]{x1D6FC}}<1$
with
![]() $\widetilde{\unicode[STIX]{x1D6FC}}\leqslant \unicode[STIX]{x1D6FC}$
,
$\widetilde{\unicode[STIX]{x1D6FC}}\leqslant \unicode[STIX]{x1D6FC}$
,
![]() $0<T<T_{\max }$
, and assume further that
$0<T<T_{\max }$
, and assume further that
![]() $\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
,
$\unicode[STIX]{x1D6E5}u_{0}\in C_{0}(\mathbb{R}^{N})$
,
![]() $u_{0}\in C^{3}(\mathbb{R}^{N})$
and
$u_{0}\in C^{3}(\mathbb{R}^{N})$
and
with the notation (1.7). It follows that
![]() $\unicode[STIX]{x1D6E5}u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
, that
$\unicode[STIX]{x1D6E5}u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
, that
![]() $\unicode[STIX]{x2202}_{t}u$
,
$\unicode[STIX]{x2202}_{t}u$
,
![]() $\unicode[STIX]{x1D6FB}\unicode[STIX]{x2202}_{t}u$
, and all space derivatives of
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x2202}_{t}u$
, and all space derivatives of
![]() $u$
of order
$u$
of order
![]() ${\leqslant}3$
belong to
${\leqslant}3$
belong to
![]() $C([0,T]\times \mathbb{R}^{N})$
, and that
$C([0,T]\times \mathbb{R}^{N})$
, and that
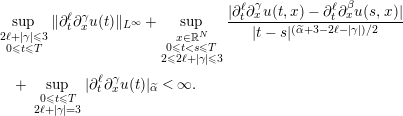 $$\begin{eqnarray}\displaystyle & & \displaystyle \sup _{\substack{ 2\ell +|\unicode[STIX]{x1D6FE}|\leqslant 3 \\ 0\leqslant t\leqslant T}}\Vert \unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}u(t)\Vert _{L^{\infty }}+\sup _{\substack{ x\in \mathbb{R}^{N} \\ 0\leqslant t<s\leqslant T \\ 2\leqslant 2\ell +|\unicode[STIX]{x1D6FE}|\leqslant 3}}\frac{|\unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}u(t,x)-\unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FD}}u(s,x)|}{|t-s|^{(\widetilde{\unicode[STIX]{x1D6FC}}+3-2\ell -|\unicode[STIX]{x1D6FE}|)/2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\sup _{\substack{ 0\leqslant t\leqslant T \\ 2\ell +|\unicode[STIX]{x1D6FE}|=3}}|\unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}u(t)|_{\widetilde{\unicode[STIX]{x1D6FC}}}<\infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \sup _{\substack{ 2\ell +|\unicode[STIX]{x1D6FE}|\leqslant 3 \\ 0\leqslant t\leqslant T}}\Vert \unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}u(t)\Vert _{L^{\infty }}+\sup _{\substack{ x\in \mathbb{R}^{N} \\ 0\leqslant t<s\leqslant T \\ 2\leqslant 2\ell +|\unicode[STIX]{x1D6FE}|\leqslant 3}}\frac{|\unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}u(t,x)-\unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FD}}u(s,x)|}{|t-s|^{(\widetilde{\unicode[STIX]{x1D6FC}}+3-2\ell -|\unicode[STIX]{x1D6FE}|)/2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\sup _{\substack{ 0\leqslant t\leqslant T \\ 2\ell +|\unicode[STIX]{x1D6FE}|=3}}|\unicode[STIX]{x2202}_{t}^{\ell }\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}u(t)|_{\widetilde{\unicode[STIX]{x1D6FC}}}<\infty .\end{eqnarray}$$
In particular,
In the above estimates,
![]() $\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x2202}_{x_{1}}^{\unicode[STIX]{x1D6FE}_{1}}\cdots \unicode[STIX]{x2202}_{x_{N}}^{\unicode[STIX]{x1D6FE}_{N}}$
if
$\unicode[STIX]{x2202}_{x}^{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x2202}_{x_{1}}^{\unicode[STIX]{x1D6FE}_{1}}\cdots \unicode[STIX]{x2202}_{x_{N}}^{\unicode[STIX]{x1D6FE}_{N}}$
if
![]() $\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{N})$
.
$\unicode[STIX]{x1D6FE}=(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{N})$
.
Proof. We define the Laplacian
![]() $A$
on
$A$
on
![]() $C_{0}(\mathbb{R}^{N})$
by
$C_{0}(\mathbb{R}^{N})$
by
We equip
![]() $D(A)$
with the graph norm
$D(A)$
with the graph norm
![]() $\Vert u\Vert _{D(A)}=\Vert u\Vert _{L^{\infty }}+\Vert \unicode[STIX]{x1D6E5}u\Vert _{L^{\infty }}$
. It follows that
$\Vert u\Vert _{D(A)}=\Vert u\Vert _{L^{\infty }}+\Vert \unicode[STIX]{x1D6E5}u\Vert _{L^{\infty }}$
. It follows that
![]() $A$
is
$A$
is
![]() $m$
-dissipative with dense domain and that
$m$
-dissipative with dense domain and that
![]() $D(A){\hookrightarrow}C_{0}^{1}(\mathbb{R}^{N})$
. More precisely,
$D(A){\hookrightarrow}C_{0}^{1}(\mathbb{R}^{N})$
. More precisely,
for all
![]() $u\in D(A)$
. Indeed, consider the Bessel potential
$u\in D(A)$
. Indeed, consider the Bessel potential
![]() $G_{\unicode[STIX]{x1D70E}}$
,
$G_{\unicode[STIX]{x1D70E}}$
,
![]() $\unicode[STIX]{x1D70E}>0$
(see [Reference Aronszajn and Smith3]). If
$\unicode[STIX]{x1D70E}>0$
(see [Reference Aronszajn and Smith3]). If
![]() $f\in C_{0}(\mathbb{R}^{N})$
, then
$f\in C_{0}(\mathbb{R}^{N})$
, then
![]() $u=G_{2}\star f$
satisfies
$u=G_{2}\star f$
satisfies
![]() $-\unicode[STIX]{x1D6E5}u+u=f$
,
$-\unicode[STIX]{x1D6E5}u+u=f$
,
![]() $u\in C_{0}(\mathbb{R}^{N})$
and
$u\in C_{0}(\mathbb{R}^{N})$
and
![]() $\unicode[STIX]{x1D6E5}u\in C_{0}(\mathbb{R}^{N})$
. Moreover, since
$\unicode[STIX]{x1D6E5}u\in C_{0}(\mathbb{R}^{N})$
. Moreover, since
![]() $\Vert G_{\unicode[STIX]{x1D70E}}\Vert _{L^{1}}=1$
(see [Reference Aronszajn and Smith3, formula (4.6
$\Vert G_{\unicode[STIX]{x1D70E}}\Vert _{L^{1}}=1$
(see [Reference Aronszajn and Smith3, formula (4.6
![]() $^{\prime }$
), p. 417]), we see that if
$^{\prime }$
), p. 417]), we see that if
![]() $u\in D(A)$
, then
$u\in D(A)$
, then
![]() $\Vert u\Vert _{L^{\infty }}\leqslant \Vert -\unicode[STIX]{x1D6E5}u+u\Vert _{L^{\infty }}$
. By an obvious scaling argument, we see that
$\Vert u\Vert _{L^{\infty }}\leqslant \Vert -\unicode[STIX]{x1D6E5}u+u\Vert _{L^{\infty }}$
. By an obvious scaling argument, we see that
![]() $\unicode[STIX]{x1D70C}\Vert u\Vert _{L^{\infty }}\leqslant \Vert -\unicode[STIX]{x1D6E5}u+\unicode[STIX]{x1D70C}u\Vert _{L^{\infty }}$
for all
$\unicode[STIX]{x1D70C}\Vert u\Vert _{L^{\infty }}\leqslant \Vert -\unicode[STIX]{x1D6E5}u+\unicode[STIX]{x1D70C}u\Vert _{L^{\infty }}$
for all
![]() $\unicode[STIX]{x1D70C}>0$
. Thus,
$\unicode[STIX]{x1D70C}>0$
. Thus,
![]() $A$
is
$A$
is
![]() $m$
-dissipative. Furthermore,
$m$
-dissipative. Furthermore,
![]() $C_{\text{c}}^{\infty }(\mathbb{R}^{N})\subset D(A)$
, so that
$C_{\text{c}}^{\infty }(\mathbb{R}^{N})\subset D(A)$
, so that
![]() $D(A)$
is dense. To prove (A.5), consider
$D(A)$
is dense. To prove (A.5), consider
![]() $u\in D(A)$
. We have
$u\in D(A)$
. We have
![]() $u=G_{2}\star (-\unicode[STIX]{x1D6E5}u+u)$
. Since
$u=G_{2}\star (-\unicode[STIX]{x1D6E5}u+u)$
. Since
![]() $\unicode[STIX]{x1D6FB}G_{2}\in L^{1}(\mathbb{R}^{N})$
(see [Reference Aronszajn and Smith3, formula (4.5), p. 417]), we deduce that
$\unicode[STIX]{x1D6FB}G_{2}\in L^{1}(\mathbb{R}^{N})$
(see [Reference Aronszajn and Smith3, formula (4.5), p. 417]), we deduce that
![]() $\Vert \unicode[STIX]{x1D6FB}u\Vert _{L^{\infty }}\leqslant C(\Vert \unicode[STIX]{x1D6E5}u\Vert _{L^{\infty }}+\Vert u\Vert _{L^{\infty }})$
, from which (A.5) follows by scaling.
$\Vert \unicode[STIX]{x1D6FB}u\Vert _{L^{\infty }}\leqslant C(\Vert \unicode[STIX]{x1D6E5}u\Vert _{L^{\infty }}+\Vert u\Vert _{L^{\infty }})$
, from which (A.5) follows by scaling.
Let now
![]() $u_{0}\in C_{0}(\mathbb{R}^{N})$
, and let
$u_{0}\in C_{0}(\mathbb{R}^{N})$
, and let
![]() $u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
be the corresponding maximal solution of (1.1). It follows from the above observations and from Pazy [Reference Pazy18, Theorem 1.6, p. 187] that
$u\in C([0,T_{\max }),C_{0}(\mathbb{R}^{N}))$
be the corresponding maximal solution of (1.1). It follows from the above observations and from Pazy [Reference Pazy18, Theorem 1.6, p. 187] that
![]() $u\in C^{1}([0,T],C_{0}(\mathbb{R}^{N}))\cap C([0,T],D(A))$
. In particular, using (A.5),
$u\in C^{1}([0,T],C_{0}(\mathbb{R}^{N}))\cap C([0,T],D(A))$
. In particular, using (A.5),
Setting
and using the formula
we deduce from (A.6) that
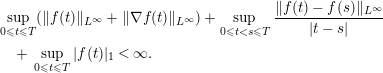 $$\begin{eqnarray}\displaystyle & & \displaystyle \sup _{0\leqslant t\leqslant T}(\Vert f(t)\Vert _{L^{\infty }}+\Vert \unicode[STIX]{x1D6FB}f(t)\Vert _{L^{\infty }})+\sup _{0\leqslant t<s\leqslant T}\frac{\Vert f(t)-f(s)\Vert _{L^{\infty }}}{|t-s|}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\sup _{0\leqslant t\leqslant T}|f(t)|_{1}<\infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \sup _{0\leqslant t\leqslant T}(\Vert f(t)\Vert _{L^{\infty }}+\Vert \unicode[STIX]{x1D6FB}f(t)\Vert _{L^{\infty }})+\sup _{0\leqslant t<s\leqslant T}\frac{\Vert f(t)-f(s)\Vert _{L^{\infty }}}{|t-s|}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\sup _{0\leqslant t\leqslant T}|f(t)|_{1}<\infty .\end{eqnarray}$$
In particular,
We apply the estimate of Ladyzhenskaya et al. [Reference Ladyzhenskaya, Solonnikov and Ural’ceva15, Chapter IV, Section 2, p. 273, estimate (2.1)] to the equations satisfied by the real and imaginary parts of
![]() $u$
, with
$u$
, with
![]() $l=\widetilde{\unicode[STIX]{x1D6FC}}$
and estimate (2.2) with
$l=\widetilde{\unicode[STIX]{x1D6FC}}$
and estimate (2.2) with
![]() $l=\widetilde{\unicode[STIX]{x1D6FC}}+2$
. It follows (among other properties) that
$l=\widetilde{\unicode[STIX]{x1D6FC}}+2$
. It follows (among other properties) that
We next recall the elementary estimate
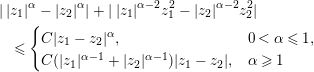 $$\begin{eqnarray}\displaystyle & & \displaystyle |\,|z_{1}|^{\unicode[STIX]{x1D6FC}}-|z_{2}|^{\unicode[STIX]{x1D6FC}}|+|\,|z_{1}|^{\unicode[STIX]{x1D6FC}-2}z_{1}^{2}-|z_{2}|^{\unicode[STIX]{x1D6FC}-2}z_{2}^{2}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left\{\begin{array}{@{}ll@{}}C|z_{1}-z_{2}|^{\unicode[STIX]{x1D6FC}},\quad & 0<\unicode[STIX]{x1D6FC}\leqslant 1,\\ C(|z_{1}|^{\unicode[STIX]{x1D6FC}-1}+|z_{2}|^{\unicode[STIX]{x1D6FC}-1})|z_{1}-z_{2}|,\quad & \unicode[STIX]{x1D6FC}\geqslant 1\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\,|z_{1}|^{\unicode[STIX]{x1D6FC}}-|z_{2}|^{\unicode[STIX]{x1D6FC}}|+|\,|z_{1}|^{\unicode[STIX]{x1D6FC}-2}z_{1}^{2}-|z_{2}|^{\unicode[STIX]{x1D6FC}-2}z_{2}^{2}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \left\{\begin{array}{@{}ll@{}}C|z_{1}-z_{2}|^{\unicode[STIX]{x1D6FC}},\quad & 0<\unicode[STIX]{x1D6FC}\leqslant 1,\\ C(|z_{1}|^{\unicode[STIX]{x1D6FC}-1}+|z_{2}|^{\unicode[STIX]{x1D6FC}-1})|z_{1}-z_{2}|,\quad & \unicode[STIX]{x1D6FC}\geqslant 1\end{array}\right.\end{eqnarray}$$
(see, e.g., [Reference Cazenave, Fang and Han7, formulas (2.26) and (2.27)]). Estimate (A.9), formula (A.8), estimates (A.12), (A.6) and (A.11) imply that
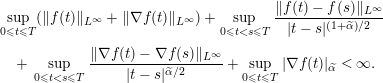 $$\begin{eqnarray}\displaystyle & & \displaystyle \sup _{0\leqslant t\leqslant T}(\Vert f(t)\Vert _{L^{\infty }}+\Vert \unicode[STIX]{x1D6FB}f(t)\Vert _{L^{\infty }})+\sup _{0\leqslant t<s\leqslant T}\frac{\Vert f(t)-f(s)\Vert _{L^{\infty }}}{|t-s|^{(1+\widetilde{\unicode[STIX]{x1D6FC}})/2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\sup _{0\leqslant t<s\leqslant T}\frac{\Vert \unicode[STIX]{x1D6FB}f(t)-\unicode[STIX]{x1D6FB}f(s)\Vert _{L^{\infty }}}{|t-s|^{\widetilde{\unicode[STIX]{x1D6FC}}/2}}+\sup _{0\leqslant t\leqslant T}|\unicode[STIX]{x1D6FB}f(t)|_{\widetilde{\unicode[STIX]{x1D6FC}}}<\infty .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \sup _{0\leqslant t\leqslant T}(\Vert f(t)\Vert _{L^{\infty }}+\Vert \unicode[STIX]{x1D6FB}f(t)\Vert _{L^{\infty }})+\sup _{0\leqslant t<s\leqslant T}\frac{\Vert f(t)-f(s)\Vert _{L^{\infty }}}{|t-s|^{(1+\widetilde{\unicode[STIX]{x1D6FC}})/2}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\sup _{0\leqslant t<s\leqslant T}\frac{\Vert \unicode[STIX]{x1D6FB}f(t)-\unicode[STIX]{x1D6FB}f(s)\Vert _{L^{\infty }}}{|t-s|^{\widetilde{\unicode[STIX]{x1D6FC}}/2}}+\sup _{0\leqslant t\leqslant T}|\unicode[STIX]{x1D6FB}f(t)|_{\widetilde{\unicode[STIX]{x1D6FC}}}<\infty .\end{eqnarray}$$
This allows us to apply again the work of Ladyzhenskaya et al. [Reference Ladyzhenskaya, Solonnikov and Ural’ceva15, Chapter IV, Section 2, p. 273], but this time we let
![]() $l=\widetilde{\unicode[STIX]{x1D6FC}}+1$
in (2.1) and
$l=\widetilde{\unicode[STIX]{x1D6FC}}+1$
in (2.1) and
![]() $l=\widetilde{\unicode[STIX]{x1D6FC}}+3$
in (2.2). The conclusion follows.◻
$l=\widetilde{\unicode[STIX]{x1D6FC}}+3$
in (2.2). The conclusion follows.◻