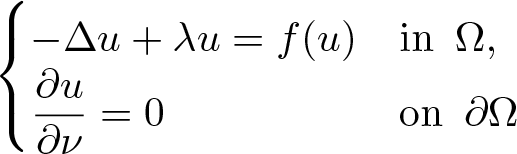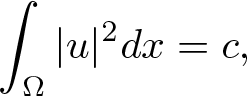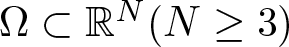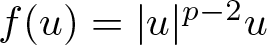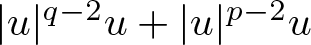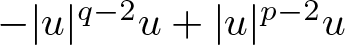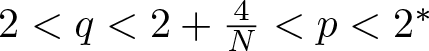1. Introduction and main results
This article is concerned with the following Neumann problem for non-linear Schrödinger (NLS) equation:
 \begin{equation}
\begin{cases}
-\Delta u+ \lambda u= f(u) & {\mathrm{in}} \,~ \Omega,\\
\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-\Delta u+ \lambda u= f(u) & {\mathrm{in}} \,~ \Omega,\\
\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega
\end{cases}
\end{equation}with a mass constraint
 \begin{equation}
\int_\Omega |u|^2 dx=c,
\end{equation}
\begin{equation}
\int_\Omega |u|^2 dx=c,
\end{equation} where ![]() $\Omega\subset \mathbb{R}^N(N\ge3)$ is a smooth bounded domain, c > 0 is a given constant, ν stands for the unit outer normal to
$\Omega\subset \mathbb{R}^N(N\ge3)$ is a smooth bounded domain, c > 0 is a given constant, ν stands for the unit outer normal to ![]() $\partial \Omega$, and λ serves as a Lagrange multiplier.
$\partial \Omega$, and λ serves as a Lagrange multiplier.
The features of problem (1.1)–(1.2) are the following:
(i) The presence of the Neumann boundary condition is quite rare in the analysis of solutions with prescribed mass.
(ii) The reaction exhibits a general mass supercritical growth at infinity.
(iii) The proof relies on powerful techniques, such as Morse theory and a new blow-up analysis for the NLS equation.
(iv) The analysis presented in this article can be extended to other classes of stationary problems, including biharmonic elliptic equations and Schrödinger–Poisson equations.
The analysis of solutions with prescribed mass is particularly significant from a physical point of view, in relationship with phenomena arising in non-linear optics, the theory of water waves, etc. Indeed, solutions with prescribed L 2-norm are especially relevant since this quantity is preserved along the time evolution. Moreover, the variational characterization of such solutions is often a strong help to analyse their orbital stability and instability properties, see [Reference Cazenave and Lions15, Reference Jeanjean, Jendrej, Le and Visciglia33, Reference Jeanjean and Le34, Reference Soave54, Reference Soave55].
The investigation of non-linear Neumann problem (1.1) finds applications in various fields. One of the main motivations stems from the analysis of standing waves in the form ![]() $\psi(t,x) = e^{-i\lambda t}u(x)$, where
$\psi(t,x) = e^{-i\lambda t}u(x)$, where ![]() $\lambda \in \mathbb{R}$ and
$\lambda \in \mathbb{R}$ and ![]() $u:\mathbb{R}^N\to \mathbb{R}$, for the time-dependent NLS equation:
$u:\mathbb{R}^N\to \mathbb{R}$, for the time-dependent NLS equation:
subject to Neumann boundary conditions. The model (1.3) plays an important role in non-linear optics and Bose–Einstein condensates (see [Reference Agrawal3, Reference Bao and Cai5, Reference Fibich and Merle23, Reference Frantzeskakis24, Reference Malomed, Condensation, Kevrekidis, Frantzeskakis and Carretero-Gonzalez40]). It is evident that ![]() $\psi(t,x)$ is a solution to (1.3) if and only
$\psi(t,x)$ is a solution to (1.3) if and only ![]() $(u, \lambda)$ constitutes a coupled solution to (1.1) with
$(u, \lambda)$ constitutes a coupled solution to (1.1) with ![]() $f(u)=g(|u|)u$. We study Eq. (1.1) by searching for solutions satisfying the mass constraint
$f(u)=g(|u|)u$. We study Eq. (1.1) by searching for solutions satisfying the mass constraint  $\int_{\Omega}|u|^2 dx=c$. In this context, λ remains unknown and emerges as a Lagrange multiplier, a feature deemed meaningful from a physical standpoint due to mass conservation. The solutions under a L 2 constraint are commonly referred to as normalized solutions. These normalized solutions to (1.1) can be obtained as critical points of the energy functional
$\int_{\Omega}|u|^2 dx=c$. In this context, λ remains unknown and emerges as a Lagrange multiplier, a feature deemed meaningful from a physical standpoint due to mass conservation. The solutions under a L 2 constraint are commonly referred to as normalized solutions. These normalized solutions to (1.1) can be obtained as critical points of the energy functional ![]() $J: H^1(\Omega)\to \mathbb{R}$ defined by:
$J: H^1(\Omega)\to \mathbb{R}$ defined by:
 \begin{equation*}J(u):=\frac{1}{2}\int_{\Omega}|\nabla u|^2 dx-\int_{\Omega} F(u) dx\end{equation*}
\begin{equation*}J(u):=\frac{1}{2}\int_{\Omega}|\nabla u|^2 dx-\int_{\Omega} F(u) dx\end{equation*}on the L 2-sphere constraint:
 \begin{equation*}\mathcal{S}_c:=\left \{u\in H^1(\Omega):~\int_{\Omega}|u|^2 dx=c \right \},\end{equation*}
\begin{equation*}\mathcal{S}_c:=\left \{u\in H^1(\Omega):~\int_{\Omega}|u|^2 dx=c \right \},\end{equation*} where  $F(u)= \int_0^u f(t)dt$.
$F(u)= \int_0^u f(t)dt$.
When ![]() $\Omega= \mathbb{R}^N$, problem (1.1)–(1.2) is transformed into
$\Omega= \mathbb{R}^N$, problem (1.1)–(1.2) is transformed into
 \begin{equation}
\begin{cases}
&-\Delta u+ \lambda u= f(u) ~~\text{in}~ \mathbb{R}^N,\\
&\displaystyle\int_{\mathbb{R}^N}|u|^2 dx=c.\\
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
&-\Delta u+ \lambda u= f(u) ~~\text{in}~ \mathbb{R}^N,\\
&\displaystyle\int_{\mathbb{R}^N}|u|^2 dx=c.\\
\end{cases}
\end{equation} Extensive studies have been conducted in recent years for this problem, particularly when considering non-linearities satisfying ![]() $f(u)\sim|u|^{p-2}u$ as
$f(u)\sim|u|^{p-2}u$ as ![]() $|u|\to+\infty$, where
$|u|\to+\infty$, where ![]() $p\in (2_*, 2^*)$ with
$p\in (2_*, 2^*)$ with  $2_*:=2+\frac{4}{N}$ and
$2_*:=2+\frac{4}{N}$ and  $2^*:=\frac{2N}{N-2}$. Within this L 2-supercritical range, the corresponding energy functional is unbounded from below on the constraint set
$2^*:=\frac{2N}{N-2}$. Within this L 2-supercritical range, the corresponding energy functional is unbounded from below on the constraint set ![]() $\mathcal{S}_c$. The pioneering work in this direction was carried out by Jeanjean [Reference Jeanjean31], where a scaled functional and mountain pass arguments were introduced to address the L 2-supercritical problems. Bartsch and Soave [Reference Bartsch and Soave6] developed a natural constraint approach to investigate the L 2-supercritical NLS equations and systems on
$\mathcal{S}_c$. The pioneering work in this direction was carried out by Jeanjean [Reference Jeanjean31], where a scaled functional and mountain pass arguments were introduced to address the L 2-supercritical problems. Bartsch and Soave [Reference Bartsch and Soave6] developed a natural constraint approach to investigate the L 2-supercritical NLS equations and systems on ![]() $\mathbb{R}^N$. For more related results on
$\mathbb{R}^N$. For more related results on ![]() $\mathbb{R}^N$, we refer to [Reference Alves, Ji and Miyagaki4, Reference Bellazzini, Forcella and Georgiev7, Reference Ikoma and Tanaka30, Reference Jeanjean, Jendrej, Le and Visciglia33, Reference Jeanjean and Le34, Reference Wei and Wu56] and the associated references.
$\mathbb{R}^N$, we refer to [Reference Alves, Ji and Miyagaki4, Reference Bellazzini, Forcella and Georgiev7, Reference Ikoma and Tanaka30, Reference Jeanjean, Jendrej, Le and Visciglia33, Reference Jeanjean and Le34, Reference Wei and Wu56] and the associated references.
The exploration of normalized solutions for the NLS on bounded domains was initialled in [Reference Noris, Tavares and Verzini46]. When ![]() $f(u)=|u|^{p-2}u$ with p being L 2-supercritical but Sobolev subcritical, Noris et al. [Reference Noris, Tavares and Verzini46] demonstrated the existence of a positive normalized solution on a unit ball with Dirichlet boundary conditions. The case for general bounded domains was addressed in [Reference Pierotti and Verzini49]. For NLS systems, one can refer to [Reference Noris, Tavares and Verzini47].
$f(u)=|u|^{p-2}u$ with p being L 2-supercritical but Sobolev subcritical, Noris et al. [Reference Noris, Tavares and Verzini46] demonstrated the existence of a positive normalized solution on a unit ball with Dirichlet boundary conditions. The case for general bounded domains was addressed in [Reference Pierotti and Verzini49]. For NLS systems, one can refer to [Reference Noris, Tavares and Verzini47].
In [Reference Pellacci, Pistoia, Vaira and Verzini48], Pellacci et al. investigated normalized solutions of the NLS under both Dirichlet and Neumann boundary conditions, focusing on the concentration of solutions at specific points of Ω as the prescribed mass c varies. Specifically, for the Neumann problem (1.1)–(1.2) with ![]() $f(u)=u^{p-1}$ for
$f(u)=u^{p-1}$ for ![]() $p\in (2_*, 2^*)$, they employed the Lyapunov–Schmidt reduction method to prove the existence of positive normalized solutions when
$p\in (2_*, 2^*)$, they employed the Lyapunov–Schmidt reduction method to prove the existence of positive normalized solutions when ![]() $c\in (0,c_0)$ for some
$c\in (0,c_0)$ for some ![]() $c_0 \gt 0$. The solutions concentrate at a point
$c_0 \gt 0$. The solutions concentrate at a point ![]() $\xi_0\in \overline\Omega$ as c → 0, where ξ 0 is either a non-degenerate critical point of the mean curvature H of the boundary
$\xi_0\in \overline\Omega$ as c → 0, where ξ 0 is either a non-degenerate critical point of the mean curvature H of the boundary ![]() $\partial\Omega$ or the maximum point of the distance function from
$\partial\Omega$ or the maximum point of the distance function from ![]() $\partial \Omega$. However, the nature of these solutions—whether they correspond to local minimizers or mountain pass-type critical points of the associated functional—remains unclear.
$\partial \Omega$. However, the nature of these solutions—whether they correspond to local minimizers or mountain pass-type critical points of the associated functional—remains unclear.
Additionally, it is noteworthy that earlier works on L 2-subcritical Schrödinger–Poisson type systems under Neumann boundary conditions can be found in [Reference Afonso and Siciliano2, Reference Pisani and Siciliano50, Reference Pisani and Siciliano51], where the authors established the existence of infinitely many normalized solutions using the Ljusternik–Schnirelmann theory.
The methodologies used for bounded domains differ significantly from those utilized in the entire space. In fact, the approaches for ![]() $\mathbb{R}^N$ heavily rely on the scaling transform
$\mathbb{R}^N$ heavily rely on the scaling transform  $(t\star u)(x)=t^{\frac{N}{2}}u(tx)$ and the associated Pohozaev identity. However, due to the lack of invariance under translations and dilation, as well as the emergence of uncontrollable boundary terms in the Pohozaev identity (particularly for non-convex domains), neither of these techniques is applicable to general bounded domains.
$(t\star u)(x)=t^{\frac{N}{2}}u(tx)$ and the associated Pohozaev identity. However, due to the lack of invariance under translations and dilation, as well as the emergence of uncontrollable boundary terms in the Pohozaev identity (particularly for non-convex domains), neither of these techniques is applicable to general bounded domains.
The normalized solutions are also explored within the framework of ergodic mean field game (MFG) systems, offering another key motivation for studying Eq. (1.1). MFGs were introduced in influential works by Huang, Caines, and Malham‘e [Reference Huang, Malhamé and Caines29] and Lasry and Lions [Reference Lasry and Lions37], independently. The primary objective of MFG is to establish a framework for characterizing Nash equilibria in differential games involving an infinite number of agents that are indistinguishable from one another. For more details, we refer interested readers to [Reference Cirant18, Reference Cirant, Cosenza and Verzini19, Reference Santambrogio53] and the references therein. From a mathematical perspective, such equilibria can be characterized by an elliptic system that combines a Kolmogorov equation and a Hamilton–Jacobi–Bellman equation. Moreover, this system has to satisfy normalization in ![]() $L^1(\Omega)$ as follows:
$L^1(\Omega)$ as follows:
 \begin{equation}
\begin{cases}
-\Delta v+ H(\nabla v)+ \lambda = h(m(x)) & {\mathrm{in}} \,~\Omega ,\\
-\Delta m- div(m \nabla H(\nabla v))=0 & {\mathrm{in}} \,~\Omega ,\\
\displaystyle\frac{\partial v}{\partial \nu}=0,~~ \frac{\partial m}{\partial \nu}+ m\nabla H(\nabla v)\cdot \nu=0 & {\mathrm{on}} \,~ \partial \Omega , \\
\displaystyle\int_\Omega m dx=1, ~~\int_\Omega v dx=0.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-\Delta v+ H(\nabla v)+ \lambda = h(m(x)) & {\mathrm{in}} \,~\Omega ,\\
-\Delta m- div(m \nabla H(\nabla v))=0 & {\mathrm{in}} \,~\Omega ,\\
\displaystyle\frac{\partial v}{\partial \nu}=0,~~ \frac{\partial m}{\partial \nu}+ m\nabla H(\nabla v)\cdot \nu=0 & {\mathrm{on}} \,~ \partial \Omega , \\
\displaystyle\int_\Omega m dx=1, ~~\int_\Omega v dx=0.
\end{cases}
\end{equation} The Neumann boundary conditions are based on the assumption that agents’ trajectories are restricted to Ω by bouncing off the boundary in a normal direction. For the quadratic Hamilton case ![]() $H(\nabla v)=|\nabla v|^2$, by using a Hopf–Cole transformation
$H(\nabla v)=|\nabla v|^2$, by using a Hopf–Cole transformation ![]() $\phi= e^{-v}/ \int e^{-v}= \sqrt{m}$, (1.5) is reduced to
$\phi= e^{-v}/ \int e^{-v}= \sqrt{m}$, (1.5) is reduced to
 \begin{equation}
\begin{cases}
-\Delta \phi =\lambda \phi- h(\phi^2)\phi & {\mathrm{in}} \,~\Omega,\\
\displaystyle\frac{\partial \phi}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\displaystyle\int_\Omega |\phi|^2 dx=1,
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-\Delta \phi =\lambda \phi- h(\phi^2)\phi & {\mathrm{in}} \,~\Omega,\\
\displaystyle\frac{\partial \phi}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\displaystyle\int_\Omega |\phi|^2 dx=1,
\end{cases}
\end{equation} which can be viewed as a single NLS equation with prescribed mass. In fact, we can check that (1.6) is equivalent to (1.1) by taking a simple transformation  $\phi= \frac{1}{\sqrt{c}}u$ and
$\phi= \frac{1}{\sqrt{c}}u$ and  $f(u)=h(\frac{u^2}{c})u$. In [Reference Cirant, Cosenza and Verzini19], Cirant et al. investigated the existence of the viscous ergodic MFG system with Neumann boundary conditions. They proved the existence of global minimizers in L 2-subcritical and critical cases, as well as local minimizers in L 2-supercritical cases.
$f(u)=h(\frac{u^2}{c})u$. In [Reference Cirant, Cosenza and Verzini19], Cirant et al. investigated the existence of the viscous ergodic MFG system with Neumann boundary conditions. They proved the existence of global minimizers in L 2-subcritical and critical cases, as well as local minimizers in L 2-supercritical cases.
When f satisfies the L 2-supercritical growth, the constraint functional ![]() $J|_{\mathcal{S}_c}$ exhibits a mountain pass geometry structure. Hence, it is natural to seek mountain pass type normalized solutions to the Neumann problem (1.1)–(1.2). However, in this scenario, the functional J becomes unbounded from below on
$J|_{\mathcal{S}_c}$ exhibits a mountain pass geometry structure. Hence, it is natural to seek mountain pass type normalized solutions to the Neumann problem (1.1)–(1.2). However, in this scenario, the functional J becomes unbounded from below on ![]() $\mathcal{S}_c$, rendering the method in [Reference Cirant, Cosenza and Verzini19] ineffective. To the best of our knowledge, there are currently no references addressing this issue. The primary aim of this article is to develop a novel variational technique to explore the existence of mountain pass type normalized solutions for (1.1)–(1.2) under the L 2-supercritical growth conditions.
$\mathcal{S}_c$, rendering the method in [Reference Cirant, Cosenza and Verzini19] ineffective. To the best of our knowledge, there are currently no references addressing this issue. The primary aim of this article is to develop a novel variational technique to explore the existence of mountain pass type normalized solutions for (1.1)–(1.2) under the L 2-supercritical growth conditions.
Furthermore, notice that the current existence results of normalized solutions for (1.4) mainly rely on the following global Ambrosetti–Rabinowitz type condition
(see [Reference Bartsch and Soave6, Reference Ikoma and Tanaka30, Reference Jeanjean31]) or combined non-linearities (see [Reference Alves, Ji and Miyagaki4, Reference Bellazzini, Forcella and Georgiev7, Reference Jeanjean, Jendrej, Le and Visciglia33, Reference Jeanjean and Le34, Reference Soave54–Reference Wei and Wu56]). Recently, normalized solutions of (1.4) have also been studied when (1.7) is replaced by certain global monotonicity conditions, as discussed in [Reference Bieganowski and Mederski10, Reference Chang, Liu and Yan17, Reference Jeanjean and Lu35, Reference Mederski and Schino42]. However, the exploration of normalized solutions on bounded domains with more diverse non-linearities beyond power non-linearity is currently limited. Our method is designed to be flexible and applies to a broad range of non-linearities, including ![]() $f(u)=|u|^{p-2}u$,
$f(u)=|u|^{p-2}u$, ![]() $|u|^{q-2}u+ |u|^{p-2}u$, and
$|u|^{q-2}u+ |u|^{p-2}u$, and ![]() $-|u|^{q-2}u+|u|^{p-2}u$, where
$-|u|^{q-2}u+|u|^{p-2}u$, where  $2 \lt q \lt 2+\frac{4}{N} \lt p \lt 2^*$, in a unified manner. Our results do not require the presence of condition (1.7) or the global monotonicity conditions. Additionally, motivated by the arguments in [Reference Pierotti and Verzini49], diverging from the prevalent focus on positive solutions in existing literature, we establish the existence of mountain pass type normalized solutions that are not necessarily positive.
$2 \lt q \lt 2+\frac{4}{N} \lt p \lt 2^*$, in a unified manner. Our results do not require the presence of condition (1.7) or the global monotonicity conditions. Additionally, motivated by the arguments in [Reference Pierotti and Verzini49], diverging from the prevalent focus on positive solutions in existing literature, we establish the existence of mountain pass type normalized solutions that are not necessarily positive.
Before stating our results, let us impose the following assumptions on f:
(f 1)
 $f\in C^1({\mathbb{R}})$,
$f\in C^1({\mathbb{R}})$,  $\lim\limits_{|t|\to 0} \frac{f(t)}{t}=0$;
$\lim\limits_{|t|\to 0} \frac{f(t)}{t}=0$;(f 2) there exist constants
 $p\in (2_*, 2^*)$ and
$p\in (2_*, 2^*)$ and  $a_0 \gt 0$ such that
$a_0 \gt 0$ such that
 \begin{equation*}\lim_{|t|\to \infty} \frac{f(t)}{|t|^{p-2}t} =a_0;\end{equation*}
\begin{equation*}\lim_{|t|\to \infty} \frac{f(t)}{|t|^{p-2}t} =a_0;\end{equation*}(f 3) there exist constants
 $\mu\geq a_0(p-1)$ and M > 0 such that
$\mu\geq a_0(p-1)$ and M > 0 such that
 \begin{equation*}\mu |t|^{p-2} \leq f'(t), ~\forall |t|\geq M. \end{equation*}
\begin{equation*}\mu |t|^{p-2} \leq f'(t), ~\forall |t|\geq M. \end{equation*}
Our main result is the following theorem.
Theorem 1.1. Suppose ![]() $(f_1)$–
$(f_1)$–![]() $(f_3)$ hold. Then there exists a constant
$(f_3)$ hold. Then there exists a constant ![]() $c^* \gt 0$ such that for any
$c^* \gt 0$ such that for any ![]() $0 \lt c \lt c^*$, problem (1.1)–(1.2) has a normalized solution pair
$0 \lt c \lt c^*$, problem (1.1)–(1.2) has a normalized solution pair ![]() $(u,\lambda)\in H^1(\Omega)\times \mathbb{R}$ of mountain pass type.
$(u,\lambda)\in H^1(\Omega)\times \mathbb{R}$ of mountain pass type.
Remark 1.2. If ![]() $f(t)t \gt 0$ for t ≠ 0, it allows us to establish the positivity of the Lagrange multiplier λ. In fact, under this condition, we can obtain a positive normalized solution u of (1.1). Subsequently, integrating Eq. (1.1) and using the Neumann boundary value condition, we can deduce that λ > 0.
$f(t)t \gt 0$ for t ≠ 0, it allows us to establish the positivity of the Lagrange multiplier λ. In fact, under this condition, we can obtain a positive normalized solution u of (1.1). Subsequently, integrating Eq. (1.1) and using the Neumann boundary value condition, we can deduce that λ > 0.
A significant challenge in proving theorem 1.1 arises from establishing the boundedness of Palais–Smale sequences. To overcome this obstacle, we combine with a parameterized minimax principle with Morse index information for constrained functionals established recently in [Reference Borthwick, Chang, Jeanjean and Soave13] (see also [Reference Borthwick, Chang, Jeanjean and Soave12, Reference Chang, Jeanjean and Soave16]) and a new blow-up analysis for the NLS equation under Neumann boundary conditions. In applying this method, the sign condition  $\int_\Omega F(u) \geq 0$ for all
$\int_\Omega F(u) \geq 0$ for all ![]() $u \in H^1(\Omega)$ is crucial to ensure the applicability of the monotonicity trick (see theorem 3.4 in §3). However, in our specific problem,
$u \in H^1(\Omega)$ is crucial to ensure the applicability of the monotonicity trick (see theorem 3.4 in §3). However, in our specific problem,  $\int_\Omega F(u)$ is not necessarily non-negative when u is not sufficiently large. Our strategy to tackle this challenge is to utilize a cut-off function and decompose f into two parts, ensuring that one of the parts satisfies this sign condition and allows for the application of the monotonicity trick.
$\int_\Omega F(u)$ is not necessarily non-negative when u is not sufficiently large. Our strategy to tackle this challenge is to utilize a cut-off function and decompose f into two parts, ensuring that one of the parts satisfies this sign condition and allows for the application of the monotonicity trick.
To address the original Neumann problem after deriving solutions for approximation problems, we will propose an innovative blow-up analysis tailored for the NLS subject to Neumann boundary conditions. In contrast to the blow-up arguments applied in the Dirichlet case (see [Reference Esposito and Petralla20, Reference Pierotti and Verzini49]), the blow-up analysis for NLS with Neumann boundary conditions, subject to the L 2-constraint, proves to be considerably more intricate. In fact, in Neumann problems, the solution is not necessarily required to vanish at the boundary ![]() $\partial\Omega$, and local extremum points of solutions can exist on the boundary. This is in stark contrast to Dirichlet problems where such extremum points are found in the interior of Ω.
$\partial\Omega$, and local extremum points of solutions can exist on the boundary. This is in stark contrast to Dirichlet problems where such extremum points are found in the interior of Ω.
We note that several studies have conducted blow-up analyses of the NLS under Neumann boundary conditions. It is well known that combining blow-up arguments with suitable Liouville-type theorems is highly effective for deriving a priori estimates. In [Reference Lin, Ni and Takagi39], Lin et al. delivered a comprehensive blow-up analysis to establish the boundedness for positive solutions to the following Neumann problem:
 \begin{equation}
\begin{cases}
-d\Delta u +u= g(u) & {\mathrm{in}} \,~\Omega,\\
\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-d\Delta u +u= g(u) & {\mathrm{in}} \,~\Omega,\\
\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\end{cases}
\end{equation}where d > 0 and g satisfies Sobolev subcritical growth conditions. The Sobolev critical case was subsequently addressed by Adimurthi et al. [Reference Adimurthi and Yadava1]. In [Reference Hu, Wang and Zhao28], Hu et al. used a blow-up argument for a non-linear Neumann problem involving the p-Laplacian to obtain a priori estimates. For further details on blow-up analyses of elliptic problems under Neumann boundary conditions, the reader is referred to [Reference Bonheure, Grumiau and Troestler11, Reference López-Gómez and Sampedro36].
Blow-up analysis can also establish a connection between the boundedness of solutions and their Morse indices. Consider the following problem:
 \begin{equation}
\begin{cases}
-\Delta u = g(x, u) & {\mathrm{in}} \,~\Omega,\\
\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-\Delta u = g(x, u) & {\mathrm{in}} \,~\Omega,\\
\displaystyle\frac{\partial u}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\end{cases}
\end{equation} where g satisfies superlinear and subcritical growth conditions. Harrabi et al. [Reference Harrabi, Ahmedou, Rebhi and Selmi27] proved that the ![]() $L^\infty$ bounds for solutions to (1.9) are equivalent to bounds on their Morse indices.
$L^\infty$ bounds for solutions to (1.9) are equivalent to bounds on their Morse indices.
In contrast to the arguments presented in [Reference Harrabi, Ahmedou, Rebhi and Selmi27], our discussion is conducted under a mass constraint and involves a family of non-linearities arising from varying Lagrange multipliers, along with a dense set used in the monotonicity trick. The most significant distinction, however, is that our blow-up analysis requires an exponential decay estimate for the solution sequence. This difference necessitates substantial modifications to the blow-up arguments in the Neumann case.
As we discussed earlier, we present a compelling argument to establish that the solution sequence not only exhibits the commonly observed exponential decay away from the boundary ![]() $\partial\Omega$, as found in the fixed frequency NLS in the Neumann case (see [Reference Ni and Takagi43, Reference Ni and Takagi44]), but more significantly, it demonstrates uniform exponential decay away from the blow-up points.
$\partial\Omega$, as found in the fixed frequency NLS in the Neumann case (see [Reference Ni and Takagi43, Reference Ni and Takagi44]), but more significantly, it demonstrates uniform exponential decay away from the blow-up points.
To conduct the blow-up analysis and subsequently derive a contradiction, a critical step involves demonstrating that the solution sequence exhibits uniform exponential decay, especially when the blow-up points are situated on the boundary ![]() $\partial\Omega$. However, in such cases, we can typically only establish that the solution sequence exponentially decays uniformly away from the blow-up points within a smaller domain in Ω, which is distant from the boundary. Specifically, as detailed in §4, through a comparison argument, we can only provide an estimation that the solution sequence exponentially decays uniformly away from the blow-up points in the domain
$\partial\Omega$. However, in such cases, we can typically only establish that the solution sequence exponentially decays uniformly away from the blow-up points within a smaller domain in Ω, which is distant from the boundary. Specifically, as detailed in §4, through a comparison argument, we can only provide an estimation that the solution sequence exponentially decays uniformly away from the blow-up points in the domain  $\tilde{\Omega}_\theta \backslash \cup_{i=1}^k (B_{R\lambda_n^{-\frac{1}{2}}}(P_n^i)\cap \tilde{\Omega}_\theta)$ (
$\tilde{\Omega}_\theta \backslash \cup_{i=1}^k (B_{R\lambda_n^{-\frac{1}{2}}}(P_n^i)\cap \tilde{\Omega}_\theta)$ (![]() $\Omega_\theta$ is defined in §4,
$\Omega_\theta$ is defined in §4, ![]() $\tilde{\Omega}_\theta:= \overline{\Omega}\backslash \Omega_\theta $ and
$\tilde{\Omega}_\theta:= \overline{\Omega}\backslash \Omega_\theta $ and ![]() $k\in\{1,2\}$). To be precise, it is demonstrated that there exist constants
$k\in\{1,2\}$). To be precise, it is demonstrated that there exist constants ![]() $C_1 \gt 0$ and
$C_1 \gt 0$ and ![]() $C_2 \gt 0$ such that
$C_2 \gt 0$ such that
 \begin{equation*}
u_n(x)\leq C_1e^{C_1 R}\lambda_n^{\frac{1}{p-2}}\sum_{i=1}^k e^{-C_2\lambda_n^{\frac{1}{2}}|x- P_n^i|},~~\forall x\in \tilde{\Omega}_\theta \backslash \cup_{i=1}^k (B_{R\lambda_n^{-\frac{1}{2}}}(P_n^i)\cap \tilde{\Omega}_\theta),
\end{equation*}
\begin{equation*}
u_n(x)\leq C_1e^{C_1 R}\lambda_n^{\frac{1}{p-2}}\sum_{i=1}^k e^{-C_2\lambda_n^{\frac{1}{2}}|x- P_n^i|},~~\forall x\in \tilde{\Omega}_\theta \backslash \cup_{i=1}^k (B_{R\lambda_n^{-\frac{1}{2}}}(P_n^i)\cap \tilde{\Omega}_\theta),
\end{equation*} where un satisfies (4.1), R > 0 is a constant, ![]() $P_n^i$ is a local extremum point,
$P_n^i$ is a local extremum point, ![]() $i\in \{1,\ldots, k\}$. However, this conclusion falls short of addressing our problem adequately. The limitation arises from the challenging nature of estimating the exponential decay of the solution in the neighbourhood near the boundary
$i\in \{1,\ldots, k\}$. However, this conclusion falls short of addressing our problem adequately. The limitation arises from the challenging nature of estimating the exponential decay of the solution in the neighbourhood near the boundary ![]() $\partial\Omega$.
$\partial\Omega$.
To overcome this limitation, we formulate a diffeomorphism, denoted as ![]() $\Phi:\Omega^\theta\to \Omega_\theta$, in a manner that expands the equation to encompass a new domain, namely,
$\Phi:\Omega^\theta\to \Omega_\theta$, in a manner that expands the equation to encompass a new domain, namely, ![]() $\overline{\Omega}\cup \Omega^\theta$, which combines the original domain Ω with an adjoining tubular neighbourhood
$\overline{\Omega}\cup \Omega^\theta$, which combines the original domain Ω with an adjoining tubular neighbourhood ![]() $\Omega^\theta$ (see §4). Employing the comparison theorem, we deduce that the solution exhibits exponential decay away from the boundary of the newly defined domain
$\Omega^\theta$ (see §4). Employing the comparison theorem, we deduce that the solution exhibits exponential decay away from the boundary of the newly defined domain ![]() $\overline{\Omega}\cup \Omega^\theta$. Subsequently, through a similar argument as mentioned earlier, we observe that the solution exponentially decays uniformly away from the blow-up points in
$\overline{\Omega}\cup \Omega^\theta$. Subsequently, through a similar argument as mentioned earlier, we observe that the solution exponentially decays uniformly away from the blow-up points in  $\overline{\Omega}\backslash \cup_{i=1}^k (B_{R\lambda_n^{-1/2}}(P_n^i)\cap \overline{\Omega})$. This establishes the intended conclusion we strive to attain.
$\overline{\Omega}\backslash \cup_{i=1}^k (B_{R\lambda_n^{-1/2}}(P_n^i)\cap \overline{\Omega})$. This establishes the intended conclusion we strive to attain.
This article is organized as follows. In §2, we provide the mountain pass geometry of the parameterized functionals Jρ uniformly for  $\rho\in[\frac{1}{2},1]$. Subsequently, in §3, we show the existence of a mountain pass critical point uρ with Morse index information for
$\rho\in[\frac{1}{2},1]$. Subsequently, in §3, we show the existence of a mountain pass critical point uρ with Morse index information for ![]() $J_\rho|_{\mathcal{S}_c}$ for almost every
$J_\rho|_{\mathcal{S}_c}$ for almost every  $\rho\in[\frac{1}{2},1]$. In §4, we perform a blow-up analysis of solutions with bounded Morse index for the Neumann problem. Finally, in §5, we prove theorem 1.1. For convenience, we denote by
$\rho\in[\frac{1}{2},1]$. In §4, we perform a blow-up analysis of solutions with bounded Morse index for the Neumann problem. Finally, in §5, we prove theorem 1.1. For convenience, we denote by ![]() $\|\cdot\|_r$ the norm of the spaces
$\|\cdot\|_r$ the norm of the spaces ![]() $L^r(\Omega)(1\le r\le +\infty)$, by
$L^r(\Omega)(1\le r\le +\infty)$, by ![]() $\|\cdot\|$ the norm in
$\|\cdot\|$ the norm in ![]() $H^1(\Omega)$.
$H^1(\Omega)$.
2. Mountain pass geometry
This section is dedicated to establishing the uniform mountain pass geometry for a parameterized functional. To achieve this goal, we first decompose f into two parts. By ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, we deduce that there exists
$(f_2)$, we deduce that there exists ![]() $R_0 \gt 0$ such that
$R_0 \gt 0$ such that ![]() $f(t)t \gt 0$ for
$f(t)t \gt 0$ for ![]() $|t|\geq R_0$. Utilizing this observation, we define
$|t|\geq R_0$. Utilizing this observation, we define
where η is a smooth cut-off function such that
 \begin{equation*}
\eta (t)=
\begin{cases}
1, &|t|\geq R_0+1,\\
0, &|t| \lt R_0
\end{cases}
\end{equation*}
\begin{equation*}
\eta (t)=
\begin{cases}
1, &|t|\geq R_0+1,\\
0, &|t| \lt R_0
\end{cases}
\end{equation*} with ![]() $|\eta'(t)|\leq 2$ for
$|\eta'(t)|\leq 2$ for ![]() $R_0 \lt |t| \lt R_0+1$. Clearly,
$R_0 \lt |t| \lt R_0+1$. Clearly, ![]() $f_1(t)t\geq 0$ for all
$f_1(t)t\geq 0$ for all ![]() $t\not =0$.
$t\not =0$.
Define ![]() $J_{\rho}: H^1(\Omega)\to \mathbb{R}$ by
$J_{\rho}: H^1(\Omega)\to \mathbb{R}$ by
 \begin{equation}
J_\rho(u):=\frac{1}{2}\int_{\Omega}|\nabla u|^2 dx- \int_\Omega F_2(u)dx-\rho\int_{\Omega}F_1(u) dx,~ u\in H^1(\Omega),~ \rho \in \left[\frac{1}{2},1\right],
\end{equation}
\begin{equation}
J_\rho(u):=\frac{1}{2}\int_{\Omega}|\nabla u|^2 dx- \int_\Omega F_2(u)dx-\rho\int_{\Omega}F_1(u) dx,~ u\in H^1(\Omega),~ \rho \in \left[\frac{1}{2},1\right],
\end{equation} where  $F_1(u)= \int_0^u f_1(t)dt$ and
$F_1(u)= \int_0^u f_1(t)dt$ and  $F_2(u)= \int_0^u f_2(t)dt$.
$F_2(u)= \int_0^u f_2(t)dt$.
We recall the Gagliardo–Nirenberg inequality (see [Reference Nirenberg45]): for every ![]() $N\geq 3$ and
$N\geq 3$ and ![]() $p\in(2,2^*)$, there exists a constant
$p\in(2,2^*)$, there exists a constant ![]() $C_{N,r,\Omega}$ depending on N, r and Ω such that
$C_{N,r,\Omega}$ depending on N, r and Ω such that
 \begin{equation*}\|u\|_r\leq C_{N,r,\Omega}\|u\|_2^{1-\gamma_r}\|u\|_{H^1(\Omega)}^{\gamma_r},~~\forall u\in H^1(\Omega),\end{equation*}
\begin{equation*}\|u\|_r\leq C_{N,r,\Omega}\|u\|_2^{1-\gamma_r}\|u\|_{H^1(\Omega)}^{\gamma_r},~~\forall u\in H^1(\Omega),\end{equation*}where
 \begin{equation*}\gamma_r:=\frac{N(r-2)}{2r}.\end{equation*}
\begin{equation*}\gamma_r:=\frac{N(r-2)}{2r}.\end{equation*} Define  $\mathcal{B}_\alpha:=\{u\in \mathcal{S}_c: \int_{\Omega} |\nabla u|^2\leq \alpha\}$,
$\mathcal{B}_\alpha:=\{u\in \mathcal{S}_c: \int_{\Omega} |\nabla u|^2\leq \alpha\}$, ![]() $\forall \alpha \gt 0$. We have the following result.
$\forall \alpha \gt 0$. We have the following result.
Lemma 2.1. Assume ![]() $(f_1)$–
$(f_1)$–![]() $(f_3)$. Then there exists
$(f_3)$. Then there exists ![]() $c^* \gt 0$ such that for any
$c^* \gt 0$ such that for any ![]() $c\in (0, c^*)$, we can find
$c\in (0, c^*)$, we can find ![]() $\alpha^* \gt 0$ such that
$\alpha^* \gt 0$ such that
 \begin{equation*}\sup_{u\in \mathcal{B}_{\alpha^*}} J_{\frac{1}{2}}(u) \lt \inf_{u\in \partial\mathcal{B}_{2\alpha^*}} J_1(u).\end{equation*}
\begin{equation*}\sup_{u\in \mathcal{B}_{\alpha^*}} J_{\frac{1}{2}}(u) \lt \inf_{u\in \partial\mathcal{B}_{2\alpha^*}} J_1(u).\end{equation*}Proof. By ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, for any ϵ, δ > 0 and
$(f_2)$, for any ϵ, δ > 0 and ![]() $q\in (2, 2_*)$, there exist constants
$q\in (2, 2_*)$, there exist constants ![]() $C^{\prime}_\epsilon, C_\delta \gt 0$ such that
$C^{\prime}_\epsilon, C_\delta \gt 0$ such that
 \begin{eqnarray}
&&F_2(u)\geq -\frac{\epsilon}{2}|u|^2 -\frac{C^{\prime}_\epsilon}{q}|u|^q,
\end{eqnarray}
\begin{eqnarray}
&&F_2(u)\geq -\frac{\epsilon}{2}|u|^2 -\frac{C^{\prime}_\epsilon}{q}|u|^q,
\end{eqnarray} \begin{eqnarray}
&&F(u)\leq \frac{\delta}{2}|u|^2 + \frac{C_\delta}{p}|u|^p.
\end{eqnarray}
\begin{eqnarray}
&&F(u)\leq \frac{\delta}{2}|u|^2 + \frac{C_\delta}{p}|u|^p.
\end{eqnarray} Let ![]() $u\in \mathcal{B}_\alpha$ and
$u\in \mathcal{B}_\alpha$ and ![]() $v\in \partial\mathcal{B}_{2\alpha}$, where α is to be determined. By (2.2)–(2.3), along with the Gagliardo–Nirenberg inequality, we obtain
$v\in \partial\mathcal{B}_{2\alpha}$, where α is to be determined. By (2.2)–(2.3), along with the Gagliardo–Nirenberg inequality, we obtain
 \begin{equation*}
\begin{aligned}
& J_1(v)-J_{\frac{1}{2}}(u)\\
&\geq \frac{1}{2}\int_\Omega |\nabla v|^2-\frac{1}{2}\int_\Omega |\nabla u|^2 -\int_\Omega F(v)+ \int_\Omega F_2(u)\\
&\geq \frac{1}{2}\int_\Omega \left( |\nabla v|^2- |\nabla u|^2 \right)dx -\frac{\delta+\epsilon}{2}c-\frac{C_\delta C_{N,p}^p}{p}c^{\frac{p(1-\gamma_p)}{2}}\|v\|^{p\gamma_p}- \frac{C^{\prime}_\epsilon C_{N,q}^q}{q}\\ &\quad \times c^{\frac{q(1-\gamma_q)}{2}}\|u\|^{q\gamma_q}\\
&\geq \frac{\alpha}{2}-\frac{\delta+\epsilon}{2}c-\frac{C_\delta C_{N,p}^p}{p}c^{\frac{p(1-\gamma_p)}{2}}(2\alpha+c)^{\frac{p\gamma_p}{2}}- \frac{C^{\prime}_\epsilon C_{N,q}^q}{q}c^{\frac{q(1-\gamma_q)}{2}}(\alpha+c)^{\frac{q\gamma_q}{2}}.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
& J_1(v)-J_{\frac{1}{2}}(u)\\
&\geq \frac{1}{2}\int_\Omega |\nabla v|^2-\frac{1}{2}\int_\Omega |\nabla u|^2 -\int_\Omega F(v)+ \int_\Omega F_2(u)\\
&\geq \frac{1}{2}\int_\Omega \left( |\nabla v|^2- |\nabla u|^2 \right)dx -\frac{\delta+\epsilon}{2}c-\frac{C_\delta C_{N,p}^p}{p}c^{\frac{p(1-\gamma_p)}{2}}\|v\|^{p\gamma_p}- \frac{C^{\prime}_\epsilon C_{N,q}^q}{q}\\ &\quad \times c^{\frac{q(1-\gamma_q)}{2}}\|u\|^{q\gamma_q}\\
&\geq \frac{\alpha}{2}-\frac{\delta+\epsilon}{2}c-\frac{C_\delta C_{N,p}^p}{p}c^{\frac{p(1-\gamma_p)}{2}}(2\alpha+c)^{\frac{p\gamma_p}{2}}- \frac{C^{\prime}_\epsilon C_{N,q}^q}{q}c^{\frac{q(1-\gamma_q)}{2}}(\alpha+c)^{\frac{q\gamma_q}{2}}.
\end{aligned}
\end{equation*} Due to the arbitrariness of ϵ and δ, we conclude that for some ![]() $c^* \gt 0$ and any
$c^* \gt 0$ and any ![]() $c\in (0, c^*)$, taking
$c\in (0, c^*)$, taking ![]() $\alpha^*= 4c$, we have
$\alpha^*= 4c$, we have
 \begin{equation*}
J_1(v)-J_{\frac{1}{2}}(u)\geq c-9^{\frac{p\gamma_p}{2}}\frac{C_1 C_{N,p}^p}{p}c^{\frac{p}{2}}- 5^{\frac{q\gamma_q}{2}}\frac{C_1' C_{N,q}^q}{q}c^{\frac{q}{2}} \gt 0.
\end{equation*}
\begin{equation*}
J_1(v)-J_{\frac{1}{2}}(u)\geq c-9^{\frac{p\gamma_p}{2}}\frac{C_1 C_{N,p}^p}{p}c^{\frac{p}{2}}- 5^{\frac{q\gamma_q}{2}}\frac{C_1' C_{N,q}^q}{q}c^{\frac{q}{2}} \gt 0.
\end{equation*}Hence, the conclusion follows.
For any ![]() $c\in (0,c^*)$, we define
$c\in (0,c^*)$, we define
 \begin{equation*}m_\rho:= \inf_{u\in \mathcal{B}_{2\alpha^*}}J_\rho(u), ~\forall\rho\in \left[\frac{1}{2},1 \right].\end{equation*}
\begin{equation*}m_\rho:= \inf_{u\in \mathcal{B}_{2\alpha^*}}J_\rho(u), ~\forall\rho\in \left[\frac{1}{2},1 \right].\end{equation*}Then, following the approach outlined in [Reference Noris, Tavares and Verzini47, proposition 3.4] (see also [Reference Bellazzini and Jeanjean8, theorem 1.6]), we can derive the following result.
Lemma 2.2. Assume ![]() $(f_1)$–
$(f_1)$–![]() $(f_3)$ and
$(f_3)$ and ![]() $c\in (0, c^*)$. Then mρ is achieved by some
$c\in (0, c^*)$. Then mρ is achieved by some ![]() $u^*_{\rho}\in \mathcal{B}_{2\alpha^*}\setminus \partial\mathcal{B}_{2\alpha^*}$.
$u^*_{\rho}\in \mathcal{B}_{2\alpha^*}\setminus \partial\mathcal{B}_{2\alpha^*}$.
Proof. Fix ![]() $c\in (0, c^*)$. By lemma 2.1, for any
$c\in (0, c^*)$. By lemma 2.1, for any  $\rho \in \left[\frac{1}{2},1 \right]$, we have
$\rho \in \left[\frac{1}{2},1 \right]$, we have
 \begin{eqnarray*}
\sup_{u\in \mathcal{B}_{\alpha^*}}J_\rho(u)
\leq \sup_{u\in \mathcal{B}_{\alpha^*}}J_{\frac{1}{2}}(u) \lt \inf_{u\in \partial\mathcal{B}_{2\alpha^*}}J_1(u)\leq \inf_{u\in \partial\mathcal{B}_{2\alpha^*}}J_\rho(u).
\end{eqnarray*}
\begin{eqnarray*}
\sup_{u\in \mathcal{B}_{\alpha^*}}J_\rho(u)
\leq \sup_{u\in \mathcal{B}_{\alpha^*}}J_{\frac{1}{2}}(u) \lt \inf_{u\in \partial\mathcal{B}_{2\alpha^*}}J_1(u)\leq \inf_{u\in \partial\mathcal{B}_{2\alpha^*}}J_\rho(u).
\end{eqnarray*} Let ![]() $\{u_{\rho,n}\}\subset \mathcal{B}_{2\alpha^*}$ be a minimizing sequence for Jρ at the level mρ. Clearly,
$\{u_{\rho,n}\}\subset \mathcal{B}_{2\alpha^*}$ be a minimizing sequence for Jρ at the level mρ. Clearly, ![]() $\{u_{\rho,n}\}$ is bounded in
$\{u_{\rho,n}\}$ is bounded in ![]() $H^1(\Omega)$. Consequently, there exist a subsequence of
$H^1(\Omega)$. Consequently, there exist a subsequence of ![]() $\{u_{\rho,n}\}$, still denoted by
$\{u_{\rho,n}\}$, still denoted by ![]() $\{u_{\rho,n}\}$, and some
$\{u_{\rho,n}\}$, and some  $u^*_\rho\in H^1(\Omega)$ such that
$u^*_\rho\in H^1(\Omega)$ such that ![]() $u_{\rho,n}\rightharpoonup u^*_\rho$ in
$u_{\rho,n}\rightharpoonup u^*_\rho$ in ![]() $H^1(\Omega)$ and
$H^1(\Omega)$ and ![]() $u_{\rho,n}\to u^*_{\rho}$ strongly in
$u_{\rho,n}\to u^*_{\rho}$ strongly in ![]() $L^r(\Omega)$ for
$L^r(\Omega)$ for ![]() $r\in[1,2^*)$. This implies that
$r\in[1,2^*)$. This implies that ![]() $u^*_{\rho}\in \mathcal{B}_{2\alpha^*}$ and thus
$u^*_{\rho}\in \mathcal{B}_{2\alpha^*}$ and thus ![]() $J_\rho(u^*_{\rho})\ge m_{\rho}.$
$J_\rho(u^*_{\rho})\ge m_{\rho}.$
By ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, together with the Hölder inequality and the Lebesgue dominated convergence theorem, we have
$(f_2)$, together with the Hölder inequality and the Lebesgue dominated convergence theorem, we have
 \begin{eqnarray*}
\int_{\Omega}\left(F(u_{\rho,n})-F(u^*_{\rho})\right)dx=\int_{\Omega}F(u_{\rho,n}-u^*_{\rho})dx+o_n(1)\to 0.
\end{eqnarray*}
\begin{eqnarray*}
\int_{\Omega}\left(F(u_{\rho,n})-F(u^*_{\rho})\right)dx=\int_{\Omega}F(u_{\rho,n}-u^*_{\rho})dx+o_n(1)\to 0.
\end{eqnarray*}Therefore, we obtain
 \begin{equation*}
J_\rho(u^*_{\rho})\le \liminf\limits_{n\to+\infty}J_\rho(u_{\rho,n})=m_{\rho}.
\end{equation*}
\begin{equation*}
J_\rho(u^*_{\rho})\le \liminf\limits_{n\to+\infty}J_\rho(u_{\rho,n})=m_{\rho}.
\end{equation*} Combining this with the previous inequality, we deduce that ![]() $J_\rho(u^*_{\rho})=m_{\rho}$ and
$J_\rho(u^*_{\rho})=m_{\rho}$ and  $\|\nabla \left(u_{\rho,n}-u^*_{\rho}\right)\|_2^2\to0$. This implies that
$\|\nabla \left(u_{\rho,n}-u^*_{\rho}\right)\|_2^2\to0$. This implies that ![]() $u_{\rho,n}\to u^*_{\rho}$ in
$u_{\rho,n}\to u^*_{\rho}$ in ![]() $H^1(\Omega)$ and hence
$H^1(\Omega)$ and hence ![]() $u^*_{\rho}$ is a minimizer of Jρ. Thus, the desired conclusion follows.
$u^*_{\rho}$ is a minimizer of Jρ. Thus, the desired conclusion follows.
Now we can show the mountain pass geometry of Jρ uniformly for  $\rho\in[\frac{1}{2}, 1]$.
$\rho\in[\frac{1}{2}, 1]$.
Lemma 2.3. Assume ![]() $(f_1)$–
$(f_1)$–![]() $(f_3)$. Then, for any
$(f_3)$. Then, for any ![]() $c\in (0,c^*)$, there exist
$c\in (0,c^*)$, there exist ![]() $w_1, w_2\in \mathcal{S}_c$ such that
$w_1, w_2\in \mathcal{S}_c$ such that
 \begin{equation*}c_\rho:= \inf_{\gamma\in \Gamma}\max_{t\in[0,1]}J_\rho(\gamma(t)) \gt \max\{J_\rho(w_1), J_\rho(w_2) \} ,~~ \forall \rho\in \left[\frac{1}{2},1 \right], \end{equation*}
\begin{equation*}c_\rho:= \inf_{\gamma\in \Gamma}\max_{t\in[0,1]}J_\rho(\gamma(t)) \gt \max\{J_\rho(w_1), J_\rho(w_2) \} ,~~ \forall \rho\in \left[\frac{1}{2},1 \right], \end{equation*}where
Proof. Let ![]() $B_r(x)$ denote a ball in
$B_r(x)$ denote a ball in ![]() $\mathbb{R}^N$, centred at
$\mathbb{R}^N$, centred at ![]() $x\in \mathbb{R}^N$ with radius r > 0. Take
$x\in \mathbb{R}^N$ with radius r > 0. Take ![]() $\phi \in C^\infty_0(B_1(0))$ with ϕ > 0 in
$\phi \in C^\infty_0(B_1(0))$ with ϕ > 0 in ![]() $B_1(0)$ such that
$B_1(0)$ such that  $\int_{B_1(0)}\phi^2 =1$. For
$\int_{B_1(0)}\phi^2 =1$. For ![]() $n\in \mathbb{N}$,
$n\in \mathbb{N}$, ![]() $x_0\in \Omega$, define
$x_0\in \Omega$, define
 \begin{equation*}
\varphi_n(x):= c^\frac{1}{2} n^\frac{N}{2} \phi (n(x-x_0)),~x\in \Omega.
\end{equation*}
\begin{equation*}
\varphi_n(x):= c^\frac{1}{2} n^\frac{N}{2} \phi (n(x-x_0)),~x\in \Omega.
\end{equation*} We can verify that ![]() $\varphi_n\in\mathcal{S}_c$ and
$\varphi_n\in\mathcal{S}_c$ and  $supp(\varphi_n)\subset B_\frac{1}{n}(x_0)\subset \Omega$ for sufficiently large n.
$supp(\varphi_n)\subset B_\frac{1}{n}(x_0)\subset \Omega$ for sufficiently large n.
By ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, taking
$(f_2)$, taking ![]() $R_0 \gt 0$ larger if necessary, there exist constants
$R_0 \gt 0$ larger if necessary, there exist constants  $C_{R_0}, C^{\prime}_{R_0}, C_p \gt 0$ such that
$C_{R_0}, C^{\prime}_{R_0}, C_p \gt 0$ such that
 \begin{eqnarray*}
&&F_1(t)\ge \frac{C_p a_0}{2p}|t|^p,~~ \forall |t|\ge 2R_0,~~~F_1(t)\ge -C_{R_0},~~ \forall |t|\le 2R_0,\\
&&F_2(t)\ge -C^{\prime}_{R_0}, \forall t\in \mathbb{R}.
\end{eqnarray*}
\begin{eqnarray*}
&&F_1(t)\ge \frac{C_p a_0}{2p}|t|^p,~~ \forall |t|\ge 2R_0,~~~F_1(t)\ge -C_{R_0},~~ \forall |t|\le 2R_0,\\
&&F_2(t)\ge -C^{\prime}_{R_0}, \forall t\in \mathbb{R}.
\end{eqnarray*} Set ![]() $\Omega_{n, 2R_0} :=\{x\in \Omega: |\varphi_n|\leq 2R_0 \}$. Then, for sufficiently large n such that
$\Omega_{n, 2R_0} :=\{x\in \Omega: |\varphi_n|\leq 2R_0 \}$. Then, for sufficiently large n such that  $\max\limits_{x\in \overline\Omega}|\varphi_n| \gt 2R_0$, we have for all
$\max\limits_{x\in \overline\Omega}|\varphi_n| \gt 2R_0$, we have for all  $\rho\in [\frac{1}{2},1]$,
$\rho\in [\frac{1}{2},1]$,
 \begin{eqnarray*}
J_\rho(\varphi_n)&\leq& \frac{1}{2}\int_{\Omega}|\nabla \varphi_n(x)|^2 + (C_{R_0}+C^{\prime}_{R_0})|\Omega| -\rho\int_{\Omega\backslash \Omega_{n, 2R_0}} \frac{C_p a_0}{2p} |\varphi_n|^p \\
&=& \frac{cn^2}{2}\int_{B_1(0)}|\nabla \phi(x)|^2 +(C_{R_0}+C^{\prime}_{R_0})|\Omega|+ \frac{2^pC_P a_0}{4p}R_0^p|\Omega|\\
&&-\frac{C_Pa_0}{4p}c^\frac{p}{2} n^{\frac{pN-2N}{2}}\int_{B_1(0)}|\phi(x)|^p\to -\infty.
\end{eqnarray*}
\begin{eqnarray*}
J_\rho(\varphi_n)&\leq& \frac{1}{2}\int_{\Omega}|\nabla \varphi_n(x)|^2 + (C_{R_0}+C^{\prime}_{R_0})|\Omega| -\rho\int_{\Omega\backslash \Omega_{n, 2R_0}} \frac{C_p a_0}{2p} |\varphi_n|^p \\
&=& \frac{cn^2}{2}\int_{B_1(0)}|\nabla \phi(x)|^2 +(C_{R_0}+C^{\prime}_{R_0})|\Omega|+ \frac{2^pC_P a_0}{4p}R_0^p|\Omega|\\
&&-\frac{C_Pa_0}{4p}c^\frac{p}{2} n^{\frac{pN-2N}{2}}\int_{B_1(0)}|\phi(x)|^p\to -\infty.
\end{eqnarray*} Hence, there exists ![]() $n_0 \gt 0 $ sufficiently large such that
$n_0 \gt 0 $ sufficiently large such that
 \begin{equation*}
J_\rho(\varphi_{n_0}) \lt J_1(u^*_{\frac{1}{2}})\le J_{\rho}(u^*_{\frac{1}{2}}), ~\forall \rho\in \left[\frac{1}{2},1 \right].
\end{equation*}
\begin{equation*}
J_\rho(\varphi_{n_0}) \lt J_1(u^*_{\frac{1}{2}})\le J_{\rho}(u^*_{\frac{1}{2}}), ~\forall \rho\in \left[\frac{1}{2},1 \right].
\end{equation*} Choose  $w_1=u^*_{\frac{1}{2}}$ and
$w_1=u^*_{\frac{1}{2}}$ and ![]() $w_2=\varphi_{n_0}$. Clearly,
$w_2=\varphi_{n_0}$. Clearly,  $u^*_{\frac{1}{2}}\in \mathcal{B}_{2\alpha^*}\setminus \partial\mathcal{B}_{2\alpha^*}, \varphi_{n_0}\not\in \mathcal{B}_{2\alpha^*}$. By continuity, for any
$u^*_{\frac{1}{2}}\in \mathcal{B}_{2\alpha^*}\setminus \partial\mathcal{B}_{2\alpha^*}, \varphi_{n_0}\not\in \mathcal{B}_{2\alpha^*}$. By continuity, for any ![]() $\gamma \in \Gamma$, there exists
$\gamma \in \Gamma$, there exists ![]() $t_\gamma \in [0,1]$ such that
$t_\gamma \in [0,1]$ such that ![]() $ \gamma(t_\gamma)\in \partial \mathcal{B}_{2\alpha^*}$. Thus, by lemma 2.1, it follows that
$ \gamma(t_\gamma)\in \partial \mathcal{B}_{2\alpha^*}$. Thus, by lemma 2.1, it follows that
 \begin{align*}
\max_{t\in[0,1]}J_\rho(\gamma(t))\geq J_\rho(\gamma(t_\gamma)) &\geq \inf_{u\in \partial \mathcal{B}_{2\alpha^*}}J_\rho(u) \gt \sup_{u\in \mathcal{B}_{\alpha^*}}J_{\frac{1}{2}}(u)\\
& \geq J_\rho(u^*_{\frac{1}{2}})=\max\{J_\rho(w_1), J_\rho(w_2)\}, ~\forall \rho\in \left[\frac{1}{2},1 \right].
\end{align*}
\begin{align*}
\max_{t\in[0,1]}J_\rho(\gamma(t))\geq J_\rho(\gamma(t_\gamma)) &\geq \inf_{u\in \partial \mathcal{B}_{2\alpha^*}}J_\rho(u) \gt \sup_{u\in \mathcal{B}_{\alpha^*}}J_{\frac{1}{2}}(u)\\
& \geq J_\rho(u^*_{\frac{1}{2}})=\max\{J_\rho(w_1), J_\rho(w_2)\}, ~\forall \rho\in \left[\frac{1}{2},1 \right].
\end{align*}The proof is now complete.
3. Existence of MP solutions for a dense set
In this section, we establish the existence of a bounded Palais–Smale sequence at level cρ for almost every  $\rho\in [\frac{1}{2},1]$. Our approach involves applying a recently developed min-max principle on the L 2-sphere, as detailed in [Reference Borthwick, Chang, Jeanjean and Soave13]. This principle integrates the monotonicity trick presented in [Reference Jeanjean32] with the min-max theorem enriched by second-order insights from Fang and Ghoussoub [Reference Fang and Ghoussoub21], which is also elaborated upon in [Reference Ghoussoub25, Chapter 11].
$\rho\in [\frac{1}{2},1]$. Our approach involves applying a recently developed min-max principle on the L 2-sphere, as detailed in [Reference Borthwick, Chang, Jeanjean and Soave13]. This principle integrates the monotonicity trick presented in [Reference Jeanjean32] with the min-max theorem enriched by second-order insights from Fang and Ghoussoub [Reference Fang and Ghoussoub21], which is also elaborated upon in [Reference Ghoussoub25, Chapter 11].
For a domain ![]() $D\subset \mathbb{R}^N$ and
$D\subset \mathbb{R}^N$ and ![]() $\phi, u\in H^1(D)$, we consider
$\phi, u\in H^1(D)$, we consider
 \begin{equation*}
Q_{\lambda,\rho}(\phi;u;D):= \int_{D}|\nabla \phi |^2 dx+ \lambda\int_{D}|\phi |^2 dx -\int_{D} f^{\prime}_2(u)\phi^2 dx -\int_{D}\rho f^{\prime}_1(u)\phi^2 dx,
\end{equation*}
\begin{equation*}
Q_{\lambda,\rho}(\phi;u;D):= \int_{D}|\nabla \phi |^2 dx+ \lambda\int_{D}|\phi |^2 dx -\int_{D} f^{\prime}_2(u)\phi^2 dx -\int_{D}\rho f^{\prime}_1(u)\phi^2 dx,
\end{equation*} where  $\lambda\in \mathbb{R}, \rho\in[\frac{1}{2},1]$. The Morse index of u, denote by m(u), is the maximum dimension of a subspace
$\lambda\in \mathbb{R}, \rho\in[\frac{1}{2},1]$. The Morse index of u, denote by m(u), is the maximum dimension of a subspace ![]() $W\subset H^1(D)$ such that
$W\subset H^1(D)$ such that ![]() $Q_{\lambda, \rho}(\phi;u;D) \lt 0$ for all
$Q_{\lambda, \rho}(\phi;u;D) \lt 0$ for all ![]() $\phi \in W\backslash \{0\}$.
$\phi \in W\backslash \{0\}$.
To state the abstract minimax theorem, we recall a general setting introduced in [Reference Berestycki and Lions9]. Let ![]() $(E, \langle\cdot,\cdot\rangle)$ and
$(E, \langle\cdot,\cdot\rangle)$ and ![]() $(H,(\cdot, \cdot))$ be two infinite dimensional Hilbert spaces such that
$(H,(\cdot, \cdot))$ be two infinite dimensional Hilbert spaces such that
with continuous injections. The continuous injection ![]() $E\hookrightarrow H$ has a norm at most 1 and E is identified with its image in H. For
$E\hookrightarrow H$ has a norm at most 1 and E is identified with its image in H. For ![]() $u\in E$, we denote
$u\in E$, we denote ![]() $\|u \|^2= \langle u,u \rangle$ and
$\|u \|^2= \langle u,u \rangle$ and ![]() $|u|^2= (u,u)$. For
$|u|^2= (u,u)$. For ![]() $a\in (0, +\infty)$, we define
$a\in (0, +\infty)$, we define ![]() $S(a):= \{u\in E, |u|^2= a\}$. We denote by
$S(a):= \{u\in E, |u|^2= a\}$. We denote by ![]() $\|\cdot\|_*$ and
$\|\cdot\|_*$ and ![]() $\|\cdot\|_{**}$, respectively, the operator norm of
$\|\cdot\|_{**}$, respectively, the operator norm of ![]() $\mathcal{L}(E, R)$ and of
$\mathcal{L}(E, R)$ and of ![]() $\mathcal{L}(E, \mathcal{L}(E, \mathbb{R}))$.
$\mathcal{L}(E, \mathcal{L}(E, \mathbb{R}))$.
Definition 3.1. [Reference Borthwick, Chang, Jeanjean and Soave13]
Let ![]() $\phi: E\to \mathbb{R}$ be a C 2-functional on E and
$\phi: E\to \mathbb{R}$ be a C 2-functional on E and ![]() $\alpha\in (0,1]$. We say that
$\alpha\in (0,1]$. We say that ![]() $\phi'$ and
$\phi'$ and ![]() $\phi^{\prime\prime}$ are α-Hölder continuous on bounded sets if for any R > 0 one can find
$\phi^{\prime\prime}$ are α-Hölder continuous on bounded sets if for any R > 0 one can find ![]() $M=M(R) \gt 0$ such that for any
$M=M(R) \gt 0$ such that for any ![]() $u_1, u_2\in B(0, R)$:
$u_1, u_2\in B(0, R)$:
Definition 3.2. [Reference Borthwick, Chang, Jeanjean and Soave13]
Let ϕ be a C 2-functional on E, for any ![]() $u\in E$ define the continuous bilinear map:
$u\in E$ define the continuous bilinear map:
 \begin{equation*}D^2\phi(u):= \phi^{\prime\prime}(u)-\frac{\phi'(u)\cdot u}{|u|^2}(\cdot, \cdot). \end{equation*}
\begin{equation*}D^2\phi(u):= \phi^{\prime\prime}(u)-\frac{\phi'(u)\cdot u}{|u|^2}(\cdot, \cdot). \end{equation*}Definition 3.3. [Reference Borthwick, Chang, Jeanjean and Soave13]
For any ![]() $u\in S(a)$ and θ > 0, we define an approximate Morse index by
$u\in S(a)$ and θ > 0, we define an approximate Morse index by
 \begin{align*}
\tilde{m}_\theta(u)&:=\sup \left\{dim ~L | L~ {\rm is~ a~ subspace ~of~ } T_uS(a)~ {\rm such~ that~} D^2\phi(u)[\phi,\phi] \lt -\theta\|\phi\|^2,\right.\\ &\qquad\qquad ~\left.\forall \varphi \in L \backslash \{0\}\right\}.
\end{align*}
\begin{align*}
\tilde{m}_\theta(u)&:=\sup \left\{dim ~L | L~ {\rm is~ a~ subspace ~of~ } T_uS(a)~ {\rm such~ that~} D^2\phi(u)[\phi,\phi] \lt -\theta\|\phi\|^2,\right.\\ &\qquad\qquad ~\left.\forall \varphi \in L \backslash \{0\}\right\}.
\end{align*} If u is a critical point for the constrained functional ![]() $\phi|_{S(a)}$ and θ = 0, then
$\phi|_{S(a)}$ and θ = 0, then ![]() $\tilde{m}_\theta(u)$ is the Morse index of u as a constrained critical point.
$\tilde{m}_\theta(u)$ is the Morse index of u as a constrained critical point.
Theorem 3.4. ([Reference Borthwick, Chang, Jeanjean and Soave13], theorem 1.5)
Let ![]() $I\subset(0, +\infty)$ be an interval and consider a family of C 2 functionals
$I\subset(0, +\infty)$ be an interval and consider a family of C 2 functionals ![]() $\Phi_\rho : E \to \mathbb{R}$ of the form:
$\Phi_\rho : E \to \mathbb{R}$ of the form:
where ![]() $B(u)\geq 0$ for every
$B(u)\geq 0$ for every ![]() $u\in E$, and
$u\in E$, and
Suppose moreover that ![]() $\Phi^{\prime}_\rho$ and
$\Phi^{\prime}_\rho$ and ![]() $\Phi'^{\prime}_\rho$ are α-Hölder continuous on bounded sets for some
$\Phi'^{\prime}_\rho$ are α-Hölder continuous on bounded sets for some ![]() $\alpha \in (0,1]$. Finally, suppose that there exist
$\alpha \in (0,1]$. Finally, suppose that there exist ![]() $w_1, w_2\in S(a)$ (independent of ρ) such that, set
$w_1, w_2\in S(a)$ (independent of ρ) such that, set
we have
 \begin{equation}
c_\rho:=\inf_{\gamma\in \Gamma}\max_{t\in [0,1]}\Phi_\rho(\gamma(t)) \gt \max\{\Phi_\rho(w_1), \Phi_\rho(w_2)\},~~\forall \rho \in I.
\end{equation}
\begin{equation}
c_\rho:=\inf_{\gamma\in \Gamma}\max_{t\in [0,1]}\Phi_\rho(\gamma(t)) \gt \max\{\Phi_\rho(w_1), \Phi_\rho(w_2)\},~~\forall \rho \in I.
\end{equation} Then, for almost every ![]() $\rho\in I$, there exist sequence
$\rho\in I$, there exist sequence ![]() $\{u_n\}\subset S(a)$ and
$\{u_n\}\subset S(a)$ and ![]() $\zeta_n\to 0^+$ such that, as
$\zeta_n\to 0^+$ such that, as ![]() $n \to \infty$,
$n \to \infty$,
(i)
 $\Phi_\rho(u_n)\to c_\rho$;
$\Phi_\rho(u_n)\to c_\rho$;(ii)
 $\|\Phi^{\prime}_\rho|_{S(a)}(u_n)\|\to 0$;
$\|\Phi^{\prime}_\rho|_{S(a)}(u_n)\|\to 0$;(iii)
 $\{u_n\}$ is bounded in E;
$\{u_n\}$ is bounded in E;(iv)
 $\tilde{m}_{\zeta_n}(u)\leq 1$.
$\tilde{m}_{\zeta_n}(u)\leq 1$.
Define ![]() $h_{\rho}(t)=\rho f_1(t)+ f_2(t)$ for
$h_{\rho}(t)=\rho f_1(t)+ f_2(t)$ for ![]() $t\in \mathbb{R}$ and
$t\in \mathbb{R}$ and  $\rho\in [\frac{1}{2},1]$. In the following, we obtain the main result of this section.
$\rho\in [\frac{1}{2},1]$. In the following, we obtain the main result of this section.
Theorem 3.5. Assume ![]() $(f_1)$–
$(f_1)$–![]() $(f_3)$ and
$(f_3)$ and ![]() $c\in (0, c^*)$. Then, for almost every
$c\in (0, c^*)$. Then, for almost every  $\rho\in [\frac{1}{2}, 1]$, there exists a critical point uρ of Jρ on
$\rho\in [\frac{1}{2}, 1]$, there exists a critical point uρ of Jρ on ![]() $\mathcal{S}_c$ at level cρ, which solves the following problem
$\mathcal{S}_c$ at level cρ, which solves the following problem
 \begin{equation}
\begin{cases}
-\Delta u_\rho+ \lambda_\rho u_\rho=h_\rho(u_\rho) & {\mathrm{in}} \,~\Omega,\\
\frac{\partial u_\rho}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-\Delta u_\rho+ \lambda_\rho u_\rho=h_\rho(u_\rho) & {\mathrm{in}} \,~\Omega,\\
\frac{\partial u_\rho}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega
\end{cases}
\end{equation} for some ![]() $\lambda_\rho \in \mathbb{R}$. Moreover, the Morse index of
$\lambda_\rho \in \mathbb{R}$. Moreover, the Morse index of ![]() $\{u_{\rho}\}$ satisfies
$\{u_{\rho}\}$ satisfies ![]() $m(u_\rho)\le 2$.
$m(u_\rho)\le 2$.
Proof. We will apply theorem 3.4 to the family of functionals Jρ, where ![]() $E=H^1(\Omega)$,
$E=H^1(\Omega)$, ![]() $H=L^2(\Omega)$,
$H=L^2(\Omega)$, ![]() $S(a)=\mathcal{S}_c$ and Γ is defined by (2.4). Specifically, we set
$S(a)=\mathcal{S}_c$ and Γ is defined by (2.4). Specifically, we set
 \begin{equation*}
A(u)= \frac{1}{2}\int_{\Omega}|\nabla u|^2dx- \int_\Omega F_2(u) dx~~{\rm and }~~B(u)=\int_{\Omega} F_1(u) dx.
\end{equation*}
\begin{equation*}
A(u)= \frac{1}{2}\int_{\Omega}|\nabla u|^2dx- \int_\Omega F_2(u) dx~~{\rm and }~~B(u)=\int_{\Omega} F_1(u) dx.
\end{equation*} Thus, we have ![]() $J_\rho(u)= A(u)-\rho B(u).$ Given that
$J_\rho(u)= A(u)-\rho B(u).$ Given that ![]() $u\in \mathcal{S}_c$ and considering the boundedness of
$u\in \mathcal{S}_c$ and considering the boundedness of  $\int_\Omega F_2(u)dx$, we deduce that
$\int_\Omega F_2(u)dx$, we deduce that
Moreover, by assumptions ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, it follows that
$(f_2)$, it follows that ![]() $J^{\prime}_\rho$ and
$J^{\prime}_\rho$ and ![]() $J'^{\prime}_\rho$ are locally Hölder continuous on
$J'^{\prime}_\rho$ are locally Hölder continuous on ![]() $\mathcal{S}_c$. By lemma 2.3, we can apply theorem 3.4 to produce a bounded Palais–Smale sequence
$\mathcal{S}_c$. By lemma 2.3, we can apply theorem 3.4 to produce a bounded Palais–Smale sequence ![]() $\{u_n\}\subset H^1(\Omega)$ for the constrained functional
$\{u_n\}\subset H^1(\Omega)$ for the constrained functional ![]() $J_{\rho}|_{\mathcal{S}_c}$ at level cρ for almost every
$J_{\rho}|_{\mathcal{S}_c}$ at level cρ for almost every  $\rho\in [\frac{1}{2}, 1]$. Additionally, there exists a sequence
$\rho\in [\frac{1}{2}, 1]$. Additionally, there exists a sequence ![]() $\zeta_n \to 0^+$ such that
$\zeta_n \to 0^+$ such that ![]() $\tilde{m}_{\zeta_n}(u_n)\leq 1$.
$\tilde{m}_{\zeta_n}(u_n)\leq 1$.
Since ![]() $\|J^{\prime}_\rho |_{\mathcal{S}_c}(u_n) \|\to 0$, and by the boundedness of
$\|J^{\prime}_\rho |_{\mathcal{S}_c}(u_n) \|\to 0$, and by the boundedness of ![]() $\{u_n\}$, there exists a sequence
$\{u_n\}$, there exists a sequence ![]() $\{\lambda_n\}\subset \mathbb{R}$ such that for any
$\{\lambda_n\}\subset \mathbb{R}$ such that for any ![]() $\varphi\in H^1(\Omega)$, we have
$\varphi\in H^1(\Omega)$, we have
 \begin{equation}
\int_{\Omega} \nabla u_n \nabla \varphi dx+\lambda_n \int_{\Omega} u_n \varphi dx - \int_{\Omega} h_{\rho}(u_n) \varphi dx =o(1).
\end{equation}
\begin{equation}
\int_{\Omega} \nabla u_n \nabla \varphi dx+\lambda_n \int_{\Omega} u_n \varphi dx - \int_{\Omega} h_{\rho}(u_n) \varphi dx =o(1).
\end{equation}This implies that
 \begin{equation*}
\int_{\Omega}|\nabla u_n|^2 dx + \lambda_n c-\int_{\Omega} h_{\rho}(u_n)u_n dx\to 0.
\end{equation*}
\begin{equation*}
\int_{\Omega}|\nabla u_n|^2 dx + \lambda_n c-\int_{\Omega} h_{\rho}(u_n)u_n dx\to 0.
\end{equation*} Using ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$ again, we deduce that
$(f_2)$ again, we deduce that ![]() $\{\lambda_n\}$ is bounded. Therefore, up to a subsequence, we may assume that
$\{\lambda_n\}$ is bounded. Therefore, up to a subsequence, we may assume that ![]() $\lambda_n \to \lambda_\rho \in \mathbb{R}$ and
$\lambda_n \to \lambda_\rho \in \mathbb{R}$ and ![]() $u_n\rightharpoonup u_{\rho}$ weakly in
$u_n\rightharpoonup u_{\rho}$ weakly in ![]() $H^1(\Omega)$. By (3.4), we obtain
$H^1(\Omega)$. By (3.4), we obtain
 \begin{equation*}
\int_{\Omega} \nabla u_\rho \nabla \varphi dx+\lambda_\rho\int_{\Omega} u_\rho \varphi dx -\int_{\Omega}h_{\rho}(u_\rho) \varphi dx=0,
\end{equation*}
\begin{equation*}
\int_{\Omega} \nabla u_\rho \nabla \varphi dx+\lambda_\rho\int_{\Omega} u_\rho \varphi dx -\int_{\Omega}h_{\rho}(u_\rho) \varphi dx=0,
\end{equation*} which implies that uρ weakly solves (3.3). By the compact embedding ![]() $H^1(\Omega)\hookrightarrow L^r(\Omega)$ for
$H^1(\Omega)\hookrightarrow L^r(\Omega)$ for ![]() $r\in[1,2^*)$ and standard arguments, we obtain that
$r\in[1,2^*)$ and standard arguments, we obtain that ![]() $u_n\to u_{\rho}$ strongly in
$u_n\to u_{\rho}$ strongly in ![]() $H^1(\Omega)$.
$H^1(\Omega)$.
It remains to show that ![]() $m(u_\rho)\le 2$. Since
$m(u_\rho)\le 2$. Since ![]() $T_u\mathcal{S}_c$ has codimension 1, noting that
$T_u\mathcal{S}_c$ has codimension 1, noting that ![]() $d^2|_{\mathcal{S}_c}J_\rho$ and
$d^2|_{\mathcal{S}_c}J_\rho$ and ![]() $T_{u_n}\mathcal{S}_c$ vary with continuity, by
$T_{u_n}\mathcal{S}_c$ vary with continuity, by ![]() $\tilde{m}_{\zeta_n}(u_n)\leq 1$ it follows that
$\tilde{m}_{\zeta_n}(u_n)\leq 1$ it follows that ![]() $\tilde{m}_0(u_\rho) \leq 1$. Then, we can use similar arguments as in [Reference Borthwick, Chang, Jeanjean and Soave12, proposition 3.5] to show
$\tilde{m}_0(u_\rho) \leq 1$. Then, we can use similar arguments as in [Reference Borthwick, Chang, Jeanjean and Soave12, proposition 3.5] to show ![]() $m(u_\rho)\leq 2$. In fact, since the tangent space
$m(u_\rho)\leq 2$. In fact, since the tangent space ![]() $T_{u}\mathcal{S}_c$ has codimension 1, it suffices to show that
$T_{u}\mathcal{S}_c$ has codimension 1, it suffices to show that ![]() $u_\rho\in \mathcal{S}_c$ has Morse index at most 1 as a constrained critical point. If this were not the case, by definition 3.3, we may assume by contradiction that there exists a subspace
$u_\rho\in \mathcal{S}_c$ has Morse index at most 1 as a constrained critical point. If this were not the case, by definition 3.3, we may assume by contradiction that there exists a subspace ![]() $W_0 \subset T_u\mathcal{S}_c$ with
$W_0 \subset T_u\mathcal{S}_c$ with ![]() $dim W_0 = 2$ such that
$dim W_0 = 2$ such that
 \begin{equation}
D^2J_\rho(u_\rho)[w, w] \lt 0~\mbox{for~all}~w\in W_0\backslash \{0\}.
\end{equation}
\begin{equation}
D^2J_\rho(u_\rho)[w, w] \lt 0~\mbox{for~all}~w\in W_0\backslash \{0\}.
\end{equation}Since W 0 is finite-dimensional, there exists a constant β > 0 such that
 \begin{equation*}
D^2J_\rho(u_\rho)[w, w] \lt -\beta~\mbox{for~all}~w\in W_0\backslash \{0\}~~\mbox{with}~~\|w\|=1.
\end{equation*}
\begin{equation*}
D^2J_\rho(u_\rho)[w, w] \lt -\beta~\mbox{for~all}~w\in W_0\backslash \{0\}~~\mbox{with}~~\|w\|=1.
\end{equation*} Using the homogeneity of ![]() $D^2J_\rho(u_\rho)$, we deduce that
$D^2J_\rho(u_\rho)$, we deduce that
 \begin{equation*}
D^2J_\rho(u_\rho)[w, w] \lt -\beta \|w\|^2~\mbox{for~all}~w\in W_0\backslash \{0\}.
\end{equation*}
\begin{equation*}
D^2J_\rho(u_\rho)[w, w] \lt -\beta \|w\|^2~\mbox{for~all}~w\in W_0\backslash \{0\}.
\end{equation*} Now, since ![]() $J_\rho'$ and
$J_\rho'$ and ![]() $J_\rho^{\prime\prime}$ are α-Hölder continuous on bounded sets for some
$J_\rho^{\prime\prime}$ are α-Hölder continuous on bounded sets for some ![]() $\alpha\in (0,1]$, it follows that there exists a sufficient small
$\alpha\in (0,1]$, it follows that there exists a sufficient small ![]() $\delta_1 \gt 0$ such that, for any
$\delta_1 \gt 0$ such that, for any ![]() $v\in \mathcal{S}_c$ satisfying
$v\in \mathcal{S}_c$ satisfying ![]() $\|v-u_\rho\|\leq \delta_1$,
$\|v-u_\rho\|\leq \delta_1$,
 \begin{equation}
D^2J_\rho(v)[w, w] \lt -\frac{\beta}{2} \|w\|^2~\mbox{for~all}~w\in W_0\backslash \{0\}.
\end{equation}
\begin{equation}
D^2J_\rho(v)[w, w] \lt -\frac{\beta}{2} \|w\|^2~\mbox{for~all}~w\in W_0\backslash \{0\}.
\end{equation} Hence, using the fact that ![]() $\|u_n-u_\rho\| \leq\delta_1$ for sufficiently large
$\|u_n-u_\rho\| \leq\delta_1$ for sufficiently large ![]() $n\in \mathbb{N}$, and in view of (3.5), (3.6), and
$n\in \mathbb{N}$, and in view of (3.5), (3.6), and ![]() $\zeta_n\to 0^+$, we obtain
$\zeta_n\to 0^+$, we obtain
 \begin{equation*}
D^2J_\rho(u_n)[w, w] \lt -\frac{\beta}{2} \|w\|^2 \lt \zeta_n \|w\|^2~\mbox{for~all}~w\in W_0\backslash \{0\}
\end{equation*}
\begin{equation*}
D^2J_\rho(u_n)[w, w] \lt -\frac{\beta}{2} \|w\|^2 \lt \zeta_n \|w\|^2~\mbox{for~all}~w\in W_0\backslash \{0\}
\end{equation*} for any such large n. Since dim![]() $W_0 \gt 1$, this provides a contradiction with theorem 3.4 (iv), recalling that
$W_0 \gt 1$, this provides a contradiction with theorem 3.4 (iv), recalling that ![]() $\zeta_n\to 0$.
$\zeta_n\to 0$.
Remark 3.6. Note that for any  $\rho\in [\frac{1}{2}, 1]$, the constant function
$\rho\in [\frac{1}{2}, 1]$, the constant function  $u_c:=\left(\frac{c}{|\Omega|}\right)^{\frac{1}{2}}$ is always a solution of (3.3) on
$u_c:=\left(\frac{c}{|\Omega|}\right)^{\frac{1}{2}}$ is always a solution of (3.3) on ![]() $\mathcal{S}_c$ for
$\mathcal{S}_c$ for  $\lambda=\frac{h_{\rho}(u_c)}{u_c}$. Under the assumptions
$\lambda=\frac{h_{\rho}(u_c)}{u_c}$. Under the assumptions ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, we can compute the constraint Morse index
$(f_2)$, we can compute the constraint Morse index ![]() $\tilde{m}_0(u_c)$ corresponding to Jρ, as demonstrated in [Reference Chang, Jeanjean and Soave16, proposition 2.1] (see also [Reference Cacciapuoti, Dovetta and Serra14, proposition 4.1]). Specifically, for any
$\tilde{m}_0(u_c)$ corresponding to Jρ, as demonstrated in [Reference Chang, Jeanjean and Soave16, proposition 2.1] (see also [Reference Cacciapuoti, Dovetta and Serra14, proposition 4.1]). Specifically, for any ![]() $c\in(0,c^*)$ with some proper
$c\in(0,c^*)$ with some proper ![]() $c^* \gt 0$, we have
$c^* \gt 0$, we have ![]() $\tilde{m}_0(u_c)=0$ for all
$\tilde{m}_0(u_c)=0$ for all  $\rho\in[\frac{1}{2}, 1]$. This implies that uc is a local minimizer of Jρ for every
$\rho\in[\frac{1}{2}, 1]$. This implies that uc is a local minimizer of Jρ for every  $\rho\in [\frac{1}{2}, 1]$. Based on this observation, we may select
$\rho\in [\frac{1}{2}, 1]$. Based on this observation, we may select ![]() $w_1=u_c$ in lemma 2.3 to construct the uniform mountain pass geometry for Jρ. Furthermore, the mountain pass type solution u obtained in theorem 1.1 cannot be a constant function, as this would contradict the fact that uc is a local minimizer.
$w_1=u_c$ in lemma 2.3 to construct the uniform mountain pass geometry for Jρ. Furthermore, the mountain pass type solution u obtained in theorem 1.1 cannot be a constant function, as this would contradict the fact that uc is a local minimizer.
4. Blow-up analysis
In this section, we develop a blow-up analysis for the sequence ![]() $\{u_{\rho_n}\}$. The goal of this analysis is to prove that
$\{u_{\rho_n}\}$. The goal of this analysis is to prove that ![]() $\{u_{\rho_n}\}$ is bounded in
$\{u_{\rho_n}\}$ is bounded in ![]() $H^1(\Omega)$. Consequently, we aim to show that
$H^1(\Omega)$. Consequently, we aim to show that ![]() $\{u_{\rho_n}\}$ converges strongly in
$\{u_{\rho_n}\}$ converges strongly in ![]() $H^1(\Omega)$ to a constrained critical point of J 1 as
$H^1(\Omega)$ to a constrained critical point of J 1 as ![]() $\rho_n\to 1^-$.
$\rho_n\to 1^-$.
For simplicity, we denote ![]() $u_n:= u_{\rho_n}$,
$u_n:= u_{\rho_n}$, ![]() $\lambda_n:=\lambda_{\rho_n}$,
$\lambda_n:=\lambda_{\rho_n}$, ![]() $c_n:= c_{\rho_n}$ in the following discussion. Here, un weakly solves the following problem
$c_n:= c_{\rho_n}$ in the following discussion. Here, un weakly solves the following problem
 \begin{equation}
\begin{cases}
-\Delta u_n+ \lambda_n u_n=h_{\rho_n}(u_n) & {\mathrm{in}} \,~ \Omega,\\
\frac{\partial u_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\int_{\Omega}|u_n|^2 dx=c,
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
-\Delta u_n+ \lambda_n u_n=h_{\rho_n}(u_n) & {\mathrm{in}} \,~ \Omega,\\
\frac{\partial u_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,\\
\int_{\Omega}|u_n|^2 dx=c,
\end{cases}
\end{equation} where ![]() $\lambda_n\in \mathbb{R}$ and
$\lambda_n\in \mathbb{R}$ and ![]() $\rho_n \to 1^-$. By theorem 3.5, we have
$\rho_n \to 1^-$. By theorem 3.5, we have ![]() $m(u_n)\le2$. Using standard regularity arguments, we obtain
$m(u_n)\le2$. Using standard regularity arguments, we obtain ![]() $u_n\in C^2(\overline{\Omega})$.
$u_n\in C^2(\overline{\Omega})$.
Lemma 4.1. There exists a constant C such that ![]() $\lambda_n\geq C$ for all n.
$\lambda_n\geq C$ for all n.
Proof. We assume by contradiction that ![]() $\lambda_n\to -\infty$. Let V be a subspace of
$\lambda_n\to -\infty$. Let V be a subspace of ![]() $H^1(\Omega)$ with dimension k, where k > 2. Define
$H^1(\Omega)$ with dimension k, where k > 2. Define ![]() $\Omega_{M_0}:=\{x\in \Omega: |u_n(x)|\leq M_0\}$, where
$\Omega_{M_0}:=\{x\in \Omega: |u_n(x)|\leq M_0\}$, where ![]() $M_0=\max\{M, R_0+1\}$ and R 0 is given in §2. By assumptions
$M_0=\max\{M, R_0+1\}$ and R 0 is given in §2. By assumptions ![]() $(f_1)$ and
$(f_1)$ and ![]() $(f_3)$, there exist constants
$(f_3)$, there exist constants  $C_{M_0}, C^{\prime}_{M_0} \gt 0$ such that for any
$C_{M_0}, C^{\prime}_{M_0} \gt 0$ such that for any ![]() $\phi\in H^1(\Omega)$,
$\phi\in H^1(\Omega)$,
 \begin{equation*}
\begin{aligned}
\int_\Omega h_{\rho_n}'(u_n)\phi^2 dx &=
\int_{\Omega_{M_0}} h_{\rho_n}'(u_n)\phi^2 dx+\int_{\Omega\backslash \Omega_{M_0}}h_{\rho_n}'(u_n)\phi^2 dx\\
&\geq \int_{\Omega_{M_0}} -C_{M_0}\phi^2 dx+ \int_{\Omega\backslash \Omega_{M_0}}h_{\rho_n}'(u_n)\phi^2 dx\\
&\geq \int_{\Omega_{M_0}} -C_{M_0}\phi^2 dx+ \int_{\Omega\backslash \Omega_{M_0}}\left(\rho_n\mu |u_n|^{p-2}- C_{M_0}'\right)\phi^2 dx.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\int_\Omega h_{\rho_n}'(u_n)\phi^2 dx &=
\int_{\Omega_{M_0}} h_{\rho_n}'(u_n)\phi^2 dx+\int_{\Omega\backslash \Omega_{M_0}}h_{\rho_n}'(u_n)\phi^2 dx\\
&\geq \int_{\Omega_{M_0}} -C_{M_0}\phi^2 dx+ \int_{\Omega\backslash \Omega_{M_0}}h_{\rho_n}'(u_n)\phi^2 dx\\
&\geq \int_{\Omega_{M_0}} -C_{M_0}\phi^2 dx+ \int_{\Omega\backslash \Omega_{M_0}}\left(\rho_n\mu |u_n|^{p-2}- C_{M_0}'\right)\phi^2 dx.
\end{aligned}
\end{equation*} Taking ![]() $\varphi\in V\setminus\{0\}$, we obtain
$\varphi\in V\setminus\{0\}$, we obtain
 \begin{equation*}
\begin{aligned}
Q_{\lambda_n,\rho_n}(\varphi;u_n;\Omega)
&\leq \int_{\Omega}|\nabla \varphi |^2 dx+ \lambda_n\int_{\Omega}\phi ^2 dx +\int_{\Omega_{M_0}} C_{M_0} \varphi^2 dx\\
&-\int_{\Omega\backslash \Omega_{M_0}} \left(\mu |u_n|^{p-2}- C_{M_0}'\right)\varphi^2 dx\\
&\leq \|\varphi\|^2 + \left(\lambda_n+C_{M_0}+ C_{M_0}'-1\right)\int_{\Omega}\varphi^2 dx.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
Q_{\lambda_n,\rho_n}(\varphi;u_n;\Omega)
&\leq \int_{\Omega}|\nabla \varphi |^2 dx+ \lambda_n\int_{\Omega}\phi ^2 dx +\int_{\Omega_{M_0}} C_{M_0} \varphi^2 dx\\
&-\int_{\Omega\backslash \Omega_{M_0}} \left(\mu |u_n|^{p-2}- C_{M_0}'\right)\varphi^2 dx\\
&\leq \|\varphi\|^2 + \left(\lambda_n+C_{M_0}+ C_{M_0}'-1\right)\int_{\Omega}\varphi^2 dx.
\end{aligned}
\end{equation*} This implies that ![]() $Q_{\lambda_n,\rho_n}(\varphi;u_n;\Omega)$ is negative definite on V for sufficiently large n, which contradicts the fact that
$Q_{\lambda_n,\rho_n}(\varphi;u_n;\Omega)$ is negative definite on V for sufficiently large n, which contradicts the fact that ![]() $m(u_n)\le 2$.
$m(u_n)\le 2$.
Lemma 4.2. If ![]() $\lambda_n \to +\infty$, then
$\lambda_n \to +\infty$, then ![]() $\|u_n \|_{L^\infty} \to +\infty$.
$\|u_n \|_{L^\infty} \to +\infty$.
Proof. By (4.1) and assumptions ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, there exists a constant
$(f_2)$, there exists a constant ![]() $C_1 \gt 0$ such that
$C_1 \gt 0$ such that
 \begin{equation*}
\lambda_nc\leq \int_\Omega f(u_n)u_n \leq c+\int_\Omega C_1 |u_n|^p dx\le c+C_1|\Omega|\|u_n \|_{L^{\infty }}^p.
\end{equation*}
\begin{equation*}
\lambda_nc\leq \int_\Omega f(u_n)u_n \leq c+\int_\Omega C_1 |u_n|^p dx\le c+C_1|\Omega|\|u_n \|_{L^{\infty }}^p.
\end{equation*}This implies that
 \begin{equation*}
\|u_n \|_{L^{\infty }}\geq \left(\frac{c}{C_1|\Omega |} \right)^{\frac{1}{p}} (\lambda_n-1)^{\frac{1}{p}} \to +\infty.
\end{equation*}
\begin{equation*}
\|u_n \|_{L^{\infty }}\geq \left(\frac{c}{C_1|\Omega |} \right)^{\frac{1}{p}} (\lambda_n-1)^{\frac{1}{p}} \to +\infty.
\end{equation*} In the following, we will analyse the asymptotic behaviour of the solution to (4.1) as ![]() $\lambda_n \to +\infty$. For simplicity, we may assume without loss of generality that
$\lambda_n \to +\infty$. For simplicity, we may assume without loss of generality that  $\max\limits_{x\in\overline{\Omega}}u_n(x) \gt 0$.
$\max\limits_{x\in\overline{\Omega}}u_n(x) \gt 0$.
We begin by providing a local description of the blow-up points.
Lemma 4.3. Suppose that ![]() $\lambda_n \to +\infty$. Let
$\lambda_n \to +\infty$. Let ![]() $P_n\in \overline{\Omega}$ be such that, for some
$P_n\in \overline{\Omega}$ be such that, for some ![]() $R_n\to \infty$,
$R_n\to \infty$,
 \begin{equation*}
|u_n(P_n)|=\max_{B_{R_n\tilde{\epsilon}_n}(P_n) \cap \overline{\Omega}}|u_n(x)| ~~where~~
\tilde{\epsilon}_n=a_0^{-\frac{1}{2}}|u_n(P_n)|^{-\frac{p-2}{2}} \to 0.
\end{equation*}
\begin{equation*}
|u_n(P_n)|=\max_{B_{R_n\tilde{\epsilon}_n}(P_n) \cap \overline{\Omega}}|u_n(x)| ~~where~~
\tilde{\epsilon}_n=a_0^{-\frac{1}{2}}|u_n(P_n)|^{-\frac{p-2}{2}} \to 0.
\end{equation*} Set  $\epsilon_n=\lambda_n^{-\frac{1}{2}}$. Then
$\epsilon_n=\lambda_n^{-\frac{1}{2}}$. Then
 \begin{equation}
\left(\frac{\tilde{\epsilon}_n}{\epsilon_n} \right)^2\to \tilde{\lambda} \in (0, a_0].
\end{equation}
\begin{equation}
\left(\frac{\tilde{\epsilon}_n}{\epsilon_n} \right)^2\to \tilde{\lambda} \in (0, a_0].
\end{equation}Suppose moreover that
 \begin{equation}
\limsup_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= +\infty.
\end{equation}
\begin{equation}
\limsup_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= +\infty.
\end{equation}Then, passing to a subsequence if necessary, we have
(i)
 $P_n\to P\in \Omega$;
$P_n\to P\in \Omega$;(ii)
 $\frac{dist(P_n, \partial\Omega)}{\epsilon_n}\to +\infty ~~as ~~n\to +\infty,$ and the scaled sequence
(4.4)
$\frac{dist(P_n, \partial\Omega)}{\epsilon_n}\to +\infty ~~as ~~n\to +\infty,$ and the scaled sequence
(4.4) \begin{equation}
v_n(x):=a_0^{\frac{1}{p-2}} \epsilon_n^{\frac{2}{p-2}}u_n(\epsilon_n x +P_n) ~~{\rm for}~~ x\in \Omega_n:=\frac{\Omega-P_n}{\epsilon_n}
\end{equation}
\begin{equation}
v_n(x):=a_0^{\frac{1}{p-2}} \epsilon_n^{\frac{2}{p-2}}u_n(\epsilon_n x +P_n) ~~{\rm for}~~ x\in \Omega_n:=\frac{\Omega-P_n}{\epsilon_n}
\end{equation}converges to some
 $v\in H^1(\mathbb{R}^N)$ in
$v\in H^1(\mathbb{R}^N)$ in  $C^2_{loc}(\mathbb{R}^N)$, where v satisfies
(4.5)
$C^2_{loc}(\mathbb{R}^N)$, where v satisfies
(4.5) \begin{equation}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \mathbb{R}^N,\\
|v(0)|=\max\limits_{x\in \mathbb{R}^N} v, \\
v(x)\to 0 ~~{\rm as}~~|x|\to +\infty;
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \mathbb{R}^N,\\
|v(0)|=\max\limits_{x\in \mathbb{R}^N} v, \\
v(x)\to 0 ~~{\rm as}~~|x|\to +\infty;
\end{array}\right.
\end{equation}(iii) there exists
 $\phi_n\in C_0^{\infty}(\Omega)$, with supp
$\phi_n\in C_0^{\infty}(\Omega)$, with supp $\phi_n \subset B_{R\epsilon_n}(P_n)$ for some R > 0, such that
$\phi_n \subset B_{R\epsilon_n}(P_n)$ for some R > 0, such that  $Q_{\lambda_n,\rho_n}(\phi_n;u_n;\Omega) \lt 0$;
$Q_{\lambda_n,\rho_n}(\phi_n;u_n;\Omega) \lt 0$;(iv) for all R > 0 and
 $q\geq 1$,
$q\geq 1$,
 \begin{equation*} \lim_{n\to \infty}\lambda_n^{\frac{N-2}{2}-\frac{q}{p-2}}\int_{B_{R\epsilon_n}(P_n)}|u_n|^q dx=\lim_{n\to \infty}\int_{B_{R}(0)}|v_n|^q dy =\int_{B_{R}(0)}|v|^q dy.
\end{equation*}
\begin{equation*} \lim_{n\to \infty}\lambda_n^{\frac{N-2}{2}-\frac{q}{p-2}}\int_{B_{R\epsilon_n}(P_n)}|u_n|^q dx=\lim_{n\to \infty}\int_{B_{R}(0)}|v_n|^q dy =\int_{B_{R}(0)}|v|^q dy.
\end{equation*}
Instead of (4.3), we suppose that
 \begin{equation}
\limsup_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n} \lt +\infty.
\end{equation}
\begin{equation}
\limsup_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n} \lt +\infty.
\end{equation}Then, passing to a subsequence if necessary, the following results hold:
(i)
 $P_n\to P\in \partial\Omega$;
$P_n\to P\in \partial\Omega$;(ii)
 $\frac{dist(P_n, \partial\Omega)}{\epsilon_n}\to d_0\geq 0 ~~as ~~n\to +\infty$, and the scaled sequence
$\frac{dist(P_n, \partial\Omega)}{\epsilon_n}\to d_0\geq 0 ~~as ~~n\to +\infty$, and the scaled sequence  $\{v_n\}$ defined in (4.4) converges to some
$\{v_n\}$ defined in (4.4) converges to some  $v\in H^1(\mathbb{R}^N_+)$ in
$v\in H^1(\mathbb{R}^N_+)$ in  $C^2_{loc}(\mathbb{R}^N_+)$ as
$C^2_{loc}(\mathbb{R}^N_+)$ as  $n\to \infty$, where v satisfies
(4.7)
$n\to \infty$, where v satisfies
(4.7) \begin{equation}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \mathbb{R}^N_+,\\
\displaystyle\frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\partial \mathbb{R}^N_+,\\
|v(0)|=\max\limits_{x\in \mathbb{R}^N_+} v, \\
v(x)\to 0 ~~{\rm as}~~|x|\to +\infty;
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \mathbb{R}^N_+,\\
\displaystyle\frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\partial \mathbb{R}^N_+,\\
|v(0)|=\max\limits_{x\in \mathbb{R}^N_+} v, \\
v(x)\to 0 ~~{\rm as}~~|x|\to +\infty;
\end{array}\right.
\end{equation}(iii) there exists
 $\phi_n\in C_0^{\infty}(\Omega)$, with supp
$\phi_n\in C_0^{\infty}(\Omega)$, with supp $\phi_n \subset B_{R\epsilon_n}(P_n)\cap \overline{\Omega}$ for some R > 0, such that
$\phi_n \subset B_{R\epsilon_n}(P_n)\cap \overline{\Omega}$ for some R > 0, such that  $Q_{\lambda_n, \rho_n}(\phi_n;u_n;\Omega) \lt 0$;
$Q_{\lambda_n, \rho_n}(\phi_n;u_n;\Omega) \lt 0$;(iv) for all R > 0 and
 $q\geq 1$,
$q\geq 1$,
 \begin{align*}
\lim_{n\to \infty}\lambda_n^{\frac{N-2}{2}-\frac{q}{p-2}}\int_{B_{R\epsilon_n}(P_n)\cap \Omega}|u_n|^q dx&=\lim_{n\to \infty}\int_{B_{R}(0)\cap \Omega_n}|v_n|^q dy \\ &=\int_{B_{R}(0)\cap \mathbb{R}^N_+}|v|^q dy.
\end{align*}
\begin{align*}
\lim_{n\to \infty}\lambda_n^{\frac{N-2}{2}-\frac{q}{p-2}}\int_{B_{R\epsilon_n}(P_n)\cap \Omega}|u_n|^q dx&=\lim_{n\to \infty}\int_{B_{R}(0)\cap \Omega_n}|v_n|^q dy \\ &=\int_{B_{R}(0)\cap \mathbb{R}^N_+}|v|^q dy.
\end{align*}
Proof. Since un may change sign, Pn can be either a positive local maximum or a negative local minimum point. For simplicity, we focus on the case where Pn is a positive local maximum point; the arguments for the negative local minimum case are analogous.
By (4.1), we get
 \begin{equation*}
0\leq \frac{-\Delta u_n(P_n)}{u_n(P_n)}= \frac{f_2(u_n(P_n))+\rho_n f_1(u_n(P_n))}{u_n(P_n)}- \lambda_n.
\end{equation*}
\begin{equation*}
0\leq \frac{-\Delta u_n(P_n)}{u_n(P_n)}= \frac{f_2(u_n(P_n))+\rho_n f_1(u_n(P_n))}{u_n(P_n)}- \lambda_n.
\end{equation*} Using ![]() $(f_2)$ and lemma 4.1, we deduce that
$(f_2)$ and lemma 4.1, we deduce that
 \begin{equation*}\frac{\lambda_n}{|u_n(P_n)|^{p-2}}\to \tilde{\lambda}\in [0, a_0] ~{\rm as}~n\to \infty. \end{equation*}
\begin{equation*}\frac{\lambda_n}{|u_n(P_n)|^{p-2}}\to \tilde{\lambda}\in [0, a_0] ~{\rm as}~n\to \infty. \end{equation*} Next, we show that ![]() $\tilde{\lambda} \gt 0$.
$\tilde{\lambda} \gt 0$.
Define the rescaled function
 \begin{equation*}
\tilde{u}_n(x):=a_0^{\frac{1}{p-2}} \tilde{\epsilon}_n^{\frac{2}{p-2}}u_n(\tilde{\epsilon}_nx+ P_n)~~{\rm for}~~ x\in \tilde{\Omega}_n:=\frac{\Omega-P_n}{\tilde{\epsilon}_n}.
\end{equation*}
\begin{equation*}
\tilde{u}_n(x):=a_0^{\frac{1}{p-2}} \tilde{\epsilon}_n^{\frac{2}{p-2}}u_n(\tilde{\epsilon}_nx+ P_n)~~{\rm for}~~ x\in \tilde{\Omega}_n:=\frac{\Omega-P_n}{\tilde{\epsilon}_n}.
\end{equation*} Clearly, ![]() $\tilde{u}_n$ satisfies
$\tilde{u}_n$ satisfies
 \begin{equation}
\left\{\begin{array}{ll}
-\Delta \tilde{u}_n +\lambda_n \tilde{\epsilon}_n^2 \tilde{u}_n =a_0^{\frac{1}{p-2}}\tilde{\epsilon}_n^{\frac{2p-2}{p-2}}h_{\rho_n}(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) & {\mathrm{in}} \,~ \tilde{\Omega}_n,\\
|\tilde{u}_n(x)|\leq |\tilde{u}_n(0)|=1 & {\mathrm{in}} \,~ \tilde{\Omega}_n, \\
\displaystyle \frac{\partial \tilde{u}_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial\tilde{\Omega}_n.
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta \tilde{u}_n +\lambda_n \tilde{\epsilon}_n^2 \tilde{u}_n =a_0^{\frac{1}{p-2}}\tilde{\epsilon}_n^{\frac{2p-2}{p-2}}h_{\rho_n}(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) & {\mathrm{in}} \,~ \tilde{\Omega}_n,\\
|\tilde{u}_n(x)|\leq |\tilde{u}_n(0)|=1 & {\mathrm{in}} \,~ \tilde{\Omega}_n, \\
\displaystyle \frac{\partial \tilde{u}_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial\tilde{\Omega}_n.
\end{array}\right.
\end{equation} Let ![]() $d_n=dist(P_n, \partial \Omega)$. Then
$d_n=dist(P_n, \partial \Omega)$. Then
 \begin{equation*}
\frac{d_n}{\tilde{\epsilon}_n}:= L\in [0, +\infty]
~~{\rm and}~~\tilde{\Omega}_n\to
\begin{cases}
&\mathbb{R}^N ~~{\rm if}~~L=+\infty;\\
&\mathbb{H}~~~~{\rm if}~~L \lt +\infty,
\end{cases}
\end{equation*}
\begin{equation*}
\frac{d_n}{\tilde{\epsilon}_n}:= L\in [0, +\infty]
~~{\rm and}~~\tilde{\Omega}_n\to
\begin{cases}
&\mathbb{R}^N ~~{\rm if}~~L=+\infty;\\
&\mathbb{H}~~~~{\rm if}~~L \lt +\infty,
\end{cases}
\end{equation*} where ![]() $\mathbb{H}$ denotes a half-space such that
$\mathbb{H}$ denotes a half-space such that ![]() $0\in \overline{\mathbb{H}}$ and
$0\in \overline{\mathbb{H}}$ and ![]() $d(0, \partial \mathbb{H})=L$. By regularity arguments, up to a subsequence,
$d(0, \partial \mathbb{H})=L$. By regularity arguments, up to a subsequence, ![]() $\tilde{u}_n\to \tilde{u}$ in
$\tilde{u}_n\to \tilde{u}$ in ![]() $C^2_{loc}(\overline{D})$, where
$C^2_{loc}(\overline{D})$, where ![]() $\tilde{u}$ solves
$\tilde{u}$ solves
 \begin{equation}
\left\{\begin{array}{ll}
-\Delta \tilde{u}+ \tilde{\lambda} \tilde{u}=|\tilde{u}|^{p-2}\tilde{u} & {\mathrm{in}} \,~ D,\\
|\tilde{u}(x)|\leq |\tilde{u}(0)|=1 & {\mathrm{in}} \,~ D, \\
\displaystyle\frac{\partial \tilde{u}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D,
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta \tilde{u}+ \tilde{\lambda} \tilde{u}=|\tilde{u}|^{p-2}\tilde{u} & {\mathrm{in}} \,~ D,\\
|\tilde{u}(x)|\leq |\tilde{u}(0)|=1 & {\mathrm{in}} \,~ D, \\
\displaystyle\frac{\partial \tilde{u}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D,
\end{array}\right.
\end{equation} where D is either ![]() $\mathbb{R}^N$ or
$\mathbb{R}^N$ or ![]() $\mathbb{H}$.
$\mathbb{H}$.
We claim that ![]() $m(\tilde{u})\le 2$. To see this, suppose for contradiction that there exists k > 2 such that there are k positive functions
$m(\tilde{u})\le 2$. To see this, suppose for contradiction that there exists k > 2 such that there are k positive functions ![]() $\phi_1, \ldots, \phi_k \in H^1(D)$, orthogonal in
$\phi_1, \ldots, \phi_k \in H^1(D)$, orthogonal in ![]() $L^2(\Omega)$, satisfying
$L^2(\Omega)$, satisfying
 \begin{equation}
\int_D |\nabla \phi_i|^2 dx + \tilde{\lambda}\int_D \phi^2 dx- \int_D (p-1)|\tilde{u}|^{p-2}\phi^2 dx \lt 0
\end{equation}
\begin{equation}
\int_D |\nabla \phi_i|^2 dx + \tilde{\lambda}\int_D \phi^2 dx- \int_D (p-1)|\tilde{u}|^{p-2}\phi^2 dx \lt 0
\end{equation} for every ![]() $i\in \{1,\ldots, k\}$.
$i\in \{1,\ldots, k\}$.
Define the rescaled functions
 \begin{equation*}\phi_{i,n}(x):= \tilde{\epsilon}_n^{-\frac{N-2}{2}}\phi_i \left(\frac{x-P_n}{\tilde{\epsilon}_n}\right).\end{equation*}
\begin{equation*}\phi_{i,n}(x):= \tilde{\epsilon}_n^{-\frac{N-2}{2}}\phi_i \left(\frac{x-P_n}{\tilde{\epsilon}_n}\right).\end{equation*}Additionally, let
 \begin{equation*}\tilde{\Omega}_{n, M_0}:= \{x\in \tilde{\Omega}_n: |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|\leq M_0\}, ~~\tilde{\Omega}_{n, M_0}^c:= \tilde{\Omega}_n\backslash \tilde{\Omega}_{n, M_0},\end{equation*}
\begin{equation*}\tilde{\Omega}_{n, M_0}:= \{x\in \tilde{\Omega}_n: |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|\leq M_0\}, ~~\tilde{\Omega}_{n, M_0}^c:= \tilde{\Omega}_n\backslash \tilde{\Omega}_{n, M_0},\end{equation*}where M 0 is as given in lemma 4.1.
By direct computations, there exist constants  $\tilde{C}_{M_0}, \tilde{C}^{\prime}_{M_0} \gt 0$ such that the following estimates hold:
$\tilde{C}_{M_0}, \tilde{C}^{\prime}_{M_0} \gt 0$ such that the following estimates hold:
 \begin{align*}
\int_{\Omega} f^{\prime}_1(u_n) \phi_{i, n}^2 dx &= \int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n \phi_i^2 f_1'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}} \tilde{u}_n) dx\\
&=\int_{\tilde{\Omega}_{n, M_0+1}} [\tilde{\epsilon}^2_n\phi_i^2 f'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\\
&+ \tilde{\epsilon}^2_n \phi_i^2 f(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) ]dx \\
&+\int_{\tilde{\Omega}_{n, M_0}^c} \tilde{\epsilon}^2_n \phi_i^2 f'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) dx\\
&\geq \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} -\tilde{C}_{M_0} \tilde{\epsilon}^2_n \phi_i^2 dx\\
&+ \int_{\tilde{\Omega}_{n, M_0}^c} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx\\
&= \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} -\tilde{C}_{M_0} \tilde{\epsilon}^2_n \phi_i^2 dx\\ &\quad + \int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx\\
&-\int_{\tilde{\Omega}_{n, M_0}} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx
\end{align*}
\begin{align*}
\int_{\Omega} f^{\prime}_1(u_n) \phi_{i, n}^2 dx &= \int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n \phi_i^2 f_1'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}} \tilde{u}_n) dx\\
&=\int_{\tilde{\Omega}_{n, M_0+1}} [\tilde{\epsilon}^2_n\phi_i^2 f'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\\
&+ \tilde{\epsilon}^2_n \phi_i^2 f(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) ]dx \\
&+\int_{\tilde{\Omega}_{n, M_0}^c} \tilde{\epsilon}^2_n \phi_i^2 f'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) dx\\
&\geq \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} -\tilde{C}_{M_0} \tilde{\epsilon}^2_n \phi_i^2 dx\\
&+ \int_{\tilde{\Omega}_{n, M_0}^c} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx\\
&= \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} -\tilde{C}_{M_0} \tilde{\epsilon}^2_n \phi_i^2 dx\\ &\quad + \int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx\\
&-\int_{\tilde{\Omega}_{n, M_0}} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx
\end{align*}and
 \begin{align*}
\int_{\Omega} f^{\prime}_2(u_n) \phi_{i, n}^2 dx &= \int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n\phi_i^2 f_2'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) dx\\
&=\int_{\tilde{\Omega}_{n, M_0}\cap supp\{\phi_i\}} [\tilde{\epsilon}^2_n\phi_i^2 f'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\\ &\quad\times(1-\eta(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n))\\
&- \tilde{\epsilon}^2_n\phi_i^2 f(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta'(a_0^{-\frac{1}{p-2}} \tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)]dx \\
&\geq \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} -\tilde{C}^{\prime}_{M_0} \tilde{\epsilon}^2_n \phi_i^2 dx.
\end{align*}
\begin{align*}
\int_{\Omega} f^{\prime}_2(u_n) \phi_{i, n}^2 dx &= \int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n\phi_i^2 f_2'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n) dx\\
&=\int_{\tilde{\Omega}_{n, M_0}\cap supp\{\phi_i\}} [\tilde{\epsilon}^2_n\phi_i^2 f'(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\\ &\quad\times(1-\eta(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n))\\
&- \tilde{\epsilon}^2_n\phi_i^2 f(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)\eta'(a_0^{-\frac{1}{p-2}} \tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n)]dx \\
&\geq \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} -\tilde{C}^{\prime}_{M_0} \tilde{\epsilon}^2_n \phi_i^2 dx.
\end{align*} Note that  $a_0^{-\frac{1}{p-2}}\tilde{u}_n\leq \tilde{\epsilon}_n^{\frac{2}{p-2}} M_0$ for
$a_0^{-\frac{1}{p-2}}\tilde{u}_n\leq \tilde{\epsilon}_n^{\frac{2}{p-2}} M_0$ for  $x\in \tilde{\Omega}_{n, M_0}$, by (4.10), it follows that
$x\in \tilde{\Omega}_{n, M_0}$, by (4.10), it follows that
 \begin{equation*}
\begin{aligned}
Q_{\lambda_n,\rho_n}(\phi_{i,n}; u_n; \Omega)&= \int_{\Omega}|\nabla\phi_{i,n} |^2 dx +\lambda_n \int_{\Omega} \phi_{i,n}^2 dx -\int_{\Omega}f_2'(u_n)\phi_{i,n}^2 dx - \rho_n \\ &\quad\times\int_{\Omega}f_1'(u_n)\phi_{i,n}^2 dx\\
&\leq \int_{\tilde{\Omega}_n}|\nabla \phi_{i} |^2 dx +\lambda_n \tilde{\epsilon}_n^2\int_{\tilde{\Omega}_n} \phi_{i}^2 dx\\ &\quad + \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} (\rho_n \tilde{C}_{M_0}+ \tilde{C}^{\prime}_{M_0}) \tilde{\epsilon}^2_n \phi_i^2 dx\\
&-\rho_n\int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx+ \rho_n\\ &\quad\times\int_{\tilde{\Omega}_{n, M_0}} \phi_i^2\mu a_0^{-1}|\tilde{u}_n|^{p-2} dx \\
&\to \int_D |\nabla \phi_i|^2 dx + \tilde{\lambda}\int_D \phi^2 dx- \int_D a_0^{-1}\mu|\tilde{u}|^{p-2}\phi^2 dx\\
&\leq \int_D |\nabla \phi_i|^2 dx + \tilde{\lambda}\int_D \phi^2 dx- \int_D (p-1)|\tilde{u}|^{p-2}\phi^2 dx \lt 0.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
Q_{\lambda_n,\rho_n}(\phi_{i,n}; u_n; \Omega)&= \int_{\Omega}|\nabla\phi_{i,n} |^2 dx +\lambda_n \int_{\Omega} \phi_{i,n}^2 dx -\int_{\Omega}f_2'(u_n)\phi_{i,n}^2 dx - \rho_n \\ &\quad\times\int_{\Omega}f_1'(u_n)\phi_{i,n}^2 dx\\
&\leq \int_{\tilde{\Omega}_n}|\nabla \phi_{i} |^2 dx +\lambda_n \tilde{\epsilon}_n^2\int_{\tilde{\Omega}_n} \phi_{i}^2 dx\\ &\quad + \int_{\tilde{\Omega}_{n, M_0} \cap supp\{\phi_i\}} (\rho_n \tilde{C}_{M_0}+ \tilde{C}^{\prime}_{M_0}) \tilde{\epsilon}^2_n \phi_i^2 dx\\
&-\rho_n\int_{\tilde{\Omega}_n} \tilde{\epsilon}^2_n \phi_i^2\mu |a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_n^{-\frac{2}{p-2}}\tilde{u}_n|^{p-2} dx+ \rho_n\\ &\quad\times\int_{\tilde{\Omega}_{n, M_0}} \phi_i^2\mu a_0^{-1}|\tilde{u}_n|^{p-2} dx \\
&\to \int_D |\nabla \phi_i|^2 dx + \tilde{\lambda}\int_D \phi^2 dx- \int_D a_0^{-1}\mu|\tilde{u}|^{p-2}\phi^2 dx\\
&\leq \int_D |\nabla \phi_i|^2 dx + \tilde{\lambda}\int_D \phi^2 dx- \int_D (p-1)|\tilde{u}|^{p-2}\phi^2 dx \lt 0.
\end{aligned}
\end{equation*} This implies that ![]() $m(u_n)\geq k \gt 2$ for sufficiently large n, thereby yielding a contradiction. Thus, the claim is valid.
$m(u_n)\geq k \gt 2$ for sufficiently large n, thereby yielding a contradiction. Thus, the claim is valid.
Having established that ![]() $\tilde u$ is a finite Morse non-trivial solution of (4.9), we can apply either [Reference Farina22, theorem 2] or [Reference Yu57, proposition 2.1]. This allows us to conclude that the occurrence of
$\tilde u$ is a finite Morse non-trivial solution of (4.9), we can apply either [Reference Farina22, theorem 2] or [Reference Yu57, proposition 2.1]. This allows us to conclude that the occurrence of ![]() $\tilde{\lambda}=0$ is ruled out, regardless of whether D is a half-space or a whole space. Consequently, we can assert that
$\tilde{\lambda}=0$ is ruled out, regardless of whether D is a half-space or a whole space. Consequently, we can assert that  $\tilde{\lambda}\in (0, a_0]$.
$\tilde{\lambda}\in (0, a_0]$.
In the sequel, we consider the sequence ![]() $\{v_n\}$ defined by (4.4). Clearly, vn satisfies
$\{v_n\}$ defined by (4.4). Clearly, vn satisfies
 \begin{equation}
\left\{\begin{array}{ll}
-\Delta v_n+ v_n=a_0^{\frac{1}{p-2}}\epsilon_n^{\frac{2p-2}{p-2}}h_{\rho_n}(a_0^{-\frac{1}{p-2}}\epsilon_n^{-\frac{2}{p-2}} v_n) & {\mathrm{in}} \,~ \Omega_n,\\
|v_n(x)|\leq |v_n(0)|=(\frac{\epsilon_n}{\tilde{\epsilon}_n})^{\frac{2}{p-2}}\to \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \Omega_n, \\
\displaystyle\frac{\partial v_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega_n.
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta v_n+ v_n=a_0^{\frac{1}{p-2}}\epsilon_n^{\frac{2p-2}{p-2}}h_{\rho_n}(a_0^{-\frac{1}{p-2}}\epsilon_n^{-\frac{2}{p-2}} v_n) & {\mathrm{in}} \,~ \Omega_n,\\
|v_n(x)|\leq |v_n(0)|=(\frac{\epsilon_n}{\tilde{\epsilon}_n})^{\frac{2}{p-2}}\to \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \Omega_n, \\
\displaystyle\frac{\partial v_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega_n.
\end{array}\right.
\end{equation} Up to a subsequence, we have ![]() $v_n\to v$ in
$v_n\to v$ in ![]() $C^2_{loc}(\overline{D})$, where D is either
$C^2_{loc}(\overline{D})$, where D is either ![]() $\mathbb{R}^N$ or a half space
$\mathbb{R}^N$ or a half space ![]() $\mathbb{H}$, and v solves
$\mathbb{H}$, and v solves
 \begin{equation}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ D,\\
|v(x)|\leq |v(0)|= \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ D, \\
\displaystyle\frac{\partial v}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D.
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ D,\\
|v(x)|\leq |v(0)|= \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ D, \\
\displaystyle\frac{\partial v}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D.
\end{array}\right.
\end{equation} Arguing as above implies that ![]() $m(v)\leq 2$.
$m(v)\leq 2$.
More precisely, we distinguish the following three cases:
(1) If
 $\limsup\limits_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= +\infty$, then
$\limsup\limits_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= +\infty$, then  $D=\mathbb{R}^N$. Using
$D=\mathbb{R}^N$. Using  $m(v)\le2$, by standard regularity arguments,
$m(v)\le2$, by standard regularity arguments,  $v\in C^2(\mathbb{R}^N)$,
$v\in C^2(\mathbb{R}^N)$,  $|v(x)|\to0$ as
$|v(x)|\to0$ as  $|x|\to+\infty$. If
$|x|\to+\infty$. If  $v\ge0$, then using the strong maximum principle and [Reference Esposito and Petralla20, theorem 1.1] we know that
$v\ge0$, then using the strong maximum principle and [Reference Esposito and Petralla20, theorem 1.1] we know that  $v \gt 0, m(v)=1$, and it coincides with the unique radial ground-state solution U 0 to
$v \gt 0, m(v)=1$, and it coincides with the unique radial ground-state solution U 0 to  $-\Delta u+u=u^{p-1}$ in
$-\Delta u+u=u^{p-1}$ in  $\mathbb{R}^N$. If v is sign-changing, then
$\mathbb{R}^N$. If v is sign-changing, then  $m(v)=2$ and v admits exactly one local maximum point and one local minimum point in Ω.
$m(v)=2$ and v admits exactly one local maximum point and one local minimum point in Ω.(2) If there exists a constant a > 0 such that
 \begin{eqnarray*}
0 \lt a\leq\limsup_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n} \lt +\infty,
\end{eqnarray*}
\begin{eqnarray*}
0 \lt a\leq\limsup_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n} \lt +\infty,
\end{eqnarray*}we may assume that
 $\lim\limits_{n\to +\infty} \frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= d \gt 0$. Then, up to subsequences,
$\lim\limits_{n\to +\infty} \frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= d \gt 0$. Then, up to subsequences,  $v_n\to v $ in
$v_n\to v $ in  $C^2_{loc}(\{x_N \gt -d\})$, and v weakly solves
$C^2_{loc}(\{x_N \gt -d\})$, and v weakly solves
 \begin{equation*}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \{x_N \gt -d\},\\
|v(x)|\leq |v(0)|= \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \{x_N \gt -d\}, \\
\displaystyle \frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\{x_N=-d\}.
\end{array}\right.
\end{equation*}
\begin{equation*}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \{x_N \gt -d\},\\
|v(x)|\leq |v(0)|= \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \{x_N \gt -d\}, \\
\displaystyle \frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\{x_N=-d\}.
\end{array}\right.
\end{equation*}Let
 $\tilde{v}(x)=v(x',x_N-d)$, where
$\tilde{v}(x)=v(x',x_N-d)$, where  $x'=(x_1,x_2,\ldots,x_{N-1})$. It is straightforward to verify that
$x'=(x_1,x_2,\ldots,x_{N-1})$. It is straightforward to verify that  $\tilde{v}$ is a finite Morse index solution to the following system:
$\tilde{v}$ is a finite Morse index solution to the following system:
 \begin{equation*}
\left\{\begin{array}{ll}
-\Delta \tilde{v}+ \tilde{v}=|\tilde{v}|^{p-2}\tilde{v} & {\mathrm{in}} \,~ \{x_N \gt 0\},\\
|\tilde{v}(x)|\leq |\tilde{v}(0,\ldots,0,d)|= \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \{x_N \gt 0\}, \\
\displaystyle \frac{\partial \tilde{v}}{\partial x_N}=0 \, &{\mathrm{on}}\,~ \{x_N=0\}.
\end{array}\right.
\end{equation*}
\begin{equation*}
\left\{\begin{array}{ll}
-\Delta \tilde{v}+ \tilde{v}=|\tilde{v}|^{p-2}\tilde{v} & {\mathrm{in}} \,~ \{x_N \gt 0\},\\
|\tilde{v}(x)|\leq |\tilde{v}(0,\ldots,0,d)|= \tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \{x_N \gt 0\}, \\
\displaystyle \frac{\partial \tilde{v}}{\partial x_N}=0 \, &{\mathrm{on}}\,~ \{x_N=0\}.
\end{array}\right.
\end{equation*}Next, we extend
 $\tilde{v}$ by reflection with respect to
$\tilde{v}$ by reflection with respect to  $\{x_N= 0\}$. Specifically, for
$\{x_N= 0\}$. Specifically, for  $(x',x_N)\in \mathbb{R}^N$, we define
$(x',x_N)\in \mathbb{R}^N$, we define
 \begin{equation*}
\hat{v}(x',x_N):=
\begin{cases}
&\tilde{v}(x',x_N) ~~~~~~~~{\rm if}~x_N\geq 0,\\
&\tilde{v}(x',-x_N)~~~~~~{\rm if}~x_N \lt 0.
\end{cases}
\end{equation*}
\begin{equation*}
\hat{v}(x',x_N):=
\begin{cases}
&\tilde{v}(x',x_N) ~~~~~~~~{\rm if}~x_N\geq 0,\\
&\tilde{v}(x',-x_N)~~~~~~{\rm if}~x_N \lt 0.
\end{cases}
\end{equation*}Consequently,
 $\hat{v}$ satisfies the equation
$\hat{v}$ satisfies the equation
 \begin{equation*}
\left\{\begin{array}{ll}
-\Delta \hat{v}+ \hat{v}=|\hat{v}|^{p-2}\hat{v} & {\mathrm{in}} \,~ \mathbb{R}^N,\\
|\hat{v}(x)|\leq |\hat{v}(0,\ldots,0,-d)|= |\hat{v}(0,\ldots,0,d)|=\tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \mathbb{R}^N, \\
\displaystyle \frac{\partial \tilde{v}}{\partial x_N}=0 \, &{\mathrm{on}}\,~ \{x_N=0\}.
\end{array}\right.
\end{equation*}
\begin{equation*}
\left\{\begin{array}{ll}
-\Delta \hat{v}+ \hat{v}=|\hat{v}|^{p-2}\hat{v} & {\mathrm{in}} \,~ \mathbb{R}^N,\\
|\hat{v}(x)|\leq |\hat{v}(0,\ldots,0,-d)|= |\hat{v}(0,\ldots,0,d)|=\tilde{\lambda}^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ \mathbb{R}^N, \\
\displaystyle \frac{\partial \tilde{v}}{\partial x_N}=0 \, &{\mathrm{on}}\,~ \{x_N=0\}.
\end{array}\right.
\end{equation*}Thus,
 $\hat{v}$ is a bounded function that solves the equation
$\hat{v}$ is a bounded function that solves the equation  $-\Delta \hat{v}+ \hat{v}=|\hat{v}|^{p-2}\hat{v}$ in
$-\Delta \hat{v}+ \hat{v}=|\hat{v}|^{p-2}\hat{v}$ in  $\mathbb{R}^N$ in the weak sense. By applying Schauder interior and boundary estimates (see [Reference Gilbarg and Trudinger26]), we conclude that
$\mathbb{R}^N$ in the weak sense. By applying Schauder interior and boundary estimates (see [Reference Gilbarg and Trudinger26]), we conclude that  $\hat{v}\in C^{2,\alpha}_{loc}({\mathbb{R}^N})$ for
$\hat{v}\in C^{2,\alpha}_{loc}({\mathbb{R}^N})$ for  $\alpha\in (0,1)$, and the regularity extends up to the hyperplane
$\alpha\in (0,1)$, and the regularity extends up to the hyperplane  $\{x_N=0\}$. Since
$\{x_N=0\}$. Since  $\hat{v}$ is symmetric across
$\hat{v}$ is symmetric across  $\{x_N=0\}$, it follows that the second derivatives of
$\{x_N=0\}$, it follows that the second derivatives of  $\hat{v}$ are continuous everywhere, including at the boundary
$\hat{v}$ are continuous everywhere, including at the boundary  $\{x_N=0\}$. Consequently, by applying elliptic regularity theory and considering that
$\{x_N=0\}$. Consequently, by applying elliptic regularity theory and considering that  $\hat{v}$ is a solution with finite Morse index, we can show that
$\hat{v}$ is a solution with finite Morse index, we can show that  $\hat{v}\in C^2(\mathbb{R}^N)$ and
$\hat{v}\in C^2(\mathbb{R}^N)$ and  $|\hat{v}(x)|\to0$ as
$|\hat{v}(x)|\to0$ as  $|x|\to+\infty$. Therefore,
$|x|\to+\infty$. Therefore,  $\tilde{v}$ must be a sign-changing solution, a situation that can occur according to [Reference McLeod, Troy and Weissle41, theorem 1]. In fact, if
$\tilde{v}$ must be a sign-changing solution, a situation that can occur according to [Reference McLeod, Troy and Weissle41, theorem 1]. In fact, if  $\hat{v}$ is a positive solution, then by applying [Reference Esposito and Petralla20, theorem 1.1] once again, we deduce that
$\hat{v}$ is a positive solution, then by applying [Reference Esposito and Petralla20, theorem 1.1] once again, we deduce that  $\hat{v}$ coincides with the unique radial ground-state solution U 0 to
$\hat{v}$ coincides with the unique radial ground-state solution U 0 to  $-\Delta u+u=u^{p-1}$ in
$-\Delta u+u=u^{p-1}$ in  $\mathbb{R}^N$. It is well known that U 0 has a unique global maximum and is a radially strictly decreasing function. This would contradict the fact that
$\mathbb{R}^N$. It is well known that U 0 has a unique global maximum and is a radially strictly decreasing function. This would contradict the fact that  $\max\limits_{x\in\mathbb{R}^N} \hat{v}=|\hat{v}(0,\ldots,0,-d)|= |\hat{v}(0,\ldots,0,d)|$.
$\max\limits_{x\in\mathbb{R}^N} \hat{v}=|\hat{v}(0,\ldots,0,-d)|= |\hat{v}(0,\ldots,0,d)|$.(3) If
 $\limsup\limits_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= 0$, then, up to a subsequence,
$\limsup\limits_{n\to +\infty}\frac{dist(P_n, \partial\Omega)}{\tilde{\epsilon}_n}= 0$, then, up to a subsequence,  $\Omega_n\to \mathbb{R}^N_+(\{x_N \gt 0\})$. By similar arguments as above,
$\Omega_n\to \mathbb{R}^N_+(\{x_N \gt 0\})$. By similar arguments as above,  $v_n\to v$ in
$v_n\to v$ in  $C^2_{loc}(\mathbb{R}^N_+)$, where v is a finite Morse index of the following equation
$C^2_{loc}(\mathbb{R}^N_+)$, where v is a finite Morse index of the following equation
 \begin{equation*}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \{x_N \gt 0\},\\
\displaystyle \frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\{x_N=0\},\\
|v(y)|\leq |v(0)|= \tilde{\lambda}^{-\frac{1}{p-2}}.
\end{array}\right.
\end{equation*}
\begin{equation*}
\left\{\begin{array}{ll}
-\Delta v+ v=|v|^{p-2}v & {\mathrm{in}} \,~ \{x_N \gt 0\},\\
\displaystyle \frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\{x_N=0\},\\
|v(y)|\leq |v(0)|= \tilde{\lambda}^{-\frac{1}{p-2}}.
\end{array}\right.
\end{equation*}Extending v by reflection with respect to
 $\{x_N=0\}$ and defining
$\{x_N=0\}$ and defining
 \begin{equation*}
\hat{v}(x',x_N):=
\begin{cases}
v(x',x_N)& ~{\rm if}~~x_N\geq 0,\\
v(x',-x_N)&~{\rm if}~~x_N \lt 0.
\end{cases}
\end{equation*}
\begin{equation*}
\hat{v}(x',x_N):=
\begin{cases}
v(x',x_N)& ~{\rm if}~~x_N\geq 0,\\
v(x',-x_N)&~{\rm if}~~x_N \lt 0.
\end{cases}
\end{equation*}Then
 $\hat{v}$ satisfies
$\hat{v}$ satisfies
 \begin{equation*}
\left\{\begin{array}{ll}
-\Delta \hat{v}+ \hat{v}=|\hat{v}|^{p-2}\hat{v} & {\mathrm{in}} \,~ \mathbb{R}^N,\\
|\hat{v}(x)|\leq |\hat{v}(0)| & {\mathrm{in}} \, \mathbb{R}^N, ~\\
\displaystyle \frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\{x_N=0\}.
\end{array}\right.
\end{equation*}
\begin{equation*}
\left\{\begin{array}{ll}
-\Delta \hat{v}+ \hat{v}=|\hat{v}|^{p-2}\hat{v} & {\mathrm{in}} \,~ \mathbb{R}^N,\\
|\hat{v}(x)|\leq |\hat{v}(0)| & {\mathrm{in}} \, \mathbb{R}^N, ~\\
\displaystyle \frac{\partial v}{\partial x_N}=0 \, &{\mathrm{on}}\,~\{x_N=0\}.
\end{array}\right.
\end{equation*}Using arguments analogous to those in case (1), we deduce that if
 $\hat{v}$ is positive, then
$\hat{v}$ is positive, then  $m(\hat{v})=1$, and thus
$m(\hat{v})=1$, and thus  $\hat{v}$ coincides with U 0. Using [Reference McLeod, Troy and Weissle41, theorem 1], it is established that
$\hat{v}$ coincides with U 0. Using [Reference McLeod, Troy and Weissle41, theorem 1], it is established that  $\hat{v}$ may exhibit sign-changing behaviour, and in such instance,
$\hat{v}$ may exhibit sign-changing behaviour, and in such instance,  $m(v)=2$.
$m(v)=2$.
All in all, we get that (ii) holds. Employing similar reasoning to [Reference Esposito and Petralla20, theorem 3.1], we conclude that (iii) and (iv) are also satisfied.
We now proceed to provide a comprehensive global blow-up analysis. The following result offers a detailed global description of the asymptotic behaviour of ![]() $\{u_n\}$ as
$\{u_n\}$ as ![]() $\lambda_n\to+\infty$.
$\lambda_n\to+\infty$.
Lemma 4.4. There exists ![]() $k\in \{1,2\}$ and sequences of points
$k\in \{1,2\}$ and sequences of points ![]() $\{P_n^1\},\ldots,\{P_n^k\}$, such that
$\{P_n^1\},\ldots,\{P_n^k\}$, such that
 \begin{equation}
|u_n(P_n^i)|= \max_{B_{R_n\lambda_n^{-1/2}}(P_n^i)\cap \overline{\Omega}}|u_n|~for ~some~R_n\to \infty, ~for ~every~i,
\end{equation}
\begin{equation}
|u_n(P_n^i)|= \max_{B_{R_n\lambda_n^{-1/2}}(P_n^i)\cap \overline{\Omega}}|u_n|~for ~some~R_n\to \infty, ~for ~every~i,
\end{equation}and moreover,
 \begin{equation}
\lim_{R\to \infty}\left(\limsup_{n\to +\infty} \lambda_n^{-\frac{1}{p-2}} \max_{d_n(x)\geq R\lambda_n^{-1/2}}|u_n(x)| \right)=0,
\end{equation}
\begin{equation}
\lim_{R\to \infty}\left(\limsup_{n\to +\infty} \lambda_n^{-\frac{1}{p-2}} \max_{d_n(x)\geq R\lambda_n^{-1/2}}|u_n(x)| \right)=0,
\end{equation} where ![]() $d_n(x)=\min\{|x-P_n^i|:i=1,\ldots,k\}$ is the distance function from
$d_n(x)=\min\{|x-P_n^i|:i=1,\ldots,k\}$ is the distance function from ![]() $\{P_n^1,\ldots, P_n^k\}$ for
$\{P_n^1,\ldots, P_n^k\}$ for ![]() $x\in \overline{\Omega}$.
$x\in \overline{\Omega}$.
Proof. Take ![]() $P_n^1\in \overline{\Omega}$ such that
$P_n^1\in \overline{\Omega}$ such that  $u_n(P_n^1)=\max\limits_{\overline{\Omega}}|u_n(x)|$. If (4.15) is satisfied for
$u_n(P_n^1)=\max\limits_{\overline{\Omega}}|u_n(x)|$. If (4.15) is satisfied for ![]() $P_n^1$, then we get k = 1. It is evident that
$P_n^1$, then we get k = 1. It is evident that ![]() $P_n^1$ satisfies (4.13).
$P_n^1$ satisfies (4.13).
Otherwise, if ![]() $P_n^1$ does not satisfy (4.15), we suppose that there exists δ > 0 such that
$P_n^1$ does not satisfy (4.15), we suppose that there exists δ > 0 such that
 \begin{equation}
\lim_{R\to \infty}\left(\limsup_{n\to +\infty} \lambda_n^{-\frac{1}{p-2}} \max_{|x-P_n^1|\geq R\lambda_n^{-1/2}}|u_n(x)| \right)\geq 4\delta.
\end{equation}
\begin{equation}
\lim_{R\to \infty}\left(\limsup_{n\to +\infty} \lambda_n^{-\frac{1}{p-2}} \max_{|x-P_n^1|\geq R\lambda_n^{-1/2}}|u_n(x)| \right)\geq 4\delta.
\end{equation}For sufficiently large R, up to a subsequence, it holds
 \begin{equation}
\lambda_n^{-\frac{1}{p-2}} \max_{|x-P_n^1|\geq R\lambda_n^{-1/2}}|u_n(x)|\geq 2 \delta.
\end{equation}
\begin{equation}
\lambda_n^{-\frac{1}{p-2}} \max_{|x-P_n^1|\geq R\lambda_n^{-1/2}}|u_n(x)|\geq 2 \delta.
\end{equation} Let  $P_n^2\in \overline{\Omega}\backslash B_{R\lambda_n^{-1/2}}(P_n^1)$ such that
$P_n^2\in \overline{\Omega}\backslash B_{R\lambda_n^{-1/2}}(P_n^1)$ such that
 \begin{equation*}
|u_n(P_n^2)|=\max_{\overline{\Omega}\backslash B_{R\lambda_n^{-1/2}}(P_n^1)}|u_n|.
\end{equation*}
\begin{equation*}
|u_n(P_n^2)|=\max_{\overline{\Omega}\backslash B_{R\lambda_n^{-1/2}}(P_n^1)}|u_n|.
\end{equation*} Then, (4.17) yields that ![]() $|u_n(P_n^2)|\to +\infty$ as
$|u_n(P_n^2)|\to +\infty$ as ![]() $n\to +\infty$.
$n\to +\infty$.
We claim that
If (4.18) is not true, then up to subsequence  $\lambda_n^{\frac{1}{2}}|P_n^1-P_n^2|\to R'\geq R$. Define
$\lambda_n^{\frac{1}{2}}|P_n^1-P_n^2|\to R'\geq R$. Define
 \begin{equation*}
v_{n,1}(x):=a_0^{\frac{1}{p-2}}\lambda_n^{-\frac{1}{p-2}}u_n(\lambda_n^{-1/2}x + P_n^1).
\end{equation*}
\begin{equation*}
v_{n,1}(x):=a_0^{\frac{1}{p-2}}\lambda_n^{-\frac{1}{p-2}}u_n(\lambda_n^{-1/2}x + P_n^1).
\end{equation*} As in lemma 4.3, we can deduce that ![]() $ v_{n,1}\to v$ in
$ v_{n,1}\to v$ in ![]() $C^2_{loc}(\overline{D})$, where
$C^2_{loc}(\overline{D})$, where ![]() $D=\mathbb{R}^N$ or D is a half-space. Then, up to subsequences,
$D=\mathbb{R}^N$ or D is a half-space. Then, up to subsequences,
 \begin{equation*}
\lambda_n^{-\frac{1}{p-2}}u_n(P_n^2)=v_{n,1}(\lambda^{1/2}(P_n^2-P_n^1)) \to v(x'),~|x'|\geq R' \gt R.
\end{equation*}
\begin{equation*}
\lambda_n^{-\frac{1}{p-2}}u_n(P_n^2)=v_{n,1}(\lambda^{1/2}(P_n^2-P_n^1)) \to v(x'),~|x'|\geq R' \gt R.
\end{equation*} Since ![]() $v(x)\to 0$ as
$v(x)\to 0$ as ![]() $|x|\to \infty$, taking R larger if necessary, it follows that
$|x|\to \infty$, taking R larger if necessary, it follows that
 \begin{equation*}
|v(x)|\leq a_0^{\frac{1}{p-2}}\delta, ~\forall |x|\geq R.
\end{equation*}
\begin{equation*}
|v(x)|\leq a_0^{\frac{1}{p-2}}\delta, ~\forall |x|\geq R.
\end{equation*}This contradicts to (4.17), which proves the claim (4.18).
In the following, we shall show that
 \begin{equation}
|u_n(P_n^2)|=\max_{\overline{\Omega}\cap B_{R_{n,2}\lambda_n^{-1/2}}(P_n^2)}|u_n(x)|, ~{\rm for~some}~ R_{n,2}\to +\infty.
\end{equation}
\begin{equation}
|u_n(P_n^2)|=\max_{\overline{\Omega}\cap B_{R_{n,2}\lambda_n^{-1/2}}(P_n^2)}|u_n(x)|, ~{\rm for~some}~ R_{n,2}\to +\infty.
\end{equation} Let  $\tilde{\epsilon}_{n,2}=a_0^{-\frac{1}{2}}|u_n(P_n^2)|^{-\frac{p-2}{2}}$. Clearly,
$\tilde{\epsilon}_{n,2}=a_0^{-\frac{1}{2}}|u_n(P_n^2)|^{-\frac{p-2}{2}}$. Clearly, ![]() $\tilde{\epsilon}_{n,2}\to 0$. By (4.17), we get
$\tilde{\epsilon}_{n,2}\to 0$. By (4.17), we get  $\tilde{\epsilon}_{n,2}\leq (2\delta)^{-\frac{p-2}{2}}\lambda_n^{-\frac{1}{2}}$. From (4.18), we can assert that
$\tilde{\epsilon}_{n,2}\leq (2\delta)^{-\frac{p-2}{2}}\lambda_n^{-\frac{1}{2}}$. From (4.18), we can assert that
 \begin{equation*}
\tilde{R}_{n,2}:=\frac{|P_n^1-P_n^2|}{2\tilde{\epsilon}_{n,2}}\geq \frac{(2\delta)^{\frac{p-2}{2}}}{2}\lambda_n^{\frac{1}{2}}|P_n^1-P_n^2| \to +\infty~{\rm as }~n\to\infty.
\end{equation*}
\begin{equation*}
\tilde{R}_{n,2}:=\frac{|P_n^1-P_n^2|}{2\tilde{\epsilon}_{n,2}}\geq \frac{(2\delta)^{\frac{p-2}{2}}}{2}\lambda_n^{\frac{1}{2}}|P_n^1-P_n^2| \to +\infty~{\rm as }~n\to\infty.
\end{equation*} On the other hand, for any  $x\in B_{\tilde{R}_{n,2}\tilde{\epsilon}_{n,2}}(P_n^2)$ and R > 0, we have
$x\in B_{\tilde{R}_{n,2}\tilde{\epsilon}_{n,2}}(P_n^2)$ and R > 0, we have
 \begin{equation*}
|x-P_n^1|\geq |P_n^2-P_n^1|- |x-P_n^2|\geq \frac{1}{2}|P_n^2-P_n^1|\geq R\lambda_n^{-\frac{1}{2}}
\end{equation*}
\begin{equation*}
|x-P_n^1|\geq |P_n^2-P_n^1|- |x-P_n^2|\geq \frac{1}{2}|P_n^2-P_n^1|\geq R\lambda_n^{-\frac{1}{2}}
\end{equation*}for arbitrarily large n. Consequently,
 \begin{equation*}
\overline{\Omega}\cap B_{\tilde{R}_{n,2}\tilde{\epsilon}_{n,2}}(P_n^2)\subset \overline{\Omega}\backslash B_{R\lambda_n^{-\frac{1}{2}}}(P_n^1),
\end{equation*}
\begin{equation*}
\overline{\Omega}\cap B_{\tilde{R}_{n,2}\tilde{\epsilon}_{n,2}}(P_n^2)\subset \overline{\Omega}\backslash B_{R\lambda_n^{-\frac{1}{2}}}(P_n^1),
\end{equation*}which implies that
 \begin{equation}
|u_n(P_n^2)|=\max_{\overline{\Omega}\cap B_{\tilde{R}_{n,2}\tilde{\epsilon}_{n,2}}(P_n^2)}|u_n|.
\end{equation}
\begin{equation}
|u_n(P_n^2)|=\max_{\overline{\Omega}\cap B_{\tilde{R}_{n,2}\tilde{\epsilon}_{n,2}}(P_n^2)}|u_n|.
\end{equation}We define
 \begin{equation*}
\tilde{u}_{n,2}:=a_0^{\frac{1}{p-2}}\tilde{\epsilon}_{n,2}^{\frac{2}{p-2}}u_n(\tilde{\epsilon}_{n,2} x+P_n^2),~~~ x\in \tilde{\Omega}_{n,2}:=\frac{\Omega -P_n^2}{\tilde{\epsilon}_{n,2}}.
\end{equation*}
\begin{equation*}
\tilde{u}_{n,2}:=a_0^{\frac{1}{p-2}}\tilde{\epsilon}_{n,2}^{\frac{2}{p-2}}u_n(\tilde{\epsilon}_{n,2} x+P_n^2),~~~ x\in \tilde{\Omega}_{n,2}:=\frac{\Omega -P_n^2}{\tilde{\epsilon}_{n,2}}.
\end{equation*} Set ![]() $d_{n,2}={\rm dist} (P_n^2, \partial \Omega)$. Then, passing to subsequences if necessary,
$d_{n,2}={\rm dist} (P_n^2, \partial \Omega)$. Then, passing to subsequences if necessary,
 \begin{equation*}
\frac{\tilde{\epsilon}_{n,2}}{d_{n,2}}\to L_2\in [0,+\infty]~{\rm and}~\tilde{\Omega}_{n,2}\to
\begin{cases}
&\mathbb{R}^N ~~{\rm if}~~L_2=+\infty,\\
&\mathbb{H}~~{\rm if}~~L_2 \lt +\infty.
\end{cases}
\end{equation*}
\begin{equation*}
\frac{\tilde{\epsilon}_{n,2}}{d_{n,2}}\to L_2\in [0,+\infty]~{\rm and}~\tilde{\Omega}_{n,2}\to
\begin{cases}
&\mathbb{R}^N ~~{\rm if}~~L_2=+\infty,\\
&\mathbb{H}~~{\rm if}~~L_2 \lt +\infty.
\end{cases}
\end{equation*} Then ![]() $\tilde{u}_{n,2}$ satisfies the following equation
$\tilde{u}_{n,2}$ satisfies the following equation
 \begin{equation*}
\left\{\begin{array}{ll}
-\Delta \tilde{u}_{n,2}+ \lambda_n \tilde{\epsilon}_{n,2}^2 \tilde{u}_{n,2}=a_0^{\frac{1}{p-2}}\tilde{\epsilon}_{n,2}^{\frac{2p-2}{p-2}}h_{\rho_n}(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_{n,2}^{-\frac{2}{p-2}}\tilde{u}_{n,2}) & {\mathrm{in}} \,~ \tilde{\Omega}_{n,2},\\
|\tilde{u}_{n,2}(x)|\leq |\tilde{u}_{n,2}(0)|=1 & {\mathrm{in}} \,~ \tilde{\Omega}_{n,2}, \\
\displaystyle\frac{\partial \tilde{u}_{n,2}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial\tilde{\Omega}_{n,2}.
\end{array}\right.
\end{equation*}
\begin{equation*}
\left\{\begin{array}{ll}
-\Delta \tilde{u}_{n,2}+ \lambda_n \tilde{\epsilon}_{n,2}^2 \tilde{u}_{n,2}=a_0^{\frac{1}{p-2}}\tilde{\epsilon}_{n,2}^{\frac{2p-2}{p-2}}h_{\rho_n}(a_0^{-\frac{1}{p-2}}\tilde{\epsilon}_{n,2}^{-\frac{2}{p-2}}\tilde{u}_{n,2}) & {\mathrm{in}} \,~ \tilde{\Omega}_{n,2},\\
|\tilde{u}_{n,2}(x)|\leq |\tilde{u}_{n,2}(0)|=1 & {\mathrm{in}} \,~ \tilde{\Omega}_{n,2}, \\
\displaystyle\frac{\partial \tilde{u}_{n,2}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial\tilde{\Omega}_{n,2}.
\end{array}\right.
\end{equation*} Since ![]() $P_n^2$ is a local maximum or a local minimum point, by lemma 4.1, we get
$P_n^2$ is a local maximum or a local minimum point, by lemma 4.1, we get
 \begin{equation*}\frac{\lambda_n}{|u_n(P^2_n)|^{p-2}}\to \tilde{\lambda}^{(2)}\in [0, a_0],~{\rm as}~n\to \infty. \end{equation*}
\begin{equation*}\frac{\lambda_n}{|u_n(P^2_n)|^{p-2}}\to \tilde{\lambda}^{(2)}\in [0, a_0],~{\rm as}~n\to \infty. \end{equation*} Using the similar argument as in lemma 4.3, we deduce ![]() $\tilde{\lambda}^{(2)} \gt 0$, namely
$\tilde{\lambda}^{(2)} \gt 0$, namely
 \begin{equation*}
\lim_{n\to +\infty}\lambda_n^{\frac{1}{2}}\tilde{\epsilon}_{n,2} \gt 0.
\end{equation*}
\begin{equation*}
\lim_{n\to +\infty}\lambda_n^{\frac{1}{2}}\tilde{\epsilon}_{n,2} \gt 0.
\end{equation*}Set
 \begin{equation*}
v_{n,2}:=a_0^{\frac{1}{p-2}}\epsilon_n^{\frac{2}{p-2}} u_n(\epsilon_n x+P_n^2)~{\rm for }~x\in \Omega_{n,2}:=\frac{\Omega-P_n^2}{\epsilon_n},
\end{equation*}
\begin{equation*}
v_{n,2}:=a_0^{\frac{1}{p-2}}\epsilon_n^{\frac{2}{p-2}} u_n(\epsilon_n x+P_n^2)~{\rm for }~x\in \Omega_{n,2}:=\frac{\Omega-P_n^2}{\epsilon_n},
\end{equation*} where  $\epsilon_n=\lambda_n^{-\frac{1}{2}}$ is defined in (4.4). Up to a subsequence, there exists a function
$\epsilon_n=\lambda_n^{-\frac{1}{2}}$ is defined in (4.4). Up to a subsequence, there exists a function ![]() $v^{(2)}\in H^1(D)$ such that
$v^{(2)}\in H^1(D)$ such that ![]() $v_{n,2}\to v^{(2)}$ in
$v_{n,2}\to v^{(2)}$ in ![]() $C_{loc}^2(\overline{D})$, where D is either
$C_{loc}^2(\overline{D})$, where D is either ![]() $\mathbb{R}^N$ or a half space. Moreover,
$\mathbb{R}^N$ or a half space. Moreover, ![]() $v^{(2)}$ solves the following problem
$v^{(2)}$ solves the following problem
 \begin{equation}
\left\{\begin{array}{ll}
-\Delta v^{(2)}+ v^{(2)}=|v^{(2)}|^{p-2}v^{(2)} & {\mathrm{in}} \,~ D,\\
|v^{(2)}(x)|\leq |v^{(2)}(0)|= (\tilde{\lambda}^{(2)})^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ D, \\
\displaystyle\frac{\partial v^{(2)}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D.
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta v^{(2)}+ v^{(2)}=|v^{(2)}|^{p-2}v^{(2)} & {\mathrm{in}} \,~ D,\\
|v^{(2)}(x)|\leq |v^{(2)}(0)|= (\tilde{\lambda}^{(2)})^{-\frac{1}{p-2}} & {\mathrm{in}} \,~ D, \\
\displaystyle\frac{\partial v^{(2)}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D.
\end{array}\right.
\end{equation} Then, by a similar discussion as above, we conclude that either  $\frac{d_{n,2}}{\epsilon_n}\to +\infty$ or
$\frac{d_{n,2}}{\epsilon_n}\to +\infty$ or  $\frac{d_{n,2}}{\epsilon_n}$ remains bounded. Define
$\frac{d_{n,2}}{\epsilon_n}$ remains bounded. Define  $R_{n,2}= \tilde{R}_{n,2}\lambda_n^{\frac{1}{2}}\tilde{\epsilon}_{n,2}$. Clearly,
$R_{n,2}= \tilde{R}_{n,2}\lambda_n^{\frac{1}{2}}\tilde{\epsilon}_{n,2}$. Clearly, ![]() $ R_{n,2}\to +\infty$ as
$ R_{n,2}\to +\infty$ as ![]() $n\to+\infty$. Hence, (4.19) holds.
$n\to+\infty$. Hence, (4.19) holds.
If (4.15) does not hold, we can apply similar arguments as before to show that there exists ![]() $P_n^3$ such that (4.13)–(4.14) are satisfied. For
$P_n^3$ such that (4.13)–(4.14) are satisfied. For ![]() $P_n^i,i=1,2,3$, applying lemma 4.3 again, we can find
$P_n^i,i=1,2,3$, applying lemma 4.3 again, we can find ![]() $\phi^i_n\in C^\infty_0(\Omega)$ with supp
$\phi^i_n\in C^\infty_0(\Omega)$ with supp![]() $\phi^i_n\subset B_{R\varepsilon_n}(P_n^i)\cap \overline{\Omega}$ for some R > 0, such that
$\phi^i_n\subset B_{R\varepsilon_n}(P_n^i)\cap \overline{\Omega}$ for some R > 0, such that
 \begin{equation*}
\int_\Omega\vert \nabla\phi^i_n\vert~^2dx+\int_\Omega[(\lambda-(p-1)\rho_nu_n^{p-2})(\phi^i_n)^2]dx \lt 0.
\end{equation*}
\begin{equation*}
\int_\Omega\vert \nabla\phi^i_n\vert~^2dx+\int_\Omega[(\lambda-(p-1)\rho_nu_n^{p-2})(\phi^i_n)^2]dx \lt 0.
\end{equation*} In light of (4.14), we observe that ![]() $\phi^1_n,\phi^2_n,\phi_n^{3}$ are mutually orthogonal for sufficiently large n, which implies
$\phi^1_n,\phi^2_n,\phi_n^{3}$ are mutually orthogonal for sufficiently large n, which implies  $\lim\limits_{n\rightarrow+\infty}m(u_n)\ge3$. This leads to a contradiction with the fact that
$\lim\limits_{n\rightarrow+\infty}m(u_n)\ge3$. This leads to a contradiction with the fact that ![]() $m(u_n)\leq2$.
$m(u_n)\leq2$.
In the subsequent analysis, we show that un exhibits exponential decay away from the blow-up points.
Lemma 4.5. Let ![]() $\{P_n^1\},\ldots,\{P_n^k\}$ be given in lemma 4.4. Then there exist constants
$\{P_n^1\},\ldots,\{P_n^k\}$ be given in lemma 4.4. Then there exist constants ![]() $C_1 \gt 0$,
$C_1 \gt 0$, ![]() $C_2 \gt 0$ such that, for some R > 0,
$C_2 \gt 0$ such that, for some R > 0,
 \begin{equation}
u_n(x)\leq C_1e^{C_1 R}\lambda_n^{\frac{1}{p-2}}\sum_{i=1}^k e^{-C_2\lambda_n^{\frac{1}{2}}|x-P_n^i|}, ~\forall x\in \overline{\Omega}\backslash \cup_{i=1}^k (B_{R\lambda_n^{-\frac{1}{2}}}(P_n^i)\cap \overline{\Omega}).
\end{equation}
\begin{equation}
u_n(x)\leq C_1e^{C_1 R}\lambda_n^{\frac{1}{p-2}}\sum_{i=1}^k e^{-C_2\lambda_n^{\frac{1}{2}}|x-P_n^i|}, ~\forall x\in \overline{\Omega}\backslash \cup_{i=1}^k (B_{R\lambda_n^{-\frac{1}{2}}}(P_n^i)\cap \overline{\Omega}).
\end{equation}Proof. The proof is inspired by [Reference Li and Zhao38, lemma 2.1] and [Reference Esposito and Petralla20, theorem 3.2]. For any θ > 0, we set
and define the inner normal bundle
where νx is the unit outer normal of ![]() $\partial\Omega$ at x.
$\partial\Omega$ at x.
Since ![]() $\partial\Omega$ is a smooth compact submanifold of
$\partial\Omega$ is a smooth compact submanifold of ![]() $\mathbb{R}^N$, by the tubular neighbourhood theorem, it follows that there exists a diffeomorphism
$\mathbb{R}^N$, by the tubular neighbourhood theorem, it follows that there exists a diffeomorphism ![]() $\Phi_{Ib}$ from
$\Phi_{Ib}$ from ![]() $\Omega_\theta$ onto
$\Omega_\theta$ onto ![]() $(\partial\Omega)_\theta$. More precisely, for any
$(\partial\Omega)_\theta$. More precisely, for any ![]() $x\in \Omega_\theta$, it is easily seen that there exists a unique
$x\in \Omega_\theta$, it is easily seen that there exists a unique ![]() $\bar{x}\in \partial\Omega$ such that
$\bar{x}\in \partial\Omega$ such that ![]() ${\rm dist}(x, \bar{x})= {\rm dist}(x, \partial\Omega)$. Hence, we can define
${\rm dist}(x, \bar{x})= {\rm dist}(x, \partial\Omega)$. Hence, we can define ![]() $\Phi_{Ib}(x):=(\bar{x}, -{\rm dist}(x, \bar{x})\nu_{\bar{x}})$ for any
$\Phi_{Ib}(x):=(\bar{x}, -{\rm dist}(x, \bar{x})\nu_{\bar{x}})$ for any ![]() $x\in \Omega_\theta$. Clearly,
$x\in \Omega_\theta$. Clearly, ![]() $\Phi_{Ib}(x)=x$ for
$\Phi_{Ib}(x)=x$ for ![]() $x\in \partial\Omega$.
$x\in \partial\Omega$.
Similarly, let
and define the outer normal bundle
Then there exists a diffeomorphism ![]() $\Phi_{Ob}:\Omega^\theta \to (\partial\Omega)^\theta$ defined by
$\Phi_{Ob}:\Omega^\theta \to (\partial\Omega)^\theta$ defined by ![]() $\Phi_{Ob}(x):=(\hat{x}, dist(x, \hat{x})\nu_{\hat{x}}), \forall x\in \Omega^\theta $. Here
$\Phi_{Ob}(x):=(\hat{x}, dist(x, \hat{x})\nu_{\hat{x}}), \forall x\in \Omega^\theta $. Here ![]() $\hat{x}\in \partial\Omega$ is the unique element in
$\hat{x}\in \partial\Omega$ is the unique element in ![]() $\partial \Omega$ such that
$\partial \Omega$ such that ![]() ${\rm dist}(x, \hat{x})= {\rm dist}(x, \partial\Omega)$. Moreover,
${\rm dist}(x, \hat{x})= {\rm dist}(x, \partial\Omega)$. Moreover, ![]() $\Phi_{Ob}|_{\partial\Omega}= {\rm Identity}$.
$\Phi_{Ob}|_{\partial\Omega}= {\rm Identity}$.
Consider the reflection ![]() $\Phi_C:(\partial\Omega)_\theta\to (\partial\Omega)^\theta$ defined by
$\Phi_C:(\partial\Omega)_\theta\to (\partial\Omega)^\theta$ defined by ![]() $\Phi_C((x,y)):=(x,-y)$. Then,
$\Phi_C((x,y)):=(x,-y)$. Then,  $\Phi:=\Phi_{Ib}^{-1}\circ \Phi_C^{-1}\circ \Phi_{Ob}$ is a diffeomorphism from
$\Phi:=\Phi_{Ib}^{-1}\circ \Phi_C^{-1}\circ \Phi_{Ob}$ is a diffeomorphism from ![]() $\Omega^\theta$ onto
$\Omega^\theta$ onto ![]() $\Omega_\theta$ and
$\Omega_\theta$ and ![]() $\Phi |_{\partial\Omega}={\rm Identity}$. Furthermore, we take
$\Phi |_{\partial\Omega}={\rm Identity}$. Furthermore, we take ![]() $x=\Phi(z)=(\Phi_1(z),\ldots,\Phi_N(z))$ for
$x=\Phi(z)=(\Phi_1(z),\ldots,\Phi_N(z))$ for ![]() $z\in\Omega^\theta$,
$z\in\Omega^\theta$, ![]() $z=\Psi(x)=\Phi^{-1}(x)=(\Psi_1(x),\ldots,\Psi_N(x))$ for
$z=\Psi(x)=\Phi^{-1}(x)=(\Psi_1(x),\ldots,\Psi_N(x))$ for ![]() $x\in \Omega_\theta$, and
$x\in \Omega_\theta$, and
 \begin{equation*}
g_{ij}= \sum_{l=1}^N \frac{\partial \Phi_l}{\partial z_i}\frac{\partial \Phi_l}{\partial z_j},~~
g^{ij}= \sum_{l=1}^n \frac{\partial \Psi_i}{\partial x_l}\frac{\partial \Psi_j}{\partial x_l}(\Phi (z)).
\end{equation*}
\begin{equation*}
g_{ij}= \sum_{l=1}^N \frac{\partial \Phi_l}{\partial z_i}\frac{\partial \Phi_l}{\partial z_j},~~
g^{ij}= \sum_{l=1}^n \frac{\partial \Psi_i}{\partial x_l}\frac{\partial \Psi_j}{\partial x_l}(\Phi (z)).
\end{equation*} Then ![]() $g_{ij}|_{\partial \Omega}= g^{ij}|_{\partial\Omega}=\delta_{ij}$, where δij is the Kronecker symbol. For simplicity, denote
$g_{ij}|_{\partial \Omega}= g^{ij}|_{\partial\Omega}=\delta_{ij}$, where δij is the Kronecker symbol. For simplicity, denote ![]() $G=(g^{ij})$,
$G=(g^{ij})$, ![]() $g(x)=det(g_{ij})$ and
$g(x)=det(g_{ij})$ and ![]() $\hat{u}_n(x)=u_n(\Phi(x))$ for
$\hat{u}_n(x)=u_n(\Phi(x))$ for ![]() $x\in \Omega^\theta$. Then
$x\in \Omega^\theta$. Then ![]() $\hat{u}_n$ satisfies
$\hat{u}_n$ satisfies
 \begin{equation*}
\left\{\begin{array}{ll}
-L \hat{u}_n+ \sqrt{g}\lambda_n \hat{u}_n=\sqrt{g}h_{\rho_n}(\hat{u}_n) & {\mathrm{in}} \,~ \Omega^\theta,\\
\displaystyle\frac{\partial \hat{u}_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,
\end{array}\right.
\end{equation*}
\begin{equation*}
\left\{\begin{array}{ll}
-L \hat{u}_n+ \sqrt{g}\lambda_n \hat{u}_n=\sqrt{g}h_{\rho_n}(\hat{u}_n) & {\mathrm{in}} \,~ \Omega^\theta,\\
\displaystyle\frac{\partial \hat{u}_n}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial \Omega,
\end{array}\right.
\end{equation*}where
 \begin{equation*}L \hat{u}_n= \sum_{i=1}^N \frac{\partial}{\partial x_i}\left(\sqrt{g}\sum_{j=1}^Ng^{ij}\frac{\partial \hat{u}_n}{\partial x_j}\right). \end{equation*}
\begin{equation*}L \hat{u}_n= \sum_{i=1}^N \frac{\partial}{\partial x_i}\left(\sqrt{g}\sum_{j=1}^Ng^{ij}\frac{\partial \hat{u}_n}{\partial x_j}\right). \end{equation*}Next we define
 \begin{equation*}
\bar{u}_n:=
\begin{cases}
u_n(x), x\in\Omega,\\
\hat{u}_n(x), x\in \Omega^\theta,
\end{cases}
\bar{g}_{ij}:=
\begin{cases}
\delta_{ij}, x\in \bar\Omega,\\
g_{ij}, x\in \Omega^\theta,
\end{cases}
\bar{g}^{ij}:=
\begin{cases}
\delta_{ij}, x\in \bar\Omega,\\
g^{ij}, x\in \Omega^\theta,
\end{cases}
\end{equation*}
\begin{equation*}
\bar{u}_n:=
\begin{cases}
u_n(x), x\in\Omega,\\
\hat{u}_n(x), x\in \Omega^\theta,
\end{cases}
\bar{g}_{ij}:=
\begin{cases}
\delta_{ij}, x\in \bar\Omega,\\
g_{ij}, x\in \Omega^\theta,
\end{cases}
\bar{g}^{ij}:=
\begin{cases}
\delta_{ij}, x\in \bar\Omega,\\
g^{ij}, x\in \Omega^\theta,
\end{cases}
\end{equation*} and ![]() $\bar{g}:= det(\bar{g}_{ij})$. Let
$\bar{g}:= det(\bar{g}_{ij})$. Let ![]() $A(x, \xi)=(A_1(x, \xi),\ldots,A_N(x, \xi))$ for
$A(x, \xi)=(A_1(x, \xi),\ldots,A_N(x, \xi))$ for ![]() $\xi=(\xi_1,\ldots,\xi_N)$ with
$\xi=(\xi_1,\ldots,\xi_N)$ with
 \begin{equation*}A_i(x,\xi)=\sqrt{\bar{g}}\sum_{j=1}^N\bar{g}^{ij}\xi_j.\end{equation*}
\begin{equation*}A_i(x,\xi)=\sqrt{\bar{g}}\sum_{j=1}^N\bar{g}^{ij}\xi_j.\end{equation*} Then ![]() $\bar{u}_n$ weakly solves
$\bar{u}_n$ weakly solves
 \begin{equation}
-div\left(A(x,\nabla \bar{u}_n)\right)+ \lambda_n \sqrt{\bar{g}}\bar{u}_n= \sqrt{\bar{g}} g_{\rho_n}(\bar{u}_n)~~{\mathrm{in}}~~\overline{\Omega}\cup \Omega^\theta.
\end{equation}
\begin{equation}
-div\left(A(x,\nabla \bar{u}_n)\right)+ \lambda_n \sqrt{\bar{g}}\bar{u}_n= \sqrt{\bar{g}} g_{\rho_n}(\bar{u}_n)~~{\mathrm{in}}~~\overline{\Omega}\cup \Omega^\theta.
\end{equation} Given that Φ is a diffeomorphism, the functions  $g_{ij}(x), \frac{\partial g_{ii}}{\partial x_i}$ and
$g_{ij}(x), \frac{\partial g_{ii}}{\partial x_i}$ and  $\frac{\partial g_{ij}}{\partial x_i}$ are all smooth on the domain
$\frac{\partial g_{ij}}{\partial x_i}$ are all smooth on the domain ![]() $\Omega^\theta$. Consequently, there exists a constant
$\Omega^\theta$. Consequently, there exists a constant ![]() $C_0 \gt 0$ such that
$C_0 \gt 0$ such that  $|\frac{\partial g_{ii}}{\partial x_i}|, |\frac{\partial g_{ij}}{\partial x_i}|\leq C_0$ are both bounded by C 0 for
$|\frac{\partial g_{ii}}{\partial x_i}|, |\frac{\partial g_{ij}}{\partial x_i}|\leq C_0$ are both bounded by C 0 for ![]() $x\in \Omega^\theta$. Moreover, according to the Taylor expansion, as θ approaches 0, the functions gij and g ij tend to 0, while gii and g ii tend to 1, and the determinant g(x) converges to 1.
$x\in \Omega^\theta$. Moreover, according to the Taylor expansion, as θ approaches 0, the functions gij and g ij tend to 0, while gii and g ii tend to 1, and the determinant g(x) converges to 1.
For any ![]() $\tilde{x}\in \overline{\Omega}$, there exists β > 0 such that
$\tilde{x}\in \overline{\Omega}$, there exists β > 0 such that ![]() $B_\beta (\tilde{x})\subset \overline{\Omega}\cup \Omega^\theta$. For
$B_\beta (\tilde{x})\subset \overline{\Omega}\cup \Omega^\theta$. For ![]() $x\in B_\beta(\tilde{x})\backslash \tilde{x}$, denote
$x\in B_\beta(\tilde{x})\backslash \tilde{x}$, denote ![]() $\sigma= |x-\tilde{x}|$. Then, for any smooth increasing function
$\sigma= |x-\tilde{x}|$. Then, for any smooth increasing function ![]() $\phi(\sigma)$, we have
$\phi(\sigma)$, we have
 \begin{align*}
\left|\sum_{i=1}^N \frac{\partial}{\partial x_i}(\sqrt{g}g^{ij})\frac{\partial \phi}{\partial x_j}\right|&= \left|\sum_{i=1}^N \frac{\partial}{\partial x_i}(\sqrt{g}g^{ij}) \frac{x_j-\tilde{x}_j}{\sigma} \phi'\right|\\
&\leq\sum_{i=1}^N \bigg| \max_{x\in \overline{\Omega}\cup \Omega^\theta} \frac{\partial}{\partial x_i}(\sqrt{g}g^{ij}) \bigg|\phi' \frac{diam(\overline{\Omega}\cup \Omega^\theta)}{\sigma}\\
&\le \frac{C_{\Phi ,\Omega}\phi'}{\sigma}
\end{align*}
\begin{align*}
\left|\sum_{i=1}^N \frac{\partial}{\partial x_i}(\sqrt{g}g^{ij})\frac{\partial \phi}{\partial x_j}\right|&= \left|\sum_{i=1}^N \frac{\partial}{\partial x_i}(\sqrt{g}g^{ij}) \frac{x_j-\tilde{x}_j}{\sigma} \phi'\right|\\
&\leq\sum_{i=1}^N \bigg| \max_{x\in \overline{\Omega}\cup \Omega^\theta} \frac{\partial}{\partial x_i}(\sqrt{g}g^{ij}) \bigg|\phi' \frac{diam(\overline{\Omega}\cup \Omega^\theta)}{\sigma}\\
&\le \frac{C_{\Phi ,\Omega}\phi'}{\sigma}
\end{align*} for some ![]() $C_{\Phi ,\Omega} \gt 0$, where
$C_{\Phi ,\Omega} \gt 0$, where  $\phi'=\frac{d\phi(\sigma)}{d\sigma}$. Moreover, for θ > 0 small enough, there exist small constants
$\phi'=\frac{d\phi(\sigma)}{d\sigma}$. Moreover, for θ > 0 small enough, there exist small constants ![]() $\delta_0, \delta_1$ such that
$\delta_0, \delta_1$ such that
 \begin{align*}
\left|\sqrt{g} g^{ii}\frac{\partial^2 \phi}{\partial x_i^2}\right|
&=\left|\sqrt{g} g^{ii} \left(\frac{\phi'}{\sigma}+\phi^{\prime\prime}\frac{(x_i-\tilde{x}_i)^2}{\sigma^2}- \phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right) \right|\\
&\leq (1+\delta_0) \left(\frac{\phi'}{\sigma}+ |\phi^{\prime\prime}|\frac{(x_i-\tilde{x}_i)^2}{\sigma^2}+\phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right),
\end{align*}
\begin{align*}
\left|\sqrt{g} g^{ii}\frac{\partial^2 \phi}{\partial x_i^2}\right|
&=\left|\sqrt{g} g^{ii} \left(\frac{\phi'}{\sigma}+\phi^{\prime\prime}\frac{(x_i-\tilde{x}_i)^2}{\sigma^2}- \phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right) \right|\\
&\leq (1+\delta_0) \left(\frac{\phi'}{\sigma}+ |\phi^{\prime\prime}|\frac{(x_i-\tilde{x}_i)^2}{\sigma^2}+\phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right),
\end{align*}and
 \begin{equation*}
\begin{aligned}
\left|\sqrt{g} g^{ij}\frac{\partial^2 \phi}{\partial x_j \partial x_i}\right|
&=\left| \sqrt{g} g^{ij} \left(\phi^{\prime\prime}\frac{(x_i-\tilde{x}_i)(x_j-\tilde{x}_j)}{\sigma^2}- \phi'\frac{(x_i-\tilde{x}_i)(x_j-\tilde{x}_j)}{\sigma^3}\right) \right|\\
&\leq |\sqrt{g} g^{ij}| \left(\frac{1}{2} |\phi^{\prime\prime}| \frac{(x_i-\tilde{x}_i)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right)\\
&+|\sqrt{g} g^{ij}|\left(\frac{1}{2} |\phi^{\prime\prime}|\frac{(x_j-\tilde{x}_j)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_j-\tilde{x}_j)^2}{\sigma^3}\right)\\
&\leq \delta_1 \left(\frac{1}{2} |\phi^{\prime\prime}| \frac{(x_i-\tilde{x}_i)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right)\\
&+\delta_1 \left(\frac{1}{2} |\phi^{\prime\prime}|\frac{(x_j-\tilde{x}_j)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_j-\tilde{x}_j)^2}{\sigma^3}\right), ~{\rm for}~ i\not= j.
\end{aligned}
\end{equation*}
\begin{equation*}
\begin{aligned}
\left|\sqrt{g} g^{ij}\frac{\partial^2 \phi}{\partial x_j \partial x_i}\right|
&=\left| \sqrt{g} g^{ij} \left(\phi^{\prime\prime}\frac{(x_i-\tilde{x}_i)(x_j-\tilde{x}_j)}{\sigma^2}- \phi'\frac{(x_i-\tilde{x}_i)(x_j-\tilde{x}_j)}{\sigma^3}\right) \right|\\
&\leq |\sqrt{g} g^{ij}| \left(\frac{1}{2} |\phi^{\prime\prime}| \frac{(x_i-\tilde{x}_i)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right)\\
&+|\sqrt{g} g^{ij}|\left(\frac{1}{2} |\phi^{\prime\prime}|\frac{(x_j-\tilde{x}_j)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_j-\tilde{x}_j)^2}{\sigma^3}\right)\\
&\leq \delta_1 \left(\frac{1}{2} |\phi^{\prime\prime}| \frac{(x_i-\tilde{x}_i)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_i-\tilde{x}_i)^2}{\sigma^3}\right)\\
&+\delta_1 \left(\frac{1}{2} |\phi^{\prime\prime}|\frac{(x_j-\tilde{x}_j)^2}{\sigma^2}+ \frac{1}{2}\phi'\frac{(x_j-\tilde{x}_j)^2}{\sigma^3}\right), ~{\rm for}~ i\not= j.
\end{aligned}
\end{equation*}Then
 \begin{equation}
\left|\sum_{i=1}^N \frac{\partial}{\partial x_i}\left(\sqrt{g}\sum_{j=1}^Ng^{ij}\frac{\partial \phi}{\partial x_j}\right)\right|
\leq 2 |\phi^{\prime\prime}| + \frac{2(N-1)}{\sigma}\phi' + \frac{C_{\Phi ,\Omega}\phi'}{\sigma}.
\end{equation}
\begin{equation}
\left|\sum_{i=1}^N \frac{\partial}{\partial x_i}\left(\sqrt{g}\sum_{j=1}^Ng^{ij}\frac{\partial \phi}{\partial x_j}\right)\right|
\leq 2 |\phi^{\prime\prime}| + \frac{2(N-1)}{\sigma}\phi' + \frac{C_{\Phi ,\Omega}\phi'}{\sigma}.
\end{equation} From now, let us fix ![]() $\theta_*\in (0, \theta)$ such that
$\theta_*\in (0, \theta)$ such that  $\frac{1}{2}\leq\sqrt{g}\leq \frac{3}{2}$ and (4.24) holds. Define
$\frac{1}{2}\leq\sqrt{g}\leq \frac{3}{2}$ and (4.24) holds. Define
 \begin{equation*}
A_n^*:=\{x\in \overline{\Omega}\cup \Omega^{\theta_*}: d_n(x)\geq R\lambda_n^{-1/2}\}.
\end{equation*}
\begin{equation*}
A_n^*:=\{x\in \overline{\Omega}\cup \Omega^{\theta_*}: d_n(x)\geq R\lambda_n^{-1/2}\}.
\end{equation*} In view of (4.5), for every ![]() $\epsilon\in (0,1)$ small, to be chosen later, there exist
$\epsilon\in (0,1)$ small, to be chosen later, there exist ![]() $R^* \gt 0$ and
$R^* \gt 0$ and ![]() $n_R\in \mathbb{N}$ large such that
$n_R\in \mathbb{N}$ large such that
 \begin{equation*}
\max_{\{x\in \overline{\Omega} : d_n(x)\geq R\lambda_n^{-1/2}\}}|u_n|\leq \lambda_n^{\frac{1}{p-2}}\epsilon,~\forall R \gt R^*, ~ \forall n\geq n_R.
\end{equation*}
\begin{equation*}
\max_{\{x\in \overline{\Omega} : d_n(x)\geq R\lambda_n^{-1/2}\}}|u_n|\leq \lambda_n^{\frac{1}{p-2}}\epsilon,~\forall R \gt R^*, ~ \forall n\geq n_R.
\end{equation*} Let  $A_n: =\{x\in \overline{\Omega}: d_n(x)\geq R\lambda_n^{-1/2}\}$. Clearly,
$A_n: =\{x\in \overline{\Omega}: d_n(x)\geq R\lambda_n^{-1/2}\}$. Clearly,
Note that there exists a constant ![]() $n_\theta \gt 0$ large enough such that for
$n_\theta \gt 0$ large enough such that for ![]() $n \gt n_\theta$, for any
$n \gt n_\theta$, for any ![]() $i\in \{1,\ldots, k\}$, we have
$i\in \{1,\ldots, k\}$, we have  $B_{\lambda_n^{-1/2}R}(P_n^i)\subset \Omega^{\theta_*}\cup \Omega_{\theta_*}$. Then we can deduce that
$B_{\lambda_n^{-1/2}R}(P_n^i)\subset \Omega^{\theta_*}\cup \Omega_{\theta_*}$. Then we can deduce that ![]() $A_n\subset A_n^*$, for
$A_n\subset A_n^*$, for ![]() $n \gt \max\{n_\theta, n_R\}:= n_{\theta R}$. From the definition of
$n \gt \max\{n_\theta, n_R\}:= n_{\theta R}$. From the definition of ![]() $\bar{u}_n$, we get
$\bar{u}_n$, we get
Using ![]() $(f_1)$–
$(f_1)$–![]() $(f_2)$, we conclude that
$(f_2)$, we conclude that
 \begin{equation}
-div\left(A(x,\nabla \bar{u}_n)\right)+ \frac{\lambda_n}{2}\bar{u}_n\leq 0, ~\forall x\in A_n^*
\end{equation}
\begin{equation}
-div\left(A(x,\nabla \bar{u}_n)\right)+ \frac{\lambda_n}{2}\bar{u}_n\leq 0, ~\forall x\in A_n^*
\end{equation}holds for sufficiently small ϵ > 0.
For any ![]() $x_0\in A_n$ such that
$x_0\in A_n$ such that ![]() $B_r(x_0)\subset A_n^*$, consider the function
$B_r(x_0)\subset A_n^*$, consider the function
 \begin{equation*}
\phi_n(\sigma)=\phi_n(|x-x_0|)=\lambda_n^{\frac{1}{p-2}}\frac{\cosh{(\gamma \lambda_n^{\frac{1}{2}}\sigma})}{\cosh{(\gamma \lambda_n^{\frac{1}{2}}r})}.
\end{equation*}
\begin{equation*}
\phi_n(\sigma)=\phi_n(|x-x_0|)=\lambda_n^{\frac{1}{p-2}}\frac{\cosh{(\gamma \lambda_n^{\frac{1}{2}}\sigma})}{\cosh{(\gamma \lambda_n^{\frac{1}{2}}r})}.
\end{equation*} Clearly, ![]() $\phi'(\rho) \gt 0$ and
$\phi'(\rho) \gt 0$ and ![]() $\phi^{\prime\prime}(\rho) \gt 0$. By direct computations, we obtain
$\phi^{\prime\prime}(\rho) \gt 0$. By direct computations, we obtain
 \begin{equation}
\begin{aligned}
& 2|\phi_n^{\prime\prime}|+\frac{2(N-1)}{\sigma}\phi_n'+ \frac{C_{\Phi,\Omega}}{\sigma}\phi_n'- \frac{\lambda_n}{2}\phi_n\\
&=\lambda_n\phi_n \left(2\gamma^2+ (2(N-1)+C_{\Phi,\Omega})\gamma^2 \frac{\tanh{(\gamma \lambda_n^{\frac{1}{2}}\sigma)}}{\gamma\lambda_n^{\frac{1}{2}}\sigma}-\frac{1}{2} \right)\\
&\leq \lambda_n\phi_n \left(2\gamma^2+ (2(N-1)+C_{\Phi,\Omega})\gamma^2 -\frac{1}{2} \right)\leq 0,
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& 2|\phi_n^{\prime\prime}|+\frac{2(N-1)}{\sigma}\phi_n'+ \frac{C_{\Phi,\Omega}}{\sigma}\phi_n'- \frac{\lambda_n}{2}\phi_n\\
&=\lambda_n\phi_n \left(2\gamma^2+ (2(N-1)+C_{\Phi,\Omega})\gamma^2 \frac{\tanh{(\gamma \lambda_n^{\frac{1}{2}}\sigma)}}{\gamma\lambda_n^{\frac{1}{2}}\sigma}-\frac{1}{2} \right)\\
&\leq \lambda_n\phi_n \left(2\gamma^2+ (2(N-1)+C_{\Phi,\Omega})\gamma^2 -\frac{1}{2} \right)\leq 0,
\end{aligned}
\end{equation} for any ![]() $\gamma\in (0, \gamma_*]$, where
$\gamma\in (0, \gamma_*]$, where  $\gamma_*=(4N+2C_{\Phi,\Omega})^{-\frac{1}{2}}$. Then, fixing
$\gamma_*=(4N+2C_{\Phi,\Omega})^{-\frac{1}{2}}$. Then, fixing ![]() $\gamma\in (0, \gamma_*]$, by (4.24) and (4.26) it follows that
$\gamma\in (0, \gamma_*]$, by (4.24) and (4.26) it follows that
 \begin{equation}
\begin{aligned}
div(A(x, \nabla \phi_n))-\frac{\lambda_n}{2}\phi_n =\sum_{i=1}^N \frac{\partial}{\partial x_i}\left(\sqrt{\bar{g}}\sum_{j=1}^N\bar{g}^{ij}\frac{\partial \phi}{\partial x_j}\right)-\frac{\lambda_n}{2}\phi_n
\leq 0, ~\forall x\in B_r(x_0).
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
div(A(x, \nabla \phi_n))-\frac{\lambda_n}{2}\phi_n =\sum_{i=1}^N \frac{\partial}{\partial x_i}\left(\sqrt{\bar{g}}\sum_{j=1}^N\bar{g}^{ij}\frac{\partial \phi}{\partial x_j}\right)-\frac{\lambda_n}{2}\phi_n
\leq 0, ~\forall x\in B_r(x_0).
\end{aligned}
\end{equation} In addition, for ![]() $x\in \partial B_r(x_0)$, we have
$x\in \partial B_r(x_0)$, we have  $\left(\phi_n -\bar{u}_n \right) \geq \lambda_n^{\frac{1}{p-2}}(1-\epsilon) \gt 0$. Then, together with (4.25) and (4.27), by the comparison principle ([Reference Pucci and Serrin52, theorem 10.1]) it follows that
$\left(\phi_n -\bar{u}_n \right) \geq \lambda_n^{\frac{1}{p-2}}(1-\epsilon) \gt 0$. Then, together with (4.25) and (4.27), by the comparison principle ([Reference Pucci and Serrin52, theorem 10.1]) it follows that ![]() $\bar{u}_n\leq \phi_n~~{\mathrm{in}}~~B_r(x_0)$, which implies that
$\bar{u}_n\leq \phi_n~~{\mathrm{in}}~~B_r(x_0)$, which implies that  $u_n(x_0)\leq \lambda_n^{\frac{1}{p-2}} e^{-\gamma\lambda_n^{\frac{1}{2}}r}$.
$u_n(x_0)\leq \lambda_n^{\frac{1}{p-2}} e^{-\gamma\lambda_n^{\frac{1}{2}}r}$.
Take ![]() $r={\rm dist}(x_0, \partial A_n^*)$. We distinguish the following two cases:
$r={\rm dist}(x_0, \partial A_n^*)$. We distinguish the following two cases:
(i)
 $dist(x_0, \partial A_n^*)= dist(x_0, B_{R\lambda_n^{-1/2}}(P_n^i))$ for some
$dist(x_0, \partial A_n^*)= dist(x_0, B_{R\lambda_n^{-1/2}}(P_n^i))$ for some  $i\in \{1,\ldots,k\}$;
$i\in \{1,\ldots,k\}$;(ii)
 $dist(x_0, \partial A_n^*)= dist(x_0, \partial(\overline{\Omega}\cup \Omega^{\theta_*}))$.
$dist(x_0, \partial A_n^*)= dist(x_0, \partial(\overline{\Omega}\cup \Omega^{\theta_*}))$.
For case (i), we have  $|x_0- P_n^i|= r+ R\lambda_n^{-\frac{1}{2}}$. Then
$|x_0- P_n^i|= r+ R\lambda_n^{-\frac{1}{2}}$. Then
 \begin{equation*}u_n(x_0)\leq e^{\gamma R}\lambda_n^{\frac{1}{p-2}} e^{-\gamma\lambda_n^{\frac{1}{2}}r- \gamma R}=e^{\gamma R}\lambda_n^{\frac{1}{p-2}} e^{-\gamma \lambda_n^{\frac{1}{2}}|x_0-P_n^i|}.\end{equation*}
\begin{equation*}u_n(x_0)\leq e^{\gamma R}\lambda_n^{\frac{1}{p-2}} e^{-\gamma\lambda_n^{\frac{1}{2}}r- \gamma R}=e^{\gamma R}\lambda_n^{\frac{1}{p-2}} e^{-\gamma \lambda_n^{\frac{1}{2}}|x_0-P_n^i|}.\end{equation*}For case (ii), we deduce that
 \begin{equation*}u_n(x_0)\leq \lambda_n^{\frac{1}{p-2}} e^{-\gamma \lambda_n^{\frac{1}{2}}\theta_*}\leq \lambda_n^{\frac{1}{p-2}} e^{-\gamma \lambda_n^{\frac{1}{2}} \frac{\theta_*}{diam (\Omega)}|x_0-P_n^i|}.\end{equation*}
\begin{equation*}u_n(x_0)\leq \lambda_n^{\frac{1}{p-2}} e^{-\gamma \lambda_n^{\frac{1}{2}}\theta_*}\leq \lambda_n^{\frac{1}{p-2}} e^{-\gamma \lambda_n^{\frac{1}{2}} \frac{\theta_*}{diam (\Omega)}|x_0-P_n^i|}.\end{equation*} Hence, since x 0 is arbitrary, we conclude that there exist ![]() $C_1, C_2 \gt 0$ such that
$C_1, C_2 \gt 0$ such that
 \begin{equation*}
u_n(x)\leq C_1 e^{C_1 R}\lambda_n^{\frac{1}{p-2}}\sum_{i=1}^k e^{-C_2\lambda_n^{\frac{1}{2}}|x-P_n^i|}, ~\forall x\in A_n.
\end{equation*}
\begin{equation*}
u_n(x)\leq C_1 e^{C_1 R}\lambda_n^{\frac{1}{p-2}}\sum_{i=1}^k e^{-C_2\lambda_n^{\frac{1}{2}}|x-P_n^i|}, ~\forall x\in A_n.
\end{equation*}This completes the proof.
5. Proof of theorem 1.1
In this section, we complete the proof of theorem 1.1. We have previously established a sequence of mountain pass type critical points ![]() $\{u_{\rho_n}\}$ of
$\{u_{\rho_n}\}$ of ![]() $J_{\rho_n}$ on
$J_{\rho_n}$ on ![]() $\mathcal{S}_c$, which have uniformly bounded Morse indices. These critical points are constructed for a sequence
$\mathcal{S}_c$, which have uniformly bounded Morse indices. These critical points are constructed for a sequence ![]() $\rho_n\to 1^-$. Building on the blow-up analysis conducted in §4, we now present the following proposition.
$\rho_n\to 1^-$. Building on the blow-up analysis conducted in §4, we now present the following proposition.
Proposition 5.1. Let ![]() $\{u_n\}\subset H^1(\Omega)$ be a sequence of solutions to (4.1), corresponding to some
$\{u_n\}\subset H^1(\Omega)$ be a sequence of solutions to (4.1), corresponding to some ![]() $\{\lambda_n\}\subset \mathbb{R}$ and
$\{\lambda_n\}\subset \mathbb{R}$ and ![]() $\rho_n\to 1^-$. Suppose that
$\rho_n\to 1^-$. Suppose that
 \begin{equation*}\int_{\Omega}|u_n|^2 dx=c,~m(u_n)\leq 2,~\forall n, \end{equation*}
\begin{equation*}\int_{\Omega}|u_n|^2 dx=c,~m(u_n)\leq 2,~\forall n, \end{equation*} for some c > 0, and the energy levels ![]() $\{c_n:=J_{\rho_n}(u_n)\}$ are bounded. Then, the sequence of solution pairs
$\{c_n:=J_{\rho_n}(u_n)\}$ are bounded. Then, the sequence of solution pairs ![]() $\{(u_n, \lambda_n)\}$ is bounded in
$\{(u_n, \lambda_n)\}$ is bounded in ![]() $H^1(\Omega)\times \mathbb{R}$. Moreover,
$H^1(\Omega)\times \mathbb{R}$. Moreover, ![]() $\{u_n \}$ is a bounded Palais–Smale sequence for the functional J constrained on
$\{u_n \}$ is a bounded Palais–Smale sequence for the functional J constrained on ![]() $\mathcal{S}_c$ at level c 1.
$\mathcal{S}_c$ at level c 1.
Proof. First, we show that ![]() $\{\lambda_n\}$ is bounded. Suppose, by contradiction, that
$\{\lambda_n\}$ is bounded. Suppose, by contradiction, that ![]() $\lambda_n\to +\infty$. By lemma 4.4, there exist at most k blow-up limits
$\lambda_n\to +\infty$. By lemma 4.4, there exist at most k blow-up limits ![]() $\{P_n^1\},\ldots,\{P_n^k\}$ with
$\{P_n^1\},\ldots,\{P_n^k\}$ with ![]() $k\leq 2$ in
$k\leq 2$ in ![]() $\overline{\Omega}$.
In the following, we denote by
$\overline{\Omega}$.
In the following, we denote by ![]() $\{v_n^i \}$ the scaled sequence around
$\{v_n^i \}$ the scaled sequence around ![]() $\{P_n^i\}$, and by vi the limits of
$\{P_n^i\}$, and by vi the limits of ![]() $\{v_n^i\}$. Note that for these blow-up points
$\{v_n^i\}$. Note that for these blow-up points ![]() $\{P_n^1\},\ldots,\{P_n^k\}$, it may hold
$\{P_n^1\},\ldots,\{P_n^k\}$, it may hold
 \begin{equation*}
\lambda_n^{\frac{1}{2}}dist(P_n^i,\partial \Omega)\to +\infty ~~{\mbox or}~~\lambda_n^{\frac{1}{2}}dist(P_n^i,\partial \Omega)\to d\geq 0.
\end{equation*}
\begin{equation*}
\lambda_n^{\frac{1}{2}}dist(P_n^i,\partial \Omega)\to +\infty ~~{\mbox or}~~\lambda_n^{\frac{1}{2}}dist(P_n^i,\partial \Omega)\to d\geq 0.
\end{equation*} Without loss of generality, assume there exists an integer ![]() $k_1\in \{0, 1,\ldots, k\}$ such that
$k_1\in \{0, 1,\ldots, k\}$ such that
 \begin{eqnarray*}
\lambda_n^{\frac{1}{2}}dist(P_n^i,\partial \Omega)\to +\infty~~ \mbox{for every}~~ i\in \{1,\ldots, k_1\},
\end{eqnarray*}
\begin{eqnarray*}
\lambda_n^{\frac{1}{2}}dist(P_n^i,\partial \Omega)\to +\infty~~ \mbox{for every}~~ i\in \{1,\ldots, k_1\},
\end{eqnarray*}and
 \begin{eqnarray*}
\lambda_n^{\frac{1}{2}}dist(P_n^j,\partial \Omega)\to d\geq 0~~ \mbox{for every}~~ j\in \{k_1+1,\ldots, k\}.
\end{eqnarray*}
\begin{eqnarray*}
\lambda_n^{\frac{1}{2}}dist(P_n^j,\partial \Omega)\to d\geq 0~~ \mbox{for every}~~ j\in \{k_1+1,\ldots, k\}.
\end{eqnarray*}On the one hand, we can deduce that for any R > 0,
 \begin{equation}
\bigg| \lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega}u_n^2 dx-\sum_{i=1}^{k_1}\int_{B_R(0)}|v_n^i|^2 dx-\sum_{i=k_1+1}^{k}\int_{B_R(0)\cap {\Omega}_n}|v_n^i|^2 dx \bigg|\to +\infty.
\end{equation}
\begin{equation}
\bigg| \lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega}u_n^2 dx-\sum_{i=1}^{k_1}\int_{B_R(0)}|v_n^i|^2 dx-\sum_{i=k_1+1}^{k}\int_{B_R(0)\cap {\Omega}_n}|v_n^i|^2 dx \bigg|\to +\infty.
\end{equation} In fact, since ![]() $p\in (2_*, 2^*)$, the first term satisfies
$p\in (2_*, 2^*)$, the first term satisfies
 \begin{equation*}
\bigg| \lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega}u_n^2 dx \bigg|=\lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}c\to +\infty.
\end{equation*}
\begin{equation*}
\bigg| \lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega}u_n^2 dx \bigg|=\lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}c\to +\infty.
\end{equation*}By lemma 4.4, we have
 \begin{equation*}
\sum_{i=1}^{k_1}\int_{B_R(0)}|v_n^i|^2 dx\to \sum_{i=1}^k \int_{B_R(0)} |v^i|^2 dx,
\end{equation*}
\begin{equation*}
\sum_{i=1}^{k_1}\int_{B_R(0)}|v_n^i|^2 dx\to \sum_{i=1}^k \int_{B_R(0)} |v^i|^2 dx,
\end{equation*}and
 \begin{equation*}
\sum_{i=k_1+1}^{k}\int_{B_R(0)\cap \overline{\Omega}_n}|v_n^i|^2 dx\to \sum_{i=1}^k \int_{B_R(0)\cap \mathbb{R}_+^N} |v^i|^2 dx,
\end{equation*}
\begin{equation*}
\sum_{i=k_1+1}^{k}\int_{B_R(0)\cap \overline{\Omega}_n}|v_n^i|^2 dx\to \sum_{i=1}^k \int_{B_R(0)\cap \mathbb{R}_+^N} |v^i|^2 dx,
\end{equation*}which imply that (5.1) holds.
On the other hand, by lemma 4.5, there exist constants ![]() $C, C' \gt 0$ such that
$C, C' \gt 0$ such that
 \begin{eqnarray*}
\begin{aligned}
&\bigg| \lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega}u_n^2 dx
-\sum_{i=1}^{k_1}\int_{B_R(0)}|v_n^i|^2 dx-\sum_{i=k_1+1}^{k}\int_{B_R(0)\cap {\Omega}_n}|v_n^i|^2 dx \bigg|\\
&= \lambda_n^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega\backslash \cup_{i=1}^{k} (B_{R\lambda_n^{-1/2}}(P_n^i)\cap \Omega)}u_n^2 dx\\
&\leq C_1 e^{2C_1 R}\lambda_n^{\frac{N}{2}}\sum_{i=1}^{k}\int_{\mathbb{R}^N\backslash \cup_{i=1}^{k}B_{R\lambda_n^{-1/2}}(P_n^i)}e^{-2C_2\lambda_n^{\frac{1}{2}}|x-P_n^i|} dx\\
&\leq C e^{C R}\sum_{i=1}^{k}\int_{\mathbb{R}^N\backslash B_R(0)} e^{-2C_2|y|} dy \leq C'=C'(R).
\end{aligned}
\end{eqnarray*}
\begin{eqnarray*}
\begin{aligned}
&\bigg| \lambda_n ^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega}u_n^2 dx
-\sum_{i=1}^{k_1}\int_{B_R(0)}|v_n^i|^2 dx-\sum_{i=k_1+1}^{k}\int_{B_R(0)\cap {\Omega}_n}|v_n^i|^2 dx \bigg|\\
&= \lambda_n^{\frac{N}{2}-\frac{2}{p-2}}\int_{\Omega\backslash \cup_{i=1}^{k} (B_{R\lambda_n^{-1/2}}(P_n^i)\cap \Omega)}u_n^2 dx\\
&\leq C_1 e^{2C_1 R}\lambda_n^{\frac{N}{2}}\sum_{i=1}^{k}\int_{\mathbb{R}^N\backslash \cup_{i=1}^{k}B_{R\lambda_n^{-1/2}}(P_n^i)}e^{-2C_2\lambda_n^{\frac{1}{2}}|x-P_n^i|} dx\\
&\leq C e^{C R}\sum_{i=1}^{k}\int_{\mathbb{R}^N\backslash B_R(0)} e^{-2C_2|y|} dy \leq C'=C'(R).
\end{aligned}
\end{eqnarray*} Taking ![]() $n\to +\infty$, we obtain a contradiction to (5.1).
Hence,
$n\to +\infty$, we obtain a contradiction to (5.1).
Hence, ![]() $\{\lambda_n\}$ is bounded.
$\{\lambda_n\}$ is bounded.
Now, we show that ![]() $\{u_n\}$ is bounded in
$\{u_n\}$ is bounded in ![]() $H^1(\Omega)$. By contradiction, we suppose that
$H^1(\Omega)$. By contradiction, we suppose that ![]() $\|u_n\|\to \infty$. Using standard arguments, we have
$\|u_n\|\to \infty$. Using standard arguments, we have ![]() $\|u_n\|_{L^\infty} \to \infty.$ Take
$\|u_n\|_{L^\infty} \to \infty.$ Take ![]() $P_n\in \overline{\Omega}$ such that
$P_n\in \overline{\Omega}$ such that ![]() $|u_n(P_n)|=\|u_n\|_{L^{\infty}}$. Let
$|u_n(P_n)|=\|u_n\|_{L^{\infty}}$. Let  $\tilde{\epsilon}_n=a_0^{-\frac{1}{2}}|u_n(P_n)|^{-\frac{p-2}{2}}$ and define
$\tilde{\epsilon}_n=a_0^{-\frac{1}{2}}|u_n(P_n)|^{-\frac{p-2}{2}}$ and define
 \begin{equation*}
\tilde{u}_n(x):=a_0^{\frac{1}{p-2}}\tilde{\epsilon}_n^{\frac{2}{p-2}}u_n(\tilde{\epsilon}_nx+ P_n)~~{\rm for}~~ x\in \tilde{\Omega}_n:=\frac{\Omega-P_n}{\tilde{\epsilon}_n}.
\end{equation*}
\begin{equation*}
\tilde{u}_n(x):=a_0^{\frac{1}{p-2}}\tilde{\epsilon}_n^{\frac{2}{p-2}}u_n(\tilde{\epsilon}_nx+ P_n)~~{\rm for}~~ x\in \tilde{\Omega}_n:=\frac{\Omega-P_n}{\tilde{\epsilon}_n}.
\end{equation*} Clearly, ![]() $\tilde{u}_n$ satisfies (4.8). Using the boundedness of
$\tilde{u}_n$ satisfies (4.8). Using the boundedness of ![]() $\{\lambda_n\}$, we get
$\{\lambda_n\}$, we get ![]() $\lambda_n \tilde{\epsilon}_n^2 \to 0$ as
$\lambda_n \tilde{\epsilon}_n^2 \to 0$ as ![]() $n\to \infty$. Then, up to a subsequence,
$n\to \infty$. Then, up to a subsequence, ![]() $\tilde{u}_n\to \tilde{u}$ in
$\tilde{u}_n\to \tilde{u}$ in ![]() $C^2_{loc}(\overline{D})$, where
$C^2_{loc}(\overline{D})$, where ![]() $\tilde{u}$ is a finite Morse index solution of
$\tilde{u}$ is a finite Morse index solution of
 \begin{equation}
\left\{\begin{array}{ll}
-\Delta \tilde{u} =|\tilde{u}|^{p-2}\tilde{u} & {\mathrm{in}} \,~ D,\\
|\tilde{u}(x)|\leq |\tilde{u}(0)|=1 & {\mathrm{in}} \,~ D, \\
\frac{\partial \tilde{u}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D,
\end{array}\right.
\end{equation}
\begin{equation}
\left\{\begin{array}{ll}
-\Delta \tilde{u} =|\tilde{u}|^{p-2}\tilde{u} & {\mathrm{in}} \,~ D,\\
|\tilde{u}(x)|\leq |\tilde{u}(0)|=1 & {\mathrm{in}} \,~ D, \\
\frac{\partial \tilde{u}}{\partial \nu}=0 \, &{\mathrm{on}}\,~\partial D,
\end{array}\right.
\end{equation} where D is either ![]() $\mathbb{R}^N$ or a half space. By invoking [Reference Farina22, theorem 2] and [Reference Yu57, proposition 2.1], respectively, we conclude that
$\mathbb{R}^N$ or a half space. By invoking [Reference Farina22, theorem 2] and [Reference Yu57, proposition 2.1], respectively, we conclude that ![]() $\tilde{u}\equiv 0$. This contradicts to the fact that
$\tilde{u}\equiv 0$. This contradicts to the fact that ![]() $|\tilde{u}(0)|=1$. Therefore, we deduce that
$|\tilde{u}(0)|=1$. Therefore, we deduce that ![]() $\{u_n\}$ is a bounded sequence in
$\{u_n\}$ is a bounded sequence in ![]() $H^1(\Omega)$. Consequently, employing standard arguments, we establish that
$H^1(\Omega)$. Consequently, employing standard arguments, we establish that ![]() $\{u_n \}$ is a bounded Palais–Smale sequence for
$\{u_n \}$ is a bounded Palais–Smale sequence for ![]() $J|_{\mathcal{S}_c}$ at level c 1.
$J|_{\mathcal{S}_c}$ at level c 1.
Completion of proof of theorem 1.1
Let ![]() $\{u_n\}$ be the sequence given in proposition 5.1 for some
$\{u_n\}$ be the sequence given in proposition 5.1 for some ![]() $c\in (0, c^*)$. By the compact embedding
$c\in (0, c^*)$. By the compact embedding ![]() $H^1(\Omega)\hookrightarrow L^r(\Omega)$ for
$H^1(\Omega)\hookrightarrow L^r(\Omega)$ for ![]() $r\in [1,2^*)$, and using similar arguments as in §3, we can deduce that
$r\in [1,2^*)$, and using similar arguments as in §3, we can deduce that ![]() $u_{n}\to u$ strongly in
$u_{n}\to u$ strongly in ![]() $H^1(\Omega)$. This, in turn, implies that u is a mountain pass type normalized solution of (1.1).
$H^1(\Omega)$. This, in turn, implies that u is a mountain pass type normalized solution of (1.1).
Acknowledgements
Xiaojun Chang was partially supported by NSFC (12471102) and the Research Project of the Education Department of Jilin Province (JJKH20250296KJ). The research of V.D. Rădulescu was supported by the grant ‘Nonlinear Differential Systems in Applied Sciences’ of the Romanian Ministry of Research, Innovation and Digitization, within PNRR-III-C9-2022-I8/22.