Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-30T01:12:32.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-existence theorems for quasilinear elliptic equations with weights

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  28 April 2025

Roberta Filippucci Open the ORCID record for Roberta Filippucci [Opens in a new window]  and
Yadong Zheng
Roberta Filippucci*
Affiliation:
Dipartimento di Matematica e Informatica, Università degli Studi di Perugia, Perugia, 06123, Italy ([email protected]) (corresponding author)
Yadong Zheng
Affiliation:
School of Mathematical Sciences and LPMC, Nankai University, Tianjin, 300071, China ([email protected])
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we deal with non-existence results, i.e., Liouville type results, for positive radial solutions of quasilinear elliptic equations with weights both in the entire 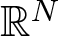$\mathbb R^N$ and in a ball, in the latter case under Dirichlet boundary conditions. The presence of weights, possibly singular or degenerate, makes the study fairly delicate. The proofs use a Pohozaev type identity combined with an accurate qualitative analysis of solutions. In the last part of the article, a non-existence theorem is proved for a Dirichlet problem with a convection term.

Keywords

generalized mean curvature operatorLiouville type theoremspositive radial solutionsquasilinear elliptic equationsweight functions

MSC classification

Primary: 35J62: Quasilinear elliptic equations 35B33: Critical exponents
Secondary: 35A24: Methods of ordinary differential equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 33
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alarcón, S., Garcia-Melian, J. and Quaas, A.. Existence and non-existence of solutions to elliptic equations with a general convection term. Proc. Roy. Soc. Edinburgh Sect. A 144 (2014), 225–239.CrossRefGoogle Scholar
Aubin, T.. Problèmes isopérimétriques et espaces de Sobolev. J. Differ. Geom. 11 (1976), 573–598.CrossRefGoogle Scholar
Azzollini, A.. Ground state solutions for the Hénon prescribed mean curvature equation. Adv. Nonlinear Anal. 8 (2019), 1227–1234.CrossRefGoogle Scholar
Baldelli, L., Brizi, V. and Filippucci, R.. Existence and nonexistence of positive radial solutions of a quasilinear Dirichlet problem with diffusion. J. Differential Equations 359 (2023), 107–151.CrossRefGoogle Scholar
Brezis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
Caristi, G. and Mitidieri, E.. Nonexistence of positive solutions of quasilinear equations. Adv. Differ. Equ. 2 (1997), 319–359.Google Scholar
Clément, P., Manásevich, R. and Mitidieri, E.. On a modified capillary equation. J. Diff. Equations 124 (1996), 343–358.CrossRefGoogle Scholar
Clément, P., Manásevich, R. and Mitidieri, E.. Some existence and non-existence results for a homogeneous quasilinear problem. Asymptot. Anal. 17 (1998), 13–29.Google Scholar
Clement, P., de Figueiredo, D. G. and Mitidieri, E.. Quasilinear elliptic equations with critical exponents. Topol. Methods Nonlinear Anal. 7 (1996), 133–170.CrossRefGoogle Scholar
Corsato, C., De Coster, C., Flora, N. and Omari, P.. Radial solutions of the Dirichlet problem for a class of quasilinear elliptic equations arising in optometry. Nonlinear Anal. 181 (2019), 9–23.CrossRefGoogle Scholar
Del Pino, M. and Guerra, I.. Ground states of a prescribed mean curvature equation. J. Diff. Equations 241 (2007), 112–129.CrossRefGoogle Scholar
Deuel, J. and Hess, P.. A criterion for the existence of solutions of non-linear elliptic boundary value problems. Proc. Roy. Soc. Edinburgh Sect. A 74 (1976), 49–54.CrossRefGoogle Scholar
Egnell, H.. Elliptic boundary value problems with singular coefficients and critical nonlinearities. Indiana Univ. Math. J. 38 (1989), 235–551.CrossRefGoogle Scholar
Filippucci, R. and Zheng, Y.. Existence and nonexistence of solutions for the mean curvature equation with weights. Math. Ann. 390 (2024), 5821–5861.CrossRefGoogle Scholar
Ghergu, M. and Radulescu, V.. Existence and nonexistence of entire solutions to the logistic differential equation. Abstr. Appl. Anal. 17 (2003), 995–1003.CrossRefGoogle Scholar
Gidas, B. and Spruck, J.. A priori bounds for positive solutions of nonlinear elliptic equations. Commun. Partial Differ. Equ. 6 (1981), 883–901.CrossRefGoogle Scholar
Liskevich, V., Lyakhova, S. and Moroz, V.. Positive solutions to singular semilinear elliptic equations with critical potential on cone-like domains. Adv. Differential Equations 11 (2006), 361–398.CrossRefGoogle Scholar
Mitidieri, E. and Pohozaev, S. I.. Nonexistence of positive solutions for a system of quasilinear elliptic equations and inequalities in $\mathbb{R}^N$. Dokl. Math. 59 (1999), 351–355.Google Scholar
Mitidieri, E., Sweers, G. and van der Vorst, R.. Non-existence theorems for systems of quasilinear partial, differential equations. Differential Integral Equations 8 (1995), 1331–1354.CrossRefGoogle Scholar
Ni, W.-M. and Serrin, J.. Existence and non-existence theorems for ground states for quasilinear partial differential equations. Atti Convegni Lincei. 77 (1985), 231–257.Google Scholar
Ni, W.-M. and Serrin, J.. Non-existence theorems for quasilinear partial differential equations. Rend. Circ. Mat. Palermo Suppl. 8 (1985), 171–185.Google Scholar
Ni, W.-M. and Serrin, J.. Nonexistence theorems for singular solutions of quasilinear partial differential equations. Comm. Pure Appl. Math. 39 (1986), 379–399.CrossRefGoogle Scholar
Serrin, J.. Positive solutions of a prescribed mean curvature problem, calculus of variations and partial differential equations, Lecture Notes in Mathematics, (Springer, Berlin, 1340, 1988).Google Scholar
Serrin, J. and Zou, H.. Cauchy-Liouville and universal boundedness theorems for quasilinear elliptic equations and inequalities. Acta Math. 189 (2002), 79–142.CrossRefGoogle Scholar
Trudinger, N.. Remarks concerning the conformal deformation of Riemannian structures on compact manifolds. Ann. Sc. Norm. Super. Pisa, Cl. Sci. 22 (1968), 265–274.Google Scholar