Both the reflection and transmission coefficients of oil palm fruits of various moisture contents have been measured using a rectangular dielectric waveguide (RDWG) technique in the frequency range between 8 GHz and 12 GHz. Good agreement between predicted and measured values of reflection coefficient suggests the potential of RDWG technique as a new, fast and accurate method for the determination of moisture content in oil palm fruits.

Literature shows a lack of works based on non-invasive methods for computing the propagation coefficient γ, a complex number related to dynamic vascular properties. Its imaginary part is inversely related to the wave speed C through the relationship $C=\omega/{\rm Im}(\gamma)$ 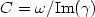, while its real part a, called attenuation, represents loss of pulse energy per unit of length. In this work an expression is derived giving the propagation coefficient when assuming a pulsatile flow through a viscoelastic vessel. The effects of physical and geometrical parameters of the tube are then studied. In particular, the effects of increasing the reflection coefficient, on the determination of the propagation coefficient are investigated in a first step. In a second step, we simulate a variation of tube length under physiological conditions. The method developed here is based on the knowledge of instantaneous velocity and radius values at only two sites. It takes into account the presence of a reflection site of unknown reflection coefficient, localised in the distal end of the vessel. The values of wave speed and attenuation obtained with this method are in a good agreement with the theory. This method has the advantage to be usable for small portions of the arterial tree.

A comprehensive integrated model of stochastic convective transport in a solidifying binary melt is presented in this work. The detailed transport phenomena in the particle and bulk phases are coupled together through a stochastic Eulerian-Lagrangian formalism, capturing the physical mechanisms and consequences of particle agglomeration, de-agglomeration, and the underlying hydrodynamic interactions. The interactions between random thermo-fluidic fluctuations in the continuum carrier phase and the associated growth/dissolution of particle phases are modeled by employing a Langevin formalism. Representative case studies highlighting the implications of the dynamics of the fragmented dendrites on the overall convective patterns in an electromagnetically-stirred semi-solid binary melt are subsequently presented, so as to emphasize on the comprehensive physical bases and to illustrate the fundamental approach of the present predictive methodology.