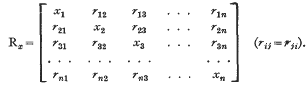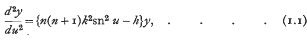Proceedings of the Royal Society of Edinburgh, Volume 60 - 1940
- This volume was published under a former title. See this journal's title history.
Proceedings
The Design and Interpretation of Experiments based on a Four-fold Table : the Statistical Assessment of the Effect of Treatment
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 362-375
-
- Article
- Export citation
X.—Interpolated Derivatives
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 134-140
-
- Article
- Export citation
XIX.—The Effect of the Inhibition of Respiration and Assimilation on the Diatom Ditylum Brightwelli (West)
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 245-259
-
- Article
- Export citation
I.—On a Problem concerning Matrices with Variable Diagonal Elements
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 1-17
-
- Article
- Export citation
XX.—The Structure and Behaviour of the Chromosomes of the Sheep during Mitosis and Meiosis
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 260-270
-
- Article
- Export citation
II.—The Maximal Range of Error in Gross Reproduction Rates
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 18-32
-
- Article
- Export citation
Obituary Notices
Charles Eugène Barrois, For. Mem. R.S., Hon. F.R.S.E.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 376-378
-
- Article
-
- You have access
- Export citation
Proceedings
XI.—Reciprocity. Part III: Reciprocal Wave Functions
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 141-146
-
- Article
- Export citation
XII.—Reciprocity. Part IV: Spinor Wave Functions
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 147-163
-
- Article
- Export citation
III.—Observations on the Œstrous Cycle of the Guinea-Pig
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 33-39
-
- Article
- Export citation
Obituary Notices
Sir Thomas Hudson Beare, B.A., B.Sc., LL.D., M.Inst.C.E., M.I.Mech.E.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 379-381
-
- Article
-
- You have access
- Export citation
Proceedings
XXI.—The Swimming and Burrowing Habits of the Amphipod Urothoë marina (Bate)
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 271-280
-
- Article
- Export citation
XIII.—Tests of Carcinogenic Substances in Relation to the Production of Mutations in Drosophila melanogaster
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 164-173
-
- Article
- Export citation
Obituary Notices
Sir George Andreas Berry, LL.D., F.R.C.S.E.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 382-384
-
- Article
-
- You have access
- Export citation
Proceedings
XXII.—Random Paths in Two and Three Dimensions
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 281-298
-
- Article
- Export citation
IV.—On the Independence of Linear and Quadratic Forms in Samples of Normally Distributed Variates
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 40-46
-
- Article
- Export citation
Obituary Notices
Waldemar Christofer Brøgger, For. Mem. R.S., Hon. F.R.S.E.
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 385-386
-
- Article
-
- You have access
- Export citation
Proceedings
XXIII.—An Analysis of the Influence of Weather upon a Migratory Movement of Birds
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 299-321
-
- Article
- Export citation
V.—The Periodic Lamé Functions
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 47-63
-
- Article
- Export citation
XIV.—The Genetical and Mechanical Properties of the Sex Chromosome. VI. Hexacentrus mundus
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 174-181
-
- Article
- Export citation