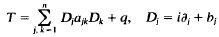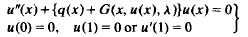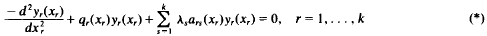Research Article
Dirichlet and separation results for Schrödinger-type operators
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 151-162
-
- Article
- Export citation
A boundary-value problem for an ordinary differential equation whose coefficients are in a B*-algebra
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 323-332
-
- Article
- Export citation
Related oscillation criteria for higher order self-adjoint differential and integro-differential equations§
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 333-345
-
- Article
- Export citation
Über das Verhalten der Lösung des Dirichletproblems am Rand des Gebietes, wenn der Rand zur Klasse C2α gehört
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 163-176
-
- Article
- Export citation
Non-linear Sturm-Liouville problems with no secondary bifurcation†
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 347-356
-
- Article
- Export citation
Front matter
PRM volume 80 issue 1-2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 80 issue 1-2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
The interlacing of eigenvalues for periodic multi-parameter problems*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 357-362
-
- Article
- Export citation
Index
Index
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 363-365
-
- Article
- Export citation
Front matter
PRM volume 80 issue 3-4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 80 issue 3-4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b7
-
- Article
-
- You have access
- Export citation