Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:28:24.832Z Has data issue: false hasContentIssue false
  • English
  • Français

The interlacing of eigenvalues for periodic multi-parameter problems*

Published online by Cambridge University Press:  14 November 2011

Patrick J. Browne
Patrick J. Browne
Affiliation:
University of Calgary, Calgary, Alberta, Canada
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper studies a linked system of second order ordinary differential equations

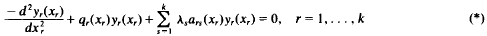
where xx ∈ [ar, br] and the coefficients qrars are continuous, real valued and periodic of period (br − ar), 1 ≤ r,s ≤ k. We assume the definiteness condition det{ars(xr)} > 0 and 2k possible multiparameter eigenvalue problems are then formulated according as periodic or semi-periodic boundary conditions are imposed on each of the equations of (*). The main result describes the interlacing of the 2k possible sets of eigentuples thus extending to the multiparameter case the well known theorem concerning 1-parameter periodic equation.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 80 , Issue 3-4 , 1978 , pp. 357 - 362
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Binding, P. A. and Browne, P. J. A Variational Approach to multiparameter Eigenvalue Problems in Hilbert Space. S.I.A.M. J. Math. Anal., to appear.Google Scholar
2Eastham, M. S. P.The Spectral Theory of Periodic Differential Equations (Edinburgh: Scottish Academic Press, 1973).Google Scholar
3Weinstein, A. and Stenger, W.Methods of Intermediate Problems for Eigenvalues (New York: Academic Press, 1972).Google Scholar