The Hopf algebra structure of H*(ΩG, F2) and the action of the dual Steenrod algebra are completely and explicitly determined when G isone of the connected, simply connected, exceptional, simple Lie groups. The approach is homological, using connected coverings and spectral sequences.

In this paper we prove that the domain of hyperbolicity of the polynomial xn + λ2nn−2+λ3xn−3+ … + λn,λiϵR intersected by the half-space λ2 ≧ – 1, has the property of Whitney, i.e., every two points of this set can be connected by a piecewise-smooth curve belonging to it, whose length is ≦C times greater than the euclidian distance between the points, where the constant C does not depend on the choice of the points. Parallel with this, we show that the values x1≦x2≦…≦xn of a random variable are uniquely determined by the corresponding probabilities and by thefirst n moments.

The theory of subordinacy is extended to all one-dimensional Schrödinger operatorsfor which the corresponding differential expression L = – d2/(dr2) + V(r) is in the limit point case at both ends of an interval (a, b), with V(r) locally integrable. This enables a detailed classification of the absolutely continuous and singular spectra to be established in terms of the relative asymptotic behaviour of solutions of Lu = xu, x εℝ, as r→a and r→b. The result provides a rigorous but straightforward method of direct spectral analysis which has very general application, and somefurther properties of the spectrum are deduced from the underlying theory.

Let G and G' be two connected compact Lie groups with maximal tori T and T'. For a space X, let Xp be the p-completion of X. We will associate to each topological map f:(BG)p→(BG')p an “admissible map” ϕ:π1(T)⊗zZp→π1(T′)⊗zZp. We then show that the study of “admissible maps” in the p-complete case may be reduced to their study in the p-local case.

In this paper, a theory of fractional powers of operators due to Balakrishnan, which is valid for certain operators on Banach spaces, is extended to Fréchet spaces. The resultingtheory is shown to be more general than that developed in an earlier approach by Lamb, and is applied to obtain mapping properties of certain Riesz fractional integral operators on spaces of test functions.

A new proof is given of the partial regularity of minimisers under the principal assumptions of uniform strict quasiconvexity and polynomial growth. The proof is based on a Caccioppoli inequality and an “indirect” blow-up argument; this avoids the technical complications of a “direct” argument.

We prove a lower bound for the Dirichlet heat kernel pD(x,y;t), where x and y are a visible pair of points in an open set D in ℝm.

We show that the property of linear operators to be in the surjective hull (injective hull) of the ideal of strictly singular (strictly cosingular) operators between Banach spaces is an interpolation property with respect to the real interpolation method with parameters 0 < ủ < 1 and < p < ℞.

We prove that for every dense Gδ set H, there exists a continuous function f, such that f intersects every analytic function in finitely many points and f is infinitely differentiable exactly at the points of H. This answers a problem of S. Agronsky, A. M. Bruckner, M. Laczkovich and D. Preiss. They proved a result which implies that every continuous function with finite intersections with analytic functions is infinitely differentiable at the points of a dense Gδ set.

In this paper we study the equilibrium equations for axisymmetric deformations of isotropic circular plates in tension. We give results on the global multiplicity of solutions and study the stability of the trivial homogeneous solution for large displacements.

The dynamics of a population inhabiting a strongly heterogeneous environment are modelledby diffusive logistic equations of the form ut = d Δu + [m(x) — cu]u in Ω × (0, ∞), where u represents the population density, c, d > 0 are constants describing the limiting effects of crowding and the diffusion rate of the population, respectively, and m(x) describes the local growth rate of the population. If the environment ∞ is bounded and is surrounded by uninhabitable regions, then u = 0 on ∂∞× (0, ∞). The growth rate m(x) is positive on favourablehabitats and negative on unfavourable ones. The object of the analysis is to determine how the spatial arrangement of favourable and unfavourable habitats affects the population being modelled. The models are shown to possess a unique, stable, positive steady state (implying persistence for the population) provided l/d> 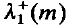where 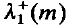is the principle positive eigenvalue for the problem — Δϕ=λm(x)ϕ in Χ,ϕ=0 on ∂Ω. Analysis of how 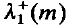depends on m indicates that environments with favourable and unfavourable habitats closely intermingled are worse for the population than those containing large regions of uniformly favourable habitat. In the limit as the diffusion rate d ↓ 0, the solutions tend toward the positive part of m(x)/c, and if m is discontinuous develop interior transition layers. The analysis uses bifurcation and continuation methods, the variational characterisation of eigenvalues, upper and lower solution techniques, and singular perturbation theory.

A method of Jensen is extended to show that the second derivatives of the solutions of various linear obstacle problems are bounded under weaker regularity hypotheses on the dataof the problem than were allowed by Jensen. They are, in fact, weak enough that the linear results imply the boundedness of the second derivatives for quasilinear problems as well. Comparisons are made with previously known results, some of which are proved by similar methods. Both Dirichlet and oblique derivative boundary conditions are considered. Corresponding results for parabolic obstacle problems are proved.

Depending upon the initial data associated with the fundamental matrix, the function M(λ), used to generate L2-solutions of homogeneous linear differential systems, may vary. We show that there is a matrix bilinear transformation between such functions M(λ) with different initial data and illustrate how the result can be used to simplify the calculation of a specific M(λ)-function for a scalar second-order problem.

Let then, for certain weight functions u and v and indices p,q, it is shown that ∥Tαf∥q, u≦C∥grad f ∥p, v'q > n / α holds. For α=l,p=q and u = v ≡ l this reduces to a result of M. Weiss. In addition we establish n-dimensional weighted Hardy—Littlewood type inequalities ofthe form for large classes of weights.

An Lp inequality for l < p < 2 is established and applications to fixed points of uniformly Lipschitz mappings and strongly unique best approximations are given.