Research Article
Low energy resolvent estimates and continuity of time-delay operators
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 229-242
-
- Article
- Export citation
A Laplace transform relevant to holomorphic semigroups
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 243-258
-
- Article
- Export citation
Conjugacy classes in finite groups
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 259-264
-
- Article
- Export citation
On a new class of Hardy type inequalities
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 265-274
-
- Article
- Export citation
Radial entire solutions to even order semilinear elliptic equations in the plane
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 275-287
-
- Article
- Export citation
Global existence and convergence to a singular steady state for a semilinear heat equation
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 289-305
-
- Article
- Export citation
U-algebras and the Hahn–Banach extension theorem*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 307-317
-
- Article
- Export citation
Conformal maps in methods of asymptotic continuation
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 319-335
-
- Article
- Export citation
Sturmian theory for nonself-adjoint differential equations of second order
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 337-343
-
- Article
- Export citation
An elementary proof of Gorny's inequality
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 345-349
-
- Article
- Export citation
Index
Index to Volume 105
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. v-vi
-
- Article
- Export citation
Front matter
PRM volume 105 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 105 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation

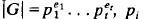 , prime and
, prime and 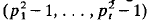 . The above congruence is obtained without using character theory. We also obtain new local congruences that slightly improve Mann's congruence.
. The above congruence is obtained without using character theory. We also obtain new local congruences that slightly improve Mann's congruence.
