Research Article
Existence and stability of travelling wave solutions for an evolutionary ecology model
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-18
-
- Article
- Export citation
On blow-up and degeneracy for the semilinear heat equation with source
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 19-24
-
- Article
- Export citation
On the topological properties of symplectic maps
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 25-38
-
- Article
- Export citation
Stability of discontinuous steady states in shearing motions of a non-Newtonian fluid
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 39-59
-
- Article
- Export citation
Compact attractor for a nonlinear wave equation with critical exponent
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 61-64
-
- Article
- Export citation
On the asymptotic decay of L2-solutions of one-body Schrödinger equations in unbounded domains*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 65-86
-
- Article
- Export citation
Corrigendum: Spectral properties of two parameter eigenvalue problems II
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 87-90
-
- Article
- Export citation
Nonlinear analytic semiflows*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 91-107
-
- Article
- Export citation
On contracted semigroup rings
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 109-117
-
- Article
- Export citation
A factorisation procedure for two by two matrix functions on the circle with two rationally independent entries
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 119-138
-
- Article
- Export citation
A variational approach to a nonlinear Steklov problem
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 139-149
-
- Article
- Export citation
On the Gegenbauer transformation
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 151-166
-
- Article
- Export citation
Complicated dynamics of scalar reaction diffusion equations with a nonlocal term
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 167-192
-
- Article
- Export citation
Front matter
PRM volume 115 issue 1-2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 115 issue 1-2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation

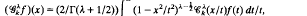
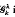 being the Gegenbauer polynomial of index λ and degree
being the Gegenbauer polynomial of index λ and degree